基于自适应无迹卡尔曼滤波算法的月壤参数估计

王志福， 王学晨， 王 阳， 梁常春， 王 瑞

（1.北京理工大学电动车辆国家工程研究中心，北京 100081；2.空间智能机器人系统技术与应用北京市重点实验室，北京空间飞行器总体设计部，北京 100094）

0 引言

载人月球探测技术既是无人探月技术发展的延续，又是建造月球基地目标实现的基础，标志着月球探测开始进入长期发展阶段［1-2］。作为载人月球探测中不可或缺的角色，载人月球车是宇航员能在月面顺利完成各项探测任务的保证。月球表面地形信息对载人月球车而言是十分重要的，尤其是获取准确的月壤参数信息在很大程度上影响着月球车的行驶性能。对月壤参数的准确估计，有利于后续对月球车行驶过程中运动状态量进行控制，进一步优化月球车行驶能力，提高月球车操纵稳定性，也能为未来探月技术研究发展奠定基础。

Shibly等［3］对轮壤模型进行简化，并对土壤内聚力和内摩擦角进行了估计。Kang［4］为解决深空探测星球土壤力学参数无法直接测量的难题，设计基于车轮沉陷量的土壤参数估计方法，基于视觉估计车轮沉陷量并进行处理，采集车轮信息，利用应用统计方法对月壤参数进行反演。Xue等［5］基于车轮信息设计采用最小二乘法的月壤参数识别模型，能对在轨月球车月壤力学参数进行估计，该方法需要对数据进行预处理。崔平远等［6］通过Guass-Legendre 数值积分和Newton迭代对轮壤模型进行简化，在线估计月壤参数。Ding等［7］建立轮壤解耦模型，通过最小二乘法预测月壤参数，但只在低滑转率时有效。

本文设计月壤参数估计器，对月壤力学参数的识别首先对轮壤相互作用模型进行简化，基于自适应无迹卡尔曼滤波算法对月壤参数进行识别。设置不同工况对设计的估计器效果进行了验证。

1 月球车轮壤模型

Bernstein［8］以车轮沉陷作为出发点，得出车轮压力和土壤沉陷量之间的关系。Bekker［9］在Bernstein研究的基础上总结出Bekker 应力模型。Janosi［10］与Bekker正应力模型为后续研究工作奠定了理论基础。Reece等［11］对Bekker正应力模型进行了修正，增加了最大应力角、进入角和离去角等参数，对正应力分布公式进行了完善。这些应力分布理论为后续研究人员对星球车轮壤作用力学的研究提供了基础，并且还在不断完善修正。

在松软月面，车轮行驶过程中会使月壤压缩变形，根据Bekker半经验法思想，轮壤之间的相互作用导致月壤发生变形可分为相互独立的法向变形和切向变形，也即车轮对月壤的承压特性和剪切特性，如图1所示。

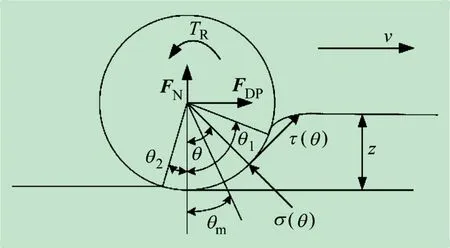
图1 轮壤应力分布

根据Bekker 提出的正应力模型，车轮-月壤作用面的平均正压力

式中：kc为内聚力变形模量；b为压板半径；kφ为摩擦变形模量；z为压板沉陷量；n为沉陷指数。

根据车轮沉陷模型，车轮在月壤上的静态沉陷量

式中：W为车轮载荷；D为车轮直径。

当车轮在滑转时，沉陷量会有所增加，Bekker 认为滑转沉陷量是关于滑移率的线性函数，因此车轮的总沉陷量

式中：hb为轮刺高度；s为车轮滑移率。

根据Janosi剪切应力模型，车轮下方的剪切应力τ与剪切变形j关系

式中：τmax＝（c+σtan φ）为最大剪切应力，其中，c为月壤内聚力；φ为内摩擦角；j0为切变模量。

根据车轮几何关系，可得到沉陷量z和车轮进入角θ1之间关系

式中，R为车轮半径。剪切变形

式中，θ为轮壤接触区域角度。

车轮在实际行驶过程中，会发生滑转，导致车轮的正压力分布峰值并不在其正下方，而会产生角度的偏移

式中，c1和c2为最大应力角系数。

根据Wong-Reece的修正正应力分布模型，车轮正下方的正应力分布和剪切应力分布可分别为：

式中，θ2为车轮离去角。

车轮的垂直载荷FN、挂钩牵引力FDP和月壤力矩TR分别为：

由式（10）～（12）构成的载人月球车轮壤相互作用模型以复杂的积分表示，很难用于求解月壤参数识别，要对轮壤作用应力-应变分布模型进行简化，将轮地作用力进行线性化［3，12］。

令：

式中，E＝1 -exp｛-R［（θ1-θm）-（1 -s）（sin θ1-sin θm）］／j0｝。则式（8）正应力分布和式（9）剪切应力分布可分别简化为：

对积分式求解并进行简化，可得车轮垂向载荷FN、月壤力矩TR和挂钩牵引力FDP表达式分别为：

式中，B＝。

由表达式可得，若要通过轮壤相互作用关系求解车轮力，还需要计算出各车轮的滑移率。

车轮滑移率

式中：v为各轮纵向轮心速度；ω为车轮转速。

2 月壤参数估计器

不同月壤参数的变化对载人月球车牵引力、驱动力矩和垂向载荷的影响不尽相同，要确定需要识别参数。描述月壤力学特性的参数包括月壤内聚力c、内摩擦角φ、内聚力变形模量kc、摩擦变形模量kφ以及切变模量j0。其中，内聚力c对于月球车牵引和力矩的影响很小，而内聚力c对牵引力和力矩的取值很敏感，本文不考虑对内聚力c的识别，在参数识别过程中给定一个合理值。其他月壤力学参数内摩擦角φ、内聚力变形模量kc、摩擦变形模量kφ以及切变模量j0，取值变化对于车轮牵引力和力矩的影响比较明显，对内聚力变形模量kc和摩擦变形模量kφ统一考虑，令kp＝kc／b+kφ。选择内摩擦角φ、系数kp以及切变模量j0作为待识别参数［6］。

无迹卡尔曼滤波算法（Unscented Kalman Filter，UKF）是由无迹变换（Unscented transform，UT）和线性卡尔曼滤波算法共同构成的。无迹变换应用了高斯分布原理，其本质是：在原始的状态量数据中根据特定的标准来获取部分采样点，采样点的均值、协方差矩阵和原始状态数据保持一致；将其代入非线性状态空间，可获得映射的非线性状态空间点集，根据原始点的选取规则，获得UT 后的均值与协方差矩阵。根据高斯分布的原理，可获得非线性系统精确到三阶的UT 后的后验均值及协方差矩阵［13］。

UKF算法步骤：

步骤1滤波初始化

式中：¯x0为初始状态；P0为初始协方差矩阵；E为求均值。

步骤2UT。UT 是在原始自变量数据附近按特定规则选取sigma点，使得sigma点的数据均值和协方差矩阵与原始自变量一致，即通过选取的sigma 点近似原始自变量；将采集到的sigma 采样点数据代入非线性函数，得到因变量的均值和协方差矩阵。对于非线性变换y＝f（x），状态量为n维，已知其均值¯x 和协方差矩阵P，可采用UT变换来得到2n+1 个sigma点和对应的权值计算因变量的统计特征。

2n+1 个sigma采样点

采样点相应的权值

式中：n为状态量维数；λ为缩放比例因子；α为较小正值，其决定了Sigma 点的分布状态；β 为非负的权系数，可合并方程中高阶项的动态误差。

步骤3 根据k时刻2n+1 个sigma 采样点计算k+1 时刻均值和协方差矩阵

式中：f为系统过程方程；qk为过程噪声；Qk为过程噪声协方差。

步骤4 将sigma 采样点代入测量方程h得到预测观测值

步骤5 根据预测观测值加权求和，得到系统预测均值、因变量协方差以及自变量与因变量的协方差：

式中：rk为测量噪声；Rk为测量噪声协方差。步骤6 更新卡尔曼滤波增益

步骤7 更新系统状态和协方差

尽管UKF对非线性系统有较高的估计精度，但存在一个问题，就是需要提前知晓系统噪声统计特性。如果系统噪声或者噪声统计特性存在偏差，则可能导致系统估计方差偏大，使得滤波发散。

Sage-Husa 自适应无迹滤波算法（Adaptive Unscented Kalman Filter，AUKF）是在UKF 的基础上，在递推滤波过程中，利用采集到的信息，在时变噪声估值器作用下，实时估计和更新非线性系统的过程噪声与测量噪声的均值和协方差，以达到减小系统估计误差、增加滤波准确度和减少滤波发散［14］。使用AUKF对月球车行驶过程中系统过程噪声和测量噪声的估算步骤：

步骤1计算系统过程噪声均值估计值

步骤2计算系统过程噪声协方差估计值

式中，ek＝yk-为残差。

步骤3计算系统测量噪声均值估计值

步骤4计算系统测量噪声协方差估计值

基于AUKF 对月壤参数进行参数识别，需搭建月壤参数识别系统的过程和测量方程。

载人月球车在月面实际行进途中，由于设定的2个估计时刻之间的间隔很短，可认为2 个估计时刻之间月壤参数维持同一个值不变，故系统过程方程

车轮垂向力、牵引力和力矩作为测量过程求解月壤参数，3 种力可由月球车配置的力／力矩传感器获得，测量方程：

3 Adams／Simulink仿真

Adams是一款系统动力学仿真软件，广泛应用在各大汽车厂商和研究院所，其仿真分析功能十分强大，涵盖范围广，能满足用户建模的不同需求，其中Car模块包含了一系列的车辆仿真专用模块，可用来快速建立样车模型，并对其各种功能指标进行评价。在Adams 建立的模型还可与其他软件如Matlab、Solidworks、Pro／E 等进行交互，实现联合仿真。在Adams建立的月球车模型如图2 所示。

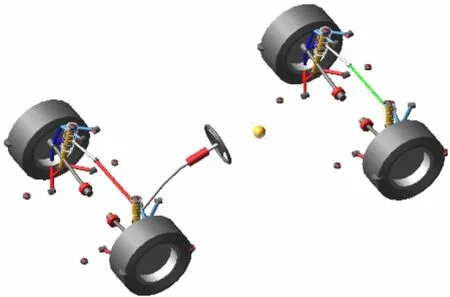
图2 月球车Adams模型

为验证基于AUKF月壤参数估计算法的准确性，建立Adams／Simulink联合仿真模型，本节选择月球车以18 km／h的恒定纵向车速分别在月壤1 和月壤2 行驶，其中估计器的3 个目标参数发生变化，其余参数不变（见表1），通过设计的AUKF 估计器可得到月壤的参数估计值，以左前轮为例，月壤参数估计器和实际值仿真结果对比如图3 所示。

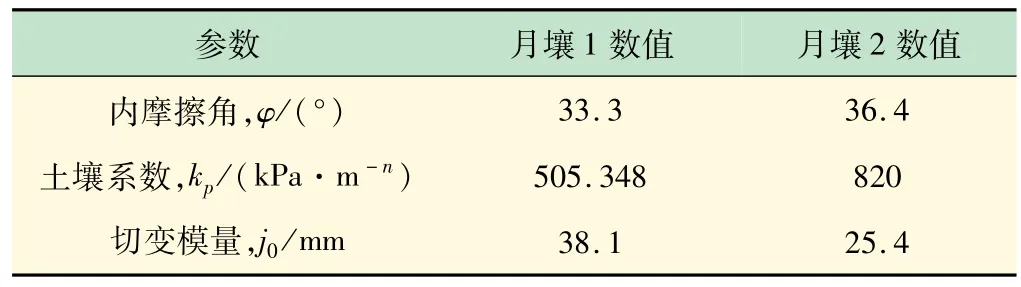
表1 两种类型月壤参数［15］

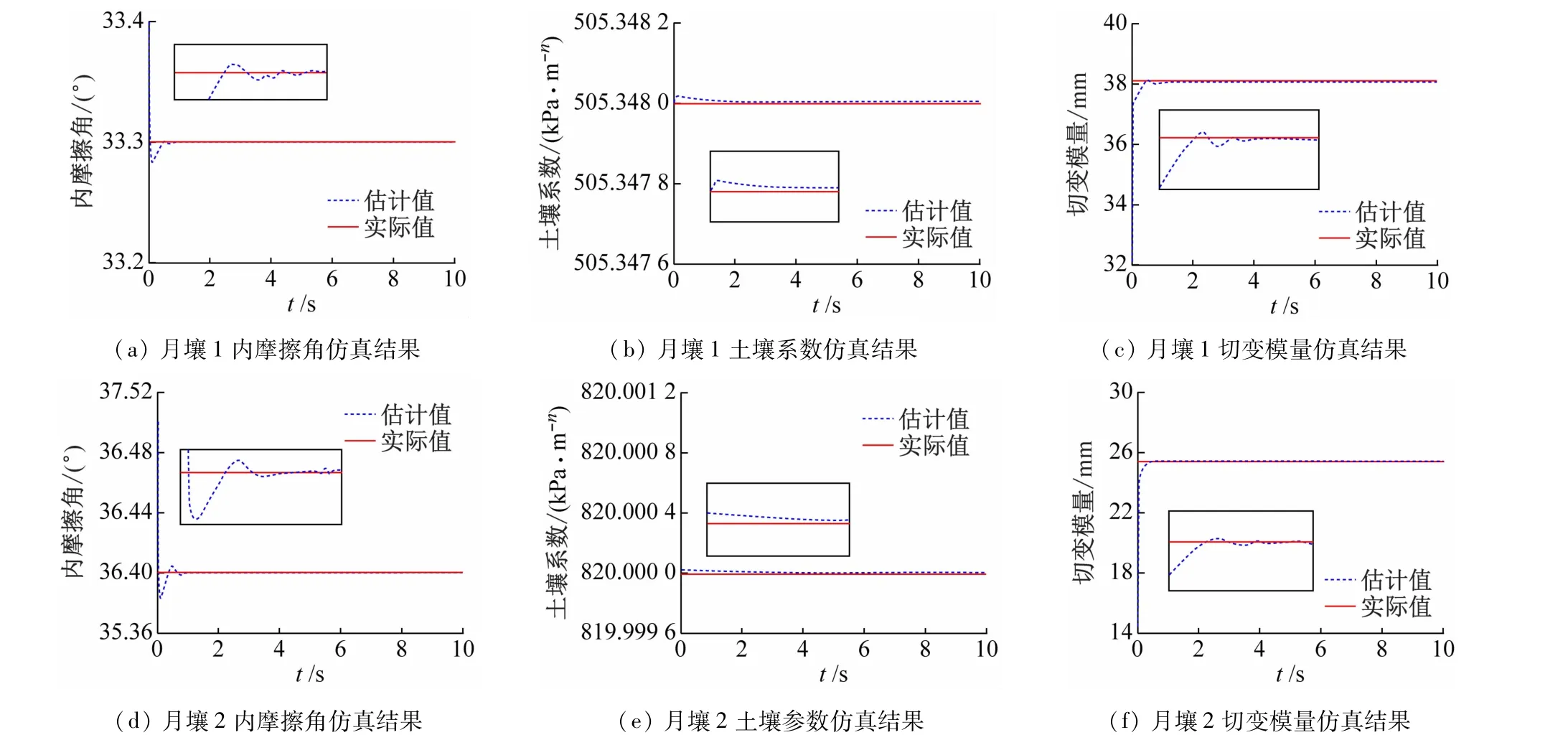
图3 月壤参数估计结果

由仿真结果可见，估计器设置的初值和月壤实际参数有所不同，无论是月壤1 还是月壤2，基于AUKF的月壤参数估计算法都可在0.5 s左右波动后收敛到真实值附近，且随后一直保持稳定。因为月壤参数估计器采用的轮壤模型对实际模型有所简化和月球车仿真中轮壤作用关系存在一定差值，因此月壤参数估计器的估计结果和实际月壤参数之间会有一定误差，结果收敛后的差值很小，误差在2%以内。

4 结语

（1）本文提出基于AUKF 的月壤参数估计方法，并进行了联合仿真。

（2）建立月球车行驶过程中轮壤模型并进行简化，设计AUKF 估计器，通过车轮力／力矩对月壤力学参数内摩擦角φ、系数kp以及切变模量j0进行估计。

（3）ADAMS／Simulink 联合仿真结果表明所设计的估计算法能够有效识别月壤参数。