磁致旋光效应测量透明液体浓度的装置设计

胡宇阳， 郑大怀， 宋柏君， 魏鸿儒， 步献东， 王晓杰，b

（南开大学a.物理科学学院；b.基础物理国家级实验教学示范中心，天津 300071）

0 引言

透明液体浓度测量在化工、制药等领域应用广泛。大学物理实验教学中，测量液体浓度的常见方法有折射率法［1-2］、干涉法［3-4］、光栅法［5-6］、荧光光谱法［7］、介电常数法［8］、光谱法［9-10］、声速法［11］、旋光法［12-13］等。其中，应用较广的阿贝折射法只能测量折射率比玻璃低（测量范围：1.3 ～1.7）的溶液。荧光光谱法利用不同浓度溶液的特征峰强度不同，具有较高的分辨率。

本文设计了一种测量分辨率高、应用范围广的透明液体浓度测量装置。引入可调节偏振片以解决简单正交偏振场标定时旋光角测量误差较大的问题；并通过消光法减小偏振片确定正交位置时所产生的误差，提高测量分辨率。同时，利用磁致旋光效应的非互易性，实验验证引入反射腔可实现在低磁场强度下精确测定液体浓度。

1 实验原理

1.1 磁致旋光效应

自然状态下，许多材料都具有旋光性，比如，石英、蔗糖溶液等。对于不具有旋光性的物质，可通过人工方法（应力、电场、磁场等）使其产生旋光效应。在磁致旋光效应中，当平面偏振光穿过置于磁场中的介质时，振动面的转角满足［14-15］：

式中：α为旋光角；V为介质的Verdet 常数，与介质属性（如浓度）和入射光波长等相关；B为磁场强度；l为线偏光在介质中走过的路程。

利用Malus定律测量线偏光经过透明液体产生的旋光角，一般将检偏器和起偏器调至正交，可得到光线偏振面旋转α，并计算出射光强

式中，Iin则为入射光强。

由式（2）可知，通过测量检偏器前后光强，可计算出旋光角。确定旋光角后，就可得到材料的Verdet 常数。此外，也可以将检偏器换成带有螺旋测微手轮转动的检偏器，在施加磁场前后，通过旋转检偏器手轮找到消光位置，通过计算2 次位置之差Δx即可得到α。对检偏器手轮位置x和检偏器角度η进行定标，可得：

式中，b为未知量，可以通过数据拟合得到。η ＝π／2时对应的手轮位置为消光位置。

利用MaLus定律可得：

将溶放置在磁场中间，实验过程中分别测量有无磁场时手轮处于不同位置的检偏器后透射光光强。利用式（4），在无磁场时，α ＝0，可得到b；有磁场时，可得到α，进而求得Verdet常数。

1.2 反射腔对磁光效应的增强

由于材料的Verdet常数大多较小，简单的通过测量旋光角的方法很难精确测量。研究表明，光的传播方向反转时，法拉第旋转的左右方向互换。因此，反射镜将经过样品的线偏光反射，再次经过样品后，旋光角将变成原来的2 倍，即磁致旋光效应具有非互易性［12-13］，如图1 所示。据此，为了增大旋光角，通过引入反射腔让光在腔内多次反射。

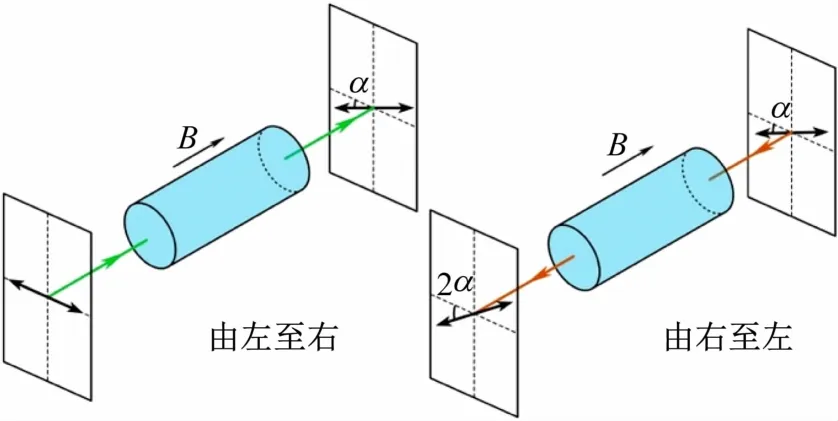
图1 磁致旋光效应的非互易性原理

（1）DPR 型反射腔。双部分反射镜（Double Partial Reflector，DPR）型反射腔两侧为部分反射镜，其结构如图2 所示。为清楚表示光线传播轨迹，光线按一定角度倾斜入射。

图2 DPR型反射腔结构

光束在由2 片部分反射镜构成的腔内多次反射，并从右侧输出。入射光强为I0，通过检偏器后可得：

式中：RP1和TP1，RP2和TP2分别为部分反射镜1、2 对应的光强反射率和透过率；β 为光线通过介质1 次时的光强透过率。在反复经过n次反射腔后，DPR型反射腔的出射总光强

（2）PTR 型反射腔。梁忠诚等［16］提出了一种部分反射镜-全反射镜（Partial Reflector-Total Reflector，PTR）型反射腔，其结构如图3 所示。反射腔由一部分反射镜和全反射镜组成，光线经分束镜后进入被部分反射镜分成2 束。第1 束光经分束器直接进入检偏器，第2 束光继续在腔内反射。

图3 PTR型反射腔结构（忽略了返回入射光方向的光线）

通过检偏器后的各级出射光强分别为：

式中：RB、TB分别为分束镜的反射率和透射率；RP，TP分别为部分反射镜的反射率和透射率。在反复经过反射腔后，PTR型反射腔的出射总光强

（3）DTR 型反射腔。本文提出的双全反射镜（Double Total Reflector，DTR）型反射腔，利用2 个反射镜和1 个分束镜设计了一种反射腔结构，结构如图4所示。入射光经过分束镜后分为2 束光，第1 束光直接射入检偏器（图中未画出），第2 束光继续在腔内反射。第1 次反射出射激光（黑色实线）光强为I1，第2次反射出射激光（橙色实线）光强为I2，以此类推。

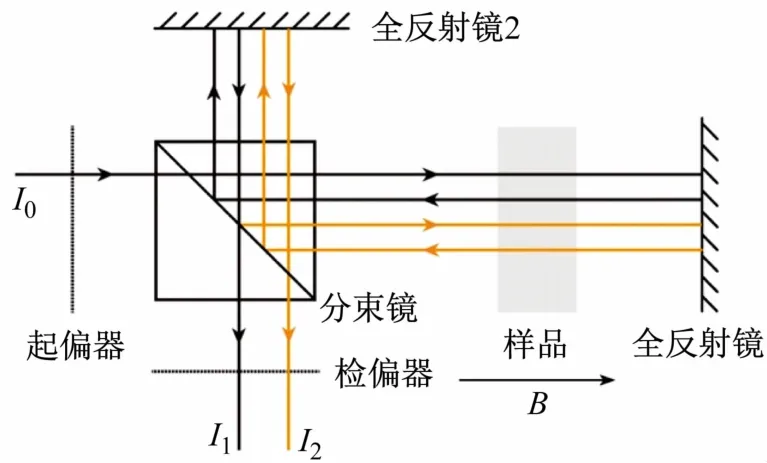
图4 DTR型反射腔结构（忽略返回入射光方向的光线）

通过检偏器后的各级出射光强分别为：

式中，RB、TB分别为分束镜的反射率和透射率。

在反复经过反射腔后，DTR 型反射腔的出射总光强：

为对比不同反射腔在本实验中的增强效果，在相同入射光强（P＝20.00 mW）条件下，计算了上述3 类反射腔出射光强与NaCl溶液质量分数c的变化关系，结果如图5 所示。其中，分束镜和部分反射镜的透过率和反射率均为0.50，β ＝0.90，IM为不加反射腔的出射光强。

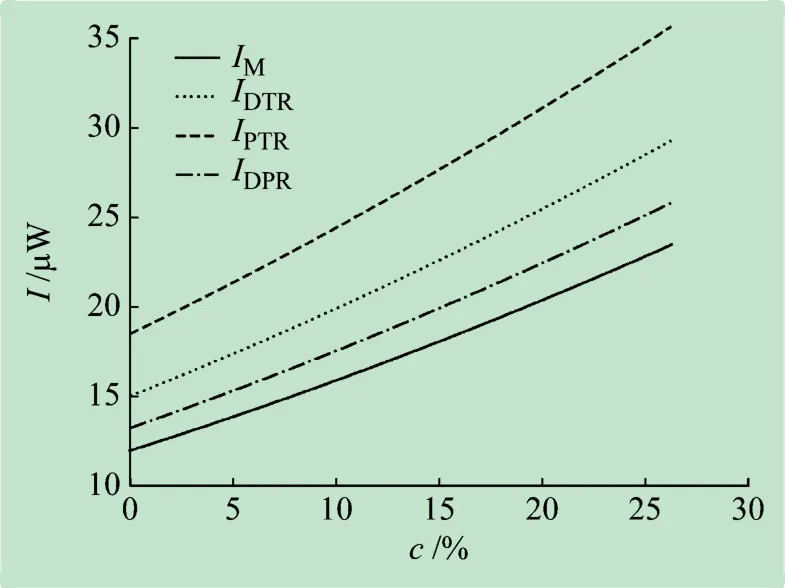
图5 不同反射腔出射光强随c变化关系

由图4 中可知，3 类反射腔出射光强关系为：IPTR＞IDTR＞IDPR＞IM。PTR 型反射腔相较于其他两类腔和不引入反射腔，其出射光强变化最大。相较于不加反射腔，PTR型反射腔出射光强增大约1.5 倍。因此，在后续通过引入反射腔增大旋光角的实验中选用PTR型反射腔。

2 实验部分

2.1 实验装置

本实验使用的主要仪器：MGL-III-532 半导体激光器，λ ＝532 nm，输出功率为20.00 mW；WDS-50 电磁铁；CH-1500 特斯拉计，分辨率为10 μT；PM100D光功率计，分辨率为0.01 μW；千分尺型偏振片，手轮分辨率为0.033°；分光棱镜，分光比1∶1；半透半反镜，反射率为0. 500，透射率为0. 500；全反射镜，反射率为0.996；石英比色皿，内径为10. 00 mm，壁厚为1. 00 mm；游标卡尺，分辨率为0.02 mm。本文以NaCl溶液为例开展实验研究，配置c（NaCl）的范围为0% ～20%。

2.2 标定NaCl溶液c与其Verdet常数关系

图6 所示为基于磁致旋光效应测量液体浓度测量装置示意图。激光经过起偏器后透射过样品并经过检偏器输出，起偏器起偏方向和检偏器的透振方向至正交，样品置于恒定磁场中。

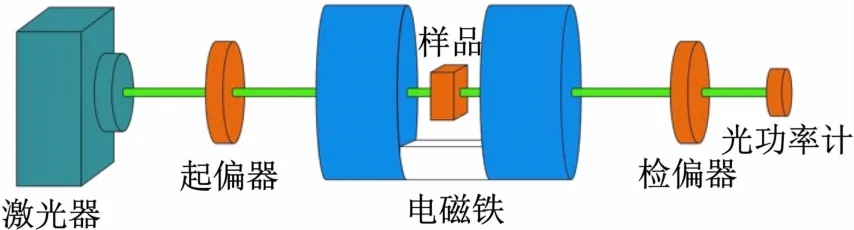
图6 基于磁致旋光效应测量液体浓度测量装置示意图

2.2.1 MaLus定律法

在开启磁场条件下，分别测量检偏器前后光强Iin和Iout，由式（2）可得到某c下的Verdet常数；再改变c重复上述操作，获得其Verdet常数。

2.2.2 消光法

将图6 检偏器换成带有螺旋测微手轮转动的检偏器。将某一c的NaCl溶液放置在磁场中间，实验过程中分别测量有无磁场时手轮处于不同位置的检偏器后透射光光强。利用式（4），分别对在有无磁场时的实验结果进行拟合，可以得到旋光角α，进而得到Verdet常数。

改变c重复上述实验可以得到不同c（NaCl）的Verdet常数。利用线性拟合得到Verdet常数与其c的关系。

2.3 反射腔实现磁致旋光增强效应

图7 所示为PTR 型反射腔的实验装置。样品置于恒定磁场中，检偏器和起偏器已调至正交，光学腔由部分反射镜和全反射镜构成。激光经过起偏器、分束镜、部分反射镜后透射过样品，被全反射镜反射后再次透射过样品。这束激光被部分反射镜分成2 束，第1束输出到探测器上，第2 束在腔内继续反射。将c（NaCl）＝5%的溶液置于磁场中间，测量旋光角α，进而得到Verdet 常数。换用不同磁场强度重复上述实验可以得到不同磁场强度下NaCl溶液的Verdet常数。

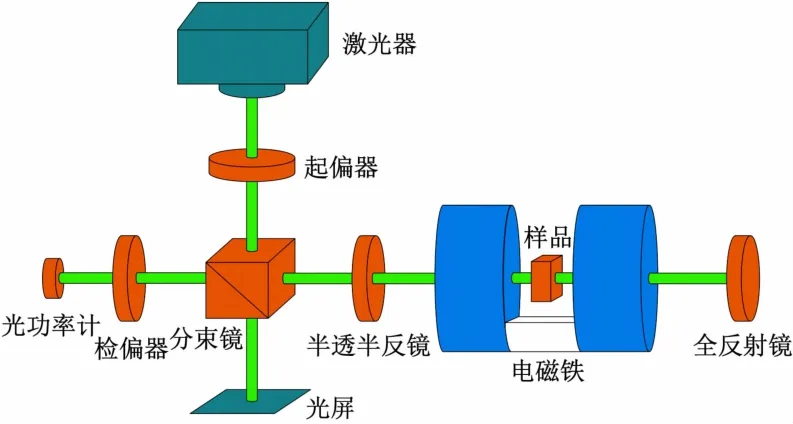
图7 反射腔下磁致旋光增项效应的实验装置示意图

3 实验结果与分析

3.1 标定NaCl溶液c与其Verdet常数关系

3.1.1 MaLus定律法

图8 所示为532 nm 波长激光下，NaCl 溶液的Verdet常数随c的变化关系。用线性拟合得到Verdet常数与c的关系。

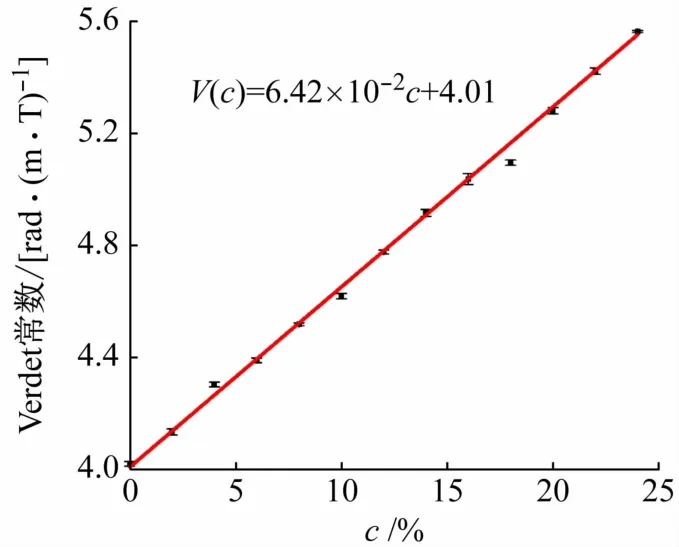
图8 在波长激光532 nm下标定NaCl溶液Verdet常数与c关系

3.1.2 消光法

将c（NaCl）＝4.50%的溶液置于磁场中间，实验过程中分别测量有无磁场时手轮处于不同位置的检偏器后透射光光强，得到实验结果，如图9 所示。利用式（4），在无磁场时，α ＝0，可以得到未知量b＝19.73；有磁场时，可得到旋光角α ＝0.043 rad，进而得到Verdet常数为5.58 rad／（m·T）。

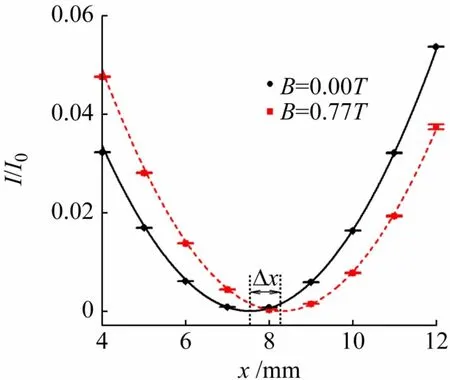
图9 有无磁场时，光强-手轮位置曲线

换用不同c（NaCl）溶液重复上述实验可以得到不同c对应的Verdet常数，结果如图10 所示。利用线性拟合得到Verdet常数与c的关系。

图10 消光法下标定NaCl溶液Verdet常数与c关系

3.2 NaCl溶液c的测量

为了验证实验装置的可行性及准确性，本实验中配置了4 种c（NaCl）＝4%、7%、14%和18%溶液，作为待验证液体（分别记为液体1、液体2、液体3、液体4）。使用消光法测量待验证液体的Verdet 常数，并结合图中标定成性拟合关系式得到待测液体的c0，结果如表1 所示。由表可知，对于NaCl 溶液，利用消光法得到的误差较小，均在6.0%以内。

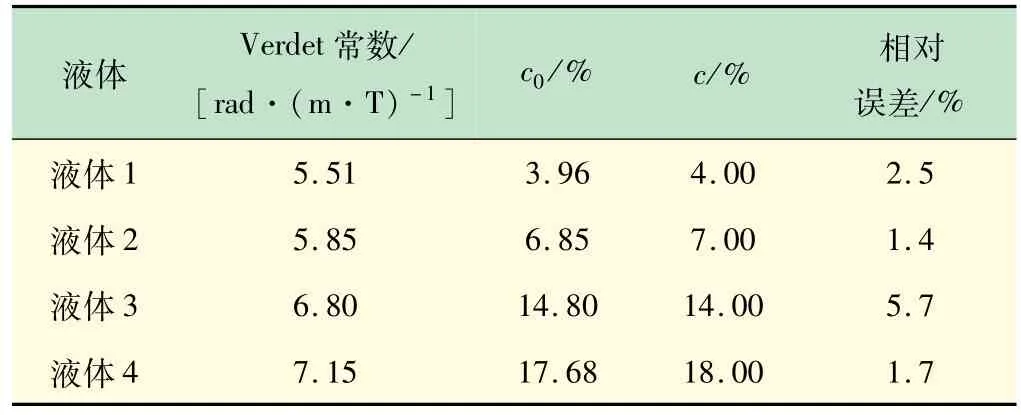
表1 不同待测液体的c与c0 对比

3.3 反射腔实现磁致旋光增强效应

利用该装置测量c（NaCl）＝5%溶液在不同磁场强度下Verdet 常数，在同一磁场强度下测量了6 次，并利用误差棒表示测量值与均值的偏差，结果如图11所示。结果表明：在不同磁场强度下反射腔实验测得指定c（NaCl）溶液的Verdet 常数相近；在低磁场强度（0. 30 ～0. 50 T）下测量准确度与较高磁场强度（0.70 ～0.80 T）时相当；当磁场强度小于0.20 T 时，即使引入反射腔，由于旋光效应较弱仍不能准确获得旋光角。

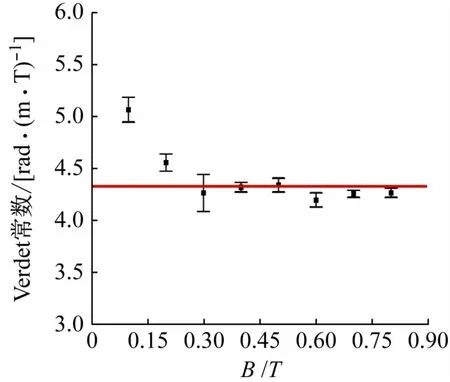
图11 当c（NaCl）＝5%时不同磁场强度下Verdet常数测量偏差

通过调研发现，磁场强度到达0.20 T以上相对容易实现，运用反射腔增强磁致旋光效应后，运用磁致旋光效应测量透明液体浓度的装置更容易推广、成本更低、测量分辨率更高。

3.4 仪器分辨率分析

利用Malus定律测量透明液体浓度，由式（2）可得Verdet常数的分辨率为0.18 rad／（m·T），由线性拟合关系，可以计算出c的测量分辨率为2.80%。

通过消光法测量透明液体浓度，由式（4）可得Verdet常数的分辨率为0.13 rad／（m·T），由Verdet常数与c的关系，可计算出c的最高测量分辨率为1.08%。结果表明：使用检偏器螺旋测微手轮转动检偏器，在检偏器消光位置附近取多点测量出射光强，并通过数据拟合得到消光角，可显著提高旋光角的测量分辨率。

引入反射腔后，利用消光法测量旋光角时，式（7）修正为

式中，δ为旋转偏振片引起的附加角度。化简可得：

式（13）左右两边同时对α求导可得：

为计算最高测量分辨率，令δ ＝0。对于纯水，旋光角最小，其实验测量值α≈0. 030 rad。代入参数RB＝0.436，TB＝0.509，TP＝RP＝0.500，得c的测量分辨率最高为0.28%。

从上述分析中可知，实际测量分辨率与最高分辨率存在一定差异，这主要是在本文实验过程中存在一定的干扰因素。例如由于电磁铁发热可能会导致磁场强度不稳定，所用光学元件存在一定的吸收和反射，c较高时NaCl溶液分布不均匀等。

4 结语

本文运用磁致旋光效应设计了测量透明液体浓度的装置。通过标定透明液体浓度与其Verdet 常数的关系，并实验测量透明液体浓度。结果表明：①使用带有螺旋测微手轮转动的检偏器，在检偏器消光位置附近取多点测量出射光强，并通过数据拟合得到消光角，可以显著提高旋光角的测量分辨率；②对于NaCl 溶液，c的测量分辨率为1.08%，不确定度为0.40%，测量范围为0% ～20%；③PTR 型反射腔能实现磁致旋光效应增强，在（0. 30 ～0. 50 T）低磁场强度与（0.70 ～0.80 T）高磁场强度有相当的测量准确度，并且在高磁场强度下c的最高测量分辨率可达0.28%。

未来实验中将考虑措施进一步优化仪器分辨率：①采取温控措施对电磁铁进行温度控制；②考虑光学元件的吸收率和反射率对测量结果的影响；③对于高c的NaCl 溶液在实际测量前进行了充分搅拌混合均匀。

本文综合运用光学、电磁学等知识研究了基于磁致旋光效应测量透明液体浓度的问题，既能够加深学生对相关理论知识的理解和应用，该装置可用于大学物理实验教学中。