切坡角度及含水率对江西上饶黏土质边坡稳定性影响的有限元模拟

陈振平， 毕晨洁， 吴珍云， 石祖峰， 李希星， 欧阳海金

（1.东华理工大学a.水资源与环境工程学院；b.地球科学学院；c.江西省防震减灾与工程地质灾害探测工程研究中心，南昌 330013；2.江西省地质局第八地质大队，江西 上饶 334000；3.江西省地质局物化探大队，南昌 330025）

0 引言

在南方丘陵区工程建设中，临近山体修路或切坡建房易形成较大边坡或者高陡切坡［1-2］。这类边坡坡高多集中在200 m内，坡度以20° ～50°为主，坡体稳定性差，在内外地质应力作用下极易产生失稳形成不同程度的地质灾害，对居民生活及交通干线等带来威胁［3-4］。针对上饶地区地质灾害类型，已有研究人员做过大量现场调查工作，统计结果表明区内地质灾害类型主要为土质滑坡，约占灾害总数的60%，且每年的3 ～7月份（汛期）为灾害多发期［1-3］。该类土质滑坡多为第四系残坡积及崩坡积物，岩性主要为粉质黏土［3］，土体结构松散，通常具有压缩性高、强度差、裂隙发达等特性［5-7］。调查结果可知地质灾害发育除了边坡本身黏土质特征之外，降雨及频繁人类工程活动（如切坡）也是重要的影响因素。但对于降雨和切坡工程如何影响上饶丘陵地区黏土质边坡失稳，目前仍没有开展相应的实验研究，尤其是从实验模拟的角度进行影响因素分析。

近年来，随着计算机模拟研究的不断深入，结合研究区实际工程地质特征，利用有效的模拟手段，基于定量分析方法对边坡稳定性影响因素进行不同角度的机理性分析，是当下研究边坡稳定性及其影响因素的有效方法之一［8-9］，如吴江鹏等［10］基于人工开挖以及降雨条件的影响，分析边坡在不同开挖时步和不同工况下的稳定性及变形破坏机理，李效萌等［11］针对赣东地区牵引式残坡积土质滑坡，利用反演分析和折线滑动法，探讨了滑坡在自重、暴雨加自重的两种不同工况下的稳定性，并分析其成因和失稳破坏模式。鉴于此，针对上饶丘陵地区开展黏土质边坡稳定性研究，有利于加深对江西境内地质灾害孕灾地质条件、成灾模式、易发性和危险性的认识，是完善境内地质灾害风险评估的重要内容之一。

本文以江西省上饶丘陵地区典型粉质黏土边坡为研究对象，以边坡坡度和含水率为控制变量，设计边坡失稳有限元模拟实验，拟分析在不同切坡角度和不同含水率下的边坡稳定性特征，以期对上饶地区边坡工程防护提供理论指导。

1 数值模拟

1.1 基本原理

ANSYS 作为一种大型的通用有限元数值模拟软件，广泛运用于各个领域［12］，在边坡工程分析中也得到了广泛应用，其中边坡稳定性分析中常见的方法为强度折减法。强度折减法是极限平衡法思想下一种新的求解边坡稳定安全系数的分析方法［13-14］，是从边坡内因进行分析，主要通过不断增加强度折减系数F，从而降低边坡的抗剪强度参数，直至边坡达到临界平衡状态。临界平衡状态下对应的F即为边坡整体处于稳定的安全系数ns，在折减过程当中，抗剪强度参数需要满足下列关系式：

式中：C、φ分别为折减前岩土体的黏聚力、内摩擦角；i为折减次数；Ci、φi分别为折减后岩土体的黏聚力、内摩擦角；Fi为强度折减系数。

在有限元分析应用中，滑动土体无限移动，以特定监测点的应变和位移突变且无限发展作为边坡失稳破坏的依据［14］。本文中使用该方法作为数值模拟过程中边坡失稳破坏的依据。在边坡稳定性分析当中，一般认为边坡的ns＞1.0 时，边坡是稳定的；ns＜1.0 时，边坡发生失稳破坏；ns＝1.0 时，边坡处于极限平衡状态。

1.2 模型建立与参数设置

上饶地区土质滑坡组成以碎石土、粉质黏土及含碎石粉质黏土为主，结构松散，其厚度一般为0.3 ～15 m之间，属浅层滑坡，受外界因素的影响，极易以牵引式运动形式发生滑脱，多具上小下大的格局，横向张性裂隙发育，表面多见阶梯状或陡坎，如图1 所示。针对研究区土质边坡的几何特征，结合上饶地区野外边坡调查结果，本文建立了如图2 所示的模型。简化后的初始模型条件为底高40 m，宽115.15 m，坡高为20 m，并用3 个算例条件进行分析，算例的条件如下：

图1 上饶地区典型黏土质边坡（滑坡）

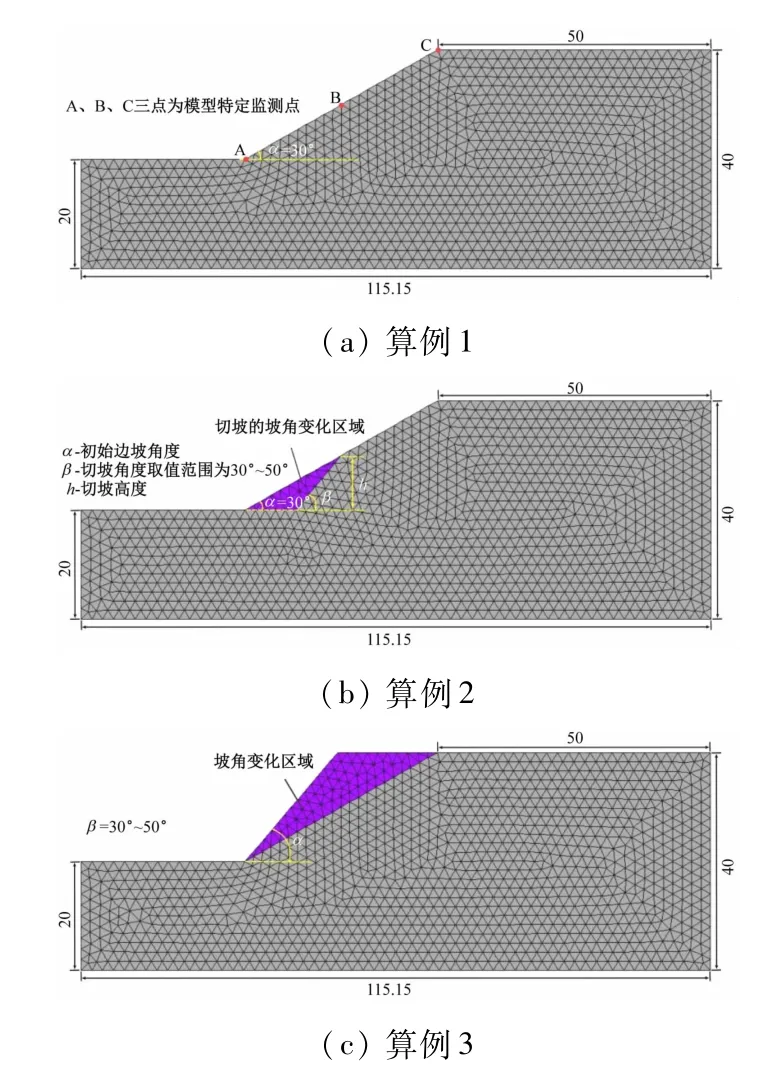
图2 建立的模型条件（m）

算例1为对比模型，设定初始边坡角度α ＝30°［见图2（a）］。

算例2基于算例1 中边坡的参数和几何形态，固定切坡高度为10 m，以切坡角度β ＝30° ～50°（初始角度为30°）为变量计算了不同切坡角度下边坡稳定性实验［见图2（b）］。

算例3在算例1 模型基础上，以特定坡角下不同含水率w为变量，模拟分析了边坡的稳定性［见图2（c）］。实验设计中根据统计的研究区岩土工程勘察所提供不同含水率下土体的抗剪强度参数，确定算例3 模型的力学参数，进而将降雨量对边坡稳定性影响转化为土层含水率变化导致土体抗剪强度参数变化对边坡稳定性的影响。

模拟实验基于ANSYS 软件［12］，采用Drucker-Prager模型［15］，屈服准则选择M-C 准则［16］，基本参数采用粉质黏土的力学参数（如密度ρ、弹性模量E和泊松比ν），3 个算例模型具体参数见表1 所示。模型采用二维平面单位中的plane82，网格划分采用三角形或四边形网格单位，在坡趾、坡中、坡顶分别设置A、B、C 3 个监测点，边坡简化模型与监测点位置如图2（a）所示。边界约束条件的设置是否正确与模拟能否计算成功有很大关联，模型的左右边界只有水平方向约束，底部边界设置为所有方向约束，顶部边界不进行约束，且外部荷载只有重力荷载。

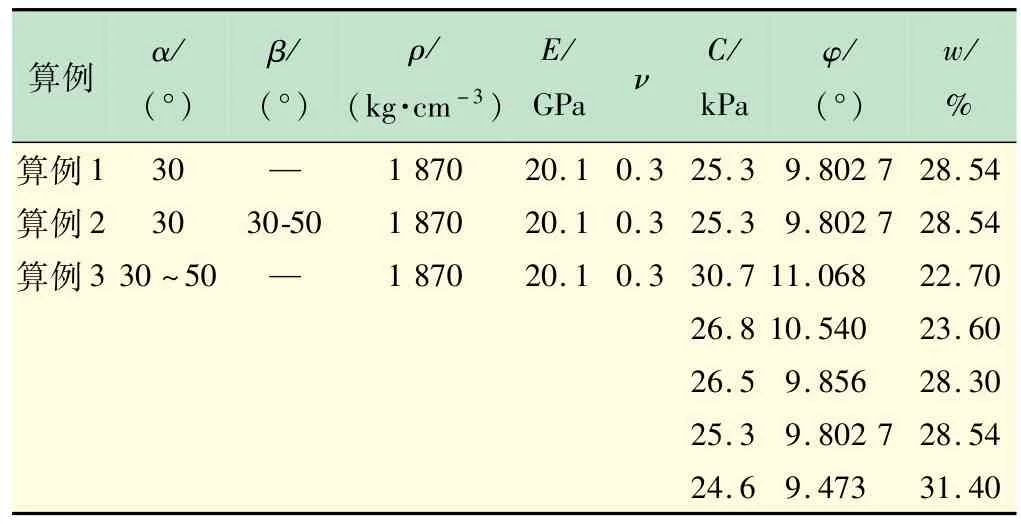
表1 不同算例土体的物理力学参数

2 有限元计算结果与分析

2.1 有限元计算结果

2.1.1 算例1

算例1 模型中分别选取A、B、C 点作为位移突变的监测点，观测3 点在不同强度折减系数下位移的变化，如图3 所示。同时绘制了F与X方向位移（UX）变化关系曲线，如图4 所示。由图3、4 可知，通过对A、B、C点处边坡失稳破坏前、后的曲线进行线性拟合，发现失稳破坏前、后是呈线性相关的。于是，通过线性相关构建线性方程，可求得边坡模型的ns［9，11］。以C点处为例，获取边坡失稳破坏前、后在该点处的线性关系如下：

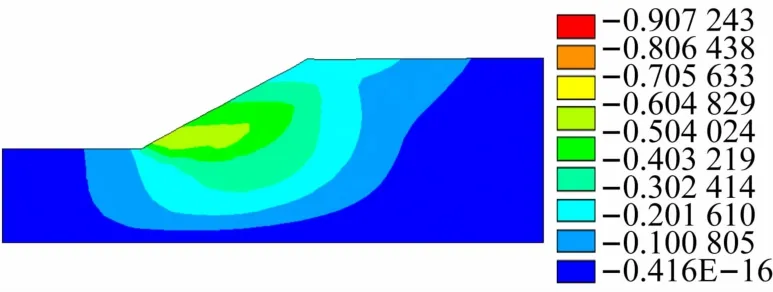
图3 算例1模型ns 状态下的X方向位移云图

图4 F与UX 关系曲线

经关联求解，解得C 点处FC＝1.187 5。同理，分别以A点、B点为位移突变监测点，计算其对应FA、FB分别为1.191 9、1.185 8。将A、B、C 点处F求取均值，即为模型整体的安全系数ng。因此，算例1 采用位移突变判据解得的ng＝1.188 4，说明此时的边坡处于稳定状态，其在自重作用下边坡不会发生失稳滑移。

2.1.2 算例2

算例2 以算例1（F＝1.188 4 时的边坡）作为切坡前的初始模型，模拟边坡在坡趾处出现切坡时的稳定性，并绘制边坡n与β关系曲线，如图5 所示。模拟结果表明，例2 模型n随β的增加总体呈现下降趋势，且临界平衡状态（即n＝1.0）时所对应的β 约为44°，这说明算例2 在β ＞44°时，其模型n＝将小于1，在自重作用下将发生边坡失稳。

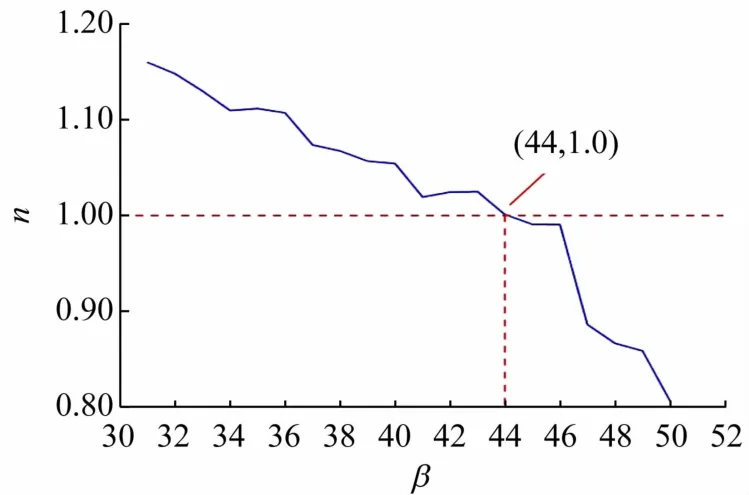
图5 β与n关系曲线

2.1.3 算例3

为了进一步分析不同坡角时黏土质边坡含水率对n的影响，本文开展了算例3 模型计算，实验模拟结果如图6 所示。由图可知，同一坡角下，n均是随着含水率的增加而降低，而在不同坡角下，边坡临界极限状态（n＝1.0 时）所对应的含水率在降低，β 越大，边坡失稳所对应的含水率越小。以处于临界极限状态的A、B、C点为例：A点（β ＝50°）失稳临界所需w＝23.3%；B点（β ＝45°）失稳临界所需w＝28.2%；C 点（β ＝40°）失稳临界则需w＞31.4%。模拟计算结果表明，受降雨影响的情况下，边坡w会发生变化，导致不同β的边坡产生不同程度的失稳。对于w＝22% ～32%的黏土质边坡，其易发生边坡失稳的β 范围在40°以上；对于β ＝45°的边坡，w＞28.2%，则边坡易失稳；β ＝50°时，w＝23.3%时，边坡便易失稳。

图6 不同β下ns 与w关系

根据研究区收集的岩土工程勘察资料，本文选取了一个常态化雨季时期（w＝28.54%）典型黏土层边坡进行了不同坡角下边坡变形模拟，如图7 所示。由计算模拟的等效塑性云图可知，当β ＝30°时，边坡未出现等效塑性区，当β ＝42°时，边坡坡趾处开始出现明显的塑性区。随着β 的增加，边坡的塑性区从坡趾处开始扩展，且边坡的临界滑动面也开始逐渐显现并存在向坡体内延伸的趋势，滑体面积也相应地逐渐增加，当β ＞44°时，边坡塑性应变值迅速增加，塑性区分布开始从坡趾向坡顶蔓延，甚至贯穿坡顶，滑动面完全形成。

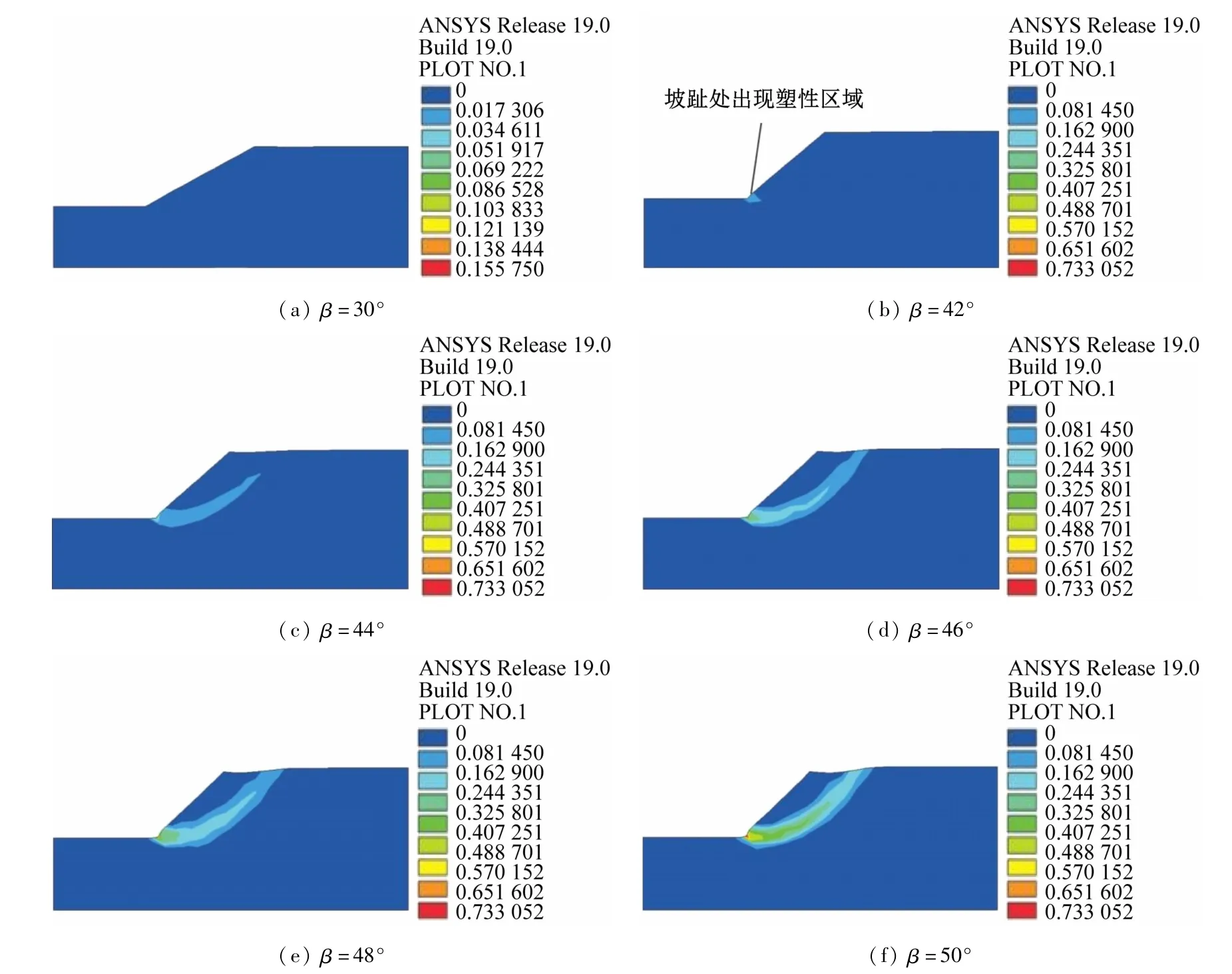
图7 w ＝28.54%下不同β的等效塑性云图

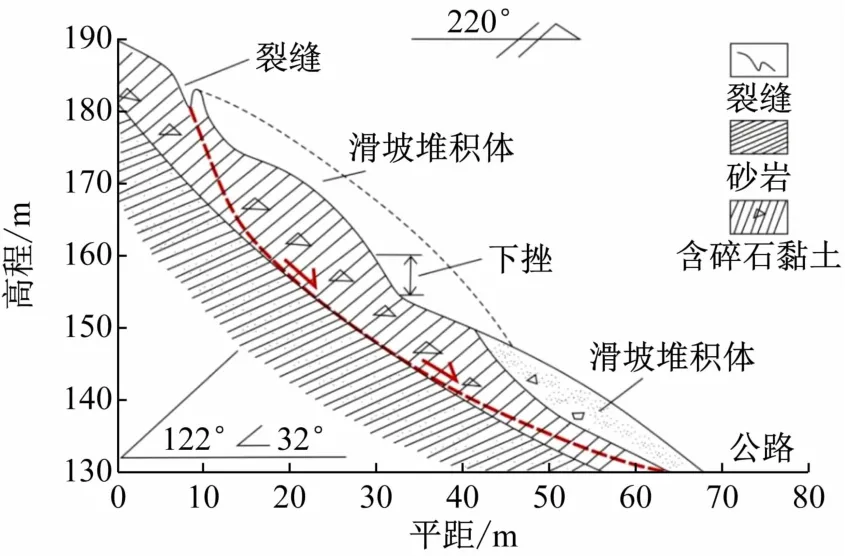
图8 上饶地区典型牵引式滑坡剖面图

2.2 结果分析

上饶地区大部分位于丘陵和低山区的居民住宅常依山而建，房屋后有不同程度的切坡现象［17］，这些切坡多为中高角度边坡，在强降雨作用下，极易使土壤含水量增加，下渗至滑面上，经渗流、冲刷等形式，地层失稳，产生蠕滑变形，发生不同程度的地质灾害［见图1和8］。算例2 和算例3 边坡模型的模拟结果很好地表现出上述情况（见图5 ～7）。算例2 中模型对坡趾处土体进行开挖，n随之降低，同时，坡趾处位移对比切坡前发生了明显的变化，β 越大，发生位移量也越大。算例3 模型中土体的抗剪强度参数（表征土层含水率）对n有很大影响，随着抗剪强度参数增加，n降低。但当β ＜40°，土质w＜31.5%时，边坡整体仍处于稳定状态。结合现阶段上饶地区土体的含水率特征，表明在受降雨影响的情况下极易发生边坡失稳的范围在β≥40°，如在β ＝45°，w＞28.54%时，边坡失稳，而β ＝50°时，w＞23.6%，边坡就失稳滑移。

结合上饶地区的工程地质环境条件、边坡特征以及本文的模拟实验，可以对区域内的土质边坡提供有针对性的防治建议：①可通过降低或平缓坡度有效改善边坡稳定性，尤其在进行边坡开挖的坡比设计时，坡比值越大，越易造成边坡滑移面的塑性区和位移值增加，造成边坡失稳破坏（Komadja 等［18］基于极限平衡法和强度折减系数的有限元方法，探讨了边坡几何形态对稳定性的影响，结果同样表明边坡整体坡角和坡高对稳定性的影响最大）；②可以增加坡面植被的覆盖率或者做好排水、防水等工程措施，防止因降雨降低土体的抗剪强度从而导致的边坡失稳破坏［19］。

3 结语

本文基于ANSYS软件，以上饶地区典型黏土质边坡为研究实例，设计了3 种条件下模型，分析了不同切坡角度和含水率条件下边坡稳定性。结果表明：

（1）在β ＝30°，w＝28.54%状态下，n＝1.188 4处于稳定状态，在自重作用下不会发生边坡失稳滑移；当坡脚处β ＝44°时，边坡处于失稳临界状态，若β 大于这个临界角度，易发生失稳滑移。

（2）当β ＜40°，土质w＜31.5%时，边坡整体处于稳定状态；在β ＝45°，w＞28.54%时，则边坡失稳；β ＝50°时，w＞23.6%，则边坡失稳。

（3）结合上饶地区边坡特征及计算模拟结果，在预防黏土质边坡发生失稳滑移上，一方面建议通过降低切坡坡度来有效改善边坡稳定性；另一方面建议增加坡面植被的覆盖率或者做好排水、防水等工程措施，防止因降雨降低土体的抗剪强度从而导致边坡失稳。