基于剪切效应的加固梁弯曲性能研究*

李政 肖珍 赵恒 刘意中

常德学院 415000

引言

在实际工程中，许多工程结构的构件由于修建年代已久远，常出现承载能力不足的情况，需要加固来维护结构的安全。为了对古代木建筑进行加固，阿斯哈等［1］研究了对木梁加固的试验；王磊［2］研究了混凝土加固梁抗弯性能；贺学军等［3］研究了自锁碳纤维间接加固混凝土框架中节点的抗震性能；陈超等［4］推导出了预应力CFRP 加固简支梁的弹性力学解析解；周朝阳等［5］分析计算了贴片加固混凝土梁界面粘结剪应力；瞿尔仁等［6］对FRP 加固混凝土梁层间应力的弹塑性进行了分析；欧阳煜等［7］研究了粘贴片加固混凝土梁的粘接剪应力。在以上关于加固梁的研究文献中，文献［1］关注对木梁加固的试验，文献［2 -7］关注对混凝土梁加固的理论研究计算，但是都未讨论剪力对均布载荷作用下加固梁弯曲变形的影响。经典材料力学理论［8，9］研究了加固梁的弯曲应力计算，但忽略了剪切对梁的影响。基于上述因素，本文讨论了剪切对均布载荷作用下加固梁弯曲变形的影响。

1 计算理论

以图1 所示均布载荷作用下加固梁为例，来讨论剪切对加固梁变形的影响。

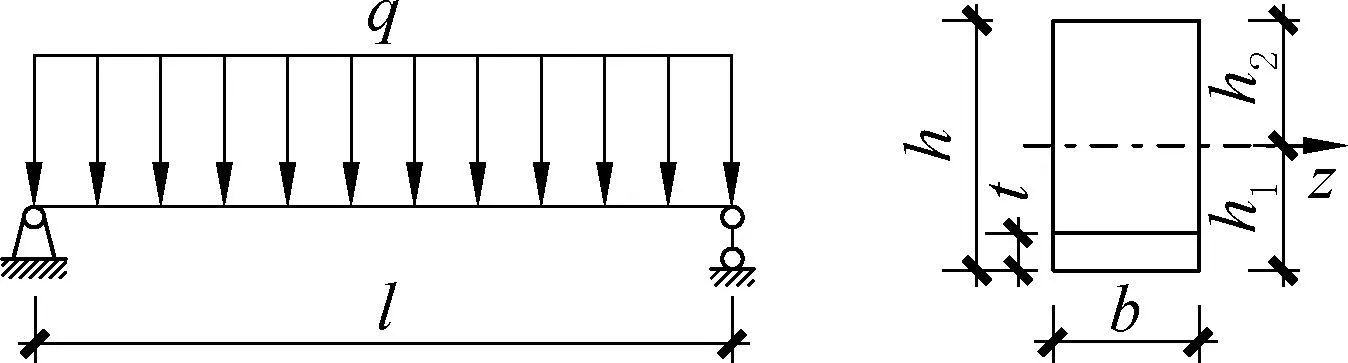
图1 加固梁Fig.1 Reinforced beam

假设加固梁在纯弯曲状态下，其跨中截面应变满足平截面假定，钢板与原梁始终保持紧密连接，未发生剥离，处于共同受力状态，且钢板与原梁均满足胡克定律。由材料力学可写出加固钢板及原梁纯弯曲的正应力为：

式中：E1、E2分别为钢梁、原梁的弹性模量；ρ为曲率半径；y为梁截面上点至中性轴的距离。由材料力学可得梁的静力方程为：

式中：b为梁截面宽度。

把式（1）代入式（2）中可得拉伸区、压缩区的高度分别为：

式中：h为原梁高度；t为钢板厚度。

利用材料力学可知梁的弯矩平衡方程为：

式中：M（x）为梁截面弯矩。

把式（1）代入式（4）中可得：

利用式（1）、式（5）可得不考虑剪切影响弯曲应力为：

假设加固钢板较薄，可认为梁截面剪力全部由原梁承担。由材料力学可知图1 所示受压区（-h2≤y≤0）的剪应力为：

式中：Q为梁截面剪力；下脚2c 代表原梁的压缩区。

为推导原梁拉伸区（0≤y≤h1）的剪应力，以图2所示加固梁微段为例，梁截面左边轴向拉力为：

图2 加固梁微段Fig.2 Micro-section of reinforced beam

同理，图2所示加固梁微段右边轴向拉力为：

由于图2 所示加固梁微段静力平衡方程为：

把式（8）、式（9）代入式（10）中可得原梁拉伸区的剪应力：

下面讨论剪切对均布载荷作用下加固梁的弯曲应力及挠度的影响。

由弹性理论可知剪应力、剪应变、横向位移、轴向位移关系为：

式中：i＝1 代表钢板，i＝2t代表原梁拉伸区，i＝2c代表原梁压缩区；G2为原梁剪切弹性模量；ui为轴向位移；w为横向位移。

把式（12）对y积一次分可得：

式中：Ci为待定常数。

加固梁的轴向位移连续条件为：

由于钢板的剪应力τ1＝0，因此把τ1＝0、式（7）、式（11）代入式（13）中且利用式（14），可得加固梁的钢板位移、原梁拉伸区位移、原梁压缩区位移为：

考虑剪切影响时，可知加固梁的弯矩平衡方程为：

把式（16）代入式（17）中，可得加固梁弯曲微分方程为：

把式（18）代入式（16）中可得考虑剪切影响时，加固梁的弯曲应力公式为：

把式（19）对x积分可得考虑剪切影响时，加固梁的挠曲线表达式为：

式中：B1、B2为待定常数。

以图1 所示简支加固梁为例，利用式（19）、式（20）可得梁中点的最大弯曲应力及中点挠度分别为：

为了检验本文方法的计算精度，令E1＝0、t＝0、E2＝E、G2＝G，且利用可把式（21）、式（22）化为：

式（23）、式（24）与文献［10］给出的结果是一样的，而文献［10］已利用弹性理论证明了式（23）、式（24）的计算精度是比较高的。

2 算例讨论

为了讨论剪切对均布载荷作用下加固梁弯曲变形的影响，下面以图1 所示加固梁为例。加固梁的计算参数为：E1＝200GPa，E2＝10GPa，G2＝0.5GPa，b＝0.15m，h＝0.2m，t＝0.012m，［σ1］＝110MPa，［σ2］＝8MPa。

把加固梁计算参数代入式（21）、式（22）中可得：

把式（25）、式（26）计算的结果列在表1、表3 中，以便讨论分析。由式（25）、式（26）可知等号右边第一项皆为材料力学解，在表1、表3括号内的数据皆为材料力学解。计算方法所得到的应力及挠度与材料力学解的误差分别列于表2、表3 中。

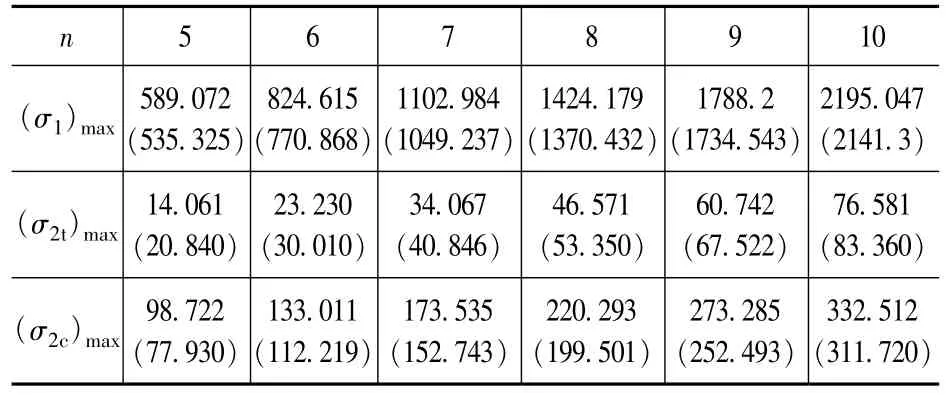
表1 梁中点应力（单位：N／m2）Tab.1 Mid-point stress of beams（unit：N／m2）

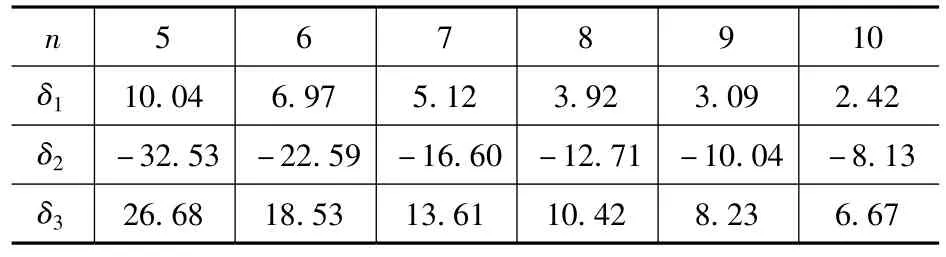
表2 梁中点应力误差（单位：%）Tab.2 Mid-point stress error of beams（unit：%）

表3 梁中点的挠度（单位：m）Tab.3 Mid-point deflection of beams（unit：m）

对表1～表3 进行分析可知：在相同均布载荷作用下，随着长高比的增大，梁中点的正应力、挠度也逐渐增大。本文方法考虑剪切影响时计算出钢板的拉应力、原梁的压应力均大于材料力学解，即使长高比n＝10 时（σ2t）max、（σ2c）max与材料力学解的误差也超过了5%；本文方法考虑剪切变形影响时计算出梁中点挠度大于材料力学解，即使长高比n＝10 时与材料力学解的误差也有40%以上。由以上分析可知，在均布载荷作用下剪切对梁挠度、正应力都有较大的影响，其中剪切对梁挠度的影响更大些。以上分析说明材料力学解存在偏于不安全的问题，还应考虑剪切的影响。

3 结论

1.相同均布载荷作用下，随着长高比的增大，梁中点的正应力、挠度也逐渐增大。本文方法考虑剪切影响时计算出钢板的拉应力、原梁的压应力均大于材料力学解。

2.在均布载荷作用下剪切对梁挠度、正应力都有较大的影响，其中剪切对梁挠度的影响更大些。以上分析说明材料力学解存在偏于不安全的问题，建议还应考虑剪切的影响。