规则接地网拓扑结构关键特征点识别与重建

吉旺威，赵宏梅，林 艺，郑服利，李国城，宋恒力，刘 欢

（1.广东电网有限责任公司广州供电局，广东广州 5 104101；2.中国地质大学（武汉）自动化学院，湖北武汉 430074；3.复杂系统先进控制与智能自动化湖北省重点实验室，湖北武汉 430074；4.地球探测智能化技术教育部工程研究中心，湖北武汉 430074）

0 引言

接地网是变电站保障电气安全的重要设备，其结构的完好是变电站维持安全运转的重要保障[1]。接地网导体材料大多数采用耐腐蚀性不高的导体，并且导体长期掩埋在复杂的土壤环境中，因此接地网导体逐渐腐蚀变细甚至断裂，接地性能下降，存在安全隐患[2-4]。如果不能及时、准确地识别接地网结构并更换导体，就可能会发生安全事故，造成损失[5]。大部分变电站年限较久，在对接地网进行故障诊断时，存在图纸丢失或者实际结构与图纸存在较大差异的情况[6-8]。通过盲目的大面积挖掘来排查断点和腐蚀区域的方法不但会造成人力和物力的浪费，而且还影响电力系统的安全稳定运行[9-10]。因此，实现在不停电、不挖掘的情况下，通过检测设备在地上对地下接地网进行检查，分析采集的磁感应数据来识别接地网拓扑结构是十分必要的。

文献[11-12]中提出了一种通过测量与接地网相连的可接地导线之间的端口电阻来诊断接地网的腐蚀状态的方法。但是这种方法不但需要图纸，而且需要详细推导所有接地导体的腐蚀状态与实际测量的端口电阻之间的数学关系。为了摆脱对图纸的依赖，学者们开始转向对接地网进行电磁场检测的方法[13-15]。电磁场检测技术的主要方法包括接触式的电场或磁场测量法和非接触式的瞬变电磁法[16]。文献[17]提出了将接地导体通入电流，探测其上方产生的磁场分量，当探测线圈平面与导体平行时，通过线圈的磁通量出现峰值，判断此处有接地导体，绘制出接地网拓扑结构。文献[18]提出了一种通过检测感应阻抗来诊断接地网腐蚀故障的方法并开发了无损检测样机。

文献[1-8]的研究为接地网拓扑结构的识别提供了有效的解决方案。但在实践中仍然存在一些困难。例如，实际测量中采集数据是非均匀的，主要原因包括2 点：人力推动仪器前进，不能保证匀速；地上变电站设备影响，导致检测仪器行进到一定位置需要停止或绕道。因此，原始磁感应检测数据通常是离散的，在进行数据处理时，需要对缺失的数据进行插值重建[19-20]。通过插值算法实现接地网磁感应数据的成像后，还需要利用相关算法针对插值后的磁感应检测数据进行接地网结构识别。目前针对接地网网格拓扑结构识别的算法有形态学滤波法、边缘检测法、感应电压微分法等，文献[21]提出通过形态学分水岭算法提取接地网拓扑结构，使用的形态学滤波算法结构元参数需要根据不同拓扑网格结构进行调整，现场施工不易操作。文献[22]针对变电站存在较大的电磁干扰这一问题，对感应磁场的磁梯度应用小波边缘检测方法提取接地网拓扑结构，该算法计算量较大且抗干扰能力差。

针对现有研究方法存在的一些不足，本文根据变电站面积大、接地网结构复杂和监测数据量大的特点[23-25]，提出了一种针对磁感应数据特点的关键特征点识别算法。采用插值算法对接地网原始磁感应数据进行处理，在得到磁感应网格化数据后，提取关键特征点，从而重建出网络结构，并通过搭建仿真模型实验以及实际测试实验对方法进行验证。

1 拓扑结构识别理论

由于磁感应数据受拓扑结构、电流强弱的影响，磁感应数据的范围不定。为了后续数据处理方便，需要对数据进行归一化处理，如式（1）所示：

式中：z为原始数据集；z′为最值归一化处理后的数据集；min（z）和max（z）为原始数据z中的最小值和最大值。

1.1 基于双三次插值的图像重建

本文参考传统插值算法在图像放缩中的应用，为解决接地网磁感应强度数据分布不均的问题，采用了双三次插值算法对原始磁感应数据进行处理。

双三次插值（BiCubic）是一种基于二维函数的插值方法，通过在小区域内进行局部插值来估计目标点的数值。一般选取目标点周围最近的16 个值进行加权平均得到目标点的插入值，各点的权重由该点到目标点的距离决定，包括横向和纵向的距离。

图1 是一个二维图像的双三次插值俯视示意图。图1 中蓝色的点为待求点，黑色的点为离待求点最近的16 个点。设待求点左上方的点坐标为（i，j），待求点距（i，j）点的横向距离为u，纵向距离为v，设待求点坐标为（i+u，j+v），已知其周围的16 个坐标点的位置及对应取值，还需要计算16 个点的权重。

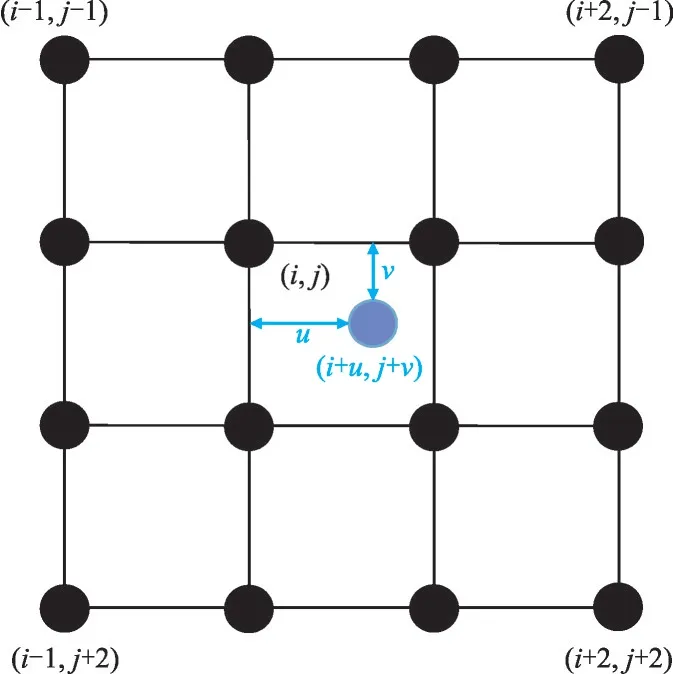
图1 双三次插值俯视示意图Fig.1 Top-view schematic illustration of bicubic interpolation

双三次插值核函数W（x）是一维分段三次多项式函数，W(x)的值即坐标点的权重值，如式（2）所示：

式中：x为已知点在X轴方向上或Y轴方向上与待求的未知点的距离；a为插值核参数。

双三次插值基函数是一维的，而像素是二维的，将像素点的行与列分开计算。例如（i-1，j-1）距离（i+u，j+v）的距离为（1+u，1+v），因此（i-1，j-1）的纵坐标权重为W（1+v），横坐标权重W（1+u），坐标（i-1，j-1）对（i+u，j+v）的贡献值为：W（1+v）×W（1+u）×（i-1，j-1）的像素值。同理可得其余15 个坐标点各自的权重。可得目标点（i+u，j+v）的值f（i+u，j+v）如式（3）所示：

式中：f（m，n）为（m，n）点像素大小；W（i+u-m）为像素点（m，n）距离（i+u，j+v）的横坐标权重；W（i+v-n）为像素点（m，n）距离（i+u，j+v）的纵坐标权重；f（i+u，j+v）为获取到的插值结果。

或者使用矩阵列式计算f（i+u，j+v），如式（4）所示：

式中：A为横向权重；B为数值矩阵；C为纵向权重。

式中：W（1+u），W（u），W（-1+u），W（-2+u）为待求点位附近16 个像素点的横坐标权重；W（1+v），W（v），W（-1+v），W（-2+v）为待求点位附近16 个像素点的纵坐标权重。

1.2 接地网拓扑结构识别算法

对整个变电站进行检测后，产生大量的接地网磁感应数据，但并不是所有数据都包含拓扑结构信息。需要根据接地网在地表上产生的磁感应数据特征，针对接地网磁感应数据选取关键特征点。

假设载流单导体磁场的分布模型如图2 所示。

图2 载流单导体磁场分布模型Fig.2 Model of magnetic field distribution in single current-carrying conductor

导体置于深度h处，土壤为磁导率μ1的均匀介质，以导体上O点为坐标原点建立XYZ直角坐标系，导体通过X轴，导体内部电流为I，P为地上的检测点，与导体的垂直距离为ρ，B为P点的磁感应信号值，Bx，By为P点水平沿X轴和Y轴上的磁感应信号值。

磁场在水平方向上的磁感应强度为：

式中：Bx，By为地表水平方向两正交方向上的磁感应信号值；μ0为真空磁导率；y为检测点P距离载流导体水平距离。

利用COMSOL Multiphysics 软件仿真图2 中的物理模型，可以得到地表水平方向上的磁场|Bx+By|分布情况如图3 所示。磁感应数据在导体正上方时，即y=0 时最大，而在远离导体的位置时磁感应数据将衰减，据此可以判断峰值点为接地导体的位置点。

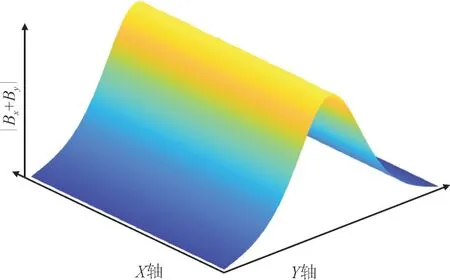
图3 单根载流导体在地表上的|Bx+By|分布情况Fig.3 |Bx+By|distribution of single current-carrying conductor on the Earth’s surface

当地下载流导体存在交叉布置时，如图4 所示。

图4 载流导体交叉布置磁场分布模型Fig.4 Model of magnetic field distribution in crossarranged current-carrying conductor

同样利用COMSOL Multiphysics 软件仿真该物理模型，可得到地表水平方向磁感应强度分布情况如图5 所示。

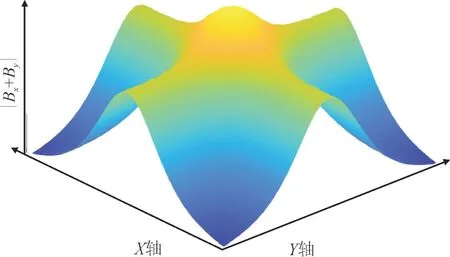
图5 2根载流导体交叉布置在地表上的|Bx+By|分布情况Fig.5 |Bx+By|distribution of two cross-arranged currentcarrying conductors on the Earth’s surface

由前面单根载流导体模型可知，水平方向上磁场强度在扁导体直上方存在峰值，因此在2根导体交叉磁场叠加后，水平方向磁感应强度会在导体交叉点的垂直正上方存在峰值。

在得到均匀分布的数据点后，为了实现对接地网拓扑结构的识别，采用将磁感应网格化数据的二维局部极大值点作为导体交叉处关键特征点，及一维局部极大值点作为地下导体位置关键特征点，融合导体交叉处关键特征点及导体位置关键特征点形成接地网拓扑结构图像，确定接地网导体位置。

根据图5 可知，在地下导体交叉处上方的磁感应数据会明显大于其附近区域，因此在得到磁感应网格化数据后，构造一定大小的二维结构元。例如在图6 中，网格内的数字代表插值处理后地表上的磁感应信号数据，其中每个网格代表地表上的一块方向区域，数值代表该区域内的磁感应信号强度，构建3×3 正方形结构元。结构元能够在网格化磁感应数据中移动，在移动得的同时判断结构元中心的数据是否大于其四周数据。若大于周围数据，则符合正交载流导体在地表上的磁场分布情况，可作为扁钢交叉处关键特征点数据进行保存。

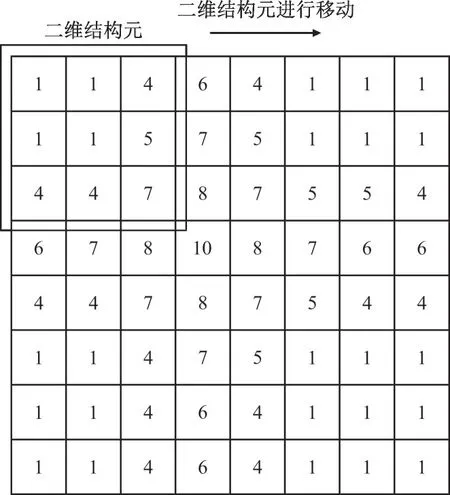
图6 结构元在磁感应网格化数据中移动并判断局部最大值Fig.6 Diagram showing structural element movement in magnetic induction grid data while determining a local maximum value

根据图3 可知，导体上方磁感应数据大于远离导体处的磁感应数据，因此在二维网格化磁感应数据中选取1 条一维数据，同样构建1 个一维的结构元。例如图7 所示，构建1 个容量为3 的结构元。

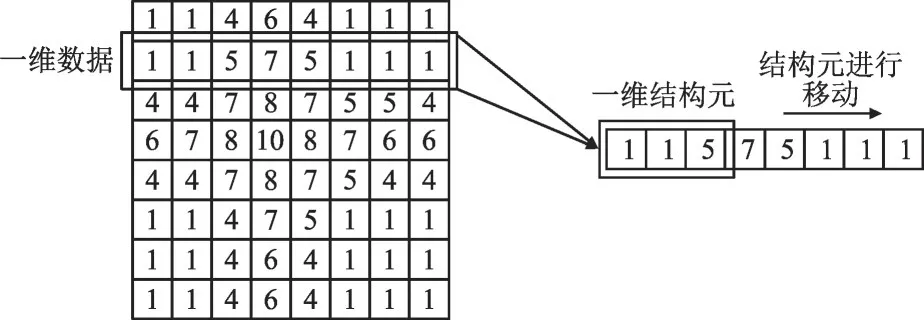
图7 一维结构元在一维磁感应网格化数据中移动同时判断局部最大值Fig.7 Diagram showing one-dimensional structural element movement in one-dimensional magnetic induction grid data while determining a local maximum value

结构元能够在该一维磁感应数据中移动，同时判断中心一维结构元中心数据是否大于其两侧数据，若大于，则符合单根载流导体在地表上磁场分布情况，可作为导体位置关键特征点数据进行保存。

在对二维网格化磁感应数据所有列以及行做一维局部最大值判断后，将交叉导体位置关键特征点以及导体位置关键特征点一同作为接地网关键特征点输出即可得到接地网网格拓扑结构。

接地网磁感应数据的二维局部极大值点及一维局部极大值点选取采用算法1，如图8 所示。最终形成一个反映接地网拓扑结构位置信息的数据矩阵，其中有接地网导体的位置数值为1，无接地网导体的位置数值为0。

图8 特征点选取算法Fig.8 Feature point selection algorithm

得到接地网拓扑结构识别结果后，需要对结果进行准确性评价。本文通过计算特征点在真实拓扑结构的置信区间内的比例得出结果的准确性。接地网拓扑结构识别准确性评价采用算法2，如图9 所示。

图9 接地网拓扑结构识别准确性评价算法Fig.9 Accuracy evaluation algorithm for grounding grid structure identification

2 仿真实验

参考相关国家标准GB/T50065—2011《交流电气装置的接地设计规范》[12]，搭建了5×5 均匀网格结构用于实验验证，如图10 所示。确定导体埋地深度为1 m，导体半径为8 mm，仪器检测高度为0.2 m，电流注入点在（3，18）处和（18，3）处，注入大小为5 A的正弦交变电流，频率为1 000 Hz。仿真结果如图11 所示，导出磁感应强度数据。

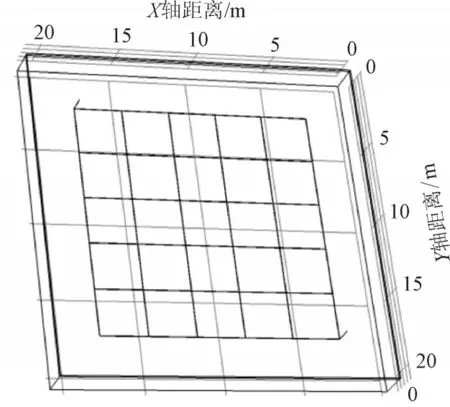
图10 5×5结构的接地网仿真模型搭建Fig.10 Modeling of grounding grid with 5×5 structure

将COMSOL Multiphysics 仿真数据导入MATLAB中进行数据预处理并识别拓扑结构。5×5 结构的接地网磁感应数据插值结果见图12。

图12 5×5结构的接地网磁感应数据插值结果Fig.12 Data interpolation results of magnetic induction in grounding grid with 5×5 structure

通过比较3 种插值结果，可以看出最近邻插值结果有明显锯齿现象，双线性插值结果和双三次插值结果差距不明显。原因是巨大的数据量为线性插值提供支撑，使其结果趋近于双三次插值结果。双三次插值法的效果最好，所以本文后续实验均采用双三次插值结果。

在对数据进行格点插值预处理的基础上，进行5×5 规则接地网拓扑结构的识别，根据导体磁感应数据的特征，构建系统性的数据特征点识别方法。

首先对插值处理后的数据进行二维局部极大值的选取，得到接地网导体交叉点的位置；然后对数据进行一维局部极大值的选取，得到接地网导体的位置，如图13 所示，深绿色圆点标明5×5 规则拓扑结构接地网导体的识别位置，红色线标明了5×5规则拓扑结构接地网的导体的真实位置，准确性结果约为84%，识别效果较好。

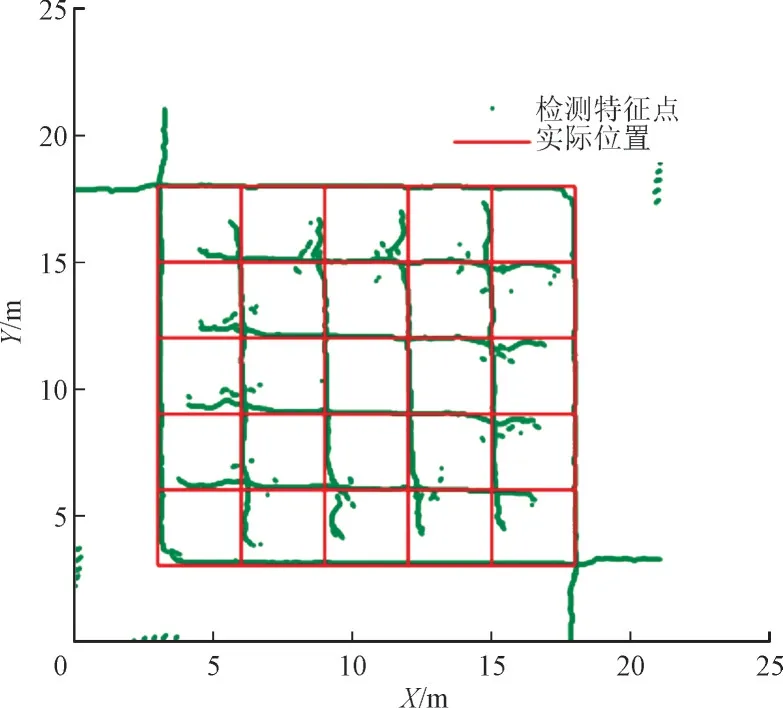
图13 5×5结构接地网拓扑结构识别结果Fig.13 Identification result of grounding grid topology with 5×5 structure

3 实验测试

为验证该方法有效性，本文在某模拟变电站环境的模拟场地搭建了“日”字规则拓扑结构实验平台，该“日”字规则拓扑结构参数如图14 所示。导体埋地深度为1 m，导体半径为8 mm，电流注入点在左上角和右下角两处。

图14 实验模拟接地网拓扑结构参数Fig.14 Parameters for grounding grid topology in experimental simulation

向注入点中注入峰峰值为5 A、频率为1 000 Hz 的正弦交变电流，利用拓扑结构检测仪器进行检测，仪器检测高度为0.2 m，将离散的磁感应数据利用双三次插值法进行插值，得到其磁感应数据分布如图15 所示。

图15 插值处理后磁感应数据Fig.15 Magnetic induction data after interpolation processing

使用接地网拓扑结构识别算法首先同样对插值处理后的数据进行二维局部极大值的选取，得到接地网导体交叉点的位置；然后对数据进行一维局部极大值的选取，得到接地网导体的位置，识别结果如图16 所示，其中深绿色圆点为识别出的接地网导体拓扑结构网格点，红色线表示实际导体拓扑结构布设位置。实验结果表明，针对磁感应数据的关键特征点识别方法，能够大致识别出接地网的拓扑结构，虽然相应地也引入了部分噪声，但识别效果整体较好。

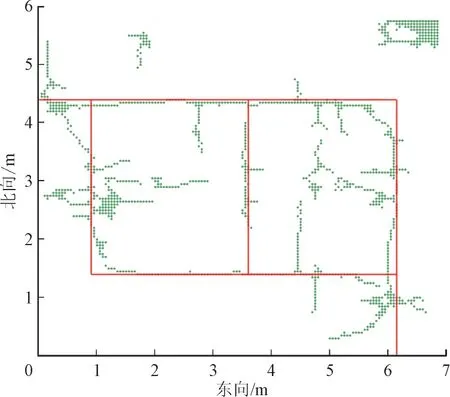
图16 实验识别结果Fig.16 Experimental identification results

4 结论

本文针对接地网磁感应数据存在噪声和采样间隔不均匀的问题，提出了一种规则接地网拓扑结构重建的方法。基于COMSOL Multiphysics 软件搭建仿真模型对方法进行验证，拓扑结构识别的准确率达到了84%，实际实验结果也证实了本文所提拓扑结构重建方法的有效性，可根据含有电磁干扰的磁感应数据重建出实际的接地网拓扑结构，结合接地网布置图纸可以有效地判断接地网的断点，实现接地网故障的智能诊断，具有很好的现实意义。