含频率控制的高比例风电经LCC-HVDC外送系统的机电稳定性分析

方 正，汤瑞阳，何青青，何珍玉，肖厦颖，范传光

（1.武汉理工大学自动化学院，湖北武汉 430070；2.国网孝感供电公司，湖北孝感 432000；3.湖北省电力规划设计研究院有限公司，湖北武汉 430070）

0 引言

随着人类大规模采用化石能源引发温室效应，从而导致全球气候变暖[1]，全球各地开始积极发展新能源以取代传统化石能源，其中风能作为一种可再生的清洁能源引起了广泛重视[2]。截至2023 年一季度末，全国风电累计装机达到3.76×108kW，同比增长11.8%，其中陆上风电3.45×108kW，海上风电3.089×107kW[3]。由于我国风能资源丰富的地区大多距离用电负荷中心较远[4]，因此大规模风电并网对外输送电能成为目前需要攻克的难题。而高压直流输电（High-voltage Direct Current，HVDC）因其传送容量大、线路损耗低、稳定性高、功率调节快速灵活[5]，是将风电向外输送的主流解决方案。然而，长距离、重负荷的直流输电通道会使电力系统惯量降低、频率动态恶化，对电网的安全平稳运行造成严重威胁[6]。

引入双馈风机（Doubly-fed Induction Generator，DFIG）的频率控制，主动支撑系统频率动态，是解决问题的有效措施。DFIG 的频率控制包含惯量控制和一次调频2 个环节：一方面可以通过引入不同的双馈风机惯量控制策略[7-8]，为电网提供持续的频率支撑，改善电网频率的暂态稳定性；另一方面基于DFIG 的灵活可控特点，可以设计出多样的一次调频控制方案，使DFIG 具备一次调频响应能力[9-11]。类似地，HVDC 系统也加入了频率限制控制（Frequency Limit Control，FLC）环节来改善互联系统频率动态稳定，实现了直流功率大范围快速调节，从而提高了电网频率稳定性[12-14]。

然而，由于风电机组的转动惯量时间常数和同步机组接近，风机/直流等频率控制的时间尺度与同步机组摇摆模态时间尺度接近，相应引入的频率控制模态可能会对系统机电时间尺度的动态特性产生影响。针对风电经直流外送系统的机电稳定性问题，文献[15]研究了风电接入大电网经直流外送系统的电压稳定性，得出了在满足电压稳定性的情况下风电渗透率的上限。文献[16]在弱电网与传统HVDC 和DFIG 互联系统中，研究了交流系统的机电模式和高压直流锁相环模式分别对惯性和有效短路比的影响。文献[17]进一步分析了在DFIG 和HVDC 与外部大电网相连的系统中DFIG 直流电压、端电压、锁相环和直流系统整流侧定电流控制、锁相环之间的相互影响。文献[18]研究了风电接入交直流混联系统的稳定性问题，分析了DFIG 惯量控制和直流FLC 对系统区间低频振荡的影响。可见当前对风电经直流外送系统机电时间尺度振荡问题的研究很少，所分析的频率控制策略还不够全面，相应控制策略下的控制参数以及其他控制环之间的相互作用对系统机电时间尺度振荡的影响缺少必要的论证。因此，研究和分析风电和直流输电频率控制对送端电网机电时间尺度振荡的影响在工程应用中具有很强的实际意义。

为此，本文从风电和直流输电不同控制策略和控制参数着手，主要分析风电频率控制和直流FLC对送端系统机电时间尺度振荡的影响。搭建了含双馈风机的两区四机经传统直流外送系统的数学和时域模型，其中双馈风机加入了惯量控制及一次调频控制，直流输电系统引入了FLC 环节，基于该典型场景研究送端风电机组及直流换流站等电力电子装备频率控制对系统机电时间尺度振荡的影响。

1 双馈风机经直流外送系统建模

1.1 双馈风机整体拓扑结构

双馈风机经直流外送系统的整体拓扑如图1 所示，该系统存在2 个区域，包含2 台同步机（Synchronous Generator，SG）。在节点6 接入风电场，相应减少同步机SG2 的发电量以保持潮流不变，并通过相控换流器高压直流输电系统（Line-Commutated Converter HVDC，LCC-HVDC）对受端交流电网供电。

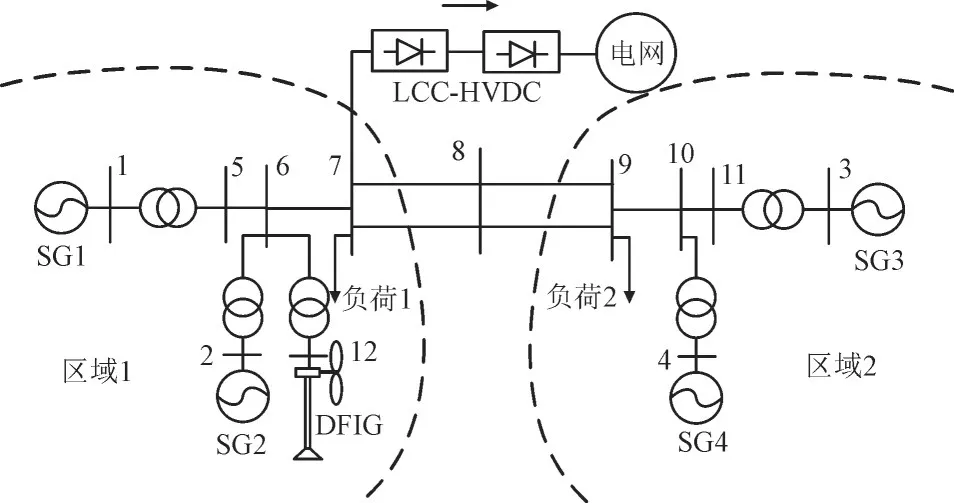
图1 双馈风机经直流外送系统的拓扑结构Fig.1 Topology of sending system through LCC-HVDC with DFIG

1.2 双馈风机附加频率控制建模

1.2.1 DFIG惯量控制建模

目前主要的DFIG 惯量控制方法有2 种：（1）根据电网电压频率变化率（df/dt），通过引入反馈支路调节转子侧的电磁转矩和有功电流参考值[19]；（2）采取虚拟同步机控制策略，使DFIG 功率控制环节模拟同步发电机的转子运动方程[20]。由于后者需要大幅改变原有的矢量控制结构，因此本文使用第1 种方法，其控制结构如图2 所示。考虑到微分环节易引入高频信号，因此需进行低通滤波。图2 中，Kf为微分环节的增益系数，Tf为低通滤波环节的时间常数，θt为DFIG 端电压相位，ω0为DFIG 额定转速，ωPLL，fPLL分别为锁相环输出的角速度与频率，Tadd为DFIG 惯量控制附加的转矩。

图2 双馈风机惯量控制结构图Fig.2 Structure of inertia control for DFIG

DFIG 的转子动能Ek为：

式中：J为转动惯量；ωr为DFIG 转子转速。

当系统频率变化后，DFIG 转子释放能量ΔE为：

DFIG 的惯性时间常数H为：

式中：SN为DFIG 额定容量；ω0为工频频率。

联立式（2）和式（3）可得：

对式（4）进行标幺化，标幺化下ω=f。由于ωr与ω0偏差很小，因此标幺化下可将ωr近似为1，可得：

当df/dt＞0，ΔE＞0，DFIG 转子释放动能，转速降低，Tadd＜0，电磁转矩减小，转子电流减小；当df/dt＜0，ΔE＜0，DFIG 转子存储动能，转速增大，Tadd＞0，电磁转矩增大，转子电流增大。其基本思路是根据电网电压频率的变化率（df/dt）调节电磁转矩，从而实现对风电机组的频率模态支撑。

1.2.2 DFIG桨距角减载一次调频

本文采用如图3 所示的桨距角减载调频控制模式，图中Pmax为有功功率最大值。在风速v1下，当DFIG 最大功率曲线系数不变时，桨距角从β1减小至β0，DFIG 的稳定运行点可由B点移动至A点，从而使有功功率增加ΔP1。而将桨距角从β1增加至β2，则可使DFIG 稳定运行点由B点移动至C点，导致有功功率减少ΔP2。

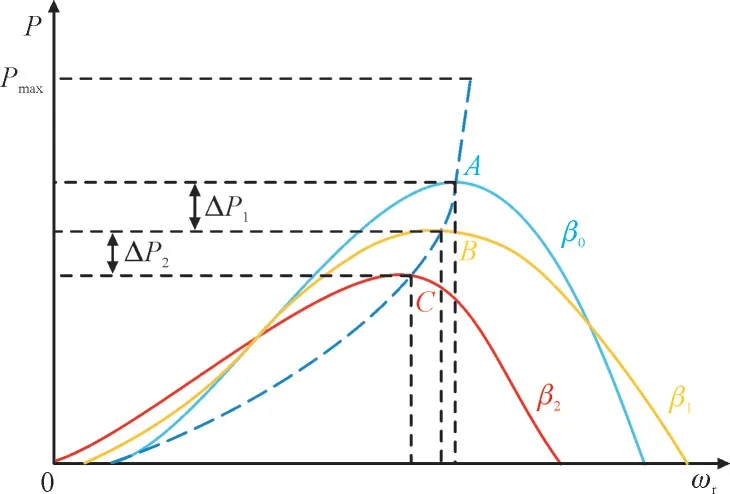
图3 桨距角减载曲线Fig.3 Curves for pitch angle load shedding

首先给定减载率d%，DFIG 输出功率为Pmeas，则减载后的有功功率Pr参考值为：

采用频率-有功下垂控制对桨距角进行调节，则有功偏差ΔPw为：

式中：K为下垂控制系数；fN为基准频率。

故桨距角减载一次调频的有功参考值Pref为：

由此可得一次调频控制框图如图4 所示。其中，Vw为风速，ωref为在DFIG 转速指定值，Lm为定、转子等效绕组之间的互感，Ls为定子等效绕组的自感，ψs为定子磁链矢量，Tew为电磁转矩，Tadd为惯量控制附加的转矩，Te*为电磁转矩指令值，ird*为转子电流d轴分量指令值，kp为桨距角控制比例系数。

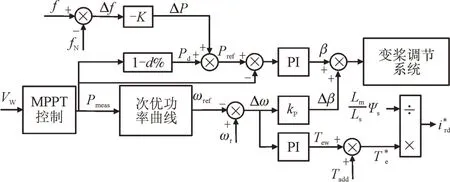
图4 桨距角减载一次调频控制框图Fig.4 Block diagram of pitch angle load shedding primary frequency control

1.3 直流外送系统基本控制策略

本文采用如图5 所示的直流外送系统，其中整流侧和逆变侧分别采用定电流和定电压控制。在传统HVDC 系统基础上，为了实现直流传输功率的可调性以满足对电网频率的动态调节，需要在直流系统的送端换流站加入FLC。

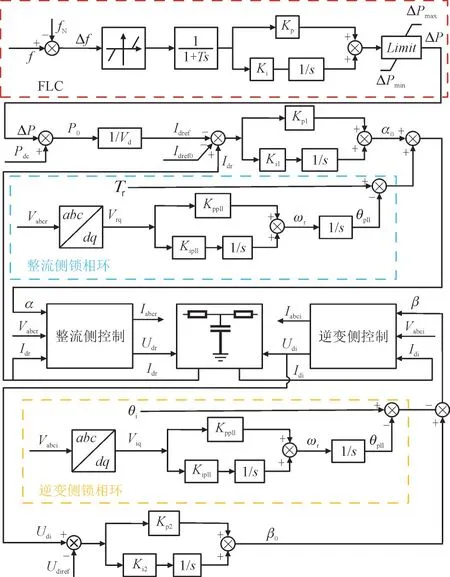
图5 直流外送系统控制框图Fig.5 Control block diagram for DC transmission system

图5 中，Vabcr，Iabcr分别为整流侧三相交流电压和电流，Idr为直流线路电流，α，α0分别为触发延迟角的参考值和初始值，β，β0分别为触发超前角的参考值和初始值，Udr，Vd，Pdc，θr分别为整流侧的直流电压、直流电压幅值、直流输电功率和端电压相位，Vabci，Iabci为逆变侧三相交流电压和电流，Udi，Idi，θi分别为逆变侧的直流电压、线路电流和端电压相位，Udiref为逆变侧的直流电压参考值，Idref，Idref0为直流输电线路电流参考值和初始电流参考值，P0为直流输电功率参考值，ΔP为FLC 的输出，ΔPmax，ΔPmin为输出上下限，Kp，Ki为FLC 比例和积分系数，T为惯性时间常数，Kp1，Ki1为整流侧电流控制器比例和积分系数，Kp2，Ki2为逆变侧电压控制器比例和积分系数，Kppll，Kipll为锁相环比例和积分系数，θpll为锁相环输出的角度。

由图5 可知，当系统频率与基准频率的偏差值高于FLC 死区设定的上下限时，FLC 开始调节直流传输功率。以频率偏差高于FLC 设定的死区上限为例，FLC 的控制原理为：

式中：fh为FLC 死区上限。

当系统频率偏差Δf-fh＞0 时，ΔP增大，P0增大；当Δf-fh＜0 时，ΔP减小至0，P0减小。

2 风机附加频率控制对系统机电时间尺度振荡的影响

为了分析DFIG 附加频率控制对系统机电时间尺度振荡的影响机理，本文将两区四机系统简化为两机系统，采用简化系统进行初步理论分析，如图6所示。其中，X1，X2，X3为各机组到母线的等效电抗，E'为同步发电机SG1 的内电势幅值，UG为DFIG 并网点电压幅值，U为平衡机SG2 的端电压幅值，δ1为SG1 内电势相角，θ为SG1 内电势与SG2 端电压相角差，Pline为输电线路传输有功功率，PSG1和PDFIG分别为SG1 和DFIG 输出有功功率。

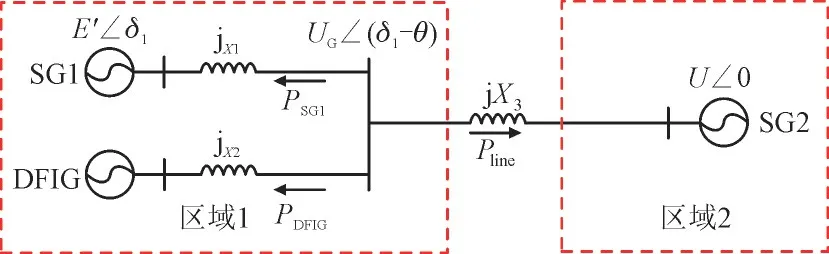
图6 DFIG接入两机系统结构图Fig.6 Structure diagram of two-machine system with DFIG

机电时间尺度振荡过程中，系统总能量波动来源于同步机及DFIG，因此，同步发电机SG1 的摇摆方程在平衡点处线性化后可表示为[21]：

式中：ΔPSG1为SG1 的有功功率变化量；HSG1为同步发电机SG1 的惯性时间常数；DSG1为SG1 的阻尼系数；Δδ1为SG1 的功角变化量。

在两机系统中进行低频振荡试验时，一般采用同步发电机SG2 的并网点（Point of Common Coupling，PCC）为参考节点，即：同步发电机SG2 的参考节点电压保持恒定；不考虑风速改变，DFIG 输出功率恒定；采用相应的无功补偿措施，保持PCC 电压UG的值不变。SG1 输出有功变化量ΔPSG1为：

式中：θ0为θ的初始值，Δθ=θ-θ0。

可近似将SG1 的电角速度看作为PLL 输出的角速度，由图6 可得DFIG 输出有功变化量ΔP为：

两区域联络线输送的有功变化量ΔPline可表示为：

式中：δ0为δ的初始值。

SG1 输出有功功率变化量ΔPSG1的表达式为：

将式（11）—式（13）代入式（14）中可得：

由式（15）可得SG1 的功角摇摆方程表达式为：

其中，

因此，引入DFIG 的惯量控制可以提高电力系统的整体惯量，有利于响应系统频率的动态变化。

由数学模型计算得到不加频率控制的系统特征根和参与因子如表1 所示，其中Δωi，Δδi（i=1，2，3，4）为与同步机相关的状态变量，Δωw，ΔTw为与风机相关的状态变量。

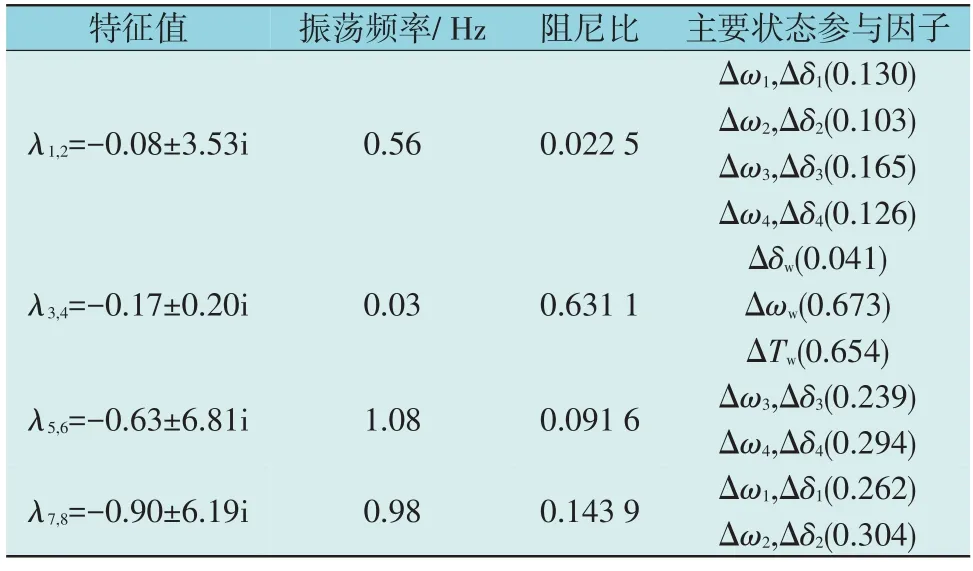
表1 不含频率控制的系统特征值与参与因子Table 1 Eigenvalues and participation factors of system without frequency control

从表1 可以看出，两区四机经直流外送系统机电时间尺度振荡模式主要涉及到同步发电机组的转速和转子角度。第1 组特征根的实部最大，最靠近虚轴，因此是系统的主导特征根，说明系统的主导振荡模式为区间振荡；第2 组特征根为风机接入该系统的特征根，具体体现在区域1、区域2 之间联络线上的功率振荡。

对双馈风机附加惯量控制，其惯量控制增益Kf=30，滤波时间常数Tf=0.5。采用特征值分析法得到系统特征根及状态变量参与因子如表2 所示。

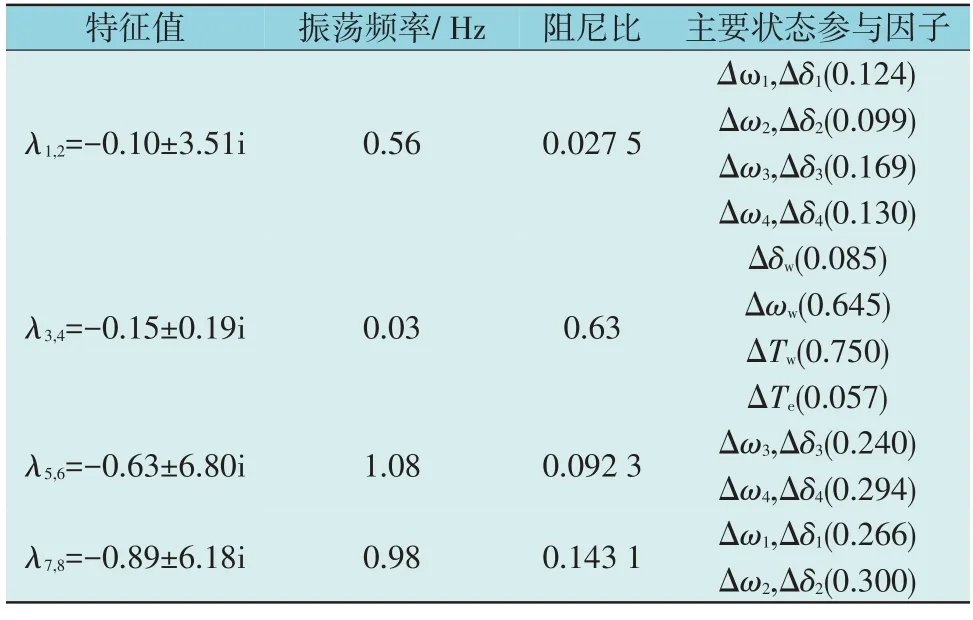
表2 DFIG加入惯量控制后的系统特征值与参与因子Table 2 Eigenvalues and participation factors of system with inertial control of DFIG

对比表2、表1 可得，风机加入惯量控制后系统区间振荡模态的阻尼比增大了，主导特征根实部减小。由此可知，加入惯量控制能够给系统提供正阻尼，抑制区间机电时间尺度振荡。

为了更清楚地揭示惯量控制对风电经直流外送系统阻尼特性的影响，本文进行了如下工作：（1）保持风机惯量控制增益Kf=30 不变，改变滤波时间常数Tf；（2）保持Tf=2 不变，改变Kf。由此可得不同惯量控制参数下两区四机系统区域间振荡模式的特征根轨迹和阻尼模态变化如图7 所示。

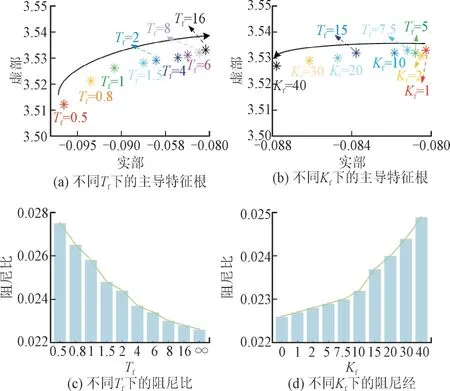
图7 DFIG加入惯量控制对系统机电稳定性的影响Fig.7 Impact of DFIG with inertial control on electromechanical stability of system

图7（a）显示了风机惯量控制滤波时间常数Tf从0.5 增大到16 时的特征根轨迹，可见Tf增大时，区间振荡主导特征根的会向右移动。由图7（c）可知，随着Tf增大，系统区间振荡模态阻尼比减小，对机电时间尺度振荡的抑制效果变差；图7（b）显示了风机惯量控制增益Kf从0 增大到40 时的特征根轨迹，可见Kf增大时，区间振荡主导特征根会向左移动。由图7（d）可知，适当增大风机惯量控制参数增益Kf时，系统区间振荡模态阻尼比增大，对机电时间尺度振荡的抑制效果变好。因此，选择合适的惯量控制滤波时间常数Tf和增益Kf可以有效增大系统的稳定性。

3 直流频率限制控制对系统机电时间尺度振荡的影响

为了分析直流FLC 对系统机电时间尺度振荡的影响，本文对两区四机经LCC-HVDC 外送系统进行简化，将4 台同步发电机和1 组风机替代为1 台同步机，并经过HVDC 系统对无穷大电网进行功率传输，采用两机系统进行初步的理论分析，如图8所示。其中，Pe为SG 的电磁功率，Pd为HVDC 传输有功功率，XΣ为SG 等值电抗，δ为SG 转子角度。

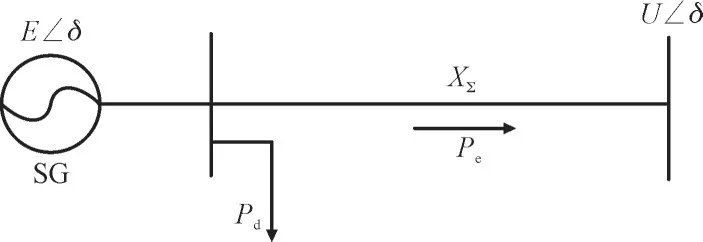
图8 两机系统模型Fig.8 Two-machine system model

对于无调速器、无稳定器的同步发电机SG 而言，不考虑同步机的阻尼作用，即阻尼系数DSG=0，则两机系统的功率方程可表示为：

式中：Pm同步发电机SG 的机械功率；Tj为SG 转动惯量。

对式（18）进行线性化可得：

式中：Δ 为变化量。

由于SG 输出的有功参考值恒定不变，故可设定SG 的机械功率不变，即ΔPm=0。

SG 电磁功率的变化量ΔPe为：

则式（19）进一步可改写为：

当直流输电附加FLC 后，则有：

式（23）中，可以假定系统频率的变化量等价于SG 转子转速的变化量，即：

则式（23）可改写为：

将式（25）代入式（22）中可得：

对应微分方程的特征根为：

加入直流FLC 后，需要选择合适的Kp参数使微分方程的特征根λ1，2＜0，即系统具有正阻尼系数。由于Kp为正数，即微分方程2 个根均在复平面的左侧，即转子角度的振荡将随着时间衰减。因此，对于直流FLC，可以理解为：当系统有功功率发生机电时间尺度振荡时，由于直流FLC 能够跟随系统频率的变化量Δf调节直流外送传输的有功功率，能够对频率的波动进行抑制，使其稳定在额定频率，能够为系统提供正阻尼，抑制系统机电时间尺度振荡，使系统的稳定性增强。

为了更好地揭示FLC 对系统机电时间尺度振荡的影响，取消风机的惯量控制和一次调频，仅存在直流FLC 调节系统频率，计算得到的系统特征根及主要参与状态如表3 所示。其中Δωi，Δδi（i=1，2，3，4）为与同步机相关的状态变量，Δωw，ΔTw为与风机相关的状态变量。

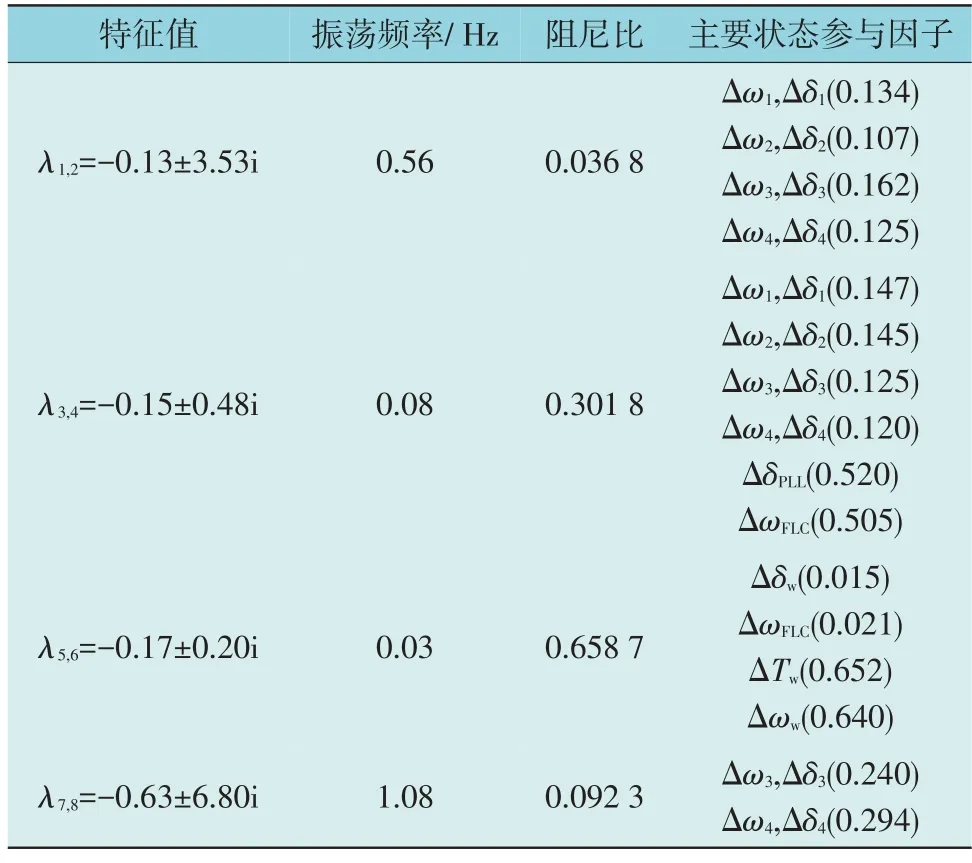
表3 直流输电加入FLC的系统特征值与主要状态参与因子Table 3 Eigenvalues and participation factors of system with FLC of DC transmission

由表3 可知系统加入直流FLC 后，区间振荡的阻尼比增大了，主导特征根向左移动。由此可知，加入FLC 能够给系统提供正阻尼，抑制区间机电时间尺度振荡。由第2 组特征根λ3，4可以得出，直流FLC 的参与程度和整流侧锁相环角度变化量ΔδPLL的参与程度较大，因此，有必要对直流FLC 的带宽和直流送端换流站锁相环带宽进行分析。分别改变直流FLC 带宽和直流换流站锁相环带宽，可得区域间振荡模式特征根轨迹和阻尼模态变化如图9 所示。

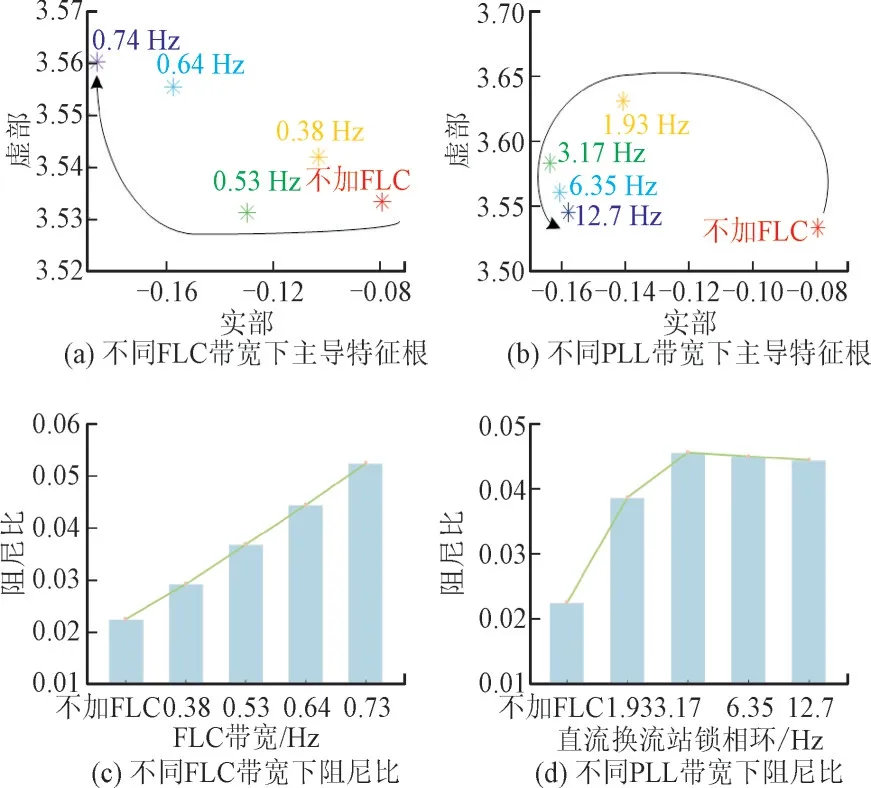
图9 直流FLC对系统机电稳定性的影响Fig.9 Impact of DC FLC on electromechanical stability of system

图9（a）显示了FLC 带宽从0.38 Hz 变化到0.74 Hz 时的主导特征根轨迹，可见随着直流FLC带宽的增加，区间振荡主导特征根向左移动，对应于图9（c）系统区间振荡模态阻尼比增大；图9（b）显示了不同直流换流站锁相环带宽下的区间振荡模式特征根轨迹，可见随着带宽的增大，系统的区间振荡主导特征根先向左移动，后稍微向右移动，对应图9（d）系统区间振荡模态阻尼比先增大后减小。

4 时域仿真验证

为了验证第3 章理论分析的正确性，本文搭建了图1 拓扑结构的两区四机经LCC-HVDC 外送系统时域仿真模型，并且进行了与特征值分析相同的实验。通过设置功率扰动，观测直流外送系统传输功率的响应波形振荡幅值，由此评估系统的稳定性。仿真结果如图10 和图11 所示。

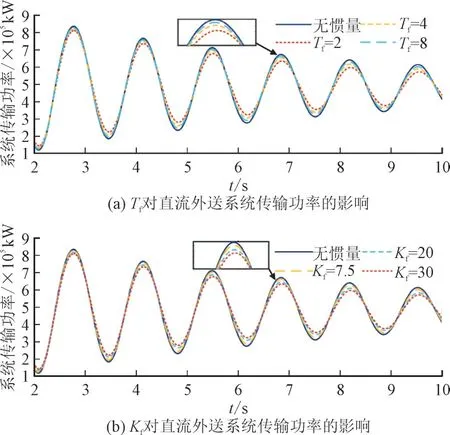
图10 DFIG加入惯量控制对直流外送系统传输功率的影响Fig.10 Impact of DFIG with inertial control on transmission power of DC transmission system

图11 直流FLC对直流外送系统传输功率的影响Fig.11 Influence of DC FLC on transmission power of DC transmission system

图10 显示了不同惯量控制参数下的直流外送系统传输功率波形，可见当双馈风机附加惯量控制后，直流外送系统传输功率振荡幅值减小。由图10（a）可知，增大风机惯量控制滤波时间常数Tf，直流外送系统传输功率的振荡幅值增大，即系统区间振荡模态阻尼比减小；由图10（b）可知，增大风机惯量控制参数增益Kf时，直流外送系统传输功率的振荡幅值减小，即系统区间振荡模态阻尼比增大，与图7 特征值分析得出的结论相符合。

图11（a）显示了不同FLC 带宽下的直流外送系统传输功率波形，可见加入直流FLC 能够减小区间机电时间尺度振荡幅值，抑制区间机电时间尺度振荡，随着FLC 带宽由0.38 Hz 增大到0.74 Hz 后，直流外送系统传输功率幅值逐渐降低；图11（b）显示了不同直流换流站锁相环带宽下的直流外送系统传输功率波形，可见随着直流送端换流站锁相环带宽的增大，直流外送系统传输功率的机电时间尺度振荡幅值先减小后稍微增大，与图9 的特征值分析结果一致。

5 结论

本文建立了含频率控制的双馈风机经LCCHVDC 外送系统的机电时间尺度稳定性分析模型，研究了风电经LCC-HVDC 外送系统中风机/直流等频率控制对送端电网机电时间尺度振荡的影响，主要得出以下结论：

1）风机附加惯量控制后，能够增大系统区间振荡模态阻尼比。减小惯量控制滤波时间常数和增大惯量控制参数增益均能一定程度提高系统区间振荡模态阻尼比。

2）直流FLC 带宽及送端换流站锁相环对系统区间振荡模态阻尼比的影响较大。在一定范围内，随着直流FLC 的带宽增大，系统区间振荡模态阻尼比增大，机电稳定性增强；增大直流送端换流站锁相环带宽，系统区间振荡模态阻尼比先增大后减小。