基于CDAE和TCN/BLSTM模型的电能质量扰动分类方法

代义东，陆之洋，熊 炜，袁旭峰，徐玉韬，谈竹奎

（1.贵州大学电气工程学院，贵州贵阳 550025；2.贵州电网有限责任公司电力科学研究院，贵州贵阳 550002）

0 引言

随着“碳达峰、碳中和”目标的提出，新能源的发展已走上快车道，以光伏、风电为代表的新能源在电网中不断渗透，导致新型电力系统的源荷发生很大变化[1]。新能源出力的随机性和波动性会带来严重的电能质量扰动（Power Quality Disturbances，PQDs）问题，进而威胁到电网的稳定运行[2]。因此，快速、高效且准确地对PQDs 进行分类是保障电网稳定运行的前提[3]。

以往的研究中PQDs 分类有信号分析、特征选取和扰动分类3 个步骤。信号分析主要采用傅里叶变换[4]、小波变换[5]、S 变换[6]和模态分解[7]等方法，以此得到时频域特征。经过人工选取特征集后，再利用决策数[8]、支持向量机[9]等分类器完成分类。传统方法虽然取得不错的分类效果，但严重依赖专家经验，限制了扰动的最佳特征提取，且分类的类别有限。随着扰动的复杂化，传统方法已难以满足电网对PQDs 的分类需求。

为解决传统方法的不足，在PQDs 分类中引入了深度学习[10]。深度学习具有优秀的自训练和特征提取能力，其描述的深度特征能够充分识别扰动类别。目前，深度学习在分类领域主要从以下两方面切入：（1）是将扰动信号通过二维映射[11]、可视化轨迹圆[12]、格拉姆角场[13]等转化为图像，再利用卷积神经网络（Convolutional Neural Network，CNN）提取特征并完成分类，但图像化过程繁琐且会导致扰动特征丢失；（2）是直接将PQDs 作为分类对象，利用一维卷积[14]、稀疏自动编码器[15]、注意力机制[16]及门控循环单元[17]提取PQDs 的抽象、时序特征，或通过串行设计的卷积-长短期记忆[18]或全卷积-长短期记忆[19]等学习特征间的关联性，完成PQDs 的分类。相比之下，根据PQDs 的时序特性进行分类不仅无需任何转换且能够加快处理流程，更有利于后续的实时监测和定位。目前，在此类研究中主要使用卷积神经网络、循环神经网络或2 者的串行模型来实现对PQDs 的分类。其中，卷积神经网络的缺点是缺乏时序相关性，循环神经网络的缺点是缺乏长期依赖性，串行模型的缺点是容易陷入局部最优而无法达到全局最优。这3 种方法不仅会导致扰动的时序特性被扰乱，而且会造成网络过深引起的梯度爆炸和过拟合等问题。同时，在实际环境中，噪声也会掩盖PQDs 的固有特征，导致分类模型难以提取有效信息，进而降低其分类性能。因此，有必要针对随机噪声下的扰动，设计一种抗噪性能强、兼顾抽象和时序特征的分类方法。

综上所述，本文将卷积降噪自编码器（Convolutional Denoising Auto-encoder，CDAE）、时域卷积网络（Temporal Convolutional Network，TCN）和双向长短期记忆（BidirectionalLongShort-termMemory，BLSTM）相结合，提出基于CDAE 和TCN/BLSTM 模型的PQDs 分类方法。研究的创新之处在于：（1）考虑了实际环境中噪声对PQDs 的影响，通过CDAE 对含噪信号进行重构，进而获取不含噪声的信号；（2）以并行模式搭建TCN/BLSTM，挖掘抽象特征和时序特征的深度信息，并运用批量归一化（Batch Normalization，BN）加速模型收敛，使模型具有更好的分类性能。

1 CDAE和TCN/BLSTM分类模型

为实现对噪声环境下的PQDs 分类，本文设计的CDAE 和TCN/BLSTM 分类模型如图1 所示。其中，第一部分为CDAE 模型，主要实现降噪处理；第二部分为TCN/BLSTM 模型，主要实现特征提取；第三部分为特征合并（Features Merging，FM）模型，主要实现特征融合和分类。

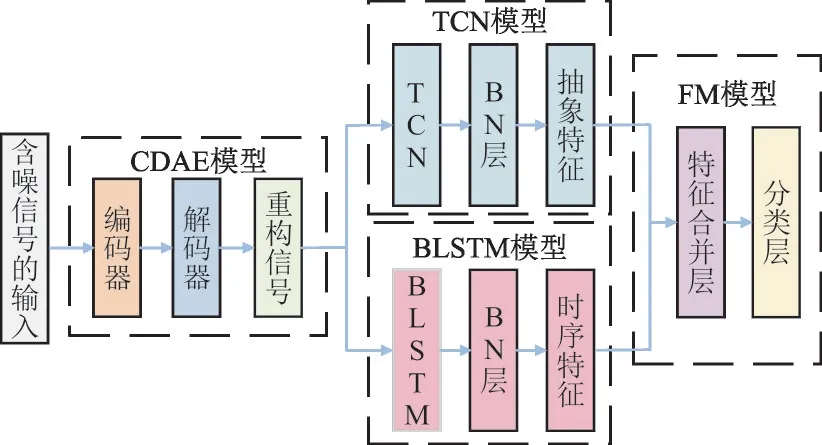
图1 CDAE和TCN/BLSTM分类模型Fig.1 CDAE and TCN/BLSTM classification model

1.1 CDAE模型

CDAE 通过卷积、池化、反卷积和上采样替代降噪自编码器（Denoising Auto-encoder，DAE）的全连接。连接方式的改变不仅降低了网络复杂性，而且避免了参数糅杂[20]。在CDAE 中，由卷积和池化构成编码器用于特征学习并对特征进行降维，反卷积和上采样构成解码器用于重构信号并对特征进行还原，CDAE 模型的降噪过程如图2 所示。

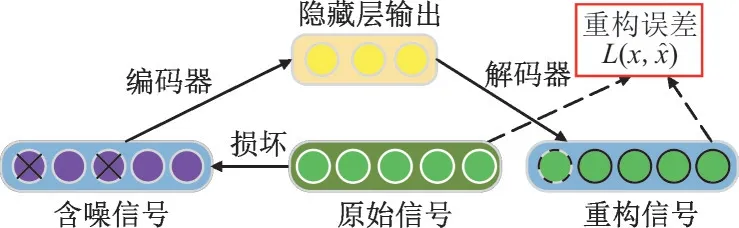
图2 CDAE模型的降噪过程Fig.2 Noise reduction process of CDAE model

CDAE 模型对第i个含噪信号的降噪过程表达式为：

式中：W1，B1分别为编码器权重和偏置；W2，B2分别为解码器权重和偏置；f为Relu 激活函数；θ为CDAE 的相关参数；n为含噪信号的总量。

1.2 TCN模型

TCN 以全卷积神经网络（Fully Convolutional Networks，FCN）为基础，利用因果、扩张卷积层替代传统卷积，其中因果卷积使其能充分进行序列学习，扩张卷积使其具有充足的感受野，从而拟合更多的信息，TCN 较全卷积神经网络更加适合处理时序问题[21]。TCN 的因果扩张卷积结构如图3 所示。其中，分别为0 时刻到t时刻输入的重构信号，d为扩张系数（每层的扩张系数随着模型深度加深呈现指数性增大），yt为t时刻的因果扩张卷积特征。

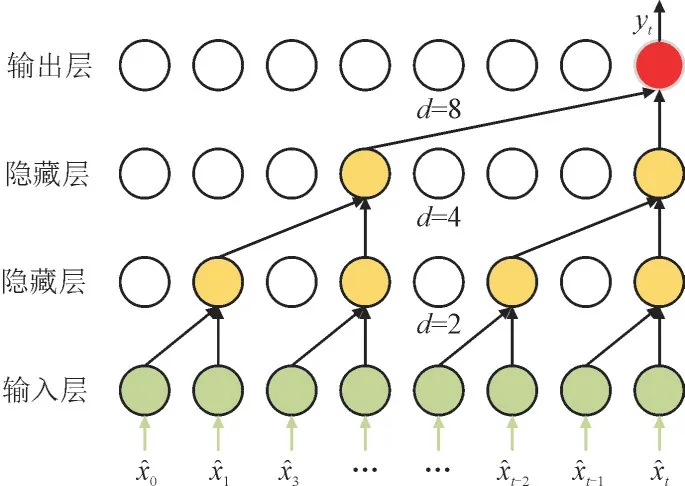
图3 TCN的因果扩张卷积结构Fig.3 Causal expansion convolution structure of TCN

TCN 模型由残差块和BN 层组成，其模型结构如图4 所示。其中，为t时刻的yt经过BN 层优化后得到的抽象特征。

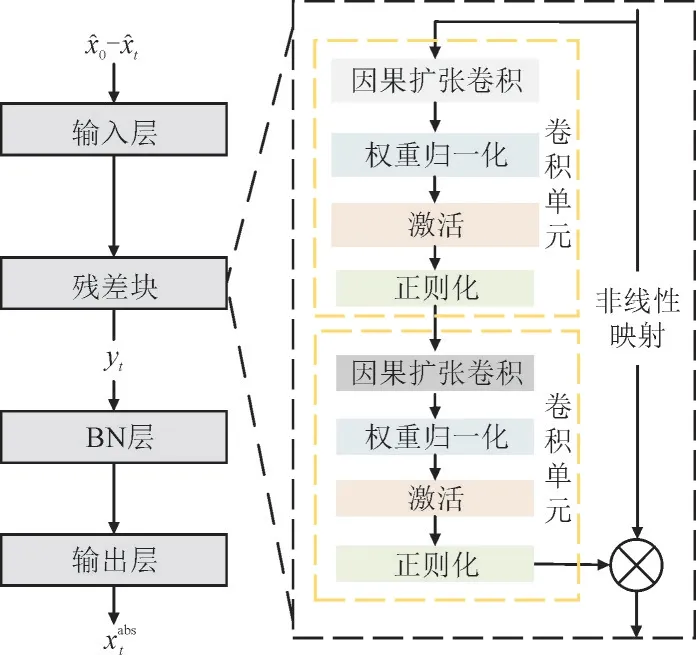
图4 TCN模型结构Fig.4 Structure of TCN model

由图4 可知，残差块中包含2 个卷积单元和非线性映射，卷积单元可以充分提取抽象特征的深度信息，非线性映射则可以保证输入和输出具有相同的维度。BN 层可以提高训练速度，而且能对数据进行标准化处理，从而保持相同分布。

TCN 模型对t时刻的因果扩张卷积特征进行BN 优化后，得到的抽象特征表达式为：

式中：μ，φ2分别为yt的期望和方差；γ，β为可学习参数；ε为随机正值。

1.3 BLSTM模型

BLSTM 模型可对长短不一的序列进行学习，且能学习正反向序列的关联关系，使模型在更细粒度的分类问题上更具优势[22]。本文中的BLSTM 模型由长短期记忆（Long Short-term Memory，LSTM）和BN 组成，其模型结构如图5 所示。其中，分别为t-1 时刻到t+1 时刻输入的重构信号，ht，分别为t时刻的正向隐层状态、反向隐层状态，ht-1，ht+1和分别为t-1，t+1 时刻的正向隐层状态、反向隐层状态，w1，w3分别为正向隐层、反向隐层与输入层间的权重，w2，w4为为正向隐层间、反向隐层间的权重，w5，w6分别为正向隐层、反向隐层和输出层间的权重，为t时刻的时序特征。

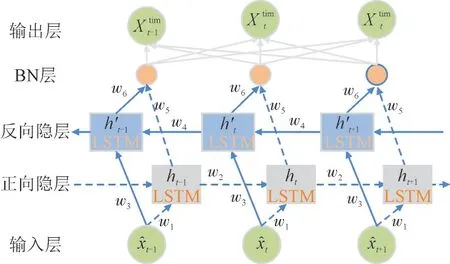
图5 BLSTM模型结构Fig.5 Structure of BLSTM model

BLSTM 模型对t时刻的ht和进行BN 层优化后，得到的时序特征表达式为：

1.4 FM模型

FM 模型的特征合并层将抽象特征Xabs和时序特征Xtim进行融合，其表达式为：

式中：concat 为融合过程函数；Xfus为融合特征。

采用Softmax 激活函数对分类层进行激活，其值表示输入样本被正确分类的概率，其表达式为：

2 模型搭建和训练方法

为测试模型的有效性，计算机的CPU 和RAM分别为Intel（R）i7-9750H 和16.0 GB，PQDs 数据集由Matlab2018b 仿真生成。分类模型在基于Python语言的Keras 框架上进行搭建，开发软件为Pycharm，分类模型的架构参数如表1 所示。表1中，Input1/2 为输入层，Conv1/2 为卷积层，Mp1/2 为池化层，Dconv1/2 为反卷积层，Us1/2 为上采样层，TCN 为时域卷积层，BLSTM 为长短期记忆层，BN1/2为归一化层，Concatenate 为特征合并层，全连接（Fully Connected，FC）为全连接层，Output 为输出层，q为过滤器个数，k为内核个数，p为池大小，units 为神经元个数。

表1 分类模型的架构参数Table 1 Architectural parameters of classification model

将CDAE 和TCN/BLSTM 的批大小分别设为128 个和64 个，迭代次数分别设为500 次和60 次，初始学习率分别设为0.3%和0.25%，优化器均选用Nadam。采用均方误差（Mean Squared Error，MSE）训练CDAE 模型，采用分类交叉熵（Classification Cross Entropy，CCE）训练TCN/BLSTM 模型，均方误差损失LMSE和分类交叉熵损失LCCE的表达式为：

3 仿真分析

3.1 PQDs数据集

根据IEEE Std 1159—2019 和文献[23]的PQDs数学模型，由Matlab 仿真20 类PQDs 信号进行测试：正常（C1）、暂降（C2）、暂升（C3）、中断（C4）、脉冲（C5）、振荡（C6）、谐波（C7）、闪变（C8）、暂降/升+谐波（C9，C10）、暂降/升+闪变（C11，C12）、暂降/升+振荡（C13，C14）、暂降/升+谐波+闪变（C15，C16），暂降/升+谐波+振荡（C17，C18），暂降/升+谐波+振荡+闪变（C19，C20）。其中包含8 类单一扰动，12类复合扰动。基频设为50 Hz，采样频率设为3 200 Hz，采样长度设为10 个周期，共计640 个采样点。每类扰动采集2 000 个样本，共计40 000 个样本。实时PQDs 采集时会存在噪声，主要以高斯白噪声为主[24-25]。因此，添加信噪比为20～40 dB 的高斯白噪声，并按照8∶1∶1 比例划分训练集、验证集和测试集。其中，验证集设定是为了监测验证损失和精度，进而保存最优模型[26]。为对模型进行比较，额外采集信噪比为20 dB，30 dB，40 dB 和（20+30+40）dB的测试集。为适应不同电压幅值，对PQDs 信号均进行归一化处理。由于复合扰动为单一扰动的不同叠加组合，因此仅展示单一扰动的波形如图6 所示。

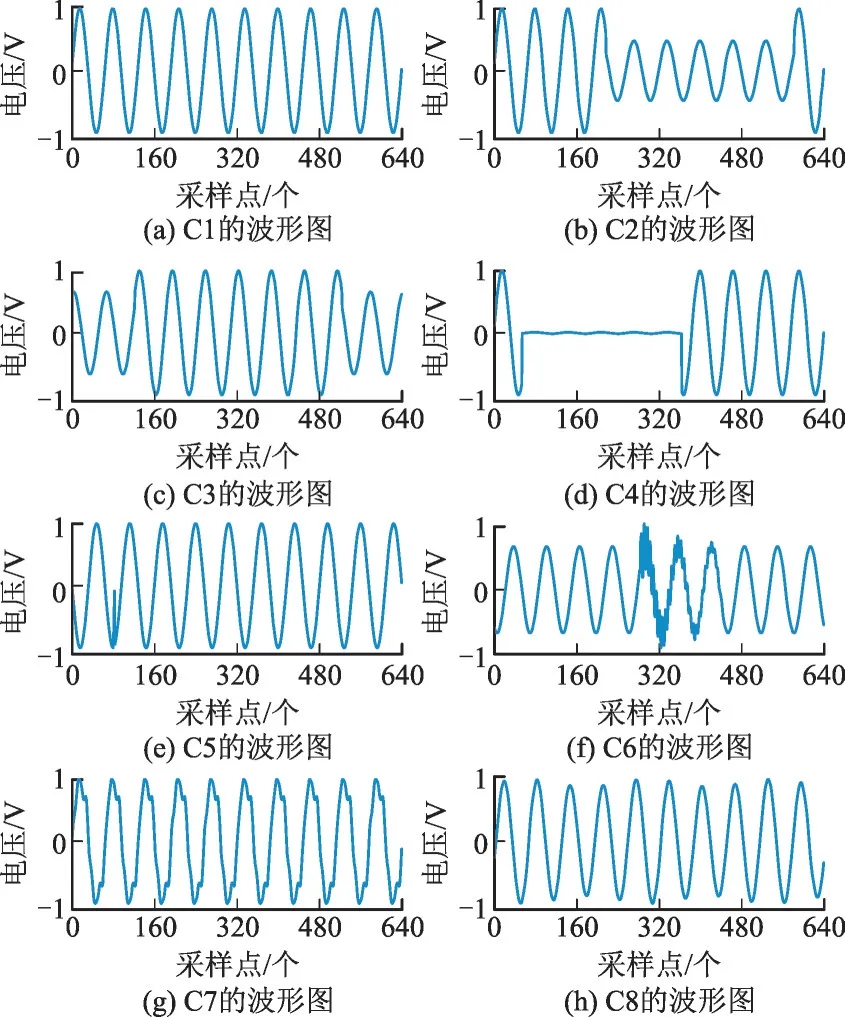
图6 单一扰动的波形图Fig.6 Waveforms of single disturbance

3.2 模型训练

在CDAE 和TCN/BLSTM 的训练过程中，学习率过大会导致无法收敛到最小值，学习率过小会导致收敛缓慢[27]。因此，引入衰减策略对学习率进行动态调整，以提升模型的精度和性能[28]。CDAE 的训练过程如图7 所示。

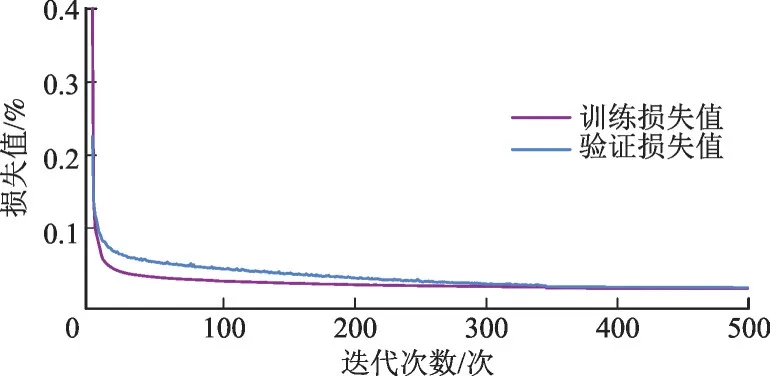
图7 CDAE的训练过程Fig.7 Training process of CDAE

由图7 可知，随着迭代次数的增加，训练损失和验证损失不断趋于重合，说明重构信号和原始信号也趋向于极其接近的程度。最终，在第500 次迭代后结束训练并保存最优降噪模型。

为说明CDAE 的降噪效果及重构中是否会对扰动造成固有特征丢失。选取C8 和C7 为例进行时频域分析，运用快速傅里叶变换[29]将C7 从时域转换到频域。CDAE 的降噪效果如图8 所示。

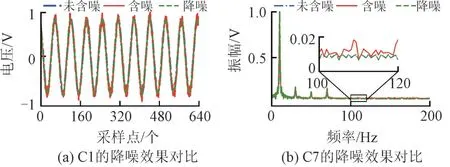
图8 CDAE降噪效果Fig.8 Noise reduction effect of CDAE

由图8 可知，由C1 的时域对比可以看到运用CDAE 降噪后的信号与原始信号非常接近。由C7的频域对比可以看到信号被进行重构后，基本上能够很好地保留信号的固有特征。

将重构信号输入TCN/BLSTM 进行训练。当验证准确率连续3 次迭代不再增加，则第4 次迭代可通过衰减策略将学习率衰减为0.7 倍，最终在第60次迭代结束保存最优分类模型。TCN/BLSTM 的训练过程如图9 所示。

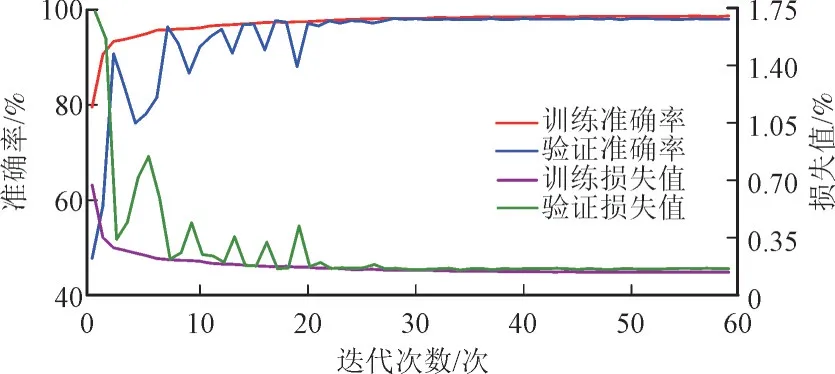
图9 TCN/BLSTM的训练过程Fig.9 Training process of TCN/BLSTM

由图9 可知，随着迭代次数的增加，准确率不断上升且趋于重合，并最终稳定在较高水平；损失值不断下降且趋于重合，并最终稳定在较低水平。训练结束后，验证准确率为99.26%。

对验证集中最高准确率的模型参数进行保存，将信噪比为（20+30+40）dB 的测试集导入最优分类模型中进行测试。评估4 000 个样本共耗时4.24 s，平均耗时为1.06 ms，符合对PQDs 分类的实时性要求[30]。测试集的准确率如表2 所示。

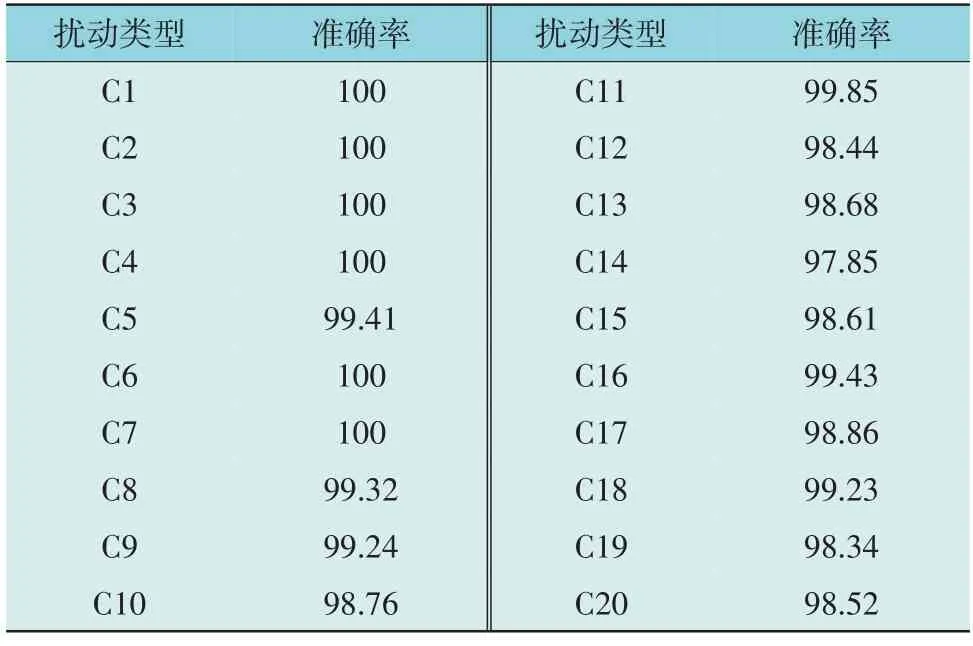
表2 测试集的准确率Table 2 Accuracy of testing set %

由表2 可知，测试集的平均准确率为99.23%，与验证集准确率几乎接近，由此验证了模型的准确性。

3.3 模型对比

为验证所提方法在PQDs 分类问题上的优越性，对分类模型的不同组合和信号进行降噪后再分类进行对比。对比模型的训练参数与本文模型参数保持一致。

3.3.1 不同模型组合

将并行的TCN/BLSTM 模型与单一的BLSTM、单一的TCN 及串行的TCN-BLSTM 模型进行对比，验证集曲线对比如图10 所示。

由图10 可知，随着迭代次数的增加，4 种模型的验证集准确率均不断上升并最终趋于稳定。其中，BLSTM 和TCN 振荡明显，TCN-BLSTM 前期收敛过度、后期缓慢。相比之下，TCN/BLSTM 有着更好的收敛趋势，且验证集准确率更高。

3.3.2 降噪前后

为验证所提方法的噪声鲁棒性，将重构信号输入BLSTM，TCN 和TCN-BLSTM 模型进行训练。训练时同样以验证集精度保存最优为依据对模型进行分类。同时，利用最优降噪模型对信噪比为20 dB，30 dB，40 dB 的测试集进行降噪，并导入BLSTM，TCN，TCN-BLSTM 和TCN/BLSTM 的最优分类模型进行测试。本文所提模型与其他7 种模型的平均准确率对比结果如表3 所示。

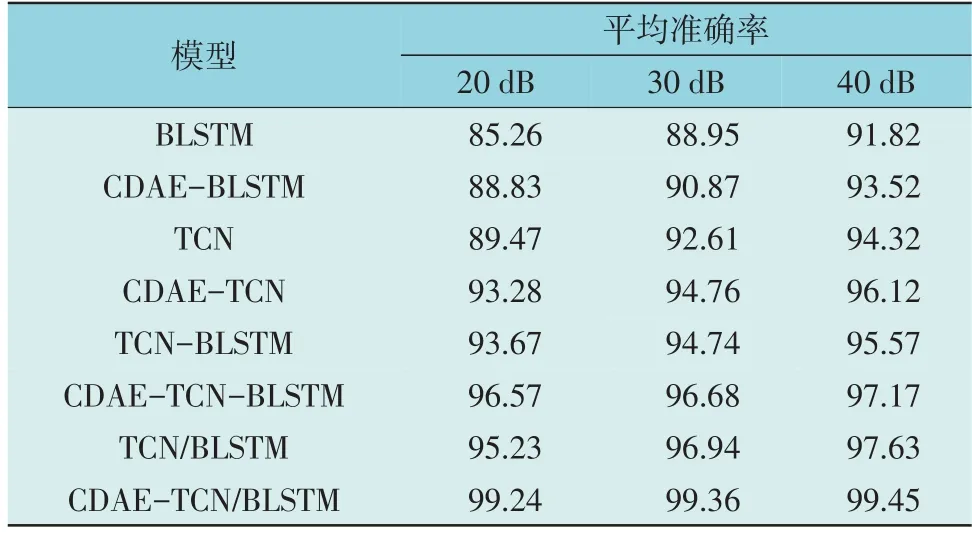
表3 平均准确率对比结果Table 3 Comparison of average accuracy among eight models %

由表3 可知，经CDAE 对信号进行降噪后的分类对比，平均准确率明显有所提高。结合3.3.1 小节的分析，说明本文所提模型的分类精度更高、噪声鲁棒性更强，收敛趋势更快、泛化能力更好，从而验证了所提方法为PQDs 分类的最佳选择。

3.4 与现有研究的比较

3.4.1 性能参数

为体现本文并行部分TCN/BLSTM 模型的先进性，将其与串行的卷积-长短期记忆（Convolutional Long Short-term Memory，C-LSTM）模型、全卷积-长短期记忆（Fully Convolutional Long Short-term Memory，FC-LSTM）模型和TCN-BLSTM 模型进行性能参数的对比。C-LSTM 和FC-LSTM 的基本架构来源于文献[18-19]，性能参数对比如表4 所示。

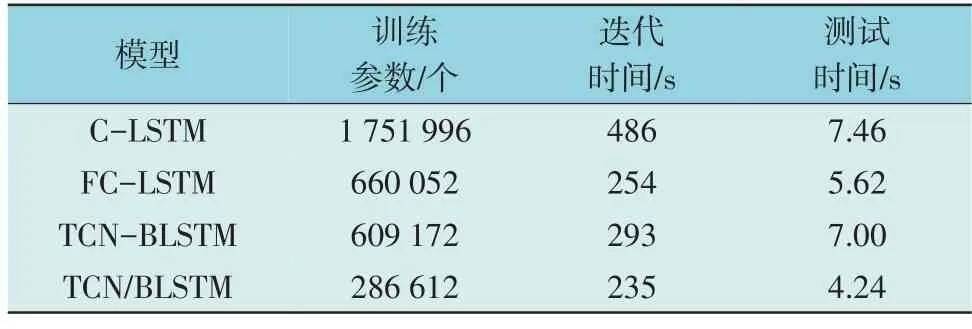
表4 性能参数对比Table 4 Comparison of performance parameter

由表4 可知，TCN/BLSTM 的训练参数更少，说明其复杂度更低[31]。对应的2 种时间参数反应出TCN/BLSTM 的计算速度更快[32]。

3.4.2 分类效果

将所提模型与现有的7 种主流模型进行比较。主流模型为基于离散小波变换（Discrete Wavelet Transform，DWT）和概率神经网络（Probabilistic Neural Network，PNN）的DWT-PNN模型[5]、基于变分模态分解（Variational Mode Decomposition，VMD）和决策树（Decision Tree，DT）的VMD-DT 模型[8]、基于二维卷积神经网络（Two-Dimensional Convolutional Neural Network，2D-CNN）模型[11]、基于稀疏自动编码器（Sparse Automatic Encoder，SAE）模型[15]、多层特征融合注意力（Multilayer Feature Fusion Attention Network，MLFFAN）模型[16]、C-LSTM 模 型[18]或FC-LSTM 模 型[19]。本 文CDAE-TCN/BLSTM 模型与7 种主流模型的平均准确率对比结果如表5 所示。

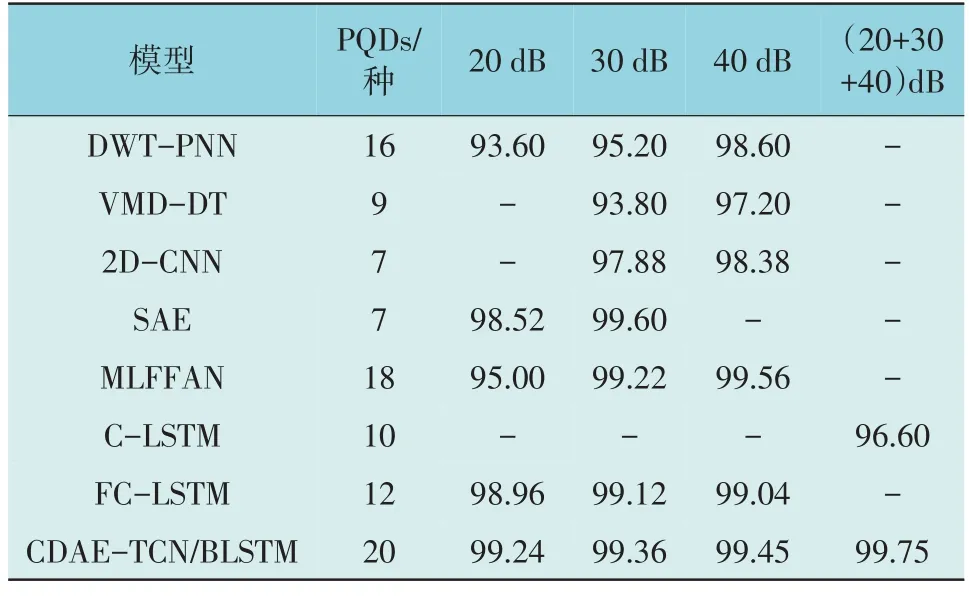
表5 8种模型的平均准确率对比Table 5 Comparison of average accuracy among eight models %

由表5 可知，深度学习模型在不同信噪比下的平均准确率均高于传统方法，这主要得益于深度学习可以准确和自动地提取不同扰动的最关键特征。不同信噪比下，本文模型准确率的波动较小，噪声鲁棒性更好。

4 结论

为有效提升PQDs 信号的分类准确率，本文提出基于CDAE 和TCN/BLSTM 模型的电能质量扰动分类方法，经过对比分析和研究，得出以下结论：

1）所提的CDAE 模型，能够充分学习原始和含噪信号间的特征联系，并保留被噪声掩盖的固有特征。重构信号能准确地表达不同关键信息。

2）所提的并行TCN/BLSTM 模型，能够显著减少深层网络造成的参数量。经BN 优化可有效提升模型的训练速度和解决过拟合等问题。

3）在信噪比为20～40 dB 环境中，基于CDAE 和TCN/BLSTM 相结合的分类方法，对20 类PQDs 的平均分类准确率可达99.23%。在信噪比为20 dB，30 dB，40 dB 环境中，平均准确率分别为99.24%，99.36%，99.45%，较小的准确率波动进一步体现了模型的抗噪能力。

4）与一般分类法相比，本文方法具备模型结构紧凑、噪声鲁棒性强和分类精度高等优点。未来的研究将集中在增加更多复杂扰动和对模型进行优化上。