基于业数融合的电力系统数据质量监测方法

张宝月，梁 潇，陈 曦，田 双，张可心，李 程，马恒瑞

（1.国网陕西省电力有限公司信息通信公司，陕西西安 710000；2.国网陕西省电力有限公司，陕西西安 710000；3.青海大学能源与电气工程学院，青海西宁 810016）

0 引言

随着电力系统数字化建设的不断深入，以数据驱动业务创新的发展模式对数据质量提升需求呈现爆发式增长态势，亟需通过数字化手段对电力系统异常数据进行规范性监测，加强数据质量管理、拓展数据质量监测范围，进一步提升数据管理应用水平[1-2]。随着分布式电源的不断渗透，以新能源为主体的电力系统在运行过程中将面临更大的不确定性[3-5]。一方面，由于不可预测的环境噪声以及虚假数据干扰的客观存在，系统状态的计算值与真值的偏差具有随机性[5-7]；另一方面，测量设备和测量过程也受到随机因素的干扰[8-9]。因此，准确掌握电力系统的运行状态，研究一种电力系统数据监测方法，对于提升电力系统运检业务数字化水平具有重要意义。

随着先进计量基础设施的普及，电力系统传感器网络和数据的网络安全已成为电力系统运行和控制的关键[10-12]。文献[13]通过将估计测量值与实际测量值之间的加权差平方和最小化处理来降低估计误差，提升状态估计的精确性。文献[14]提出了一个用于不确定性分析的约束非线性优化问题，以获得状态变量的最紧可能上界和下界。文献[15]提出了一种改进的归一化拉格朗日乘数测试来识别和检测参数误差，可以保护评估过程免受不确定性的影响。然而估计结果仍然容易受到某些测量的影响。随着现代电力系统向智能电网的发展，分布式可再生能源和独立系统运营商越来越多，系统在现实中变得更加动态和时变，因此，基于稳态电力系统假设的传统静态状态估计不再有效[16]。文献[17]提出了一种基于扩展卡尔曼滤波方法的横向二级动态状态估计算法，然而，卡尔曼滤波算法在计算雅可比矩阵时会产生截断误差并降低估计精度。

由于系统传输信息的误差以及不准确的建模会导致电力系统状态估计模型的不确定性，从而影响估计结果的准确性。在存在异常值或不确定性的情况下，鲁棒估计器可提供可接受结果[18-19]。然而，提高状态估计的鲁棒性往往会降低估计精度。为此，考虑到不同程度的非高斯分布测量噪声和不良数据，文献[20]提出了一种基于采样的优化参数广义M-估计的电力系统状态估计方法。文献[21]提出了一种新的多级混合状态估计器，能够实时校正整个电力系统的状态估计结果。文献[22]采用旋转量测变换，利用相量测量单元（Phasor Measurement Unit，PMU）的电压相角量测信息将电流量测转化成为旋转量测，实现了状态量在极坐标下的解耦，改善了静态状态估计的精确性。然而，除了测量误差和异常值的不确定性外，网络建模优劣也会影响估计结果的准确性[23-25]。

电力系统所面临的不确定性不止局限于测量误差和异常值，而且还归因于网络的不准确建模以及虚假数据的注入[26-29]。为此，本文提出一种基于业数融合的电力系统数据质量监测方法，用以提升业数融合背景下电力系统状态监测的精度和速度，更适应新型电力系统发展的需要。

1 状态估计模型构建

量测模型采用混合量测，在某些节点配置PMU，量测量为节点电压的幅值和相角。其余节点覆盖监视控制与数据采集（Supervisory Control and Data Acquisition，SCADA）系统，量测量为注入的有功、无功功率和电压幅值[30-31]。包含m个测量和n个未知参数的测量模型可表示为：

式中：z为测量向量；x为状态变量；h(x)为测量值和系统状态之间关系的非线性函数向量；e为测量误差向量。

在实际系统运行过程中总存在测量误差{e1,e2,…em}，即m阶测量向量z与m×n阶状态变量向量h(x)并不总是匹配。因此，测量误差向量e的对角协方差矩阵可以表示为：

式中：σi为第i个测量值误差的标准偏差。

除了在基于物理的模型中使用的空间信息外，本文基于业数融合的机器学习算法来利用电力系统的时间和空间信息，保留空间上相邻的相关性。在机器学习层通过已验证的数据来学习正常运行时的电网状态，进而检测系统的所有异常数据，并将其与系统的其余部分隔离。根据分布的平均值计算输入数据的马氏距离，目标函数可以表示为：

其中，

式中：W为m×m的加权矩阵。

对x求偏导，即：

式中：g(x)为目标函数J(x)对x求的偏导；G(x)为g(x)对x求的偏导；H(x)为h(x)对x求的偏导。

系统状态估计结果可通过递推公式进行迭代计算，即：

式中：xk为第k次迭代的状态估计；Δxk为第k次迭代的状态估计变化量；ζ为极小的常数，表示迭代停止条件，其值越小则结果越准确。

2 异常数据判定和不确定性处理

通过异常数据检测器对输入样本进行训练，基于式（3）确定其平方马氏距离，并将其与阈值τ进行比较，即：

式中：δCD(z)为测量向量的平方马氏距离值。

当结果低于阈值时，新数据为正常数据，当结果高于阈值时，则将新数据标记为异常。为了选择马氏距离的阈值τ，将τ作为训练数据集中所有正态样本马氏距离值的标准差σthr和平均值μthr的函数进行变化，如（11）所示：

式中：η为调节系数。

在空间层面，当系统受到攻击时，距离较近的节点之间相关性更高，而距离更远的节点则相关性较小。因此，当训练数据有限时，无需学习所有节点的协方差总体测量，使用测量较少的局部区域即可，这些区域具有更小的维度并提供更准确的正态分布，同时在计算上更快速并能够提供更灵敏的异常检测，从而降低空间上相邻节点的测量值。

在本文所提状态估计算法中，测试集中的每个样本具有M个马氏距离，将每个区域一个距离作为其决策得分，然后与状态估计器的决策得分ΨSE相结合，得到每个样本的总体决策得分。ΨSE的计算公式可以表示为：

式中：CMEi为第i个测量值的测量误差；σi为第i个测量值误差的标准偏差；d为测量个数。

由于电力系统在实际运行过程中面临大量的不确定性因素，如互联数据质量、拓扑关系数据质量，因此基于加权最小二乘法（Weighted Least Squares，WLS）法的标称数据{z,H}在受到干扰后将影响到估计结果的准确性。为解决该问题，可通过鲁棒估计器将传统模型进行最小-最大优化，考虑不确定性的测量模型可以表示为：

式中：δz为m×1的干扰向量；δH为m×N干扰矩阵。

在该模型中，假设测量值和网络参数均具有不确定性，即：

式中：S，EH，Ez为已知不确定度参数；Δ 为有界的不确定性因子。

考虑不确定性的状态估计模型的目标函数为：

为便于模型求解，首先将式（15）进行简化：

式中：Sy为m×q的已知矩阵；q为不确定性参数Δ的维数；y为q×1 未知扰动向量；ϕ(x)=‖EHx-Ez‖为上界。

令R=W-1，于是，式（15）可以改写为：

式中：x为状态变量；Hx为函数向量。

式中：‖Hx(λ)-z‖R(λ)为向量Hx-z的加权范数；S为已知矩阵；EH为状态误差向量；Ez为测量误差向量；I为随机向量。

式中：μ为常数。

3 仿真分析

为了验证所提出的状态估计方法的有效性，在修改后IEEE 30 节点系统进行仿真计算分析，其拓扑结构如图1 所示，其中G 为发电机节点。

图1 修改后IEEE 30节点拓扑结构Fig.1 Revised IEEE 30-node topology structure

为了计算测量值，首先运行潮流以生成真实数据，然后将与每种测量类型对应的测量误差方差σ2添加到数据中，以产生含有噪声的测量值。由于整个系统需要足够的测量冗余进行观察分析，因此，将调节系数η设为1.7。对于测量的标准偏差，传统测量误差为1%，相量测量误差为0.1%。对于系统的不确定度参数Ez和Eh，将z和H均设为5%。相关系数S设为1，Δ 为0.5，μ为0.5。为验证本文方法的有效性及优越性，设置3 种场景进行对比分析：场景1 为本文所提出方法；场景2 为不考虑不确定性的混合状态估计方法；场景3 为基于最小绝对值（Least Absolute Value，LAV）的状态估计方法。

为比较不同方法下从潮流运行中获得的估计状态变量和真实值之间的误差，3 种场景下IEEE 30节点电压幅值与相角的估计误差如图2 与图3所示。

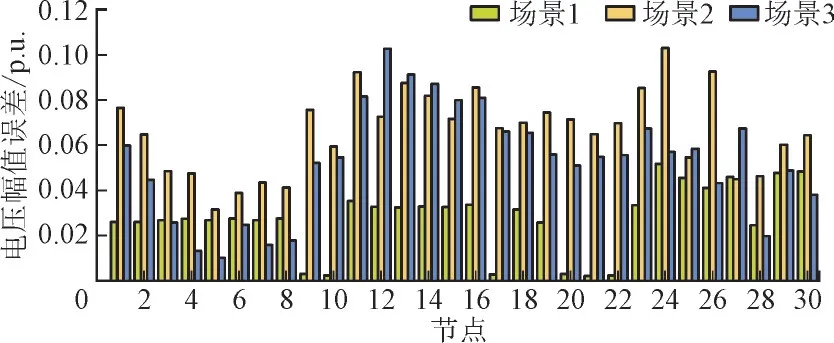
图2 3种场景下的电压幅值误差对比Fig.2 Comparison of voltage amplitude errors in three scenarios

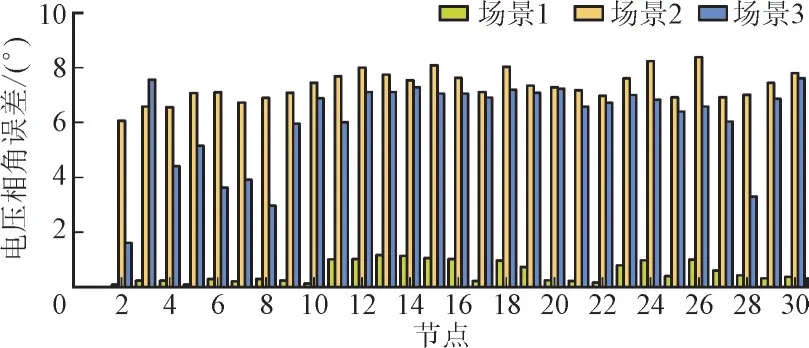
图3 3种场景下的电压相角误差对比Fig.3 Comparison of voltage phase angle errors in three scenarios

由图2、图3 可以看出，相对于另外2 种方法，本文所提方法的估计误差更小，可以有效限制系统的不确定性，从而提供更为准确的估计结果。

3 种场景下的计算时间如表1 所示。由表1 可以看出，相对于方法2 和方法3，本文所提方法计算效率更高，分别提升了5.7%和19.1%。

表1 IEEE 30测试系统不同估计器计算时间的比较Table 1 Comparison of calculation times of different estimators in IEEE 30-node test system s

为了验证本文算法的鲁棒性，通过将不确定度的范围增加到20%进行不确定度评估。不确定度分别为5%，10%和20%的状态估计结果如图4、图5 所示。

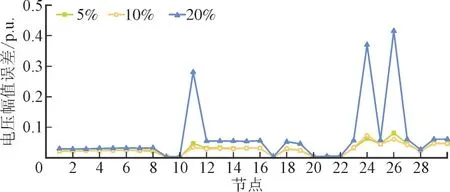
图4 不同不确定度下的电压幅值误差对比Fig.4 Comparison of voltage amplitude errors under different uncertainties

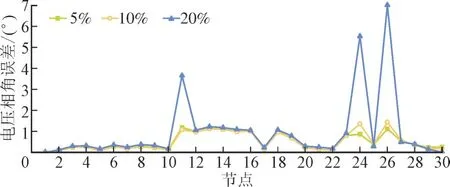
图5 不同不确定度下的电压相角误差对比Fig.5 Comparison of voltage phase angle errors under different uncertainties

为了评估参数μ对基于相量测量单元的电力系统鲁棒混合状态估计方法性能的影响，进行了灵敏度分析，不同μ值下IEEE 30 节点系统的电压幅值和相角误差对比结果如图6 与图7 所示。由图6、图7 可以看出，随着μ值的增大，系统的估计误差呈现增长的趋势。当μ处于0.5～10 的区间时，误差基本一致，但当μ值过大时则出现显著的误差。因此，μ值较小时可获得较为精确的估计结果。

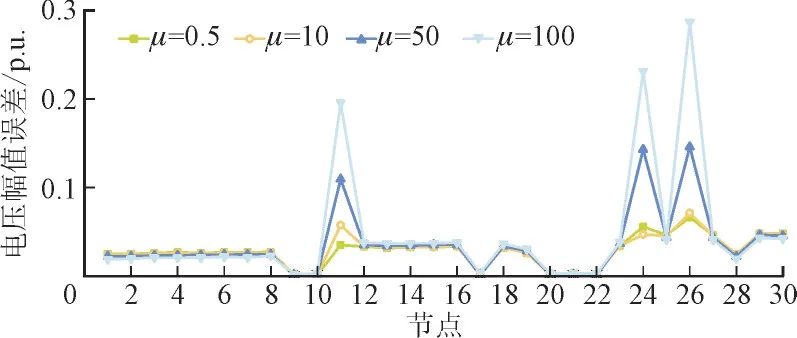
图6 不同μ 值下的电压幅值误差对比Fig.6 Comparison of voltage amplitude errors under different values of μ

图7 不同μ 值下的电压相角误差对比Fig.7 Comparison of voltage phase angle errors under different values of μ

3 种场景下测量结果的标准差如表2 所示。由表2 可以看出，相对于场景2 和场景3，本文所提方法的误差偏差更小，估计更为精确。

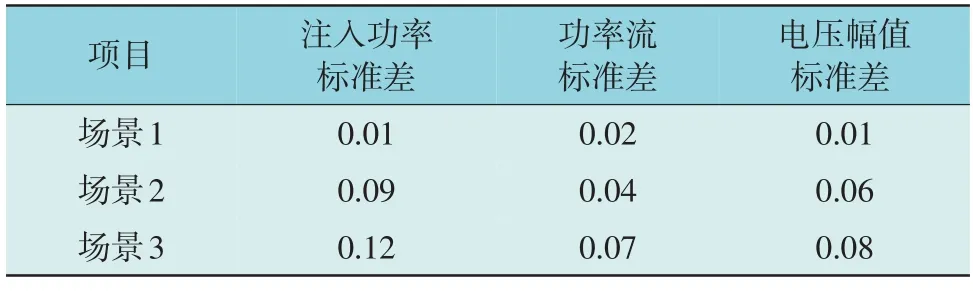
表2 3种不同情况下测量的标准偏差Table 2 Standard deviation of measurements under three different scenarios

为验证本文所提方法的适用性，分别在IEEE 57 节点系统和IEEE 118 节点系统进行仿真计算。不同系统下的计算时间以及均方误差（Mean Square Error，MSE）如表4 所示。MSE 的计算公式如式（25）所示，

由表3 可以看出，随着系统规模的增加，计算时间也随之增加，但并不明显，可控制在1 s 之内。与IEEE 30 节点系统相比，IEEE 118 节点系统和IEEE 57 节点系统的电压幅值均方误差以及电压相角均方误差变化也并不明显，呈现较为稳定的估计结果。可见，本文所提方法具有较高的适用性，可对规模较大的电力系统进行精确的数据质量监测。

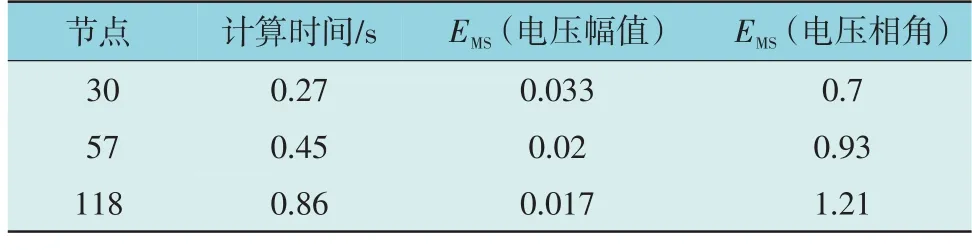
表3 不同测试系统的计算时间和均方误差比较Table 3 Comparison of calculation time and mean square error for different test systems

4 结论

本文提出一种基于业数融合的电力系统数据质量监测方法。仿真结果表明通过业数融合，本文方法在计算上更快速并能够提供更灵敏的异常检测，从而降低空间上相邻节点的测量值。同时，通过结合非同步传统和同步相量测量，可以有效提高状态估计的精度，通过评估不确定度参数下状态估计的结果，验证了所提方法的鲁棒性。从而为电力系统各项业务高效运转打好数据基础，激发数据在内部提质增效，全面提升管理层综合业务分析能力，有效支撑管理层快速、准确决策。