基于图多任务学习的潮流分析模型

李駪皓，梁志坚，刘敏，杨武，潘智冲，王骁睿

（1.广西大学电气工程学院，南宁 530004；2.暨南大学能源电力研究中心，广东 珠海 519070；3.北京师范大学人工智能学院，北京 100875）

0 引言

潮流分析在电网规划和设计、电网运行状态分析、电网故障分析中有着广泛的应用。然而随着我国电网的发展，不同区域间电网互联更加紧密，电网设备负载加重，传统潮流计算方法如牛顿-拉夫逊（Newton-Raphson，N-R）法易出现病态潮流［1］，造成求解速度慢、潮流计算不收敛等问题［2］，在实时在线潮流分析、概率潮流计算、电网安全性校核等需大批量潮流计算的场景中尤为突出。

作为数据驱动类方法，基于深度学习的潮流分析方法可以直接拟合现实电力系统潮流初值到潮流分布之间的映射关系，无需迭代计算雅可比矩阵，因此时间复杂度仅随节点规模增长呈线性关系，且不会出现雅可比矩阵条件数过大导致病态潮流问题［3］。国内外研究者们注意到了这一优势并展开了相关研究。早在20世纪80年代，文献［4］就提出利用多层感知机（multilayer perceptron，MLP）对潮流分布进行求解；文献［5］在训练中模拟了一些简单的偶发情况，使得模型能够计算简单偶然情况下的电网潮流分布；文献［6］则以支路开断前后各支路的有功功率之差表征网络拓扑结构的变化，使得模型可以计算电网支路故障后的潮流分布。

上述基于欧式数据的神经网络虽在潮流分析问题中取得了一定的成效，但却忽略了电力系统潮流数据作为图结构数据的实质，定义在欧式域中的一些关键计算，如卷积计算并不适用于处理不规则的图结构数据［7］。因此，可以直接接受任意节点规模、任意拓扑结构的图结构数据作为输入，实现端到端学习的图神经网络（graph neural network，GNN）［8］更契合潮流分析问题的需求。文献［9］基于图卷积神经网络（graph convolution network，GCN）［10］提出了纯数据驱动的潮流分布计算方法；文献［11］则更进一步将GCN 潮流计算模型嵌入概率潮流分布计算中；文献［12］则在GCN 潮流计算模型训练过程中令其最大程度满足实际物理规律约束；文献［13］考虑潮流计算存在不同节点类型，提出通过类型图网络（typed graph networks，TGNs）［14］求解潮流分布。

然而现有基于深度学习的潮流计算方法局限于潮流分布计算，仅利用神经网络拟合潮流初值信息到潮流分布之间的关系，未考虑潮流不收敛情况。从神经网络建模的角度来看，潮流分布计算则是以潮流初值为输入变量，以潮流分布作为输出的回归问题，而潮流判敛是以潮流初值为输入变量，以潮流是否收敛为输出变量的二分类问题，二者在模型结构上存在本质性的区别［15］。因此基于回归模型的潮流分布求解模型不具有潮流判敛功能，对输入的潮流不收敛的案例仍会给出虚假的系统潮流分布，只能用于求解收敛的潮流分布。此缺陷极大程度地限制了深度学习潮流计算方法的实际应用，目前有关基于数据驱动的潮流判敛研究较少。文献［16］在DNN 输入特征中加入无功功率调节能力指数集及功率因数水平指数集进行潮流判敛，然其受限于DNN 框架无法应用于网络拓扑变化的电网中且不考虑潮流分布计算，尚需更深入地研究。

针对此问题，本文提出了一种全新的适用于潮流分析问题的图多任务学习模型，在保持基于深度学习的潮流计算方法优势的同时，解决其不考虑潮流不收敛问题。

本文主要工作如下。

1）在模型结构方面，建立适用于潮流分析任务的图多任务学习模型，模型同时具备潮流判敛及潮流分布计算功能。

2）针对潮流计算中不同类型节点具有不同潮流初值问题，通过异构特征提取层对潮流计算中PQ、PV与Vθ节点的输入特征进行差异化处理。

3）在图神经网络方面，针对经典图卷积与图池化方法不考虑边信息的缺陷，结合电力系统物理特性改进图注意力机制，提出双视角图注意力网络（double-view graph attention network，DGAT），并将其应用于图池化计算中，提出图自注意力聚合池化方法（graph self-attention aggregation pooling，GSAPool）。

1 基于图神经网络的潮流分析

1.1 潮流分析问题图结构数据建模

潮流计算中所需节点信息包含节点类型T、电压初值U、相角初值θ，负载的有功功率PL和无功功率QL，发电机的有功出力PG、无功出力QG，由于潮流计算中发电机节点无功越限会导致节点类型转换［17］，本文在节点信息中加入发电机无功功率上下限Qmax、Qmin，使所提模型可以隐式地考虑节点类型转换对潮流收敛性的影响。边信息则为线路导纳yij。电网G={V，E}为节点集合V与边集合E。vi∈V表示图中第i个节点，其特征（若节点为非发电机节点则、Qmax及Qmin均为0），所有节点特征可用节点特征矩阵HN×9=表示，N为节点数量。由于节点特征向量涉及电压、相角、功率3 个不同量纲间的值，为了消除数据特征之间的量纲影响，对节点特征向量进行标准化处理。

不同于一般的图结构数据，在潮流分析中拓扑关系及边属性都可通过节点导纳矩阵YN×N来表示。节点导纳矩阵非常直观地反映了电力系统的拓扑连接方式及线路导纳，因此本文所提图分类器直接采用节点导纳矩阵作为边特征。

1.2 基于DGAT-GSAPool的图多任务学习模型

本文所提图多任务学习模型的整体结构如图1所示，在通过同构化层消除图中异构性后，通过六层DGAT 图卷积层对图中节点特征进行提取。为提取全图特征，在前两层DGAT 图卷积层后进行GSAPool 全局图池化计算。同时，采用残差结构避免训练过程中的梯度消失问题。最后，将两层图池化层提取出的全局图特征拼接后输入图分类器，将最后一层图卷积层提取出的节点特征作为系统潮流分布，获得潮流分析结果，即潮流是否收敛与潮流分布情况。模型各层详细参数如表1 所示，模型中激活函数采用RReLu 函数，RReLu 函数为改进的LeakyReLu 函数，在保留其避免神经元死亡优势的同时，可以更好地避免过拟合。其计算公式如式（1）所示。

图1 DGAT-GPPool图分类器结构Fig.1 Structure of DGAT-GPPool graph classifier

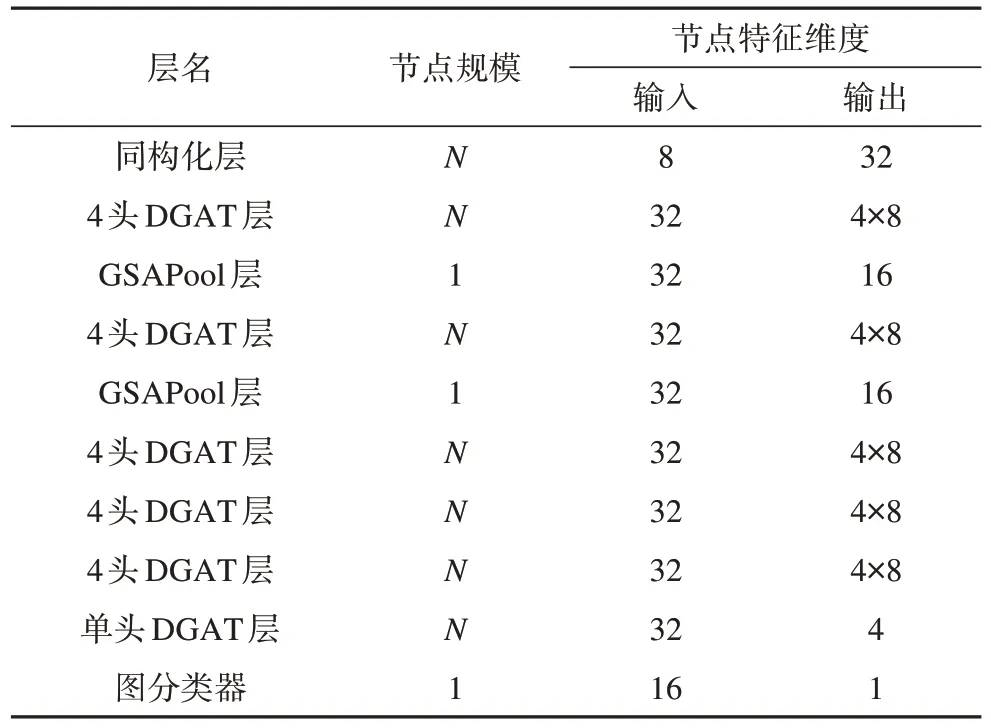
表1 DGAT-GPPool图分类器结构参数Tab.1 DGAT-GPPool graph classifier structure parameters

式中α～为随机常数。

1.3 同构化层

由于电力系统实际条件的限制，从不同节点获取的潮流初值存在差异，潮流计算中将节点分为PQ、PV及Vθ节点三类，因此从潮流计算的角度来看，电力系统天然为一张异构图。异构图中的节点通常具有不同的特征［18］，直接将基于同构图的图神经网络用于异构图通常不具有说服力［19］，因此需要一些额外的工作来消除图的异构性。本文所提模型对不同类型节点的特征采用不同的可学习线性变换进行特征提取，经特征提取后异构图可视作同构图，提取方式如式（2）所示：

1.4 双视角图注意力网络层

针对经典图卷积方法不考虑边属性的缺陷，本文提出考虑线路导纳的双视角图注意力机制。结合电力系统中两节点间线路导纳越大相互联系越紧密这一物理特性，双视角注意力机制在通过经典图注意力机制［20］计算出节点注意力系数的同时，根据线路导纳计算出边注意力系数，最后通过可学习权重参数将两视角下的注意力系数加权平均得到综合注意力系数，计算公式如式（3）所示。

图卷积运算通过消息传递聚合机制定义了每个节点上的局部图卷积［7］，让每个节点聚合其邻居节点及自身的特征向量用以计算自身新的特征向量，使得神经网络能感受图的拓扑结构。如图2 所示为多层图卷积运算中消息传递聚合机制示意图，可见节点特征在图上的传递可以类比于能量在电网上的流动，因此基于消息传递聚合机制的图卷积方法更适用于求解潮流分析问题，可以进一步地提高模型的可解释性［21］。

图2 消息传递聚合机制示意图Fig.2 Schematic of the messaging aggregation mechanism

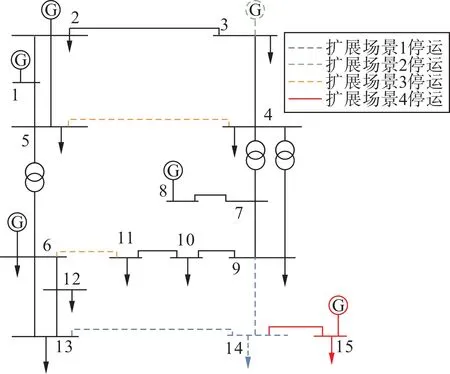
图3 源场景及扩展场景电气接线图Fig.3 Electrical wiring diagram in the source and extension scenes

计算出综合注意力分数之后，DGAT 通过如式（4）所示消息传递聚合机制完成节点特征的更新。

1.5 图自注意力池化层

基于GNN 的图分类方法主要运用图卷积运算对图域数据的进行特征提取［14］，通过图池化运算总结出代表全图信息的图级特征，最后将图级特征输入分类器完成图级的分类［22］。

作为基于GNN 的图分类方法中必不可少的一环，图池化对潮流判敛问题的图分类求解至关重要。然而主流图池化方法同样不考虑边属性对图级特征的影响。针对此问题，结合上一节中所提DGAT 方法，本文提出一种考虑边特征的全局图池化方法。

图自注意力池化方法首先计算每个节点的注意力权重。通过DGAT 图卷积方法，综合考虑图中节点特征、边特征与网络拓扑，为图中所有节点赋予一个自注意力系数，自注意力系数越高的节点在图中的重要性越大。所得自注意力系数在归一化后作为自注意力权重，其计算公式如式（5）所示。

式中：H为节点特征矩阵；Y为节点导纳矩阵；为各节点权重组成向量。DGAT 为1.4 节所述双视角图注意力网络，其输出特征纬度为1；softmax(·)为归一化函数，计算公式如式（6）所示：

式中n为需归一化的元素总数。得到各节点自注意力权重后，通过加权平均聚合图内所有节点特征以获得图级特征向量，最后通过可学习线性变换缩减其参数量。计算公式如式（7）所示：

1.6 图分类层

在图多任务学习模型中，图分类层对图池化层提取出的全局图特征进行最后的处理，使其重新具备实际的物理意义以满足图分类任务要求。如图1所示，图多任务学习模型在堆叠的DGAT 图卷积层中添加数层GSAPool层以提取不同层次下的图级特征向量，因此本文先通过注意力结构将多层图级特征向量进行特征聚合，计算公式如式（8）所示：

式中：r为模型图分类任务最终输出分类结果，当r＜0.5 时表示输入样本潮流不收敛，否则表示潮流收敛；sigmoid(·)为激活函数，将MLP 输出值映射到[0，1]之间，其计算公式如式（10）所示：

2 算例分析

2.1 数据生成

本文训练集及测试集选取IEEE14 节点系统作为源场景，在源场景的基础上考虑节点故障、线路检修、发电机检修及设备投运设计4 种扩展场景，源场景及扩展场景电气接线图如图4 所示。在源场景及扩展场景基础上通过修改各场景中节点电压、相角、有功出力、无功出力、有功负荷、无功负荷、线路电阻及电抗值得到样本，各参数均以初始参数为基准值在70%～130%间按均匀分布随机波动。

图4 图分类任务损失下降过程Fig.4 Graph classify task loss descent process

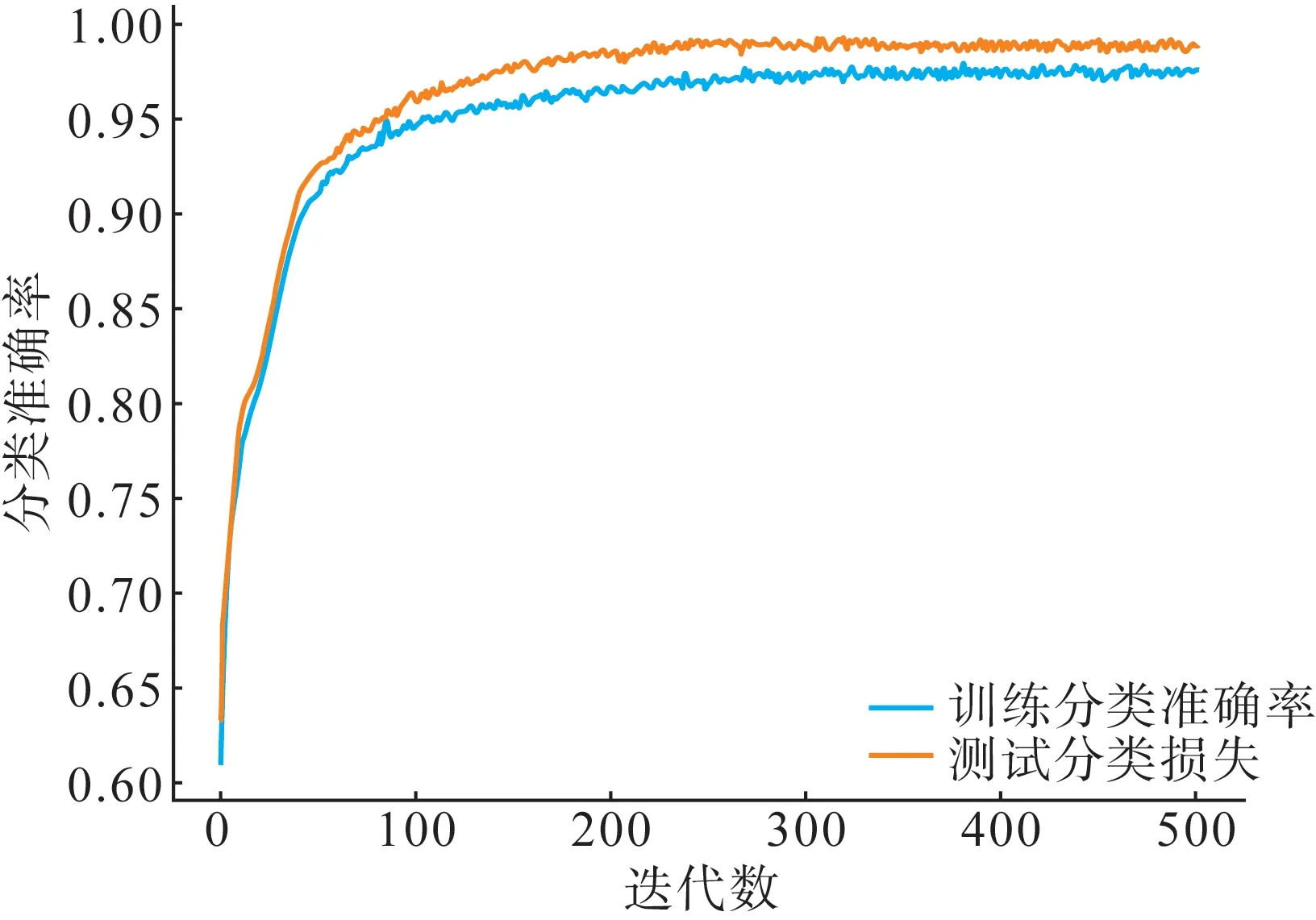
图5 图分类任务准确率上升过程Fig.5 Graph classify task accuracy rise process

样本生成后利用基于Python环境的潮流工具包pypower 对样本进行基于N-R 法的潮流计算，设置误差阈值为ε=10-8，最高迭代次数为50 次，根据计算结果对样本进行标注。最终取8 000 份潮流样本作为训练集，2 000 份潮流样本作为测试集，训练集与测试集中潮流收敛样本占总样本数的50%，满足数据均匀分布要求。本文模型使用python语言编写，基于pytorch框架完成。

2.2 模型性能分析

本文将模型性能分为计算精度与计算速度两个维度，并对其分别进行测试。

在计算精度方面，本文将所提基于DGATGSAPool 的图多任务学习模型投入2.1 节所述数据集进行500次训练与测试。

在图分类任务方面，模型通过二元交叉熵（binary cross entropy，BCE）损失计算方法作为模型在图分类问题上的损失函数，训练过程如图4—5所示。

由图4 可以看出，在约300 轮训练后本文所提图多任务学习模型分类任务上的损失不再下降。最后一轮训练后，模型在训练集上损失为0.073 4，准确率达到97.52%，F1 分数达到0.977 4；在测试集上损失为0.064 7，准确率达到98.81%，F1 分数达到0.988 2。

在回归任务方面，模型通过平均百分比误差（mean absolute percentage error，MAPE）损失作为模型的在图回归问题上的损失函数，训练过程如图6所示。

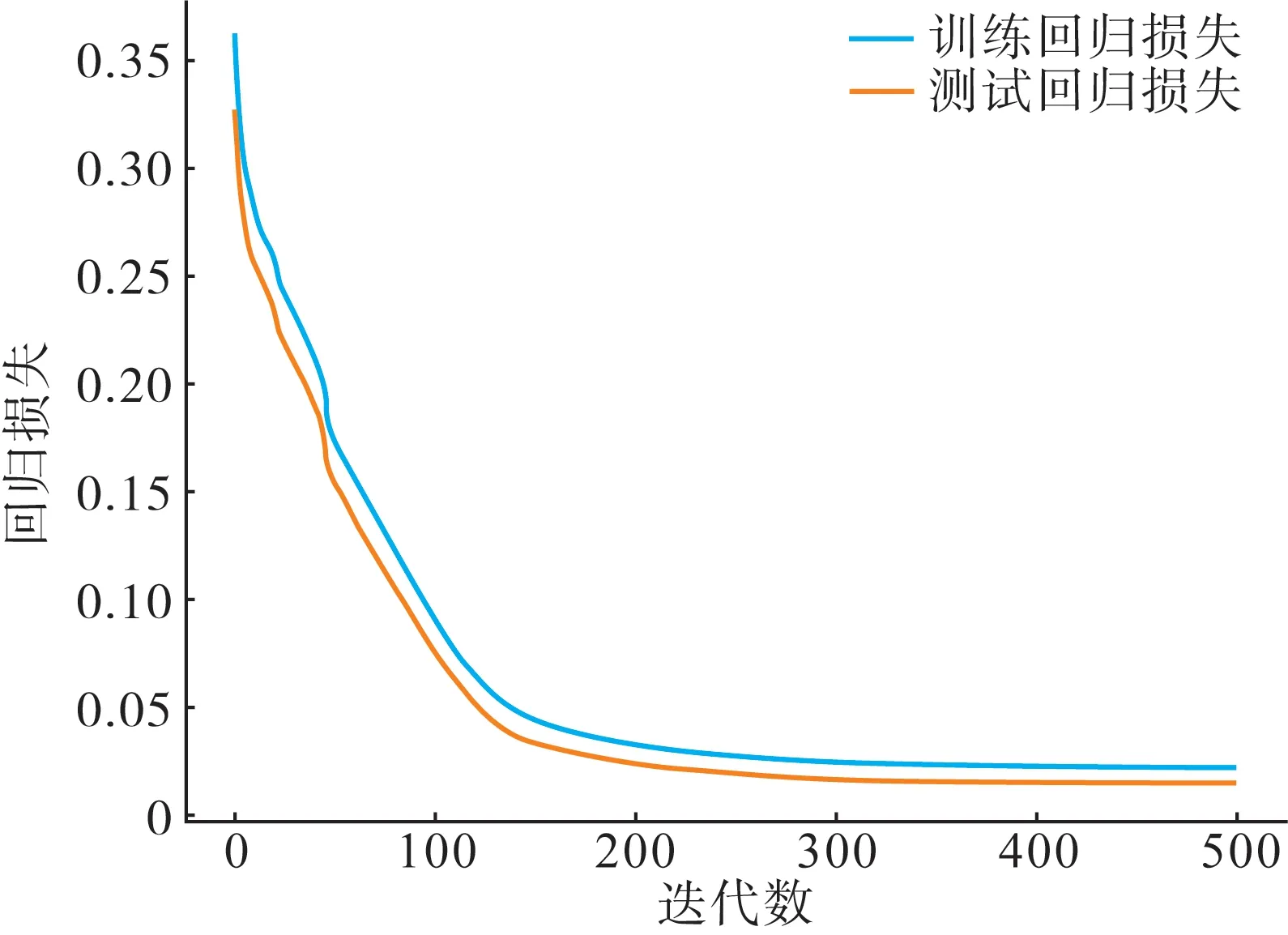
图6 图回归任务损失下降过程Fig.6 Graph regression task loss descent process

由图6 可以看出，同样在约300 轮训练后本文所提图多任务学习模型回归任务上的损失不再下降。最后一轮训练后，模型在训练集上损失为0.021 8，在测试集上损失为0.014 2。由于回归任务损失通过MAPE 方法计算得到，因此模型在训练集上精度97.82%，在测试集上达到98.58%。

在计算速度方面，由于N-R 法通过迭代计算求解，其求解速度取决于输入潮流初值的优劣，难以通过时间复杂度分析的方法对其进行评估，因此本文采用实测的方法进行计算速度的对比。

基于DGAT-GPPool 图分类器的潮流判敛方法与传统计算方法在对不同规模的10 000个系统样本进行潮流判敛的耗时如表2 所示，测试数据集生成方式与2.1 节一致。由于pypower 在计算时无法通过GPU 加速计算，出于公平的目的，测试时DGAT-GPPool图分类器亦未采用GPU加速计算。

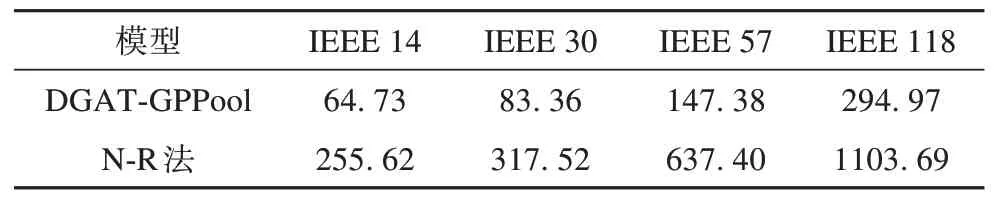
表2 计算速度对比Tab.2 Calculation speed comparisons s

从表2 可见，本文所提图分类器直接拟合了系统稳态信息到系统是否潮流收敛及潮流分布的映射关系，因此可直接根据输入的图结构数据判断此系统是否潮流收敛及求解系统潮流分布，无需迭代求解雅可比矩阵，因此在计算耗时方面约为传统计算方法的四分之一。

2.3 消融实验及对比试验

2.3.1 实验设置

为验证本文所提基于DGAT-GSAPool的图多任务学习的有效性，本文将所提模型与经典图卷积及图池化算法进行对比，对比实验中仅使用对比模型替换所提图多任务学习模型中对应部分，并不改变模型整体结构，模型结构与超参数设置均如1.2节所示。所有模型均基于3.1节中所述训练集进行训练，评估结果也均基于相同测试集上的测试结果计算得到。

2.3.2 图卷积方法对比

在同构化层消融实验中，本文将验证同构化层的有效性将所提模型与未添加同构化层的相同模型进行对比。消融实验中仅删去所提模型中对应部分，但为保证后者正常运行，需将模型中第一层4头DGAT 层的输入特征纬度修改为八维，其余超参数保持不变。由于同构化层同时影响图分类及图池化任务，因此此处对比各组模型的总损失，各模型在测试集上表现如图7所示。

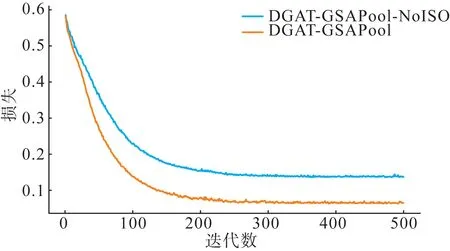
图7 同构化层消融实验总损失下降过程Fig.7 Total loss decrease process in isomorphic layer ablation experiments

从图7 可以看出，由于无同构化层模型不具有区分不同类型节点的能力，将来自不同类型节点的不同维度的特征向量直接输入基于同构图的模型中，导致模型整体效果较差。所提模型通过同构化层消除输入样本的异构性，模型效果提升较大，证明本文所提同构化层的有效性。

2.3.3 图卷积方法对比实验

为分析图卷积方法对图分类器表现的影响，选取GCN［10］-GSAPool 模型、GAT［20］-GSAPool 模型、SAGE［23］-GSAPool 模型及所提DGAT-GSAPool 模型进行对比实验，上述模型中GSAPool中所用图卷积方法亦改为对应图卷积方法。由于图卷积方法同时影响图分类及图池化任务，因此此处对比各组模型的总损失，即分类损失与回归损失之和，各模型在测试集上表现如图8所示。

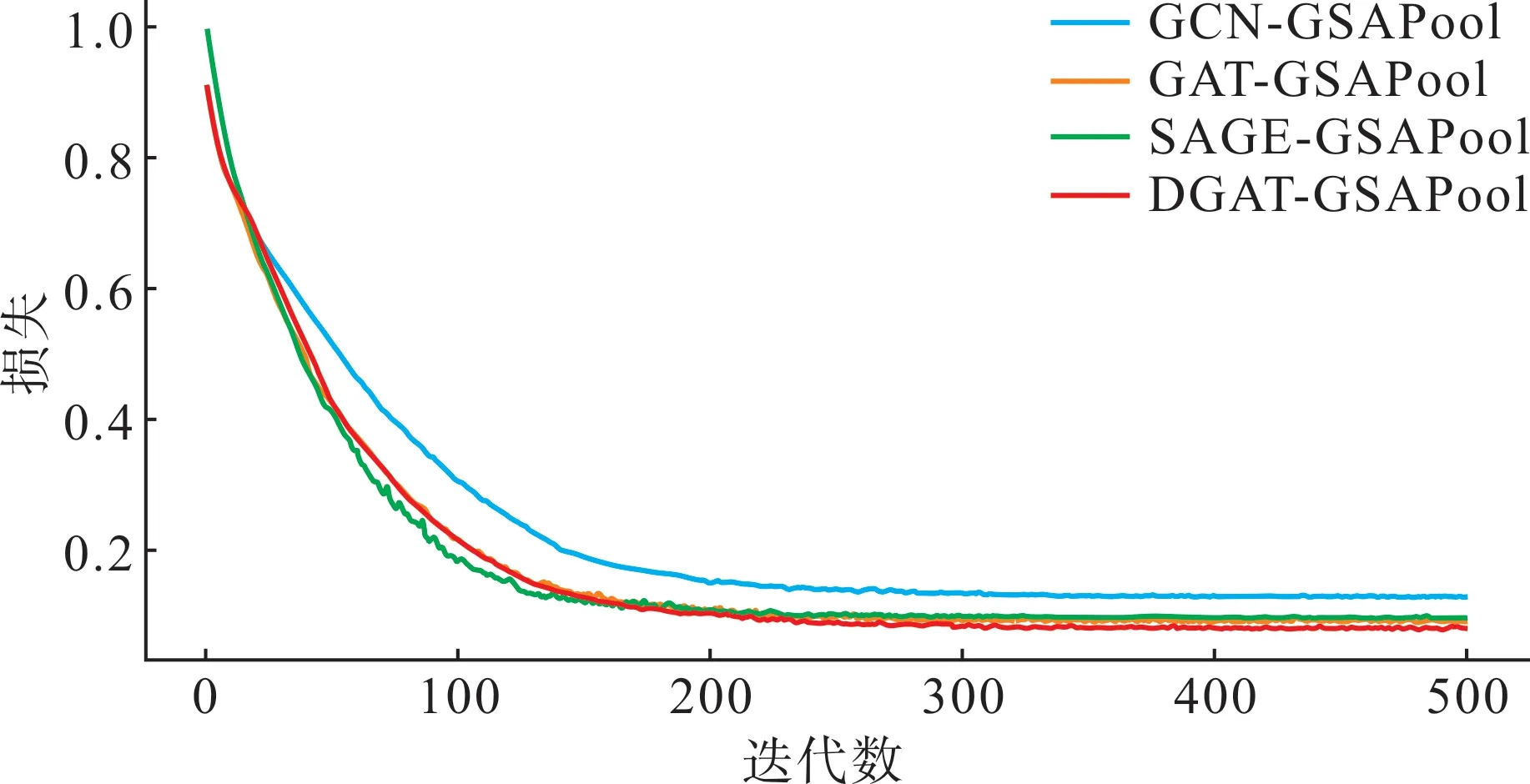
图8 各对比实验组总损失下降过程Fig.8 The decreasing process of total losses in each comparison experimental group

从实验结果中可以看出，在使用相同的图池化方法的情况下，GAT-GSAPool 模型通过自注意力机制放大了来自重要节点的影响，因此在整体效果上优于GCN-GSAPool 模型与SGAE-GSAPool，而在考虑线路导纳信息的DGAT-GSAPool模型在表现略优于前三者，证明本文所提考虑线路导纳的DGAT图卷积方法的有效性。

2.3.4 图池化方法对比实验

为分析图卷积方法对图分类器表现的影响，选取DGAT-MaxPool 模型、DGAT-MeanPool 模型、DGAT-TopkPool［24］模型、DGAT-SAGPool［25］模型及所提DGAT-GSAPool模型进行对比实验。由于图池化方法仅影响图分类任务，对图回归任务不发挥作用，因此此处对比各模型在图分类任务上的损失。各模型在训练集上表现如图9所示。

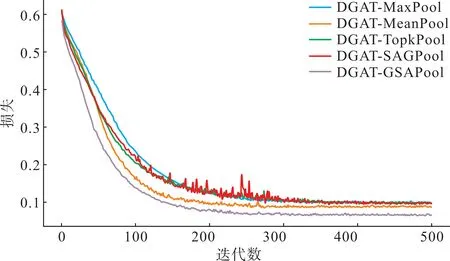
图9 各对比实验组图分类损失下降过程Fig.9 The decreasing process of graph classification losses in each comparison experimental group

从实验结果中可以看出，在使用相同的图卷积方法的情况下，由于进行全局图池化过程中MaxPool、TopkPool 与SAGPool 均仅保留图中最高分节点信息，抛弃其余节点所携带的节点信息，因此这三者的表现相近，整体效果较差。在池化过程中不会产生信息损失的MeanPool 在执行全局图池化时效果由于上述三种模型。而本文所提GSAPool通过子图节点聚合的方法避免了池化过程中的图信息丢弃行为，且在聚合过程中通过DGAT 图卷积方法将边信息纳入池化计算过程，因此整体效果最好，证明本文所提考虑线路导纳的GSAPool图池化方法的有效性。

3 结论

本文针对现有基于深度的潮流计算方法不考虑潮流不收敛问题，提出基于图多任务学习的潮流分析模型，该模型同时具备潮流判敛及潮流分布计算功能，更符合潮流计算问题实际需求。

本文所提DGAT-GSAPool图多任务学习模型在计算过程中结合电网物理特性，在不同网络拓扑结构混合测试集上潮流判敛精度达到98.81%，回归计算精度达到98.58%，计算耗时仅约为传统N-R方法的四分之一，在弥补现有数据驱动潮流计算方法缺陷的同时保留了其计算速度快的优势。