基于FPGA的移动机器人SNNs走廊场景分类器

王睿轶,王秀青,刘万明,王永吉,叶晓雅

(1.河北师范大学 计算机与网络空间安全学院,河北 石家庄 050024;2.河北省网络与信息安全重点实验室,河北 石家庄 050024;3.河北省供应链大数据分析与数据安全工程研究中心,河北 石家庄 050024;4.河北师范大学 中燃工学院,河北 石家庄 050024;5.中国科学院 软件研究所,北京 100190)

0 引 言

第三代神经网络——脉冲神经网络(Spiking Neural Networks,SNNs)[1-3]通过独立的尖脉冲(Spikes)传递信息,将时空信息同时融于网络中,不仅比前两代神经网络具有更好的生物似真性,而且更适于用硬件实现。近年来,作为重要科技前沿的脑科学和类脑智能技术引起了国际学术界的广泛关注,各国投入巨资启动了脑研究计划。类脑计算是脑研究计划的重要方面之一,SNNs以其独有的生物似真性成为类脑计算的主要工具。神经形态芯片是类脑计算的重要研究内容之一,神经网络的硬件实现是神经形态芯片实现的基础,也是各种神经网络算法工程实用化的关键环节,进行SNNs硬件实现研究具有重要意义。基于硬件实现的SNNs解决方案,具有信息处理速度快、能耗低,适于实际应用等特点,成为当今研究的热点。

国外在SNNs硬件实现方面的研究成果显著。2013年,瑞士苏黎世大学与联邦理工学院成功研制出基于SNNs的脑神经形态芯片[4]。2014年,IBM公司推出运行功耗极低的TrueNorth芯片[5],英国曼彻斯特大学开发了SpiNNaker芯片[6],美国斯坦福大学研制出了神经栅格芯片系统[7]。2020年,英特尔发布了神经形态计算系统─Pohoiki Springs,该系统可提供1亿个脉冲神经元进行任务处理。2021年,Nguyen等人[8]在芯片上实现了基于脉冲时间依赖可塑性(Spike-Timing-Dependent Plasticity,STDP)的深度SNNs学习方法,较基于软件的基线SNNs学习方案速度提升2.1倍、能耗减少64%。2022年,Panchapakesan等人[9]提出了基于率编码的SyncNN方法,该方法相较传统卷积神经网络(Convolutional Neural Networks,CNNs)在MNIST数据集上的训练速度提高2.26倍。

国内虽然对SNNs硬件实现的研究起步较晚,但也取得了一定成果。2016年,浙江大学顾宗华团队设计出国内首款支持SNNs的类脑芯片——达尔文芯片[10],并成功应用于类脑计算和模式识别等任务中。2017年,Sun等人[11]提出了一种用于视觉信息特征提取的脉冲神经网络,并在FPGA上进行了实现。2019年,清华大学类脑计算研究中心施路平团队提出了符合脑科学基本规律、可同时支持ANNs和SNNs的新型类脑计算架构——异构融合的天机类脑计算芯片架构[12]。2020年,Zhang等人[13]提出一种基于FPGA应用于图像分类的低成本、高性能的SNNs实现方案,与软件实现相比运行速度提高了908 578倍。2021年,Wang等人[14]利用加速体系结构提出一种基于FPGA的SNNs,并采用逼近式加法器实现该架构,与前期相关工作相比ALUT降低28%、能耗减少29%。

SNNs能同时融入时空信息的特点,使其成功应用于机器人环境感知[15-16]和控制[17-21]等领域,如:2018年,Garcia等人[15]基于STDP展开了人形机器人视觉注意力的研究。2020年,Tang等人[17]提出一种基于SNNs的移动机器人导航控制方法。2021年,Lu等人[18]提出一种基于STDP的移动机器人避障策略。2022年,Azimirad等人[19]提出一种基于CNNs和SNNs的机器人环境感知和控制系统。虽然类脑芯片已取得了一定进展,但SNNs神经形态芯片在机器人领域的应用仍有待进一步发展,很多面对机器人的类脑计算方法距离实际工程应用还有较大差距。例如,文献[19]中控制策略算法需要在上位PC机中完成,再将控制命令发送给机器人执行。神经形态芯片和集成在芯片中的神经控制器的使用,除提高机器人自主性、加速机器人系统的信息处理和执行速度外,还使整个机器人系统轻量化,更便于实际使用。

现场可编程门阵列(Field Programmable Gate Array,FPGA)可以通过数据并行处理和运算加速来提高实际信息处理的能力[22-24]。该文提出一种基于FPGA的逼近式脉冲积分点火(Integrate-and-Fire,IAF)神经元模型硬件实现方案,基于IAF神经元模型实现了基于FPGA的移动机器人SNNs走廊场景分类器。此分类器可安置于机器人本体,使用的硬件资源少,结构简单,使用方便。所提基于FPGA的SNNs走廊场景分类器利用机器人超声传感器采集环境信息,受外界因素影响小,即使在光照不足或黑暗的走廊场景中依然能够准确、快速地进行走廊场景识别。仿真及实验结果验证了所提基于FPGA的移动机器人SNNs走廊场景分类器的有效性。

1 脉冲神经网络

1.1 积分点火模型

积分点火神经元模型是脉冲神经元模型中广为使用的一种阈值点火模型,是脉冲响应模型(Spike Response Model,SRM)[1]的特例。IAF神经元模型原理如图1和公式(1)所示[1]。电路中输入电流(I)分为两部分:一部分流向电阻(R);另一部分给电容(C)充电。当电容(C)两侧电压超过阈值(ϑ)时,神经元发放脉冲。

(1)

其中,ui表示神经元i膜电压值,τm=RC是神经元膜时间常数。由公式(1),IAF模型亦可如式(2)所示[1]。

(2)

(3)

(4)

其中,ϑ为点火阈值,urst为静息期电压,τm,τs为时间常数,H(s)为阶跃函数。

1.2 脉冲时延编码

时延编码(Latency Coding)通过不同的脉冲时延表示输入神经元的刺激信号的强弱[1]:刺激信号越弱,神经元发放脉冲时刻越晚、时延越长;刺激信号越强,神经元输出脉冲时刻越早、脉冲时延越短。

2 移动机器人SNNs走廊场景分类器的FPGA实现

2.1 基于SNNs的移动机器人走廊场景分类器的基本原理

走廊环境是室内移动机器人常见的结构化场景,准确感知走廊环境,对实现移动机器人的自主性具有重要意义。文献[21]针对7种常见的结构化走廊场景,提出基于超声传感信息的移动机器人SNNs走廊场景分类器(超声传感器工作原理及16个超声传感器在移动机器人本体中的分布见文献[21])。7种常见的结构化走廊场景如图2所示,图2(a)～(g)分别代表走廊场景1～7。SNNs拓扑结构如图3所示,具体工作原理及相应FPGA实现方案见2.2.1～2.2.3。

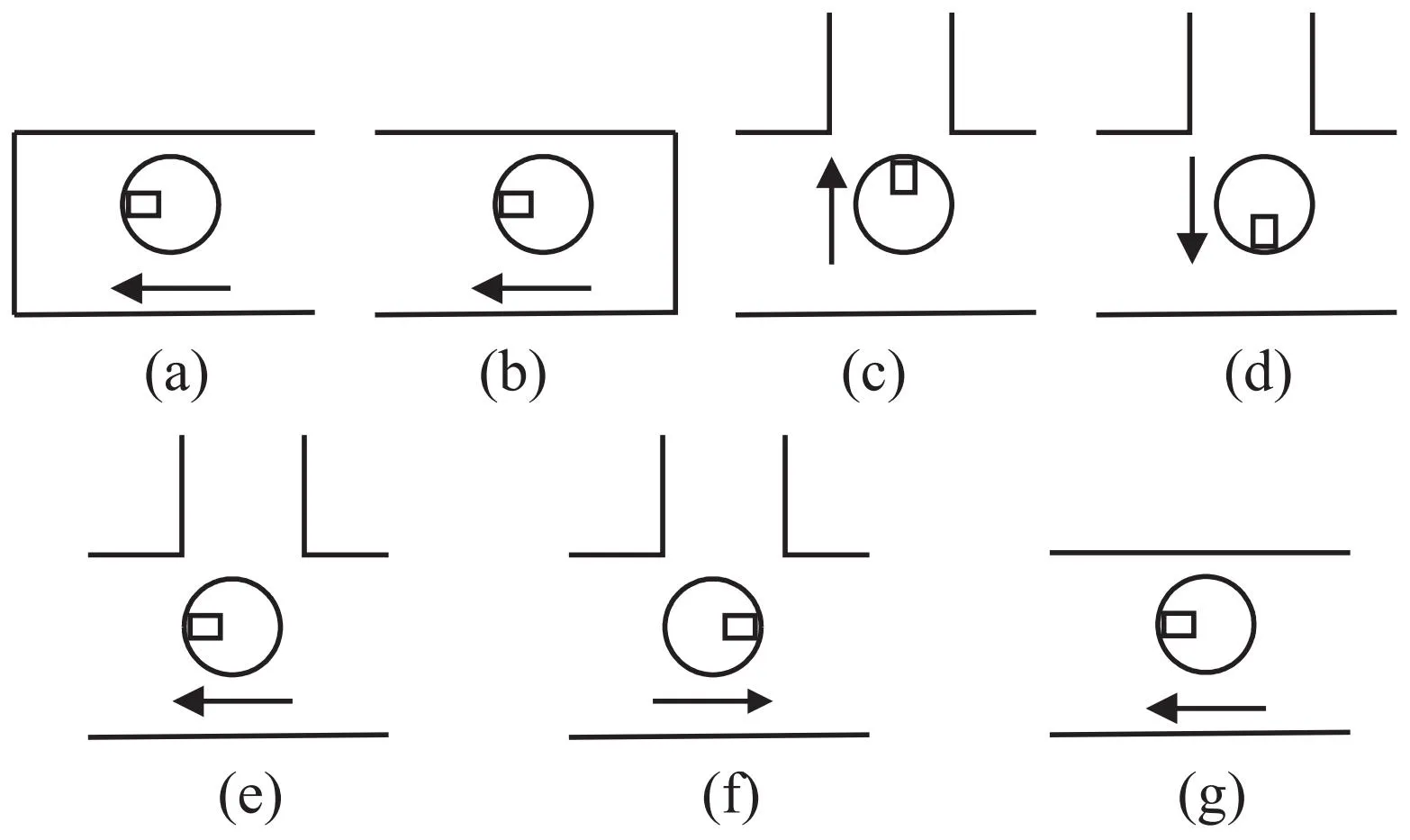
图2 常见的7种走廊场景

图3 移动机器人走廊场景分类器中SNNs拓扑结构

第1层为输入层,由sn×n个输入神经元组成。其中sn为机器人本体超声传感器环中的超声传感器个数,n为在某走廊场景中n个连续时刻采集的n组超声传感器信息。

第2层为隐含层,有sn×n×ni个神经元。第1层神经元到第2层神经元的连接权值均为w1(i1,j1)=1,其中j1为输入层神经元序号,j1=1,2,…,sn×n,i1为隐含层神经元序号,i1=1,2,…,sn×n×ni,ni为待分类走廊场景个数。

第3层为输出层,有ni个输出神经元。第2层神经元到第3层神经元的连接权值均为w2(i2,j2)=1,其中j2为隐含层神经元序号,j2=1,2,…,sn×n×ni,i2为输出层神经元序号,i2=1,2,…,ni。输出层神经元之间为侧向抑制联结,采用“赢者通吃(Winner-Takes-All,WTA)”的原则。

2.2 移动机器人SNNs走廊场景分类器的FPGA实现原理

利用FPGA对文献[21]中移动机器人SNNs走廊场景分类器进行硬件实现,具体原理如图4所示。将移动机器人采集的超声传感器信息进行脉冲编码后输入所设计的基于FPGA的SNNs走廊场景分类器中,通过SNNs的脉冲输出模式判断移动机器人所处的走廊场景,采用硬件描述语言(Verilog HDL)设计并实现了图4各模块的相应功能。

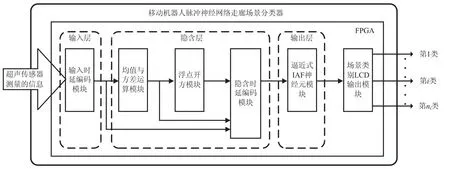
图4 基于FPGA的移动机器人SNNs走廊场景分类器的实现原理

(1)SNNs输入层硬件实现由输入时延编码模块(input_layer_latency_coding)完成(详见2.2.1节);

(2)SNNs隐含层的硬件实现由均值与方差运算模块(mean_variance)、浮点开方模块(floating_square_root)和隐含时延编码模块(hidden_layer_latency_coding)3个功能模块实现(详见2.2.2节);

(3)输出层由逼近式IAF神经元模块(approximate_iaf_neuron)实现。该模块实现了基于FPGA的逼近式脉冲积分点火神经元模型(详见2.2.3节)并输出相应于不同走廊场景的脉冲模式,通过输出脉冲模式识别走廊场景类别;

(4)FPGA将所得走廊场景的识别结果提供给移动机器人控制器进行下一步任务决策的同时,由场景类别LCD输出模块(scene_classification_lcd_output)通过LCD屏显示当前机器人所处走廊场景信息。

2.2.1 输入层的FPGA实现

输入时延编码模块原理:

将移动机器人在走廊场景中连续测得的n组超声传感信息经过脉冲时延编码后构造融合向量,作为输入层脉冲神经元的输入。

移动机器人超声传感信息编码成脉冲时延编码的具体过程如下:

(1)超声传感器信息的脉冲时延编码为:

(5)

其中,Twin为脉冲编码的时间窗,在此设为20 ms。xij(m)为超声传感器在第i个走廊场景的第j(j=1,2,…,14)组测量信息中第m(m=1,2,…,16)个超声传感器的测量值。max(x)为超声传感器的最大测量范围,取值为4 000 mm。Dij(m)为输出的脉冲时延编码。

(2)SNNs输入层融合输入向量为Dik。

Dik=[dik,di(k+1),…,di(k+n-1)]T

(6)

其中,i为待分类走廊场景(i=1,2,…,7),k为某走廊场景中输入数据的组数(k=1,2,…,5),dik为第i个走廊场景中第k个时刻的16个超声传感器测量信息的脉冲时延编码(dik=[Dik(1),Dik(2),…,Dik(m)]),n为在走廊场景中采用n个连续时刻采集的超声传感器信息构造融合向量的组数(n=3),融合向量的构造见文献[21]。

输入时延编码模块的FPGA实现:

在对SNNs进行硬件实现时,采用硬件描述语言编程:为减少FPGA硬件使用资源、提高运算速度和计算精度,算术运算器均采用32位单精度浮点数,其中整数部分用高12位二进制数代表,小数部分用低10位二进制数代表. 对超声传感器测量信息进行预处理后用Verilog HDL编程实现公式(5),具体实现如算法1所示:

算法1:输入时延编码模块的FPGA实现算法

输入:整个输入时延编码模块的仿真时间(Tsimulation)
输入层神经元数量(Nneuron)
超声传感器测量信息(xij(m))

输出:时延编码(Dij(m))

变量:时延编码的时间窗长(Twin)
超声传感器的最大测量范围(max(x))

(1) FORtsimFROM 0 TOTsimulation

(2) FORnneuronFROM 0 TONneuron

(3) IF(xij(m)==max(x))

(4)Dij(m)=0

(5) ELSE

为保证运算精度,提出数据扩大再缩小的运算方法,如步骤6中首先把xij(m)扩大210,然后除以max(x),再模除1 024进行缩放。取低10位二进制数表示小数部分可满足使用要求。

2.2.2 隐含层的FPGA实现

隐含层工作原理:

由于第1层神经元到第2层神经元的连接权值均为w1(i1,j1)=1,输入层的脉冲时延编码经过联结突触输入到隐含层。隐含层有着将输入数据向聚类中心汇集的作用。

在第i个走廊场景中分别采集l组超声传感器测量信息,计算该组脉冲编码的均值(μi)和方差(σi)。

(7)

(8)

其中,dij为第i个走廊场景中第j组超声传感器测量信息的脉冲时延编码,l为超声传感器测量组数。

隐含层中神经元的输出如式(9)所示:

(9)

令

td(j)=O2(16×n×(i-1)+k)

(10)

其中,td(j)(j=1,2,…,sn×n×ni)为隐含层第j个脉冲神经元的时延编码。

均值与方差运算模块的FPGA实现:

利用FPGA,采用硬件描述语言编程实现公式(7)的均值计算:对第i个走廊场景中在连续时刻采集的l组超声传感器测量信息(dij)进行连加运算,然后利用除法器对求和结果与l相除取其平均,实现均值运算的硬件实现。

(11)

浮点开方模块的FPGA实现:

浮点开方模块利用逐位循环开方算法的基本原理进行硬件实现。逐位循环(Digit-Recurrence)开方算法[25-26]是一种类似于试平方根的手算方法,其原理为:通过时钟周期不断迭代,利用折半遍历比较,计算差值不断去逼近真实值,最终判断最接近的根即为开方结果。

隐含时延编码模块的FPGA实现:

通过输入时延编码模块、隐含层均值与方差运算模块和隐含层浮点开方模块分别计算出输入时延编码、均值和方差的结果,采用硬件描述语言编程来完成隐含时延编码模块的FPGA硬件实现。公式(9)计算结果有2种情况,如公式(12)所示。

(12)

为保证计算精度问题,隐含层的输出由2部分组成:

(1)整数部分:因运算出的隐含时延编码的高10位均为0,所以可利用移位运算符左移10位,也就是被移位的数据高10位0被丢弃,而低10位固定补0作为小数部分;

(2)小数部分:输入时延编码与各个均值用减法器连接后扩大210,再除以方差,运算结果用1 024取余作为小数部分。

最终,将其2部分直接相加即可得到隐含层神经元输出的脉冲时延编码值。

隐含时延编码模块FPGA实现算法如下:

算法2:隐含时延编码模块的FPGA实现算法

输入:整个隐含时延编码模块的仿真时间(Tsimulation)
隐含层神经元数量(Nneuron)
超声传感器测量信息(xij(m))
输入时延编码(dik)
隐含层均值(μi)
隐含层方差(σi)

输出:隐含时延编码(td)

变量:超声传感器的最大测量范围(max(x))

(1) FORtsimFROM 0 TOTsimulation

(2) FORnneuronFROM 0 TONneuron

(3) IF(xij(m)==max(x))

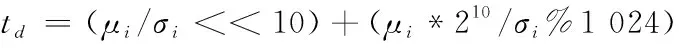
(5) ELSE IF(dik<μi)

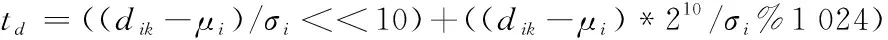
(7) ELSE

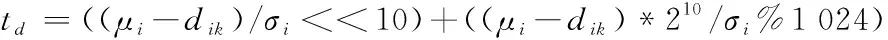
2.2.3 输出层的FPGA硬件实现

逼近式IAF神经元模块的硬件实现原理:

输出层神经元为IAF神经元。隐含层神经元的输出脉冲通过连接权值为w2(i2,j2)的联结突触将激活膜潜能(ui(t))输入到输出层IAF神经元。为了便于FPGA实现脉冲IAF神经元模型(见公式(2)),提出由公式(13)～(15)实现的逼近式IAF神经元模型来近似实现复杂IAF神经元模型:

ui(t)=w2(i2,j2)ε(t-td(j))

(13)

式中,t为输出层的时间窗长,核函数(ε)近似为:

(14)

其中,td(j)为隐含层输出脉冲的时延编码,膜时间常数τ=800 ms。

输出层逼近式IAF神经元的输出脉冲为:

(15)

其中,ϑ为脉冲神经元的点火阈值。

逼近式IAF神经元模块的FPGA实现:

输出层的逼近式IAF神经元模块实现了膜潜能计算和脉冲IAF神经元模型的相应功能,该模块的核心环节是核函数(ε)的计算。使用减法器和除法器分别计算逼近式IAF神经元模块中由隐含层神经元输出脉冲(该输出脉冲采用脉冲时延编码,详见2.2.2)提供的激活膜潜能值,该激活膜潜能值与逼近式IAF神经元点火阈值进行比较,来判断是否发放脉冲。该研究针对7个走廊场景进行分类,输出层设有对应的7个输出IAF神经元。如有一输出神经元先发放脉冲,因最先点火的神经元对其他神经元有侧向抑制作用,使得其他输出神经元不再点火。

逼近式IAF神经元模块的FPGA实现如下:

算法3:逼近式IAF神经元模块的FPGA实现算法

输入:整个逼近式IAF神经元模块的仿真时间(Tsimulation)
输出层神经元数量(Nneuron)
隐含层的时延编码(td(j))

输出:膜潜能(ui(t))
脉冲输出(Oi)

变量:膜时间常数(τ)
点火阈值(ϑ)

(1) FORtsimFROM 0 TOTsimulation

(2) FORnneuronFROM 0 TONneuron

(3)ui(t)=(t-td(j))/τ

(4) IF(ui(t)≤ϑ)

(5)Oi=1

(6) ELSE

(7)Oi=0

3 实验及结果分析

所提基于FPGA的移动机器人SNNs走廊场景分类器选用Altera公司Cyclone IV EP4CE10F17C8型号FPGA芯片,仿真环境为Modelsim,开发环境为Quartus II 13.1. 使用硬件描述语言(Verilog HDL)设计并实现了分类器中输入时延编码、均值与方差运算、浮点开方、隐含时延编码、逼近式IAF神经元和场景类别LCD输出模块的相应功能。下面对上述功能模块的时序仿真结果进行分析和讨论,其中clk和clr分别为系统时钟和复位信号,cnt为波形信号计数器。

实验中采用走廊场景分类准确率、分类器中FPGA所实现模块的计算精度,以及FPGA的资源利用率等指标对所提方法进行评价:(1)分类准确率:用于验证所提走廊场景分类器的有效性;(2)计算精度:SNNs走廊场景分类器FPGA实现的核心环节之一是用逼近式IAF神经元模型(见公式(13)～(15))来近似实现复杂脉冲IAF神经元模型。其中实现逼近式IAF神经元模型的FPGA相应模块的计算精度直接决定了最终IAF模型的实现精度。 实验中采用绝对误差和相对误差作为评价指标,反映各模块的计算准确程度;(3)资源利用率:指示所设计系统硬件资源使用量与可用量之比。利用率越低,意味着硬件系统的可拓展性资源越多,越便于未来系统功能的进一步升级和扩展。

3.1 输入时延编码模块的时序仿真及结果分析

输入时延编码模块的仿真结果如图5所示。超声传感器测量信息(xij(m))(见式(5))为输入信号(x_in),时延编码(dij(m))(见式(5))作为输出信号(T_delay_out)。图5实验结果表明:超声传感测量信息(x_in)为4 000 mm时,时延编码(T_delay_out)为0 ms;超声传感测量信息(x_in)为830 mm,800 mm时,时延编码(T_delay_out)分别为15.859 4 s,16.015 6 ms。实验结果的误差分析见表1,验证了FPGA实现脉冲时延编码方案的正确性。

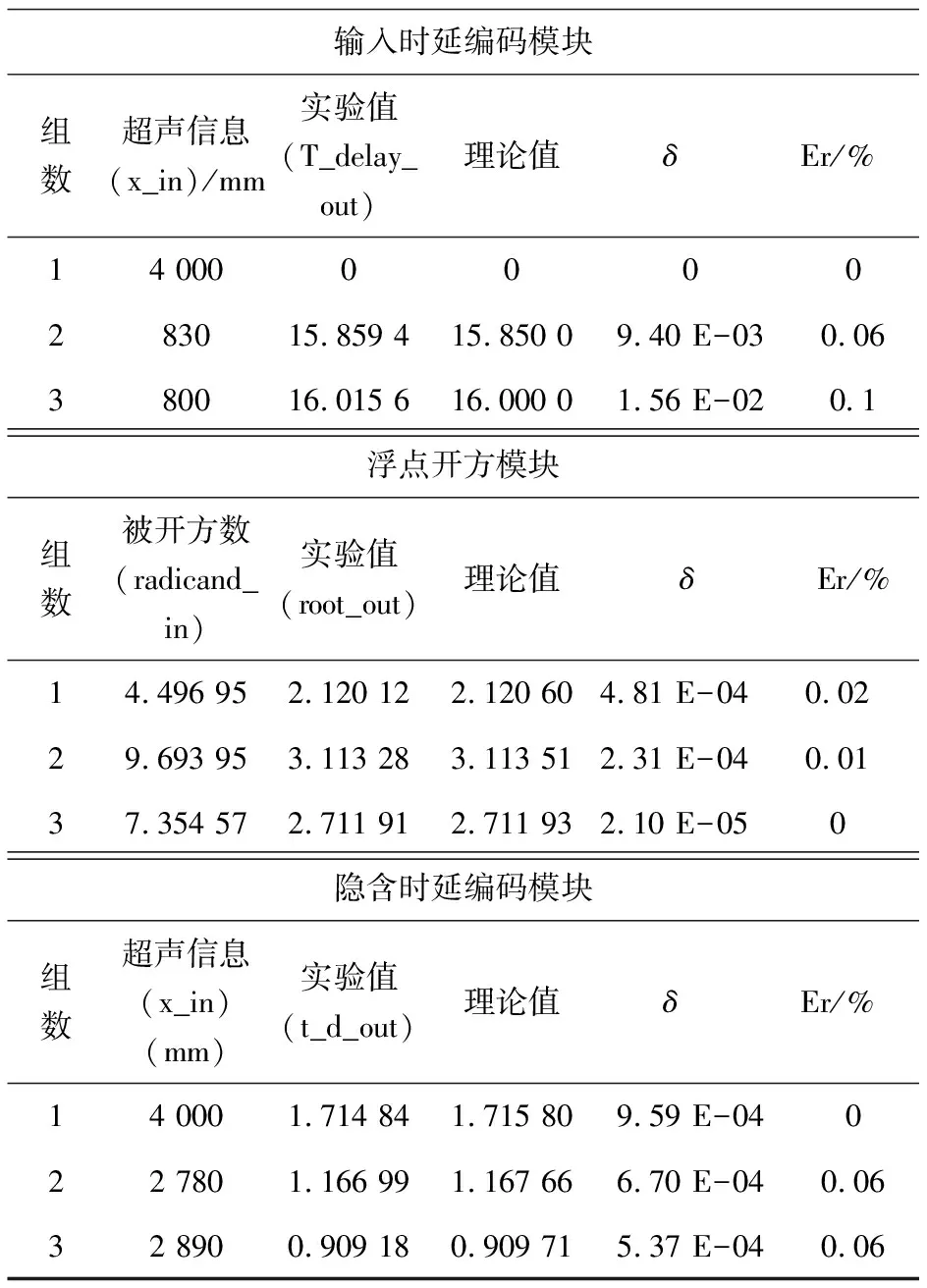
表1 各模块运算误差

图5 输入时延编码模块的仿真波形

3.2 浮点开方模块的时序仿真及结果分析

(a)被开方数的输入仿真波形

3.3 隐含时延编码模块的时序仿真及结果分析

隐含时延编码模块的仿真结果如图7所示。图中输入信号有:x_in,T_delay_in(分别代表超声传感器测量信息(xij(m))和时延编码(Dij(m)),见式(5)),mean_in(代表均值(μi),见式(7))和variance_in(代表方差(σi),见式(8))。输出信号(t_d_out)代表隐含层的时延编码(td(j),见式(10))。图7中超声传感器测量信息(x_in)为4 000 mm,时延编码(T_delay_in)为0 ms,均值(mean_in)为3.637 7和方差(variance_in)为2.120 12时,隐含层时延编码(t_d_out)输出为1.714 84 ms,时延编码模块的其他实验结果(见表1)亦在误差允许范围内。仿真实验结果表明基于FPGA的隐含时延编码方案正确有效。

图7 隐含时延编码模块的仿真波形

3.4 逼近式IAF神经元模块的时序仿真及结果分析

在逼近式IAF神经元模块的仿真实验中,设定计算时间轴长10 000 ms,包含m=5个时间窗,每一时间窗口(T)均为2 000 ms,点火阈值设置为119.908。时序仿真时输入第1类至第7类走廊场景采集的超声数据到所设计的FPGA走廊场景分类器中,得到7个输出神经元的膜潜能和输出脉冲模式,根据输出脉冲模式得出机器人当前所处走廊场景。当机器人所处第i个走廊场景时,输出层第i个神经元(Oi)的输入激活膜潜能最先达到点火阈值发放脉冲时,因为SNNs采用侧向抑制联结,此时输出层神经元仅有Oi点火,机器人所处走廊场景为1。因篇幅所限,在此仅给出了第1,7类2个走廊场景下的仿真结果(如图8所示)。逼近式IAF神经元模块的输出信号包括代表膜潜能(ui(t),见式(13))的信号(u_1-u_7)和代表脉冲输出(Oi(t),见式(15))信号的result_1-result_7。当图8(a)中输入信号为第1类走廊场景所采集的超声数据时,可以看到图中输出信号(result_1)为高电平,而信号(result_2-result_7)均为低电平,走廊场景分类器识别机器人位于走廊场景1;图8(b)中输入信号为第7类走廊场景所采集的超声数据,result_7为高电平,result_1-result_6为低电平,走廊场景分类器识别机器人位于走廊场景7。

(a)输入第1类走廊场景的超声数据时,输出神经元的膜潜能和输出脉冲

图8实验结果表明,当机器人位于第1和7类走廊场景时,将采集到的相应走廊场景超声传感器数据输入到所设计的基于FPGA的走廊场景分类器中,均能正确分类。实验结果证明,采用脉冲时延编码,结合所提逼近式脉冲IAF神经元模型,实现了走廊场景的识别。

3.5 FPGA中各模块运算误差分析

在利用FPGA实现走廊场景分类器功能时,需要FPGA实现相应的计算均值、方差、开方等各种运算。为保证有效实现所设计SNNs的相应功能,需要基于FPGA的运算模块达到所需的计算精度。图4中输入层、隐含层、输出层各模块采用FPGA实现时,产生的误差有:

(1)输入信号转换产生的误差。在进行FPGA实现之前,需将超声传感器信息转换成定点型数据,这使得实际数据中小数部分被截断而带来误差;

(2)运算结果溢出产生的误差。基于FPGA的SNNs在进行基本数据运算时,数据可能因位宽不足导致溢出,计算出的数据需要截断,截断数据会引起相应的计算误差。

为了减少运算误差,提出了基于SNNs的数据扩大再缩小的运算方法(见2.2.1节),以保证FPGA实现的运算精度。各模块运算误差如表1所示,其中δ和Er分别表示绝对误差和相对误差。通过表1可知,各模块计算的绝对误差最大在10-4数量级,相对误差在10-3数量级以下。实验结果证明了所提方法能够满足分类器所需的精度要求。

3.6 走廊场景分类实验结果

图9为FPGA通过RGB TFT-LCD接口在机器人本体上的LCD液晶屏中显示走廊场景分类器输出的移动机器人当前所处走廊场景类别及所对应的走廊场景示意图,走廊场景示意图具体如图2所示。

图9 基于FPGA的SNNs走廊场景分类器实验结果

由于脉冲神经网络的使用,基于FPGA的移动机器人走廊场景分类器具有占用芯片资源少、可扩展性好、计算效率高的优点,其中LE的占用率仅10%(1 067/10 320)。

所提基于FPGA的移动机器人SNNs走廊场景分类器的分类准确率为92.86%。对于同样的走廊场景识别任务,采用相同的超声传感信息,文献[21]中基于BP神经网络的软件实现方法分类准确率为82%,文献[16]中基于阶次编码和NeuCube模型的SNNs软件实现方法的分类准确率为92.86%,文献[21]中基于时延编码和IAF神经元模型的SNNs方法的分类准确率为94%。所提方法是文献[21]SNNs软件方法的硬件实现,二者分类准确率仅相差1.14%。实验结果表明,所提SNNs硬件实现方案可以保证SNNs走廊场景分类的有效性,且基于FPGA的SNNs走廊场景分类器更适于实际使用,该研究有助于SNNs神经形态芯片在机器人领域的应用。

4 结束语

实验部分FPGA实现的输入时延编码、均值与方差运算、浮点开方、隐含时延编码和逼近式IAF神经元模块的时序仿真结果及相应误差分析表明,各模块计算的绝对误差最大在10-4数量级,相对误差在10-3数量级以下,满足了分类器所需的运算精度要求,利用FPGA有效地实现了脉冲IAF神经元模型。此外,基于FPGA的移动机器人SNNs走廊场景分类器的分类准确率为92.86%,验证了所提方法对于走廊场景识别的有效性。在FPGA硬件资源使用方面,所提走廊场景分类器的LE利用率仅10%,说明此分类器具有良好的扩展性能。

所设计的走廊场景分类器不受光照条件的影响,需要的传感器信息少、结构简单易于实施。该研究可提高移动机器人的环境感知能力,为脉冲神经网络的实用化提供了解决思路,为类脑神经形态芯片的发展提供了有益参考。信息处理速度快、能耗低、轻量化的神经机器人将是机器人技术未来发展方向之一,该研究亦为未来实现神经机器人奠定了基础。