结构化教学，推动学习“自能化”

苏丹

［摘 要］数学学习的本质是将数学知识结构转变为自身认知结构的过程。为了更好实现这个转化，教师需要对课程内容进行结构化设计，梳理主题和脉络，让学习化繁为简，真正实现学习“自能化”。文章以“梯形的面积计算”一课为例，阐述如何从教学目标的整体性、知识之间的关联性、思想方法的一致性、练习设计的系统性四个方面进行结构化教学。

［关键词］梯形；结构化；学习“自能化”

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2023）26-0069-03

数学来自人类劳动和探索客观世界的具体实践，从古人结绳计数到质能方程，数学知识是从具体实践中抽象而来的，具有结构化属性。数学学习的本质是让数学知识结构与认知结构相互作用，将数学知识结构转化为自身认知结构的过程。

学生建立怎样的认知结构，取决于教师为他们提供怎样的信息与知识。因此，教师首先要考虑课程内容的结构化设计。

从“结构”的角度来展开教学，既能帮助学生建立数学知识间的逻辑联系，又能帮助学生把握内容的实质。有个成语叫一叶知秋，因为有了结构化的知识体系，所以可以从局部扩展到整体，如“一叶知秋”一般，从一片树叶知道季节的交替，透过现象看本质。结构化教学正是希望培养学生的结构化认知能力，使学生实现知识、方法的自主生长，从而拥有“一叶知秋”的能力。下面以“梯形的面积计算”一课为例，谈谈如何进行结构化教学。

一、把握教学目标的整体性

结构化教学是要学生通过回顾联想、类比提升、反思积累，逐步将知识结构内化，培养学生对知识结构的整体感知。这需要教师在组织结构化学习时，整体把握课时内容的教学价值，厘清某个领域知识的基本结构，结合版块整体目标，制订合理、有效的课时目标。

多边形面积计算教学有相同的模式，都是让学生在观察、操作、比较、推理等活动中探索平面图形面积的计算方法。整个过程都围绕“转化”这一核心思想展开，在探究平行四边形的面积时，学生初次尝试运用切割、平移等方法进行图形的转化，初步感受转化思想。紧接着探索三角形的面积公式时，学生学会运用转化思想来计算三角形的面积，体验转化的意义。在探索梯形面积公式时，有了前两节课的学习经验，学生自主迁移学习方法，也就实现了学习“自能化”。

另外，还可以对平面图形面积的计算方法进行结构化，双向沟通平面图形之间的联系：把梯形转化成其他平面图形，再推导出梯形的面积公式；梯形的面积公式也服务于其他平面图形，可用来计算其他平面图形的面积。学生在感知知识整体性和结构化的同时，体会数学抽象、逻辑推理、数学建模等思想方法，自主获得探究同一类知识的学习路径，培养核心素养。

教学“梯形的面积计算”一课时，笔者设计了以下教学目标。

1.在操作、观察的过程中自主探究梯形的面积公式，培养自主学习的意识，发展空间观念，提升学科素养。

2.在比较、分析、推理等数学活动中建立梯形的面积公式模型，并能利用公式解决生活中的实际问题，体会转化的意义和价值，发展逻辑思维。

3.沟通梯形与其他平面图形面积公式之间的联系，感受数学知识的结构美。

二、挖掘知识之间的关联性

数学中的每一个知识点不是单独存在的，都属于某一个知识体系，考虑到学生的认知规律及其他因素，教材编排时切断了一些知识链，使知识点犹如“散落的珍珠”分散在不同的学段里。因此，教师需要沟通知识间的内在联系，将分散的知识点串成知识链，编织成知识层级，再将知识层级建构成知识结构，从元素到系统，从局部到整体，让学生从全局看清知识结构体系的全貌，形成“从结构的角度把握事物本质”的结构化思维。

[片段1]

师：同学们，前两节课我们一起研究了平行四边形、三角形的面积计算方法，我们是怎样探索的？

生1：把平行四边形分割、平移，转化成长方形，转化前后图形的面积不变。

生2：把两个完全相同的三角形拼成一个平行四边形，可以发现其中一个三角形的面积是平行四边形面积的一半。

师：探索平行四边形、三角形面积公式的过程，有什么相同之处？

生3：都把新知转化成了旧知。

师（出示图1）：是的，转化是数学学习中非常重要的数学思想。那么，你打算把梯形转化成什么图形，再求它的面积？试着用分割、添补、平移、旋转等方法，把梯形转化成已学过的平面图形吧。

梯形的面积与前两节课（平行四边形的面积、三角形的面積）内容相近、结构相同，都可以通过割补、添补、平移、旋转等方式把未知转化成已知，从而探索面积计算方法。课堂上教师通过复习、回顾激发学生的已有经验，借助思维导图沟通各平面图形之间的联系，以“你打算把梯形转化成什么图形？”为主线，利用新旧知识之间的共通性，引导学生展开迁移性学习，使知识具有自主生长的活力。

三、紧扣思想方法的一致性

数学学习的精髓不只在于习得几个公式、记住几个定律，更重要的是形成数学思想方法。成熟的数学思想方法是通向解决问题的桥梁，连接已知和未知，沟通理论与实践。教师要善于将数学思想方法以及本质规律进行有效迁移，将其延伸或者拓展到相似问题的解决过程中，形成新的解题思路，从而得到新的数学感悟和体会，建构新的知识结构化。

[片段2]

师：运用转化思想，你把梯形转化成了什么图形？转化前后的图形面积有怎样的关系？你还有什么发现？怎样求梯形的面积？

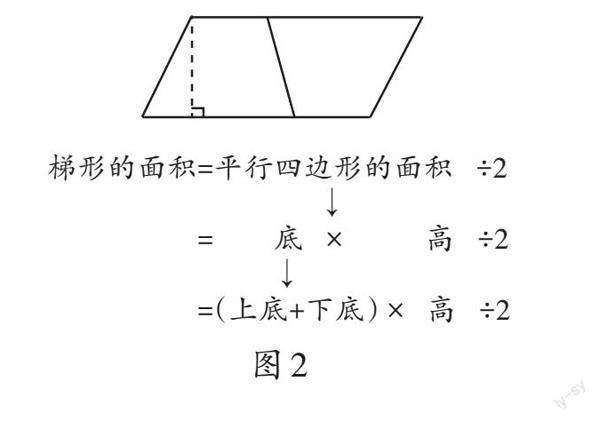
学生自主探究后汇报交流（如图2、图3）：

师：比较同学们的探究过程，有什么相同和不同的地方？

生1：得到的梯形面积公式相同。

生2：都运用了转化的策略。

生3：公式中都有“[÷]2”。

师：同学们观察得真仔细，用添补法（如图2），梯形面积是平行四边形的一半，因此梯形的面积公式中有“[÷]2”。为什么用分割法时（如图3）也要“[÷]2”呢？

生4：计算图3中三角形的面积时就要“[÷]2”。

师：是呀，不同的方法，“[÷]2”表示的意义也不同，但最终都成功把梯形转化成了已学过的平面图形，并得到了相同的梯形面积公式。

“多边形面积”的教学重点在于让学生感悟转化思想，思想是一致的，但转化方法有所不同。课堂上学生通过添补、分割等不同方法，把梯形转化成了已学过的平面图形，积累了丰富的活动经验，感受了转化方法的多样性，再次沟通了梯形与其他平面图形之间的联系。转化后，教师通过“为什么要‘÷2’？”这一问题渗透“倍积变形”“等积变形”的数学思想，激发学生透过现象挖掘本质，通过推理对比发现用不同的方法推导公式时，“[÷]2”的意义是不一样的，使学生进一步感悟“虽然转化方法不同，但结果相同”。整个过程中，教师给学生提供了充分的探索空间，有效提升了学生思维的灵活性，促进学生的思维迈向高阶。

四、聚焦练习设计的系统性

有层次的练习能在巩固本节课所学知识的同时，厘清知识之间的联系，在“变”与“不变”中凸显不同面积公式中相同的原理，将分散的知识用结构化的思维穿成一条条线，结成一张张网，真正有效地促进学生对知识的掌握和理解。

生1：一样大。

师：为什么？把你的想法和大家分享一下。

生1：因为三个梯形上底与下底的和都等于10，它们的高又是相等的，所以面积也相等。

师：这三个梯形虽然形状不同，但它们上底加下底的和相等，高也相等，我们说这三个梯形是等底等高的。等底等高的情况下，它们的面积也相等。你还能说出一些与这三个梯形的高相等、面积也相等的图形吗？

生2：上底是1米，下底是9米，高是5米的梯形。

生3：底是5米，高是5米的平行四边形。

生4：底是10米，高是5米的三角形。

师：同学们找到了这么多图形，它们的面积都相等吗？我们通过计算验证一下。（学生口答验证）

师：为什么平行四边形、三角形的面积也可以用梯形的面积公式来计算呢？看了接下来的动画你就能明白啦。

动画演示：梯形的上底变大，当a=b（a是上底，b是下底）时，梯形就变成了平行四边形，其面积公式可写为S平行四边形=（a+b）×h÷2=（a+a）×h÷2=2a×h÷2=a×h。

动画演示：梯形的上底变小，当a=0时，梯形就变成了三角形，其面积公式可写为S三角形=（a+b）×h÷2=（0+b）×h÷2=b×h÷2。

课堂上教师精心设计了三个形状不同但面积相等的梯形，通过数形结合帮助学生明确：在高相等的情况下，只要“上底与下底的和”相等，那么这些梯形的面积也相等。以此为基础，对于问题“你还能说出一些与这三个梯形的高相等、面积也相等的图形吗？”，学生能想到的就是高不变，上底与下底的和是10米的图形。

这一环节的设计在更高层面上将三种图形之间的联系进行了沟通，提炼出共同的本质以提升学生的迁移能力，并通过运动变化展示图形的转化过程。通过推理沟通三种图形的面积公式，凸显它们之间的内在关联，推导出可以相互转化的多边形的面积公式。这就是知识的结构化，具有内联沟通、举一反三、融會贯通的价值。

结构化教学向学生展示了知识之间是有联系的，是有机的整体，有先后逻辑，有主次关系，学生看到了整个结构和生长的过程，才能理解数学从具体到抽象的演变，了解其内在逻辑与意义。有了教学目标、内容、思想方法、练习的结构化设计，学生的学习方法、思维能力都向着结构化的方向发展和完善，才能实现真正的学习“自能化”，从而推动数学素养自主生长。

［ 参 考 文 献 ］

[1] 许卫兵.小学数学整体建构教学[M].上海：上海教育出版社，2022：73-102.

[2] 李雪梅.结构化建构概念   系统化发展学生思维：以“认识负数”教学为例[J].教育科学论坛，2021（10）：57-60.

[3] 朱俊华.小学数学单元整体教学重在结构关联[J].中小学教师培训，2021（4）：56-60.

（责编 黄 露）