振动荷载下不同级配的基床粗粒土填料孔隙连通性特征研究

王萌，于群丁, ，肖源杰, ，华文俊，李文奇

(1. 中南大学 土木工程学院，湖南 长沙，410075；2. 中铁第四勘察设计院集团有限公司 城市轨道与地下工程设计研究院，湖北 武汉，430063；3. 重载铁路工程结构教育部重点实验室(中南大学)，湖南 长沙，410075)

传统不透水材料及不透水路基路面结构的大规模应用直接或间接加剧了洪涝灾害和热岛效应等诸多问题。为有效应对全球变暖和极端天气，大力推进“海绵城市”建设意义重大[1-3]，其中，由级配碎石等粗粒土填料填筑而成的透水性基床是经济、环保的重要举措之一，因此，有必要深入研究基床粗粒土填料透水性能的优化和施工后长期保持技术。经振动压路机碾压填筑而成的基床通常具有较好的压实质量和施工后的服役性能[4]。为较好地模拟现场压路机的碾压作用，目前，粗粒土填料室内试样的制备也多采用振动压实方法[5-6]。新型耐久性、透水性基床对粗粒土填料的压实特性和其级配优化理论及设计成为近年来的研究热点[7-9]。杨孝攀等[10]针对砂砾料优化了其级配参数，即当曲率系数为1～10、不均匀系数大于5 且级配方程参数b和m分别介于0.7～0.9 和0.6～0.9 时，其干密度最大。张志红等[11]基于分形(fractal)理论和Furnas 方程提出了散体颗粒材料的级配优化F-F方程，并结合颗粒流算法验证了该方程对于砂土及碎石材料密实度的高效控制具有普适性。肖源杰等[12-15]基于一系列室内新型平板振动压实试验、动-静三轴试验、离散元数值模拟以及力学-经验法预估模型，提出了可综合考虑压实度、永久变形和渗透特性的透水性碎石填料级配优化设计方法。然而，现有研究大多专注于粗粒土填料级配优化及其压实质量等宏观研究，却忽视了级配对粗粒土填料振动压实后的三维孔隙连通性及透水性能的影响，无法确保路基基床的施工后渗透性能满足预期要求，因此，亟待针对此不足开展深入研究。

近年来，计算机断层扫描(CT)技术逐渐从医学领域拓展至其他相关领域用于微细观结构量化分析。李朋等[16]基于CT扫描试验分析了不溶物沉渣的孔隙尺寸及孔隙连通度，较好地评价了多夹层盐矿沉渣孔隙储气能力。杨欣欣等[17]利用显微CT 技术提取高温砂岩孔隙，发现随着温度降低，连通团体积增大，渗透率增大。张鹏伟等[18]建立了地下储层中岩土介质的孔隙结构模型，并开发了两相流计算模型以分析其相对渗透率。WANG等[19]利用X射线计算机断层扫描(XCT)技术研究了地下工程腐蚀水环境中防水片材的微细观孔隙组织，发现中孔和大孔对材料的孔隙率影响很大，孔隙率和孔隙连通性可作为评价防水片材抗渗性的关键指标。鉴于CT扫描技术在结构微细观分析方面尤其是在孔隙分析方面具有较大优势，国内外学者开始将其应用于路基路面材料的三维重建及孔隙提取[20-22]。如ZHANG 等[23]利用CT 技术重构了三维透水性混凝土，提取了其连通孔隙网络模型，采用计算流体力学方法开展了渗流模拟，得到了渗流速度与压力梯度的关系。ZHAO等[24]分析了沥青混合料中的渗流路径，将孔隙结构按照其在渗流行为发生过程中所产生的不同作用分为有效孔隙与无效孔隙，发现有效孔隙对沥青混合料的水文物理性质影响程度远远大于无效孔隙对其水文物理性质影响程度。叶加兵等[25]对比分析了玻璃球多孔介质和碎石料的孔隙结构，发现碎石料的连通度要小于玻璃球多孔介质的连通度。MADY等[26]采用XCT技术评估了孔隙(包括开孔和闭孔)的连通性对饱和导水率(Ks)的影响，发现孔隙连通性对Ks的影响接近于孔隙分布对Ks的影响。FERREIRA 等[27]研究了石灰含量对土壤内部孔隙的孔隙度、连通性、曲折度和分形维数等的影响，发现掺入石灰降低了粒径范围为1～2 mm的骨料总孔隙率，增加了孔隙的曲折度，降低了孔隙形态的分形维数，但孔隙连通性并未受石灰掺入的影响。可见，目前针对透水性材料细观渗透特性的研究主要集中于孔隙连通性，且以透水性水泥混凝土、沥青混凝土以及土壤等材料为主，却鲜有针对路基基床粗粒土填料振动压实后孔隙连通性的研究。

为此，本文作者首先设计G/S分别为1.0、1.8、2.5 的粗粒土填料，进而开展室内新型平板振动压实试验并依据干密度确定最优激振参数组合；其次，针对最优激振参数工况下的振动压实试样，利用高精度工业XCT 扫描技术获取其二维切片，结合图像处理技术和最大球算法等重构相应的三维球棍模型并量化其三维孔隙的连通性；最后，基于球棍模型模拟不同级配类型试样的三维渗流过程，并对比分析其渗流特征。

1 室内新型平板振动压实试验

1.1 试验材料

本文试验所用基床粗粒土填料源自于湖南长沙郊区某路基施工现场，填料的最大颗粒粒径为26.5 mm，其中碎石颗粒母岩为灰岩。本文采用肖源杰等[12-13,28-30]所提出的石砂质量比(G/S)，设计为1.0、1.8、2.5 这3 种不同类型的颗粒堆积结构(级配)，具体的级配设计理论和方法见文献[28-30]，试验级配方案及其参数见表1，级配曲线见图1。

图1 室内试验所采用的级配曲线Fig.1 Gradation curves used in laboratory tests

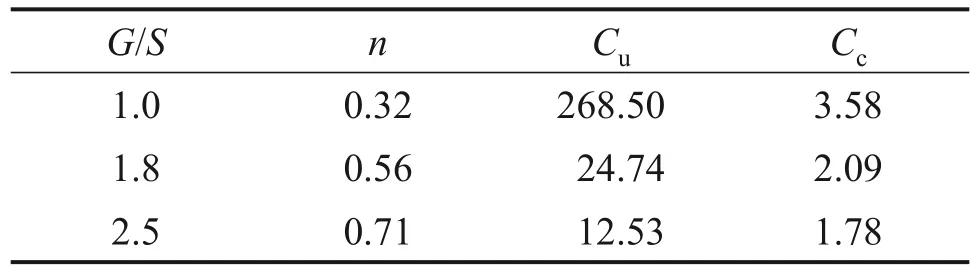
表1 室内试验级配设计方案及其参数Table 1 Gradation design scheme and related parameters of laboratory tests

1.2 新型平板振动压实试验

室内试验采用一种可实现双轴偏心振动的平板振动压实成型仪，对3 种不同G/S的粗粒土填料试样进行压实成型。考虑现场振动碾压的实际工况，本次试验采用的激振频率(F0)包括18、21、25、30 和35 Hz，激振力(f)包括700、1 400和2 800 N。为尽可能减少尺寸效应对振动压实结果的影响，试样的直径应大于填料最大颗粒粒径的5 倍，但受本文所采用的高精度工业XCT 扫描设备测试精度的限制，试样直径定为120 mm，约等于填料最大颗粒粒径的4.5倍，可较好地消除尺寸效应，保证试样的均匀性。

图2 所示为3 种不同G/S的填料试样压实后的干密度随激振频率和激振力的变化曲线。由图2(a)可知，对于不同G/S的填料，其干密度最大的激振频率均为25 Hz。由图2(b)可知：当激振力达到1 400 N 时，继续增大激振力对干密度的提高效果并不显著。因此，基床粗粒土填料平板振动压实的最优激振频率为25 Hz，较优的激振力为1 400 N。根据文献[13]，基床粗粒土填料的平板振动压实过程可分为3 个不同阶段(见图3)：压实[0，10) s 为第一阶段；压实[10，60) s 为第二阶段；压实[60，120) s为第三阶段。考虑到经济性和效率，可认为激振60 s后试样已达到较大密实度。因此，本文高精度工业XCT 扫描试验中的粗粒土填料试样均在上述最优激振参数组合(即激振频率为25 Hz 且激振力为1 400 N)下振动压实60 s。

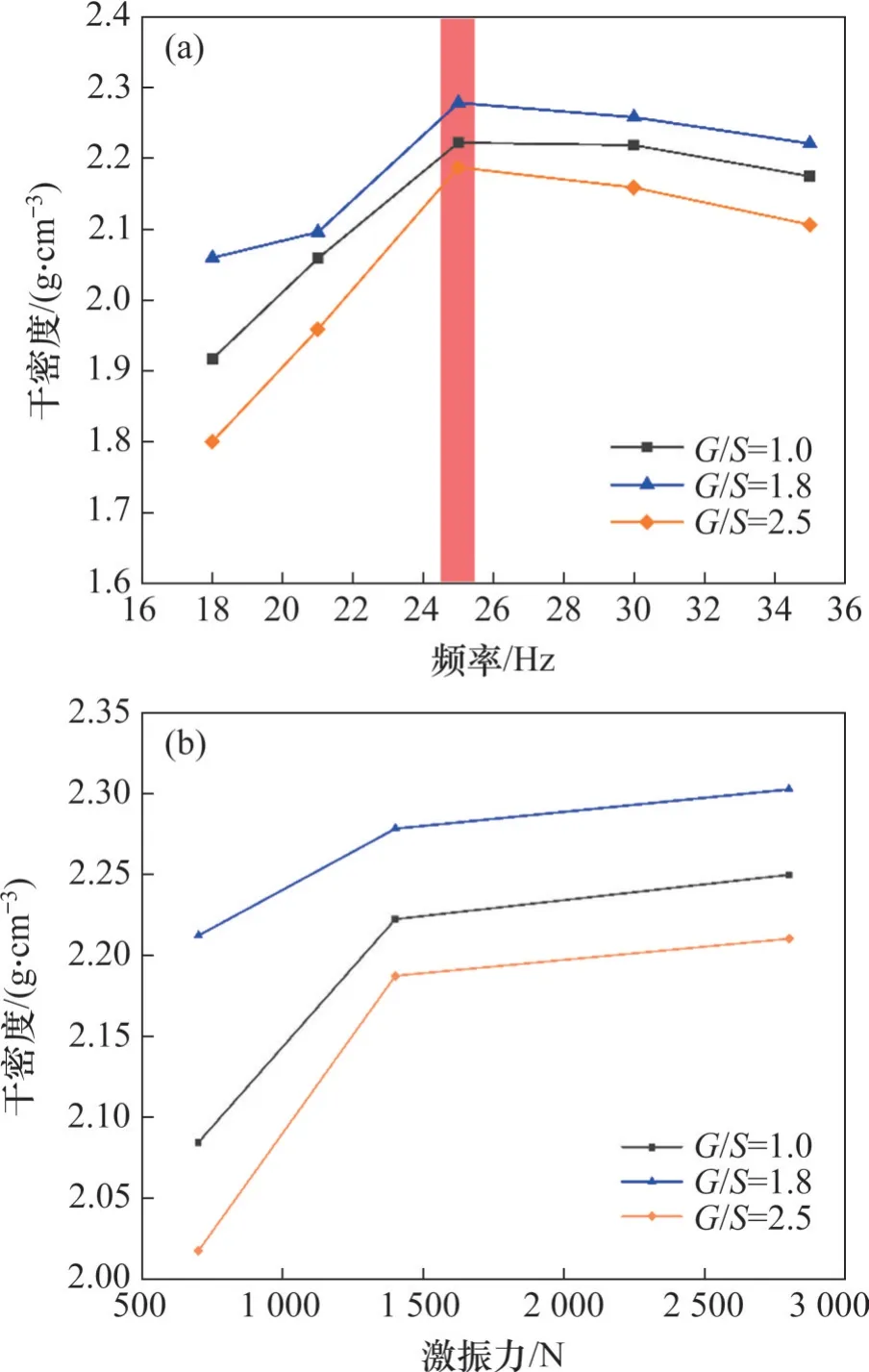
图2 不同G/S的填料试样平板压实试验干密度随激振频率及激振力变化曲线Fig. 2 Curves of achieved dry density versus vibratory frequency and force from laboratory vibratory plate compaction tests of unbound aggregate specimens with different G/S

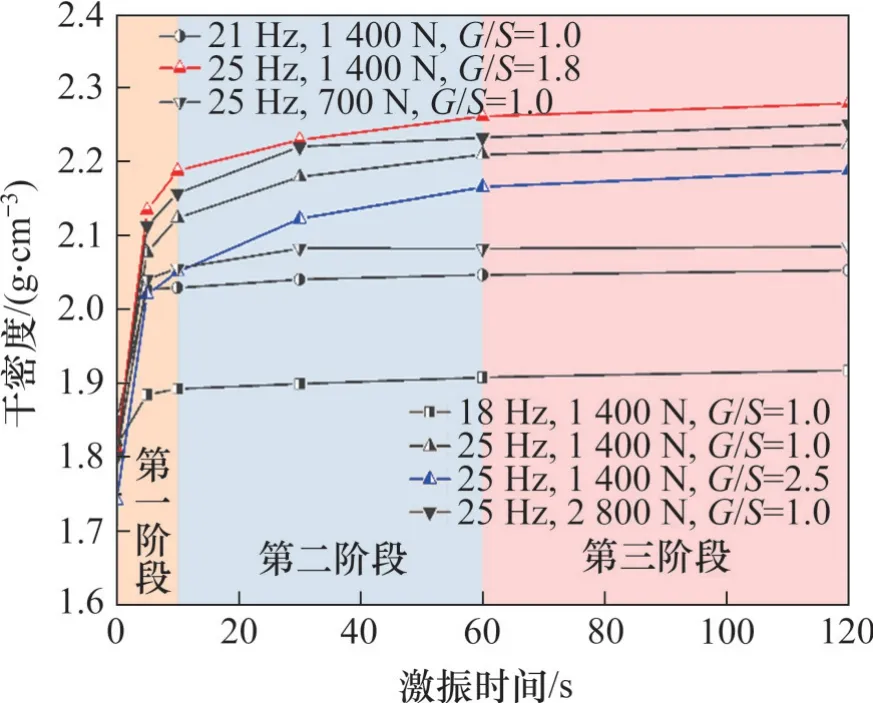
图3 室内平板击实试验填料试样干密度-时间关系曲线Fig. 3 Curves of achieved dry density versus vibration time from laboratory vibratory plate compaction tests of unbound aggregate specimens

2 基于XCT 的级配碎石填料三维孔隙重构及量化分析

本文采用Phoenxi v|tome x|s 型高精度工业XCT 扫描仪，扫描电压为420 kV，扫描电流为1.6 mA，探测器探测范围长为820 mm，分辨率为80 μm。本文以0.08 mm 的等间隔对不同G/S的粗粒土填料试样在振动压实60 s 后进行XCT 扫描以获取其三维微细观结构特征。

采用VG Studio Max三维重构分析软件将XCT扫描生成的粗粒土填料试样切片图像进行噪点去除、图像增强及平滑等数字图像处理操作，再按序列依次导入软件进行精确的三维重构，经三维重建后的数字模型可真实地反映填料内部的微细观结构。石砂质量比(G/S)为1.8的填料试样在最优激振工况(即激振频率为25 Hz和激振力为1 400 N)下压实60 s 后的填料试样及其三维重构模型见图4。

图4 G/S为1.8的填料试样在最优激振工况下振动压实后的实物图及其XCT扫描三维重构模型Fig. 4 Illustration of unbound aggregate specimen and reconstructed model from XCT scanning after laboratory vibratory plate compaction tests with G/S=1.8 under optimal vibratory conditions

基于XCT 扫描获取的三维重构模型，利用最大球算法及Avizo软件建立填料试样内部结构的球棍模型并用于虚拟试样的三维渗流模拟。最大球算法[23]的原理是选取填料内部孔隙像素中任意一点，以该点为球心不断增大球体半径向四周延伸，直至球表面与最近的碎石骨架颗粒接触，所形成的区域内所有像素的集合即为最大球，该最大球可以与1个半径小于它的相邻最大球重叠，形成最大球多簇。填料试样三维重构模型中碎石颗粒间的所有孔隙均被最大球多簇填满，将最大球多簇中半径最大的球体称为该多簇的“祖先”，若1 个最大球多簇中同时拥有2个祖先，则这个公共的最大球所在位置即为喉道，如图5所示[23]。在最大球算法的基础上，以“球”表示孔隙，“棍”表示孔隙与孔隙连接的喉道，建立三维重构模型的球棍模型。

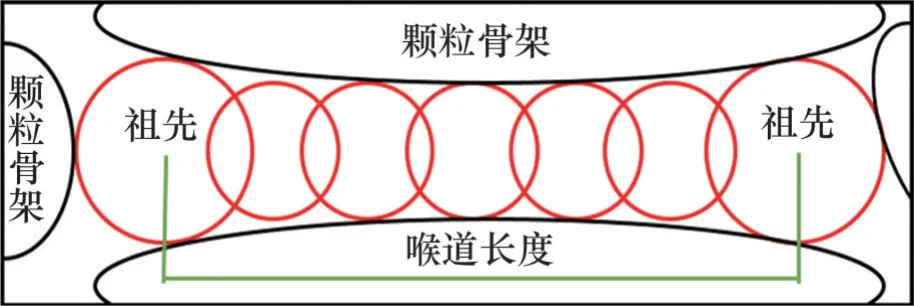
图5 最大球原理示意图[23]Fig. 5 Schematic diagram of the maximum sphere principle[23]

依据上述最大球算法建立的不同G/S粗粒土填料试样的球棍模型如图6所示。根据球的体积可以判断孔隙体积，根据棍的长度及半径可以判断孔隙间的连通性[31-32]。通过孔隙的半径和2个相邻孔隙间狭长通道(即“喉道”)的长度及半径等指标定量描述孔隙尺寸及连通性特征。其中，孔隙半径为孔隙等效半径，即与孔隙体积相等球体的半径；喉道半径为可放置于喉道结构中最大球体的半径；喉道长度为球棍模型中最大球多簇“祖先”间的距离，其具体数值可通过Avizo软件获得；孔喉比为填料试样内部局部范围内孔隙半径与其相连接的所有喉道半径的平均值之比[23]；配位数指与单个孔隙相连接的喉道数目。

3 级配对孔隙连通性的影响

3.1 三维孔隙的半径及其分布

基于XCT 扫描及三维重构的压实后填料试样内部孔隙三维模型，获取不同级配填料试样内部孔隙半径，其半径统计如图7 所示。由图7 可知：不同G/S的填料试样其内部孔隙半径的统计特征差异不大。此外，为评价不同G/S的填料试样其内部孔隙半径的离散性，还计算了其平均值、标准差、极差和变异系数等指标，见表2。从表2 可见：G/S=1.0 的填料试样平均孔隙半径最小；随着G/S增大，平均孔隙半径也增大。这与于群丁[30]的研究结论相一致，即悬浮密实型颗粒堆积结构(G/S=1.0 的填料试样)的填料振动压实后形成的孔隙数量多，但以微孔隙为主且孔隙形状较为规则。G/S=1.8 的填料振动压实后内部小孔隙、微孔隙减少，而G/S=2.5的填料振动压实后内部中孔隙、大孔隙明显增加。随着G/S增大，粗粒土填料内部孔隙半径的离散程度增大，其原因可能是填料内部的中孔隙和大孔隙数量随G/S增大而增多。

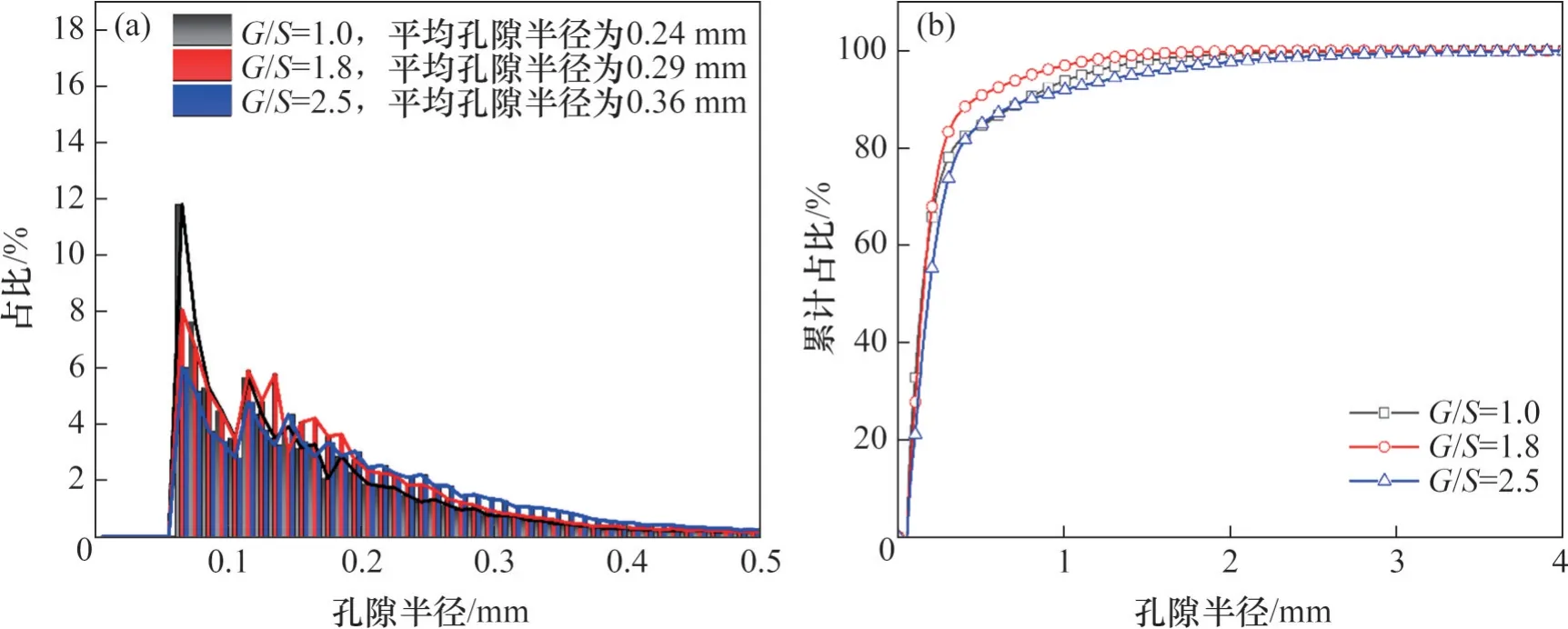
图7 不同G/S的填料试样振动压实后内部孔隙半径占比图Fig. 7 Histograms and cumulative proportion curves of radius values of internal air voids of unbound aggregate specimens with different G/S subjected to vibratory compaction

3.2 三维喉道特征及其分布

图8 和图9 所示分别为不同G/S的填料试样内部喉道长度与半径的统计图。从图8 和图9 可见：不同G/S的填料试样振动压实后，内部喉道半径与喉道长度均存在较大差异；G/S=1.0 的填料试样内部的平均喉道半径与长度最小，喉道长度呈多峰分布而喉道半径呈单峰分布，表明其原因可能是孔隙连通通道较为细小。G/S=1.0 的填料试样内部孔隙小且孤立，换言之，其三维孔隙结构的球棍模型中“球”与“棍”的差异较小；G/S=1.8 的填料试样内部的喉道长度呈单峰分布而喉道半径呈多峰分布；相较于G/S=1.0的填料试样，其喉道长度累计占比曲线整体向右移动，而其喉道半径累计占比曲线则整体向左移动，这说明粗颗粒之间形成了较好的骨架且骨架间的喉道较长，但试样内部的细颗粒较好地填充了粗颗粒骨架之间的孔隙，进而将其通道阻断，使喉道长度减小，并出现多个峰值；G/S=2.5 的填料试样内部的喉道长度与半径累计占比曲线明显整体右移，形成的孔隙连通通道粗而长。

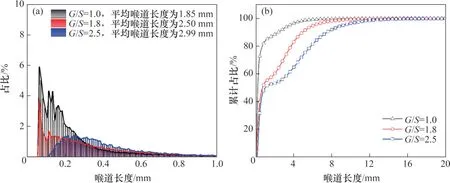
图8 不同G/S的填料试样振动压实后内部孔隙喉道长度分布曲线Fig. 8 Histograms and cumulative proportion curves of throat path lengths connecting internal air voids of unbound aggregate specimens with different G/S subjected to vibratory compaction

图9 不同G/S的填料试样振动压实后内部孔隙喉道半径分布曲线Fig. 9 Histograms and cumulative proportion curves of throat path radius connecting internal air voids of unbound aggregate specimens with different G/S subjected to vibratory compaction

3.3 孔隙结构的均质性特征

本文采用“孔喉比”指标定量评价粗粒土填料内部三维孔隙结构的均质性。局部范围内孔隙与喉道之间的差别随孔喉比增大而增大，即孔隙结构在细观尺度上的变化越剧烈，且三维孔隙结构的均质性越差。图10 所示为不同G/S的填料试样振动压实后的孔喉比占比计算结果。由图10 可见：3种不同类型的颗粒堆积结构所对应的孔喉比多集中于1～2，且占比整体差异较小；与G/S=1.0和G/S=1.8 的填料试样相比，G/S=2.5 的填料试样其孔喉比介于1～2的占比更少，而较大的孔喉比的占比更多，说明G/S=2.5的填料其局部孔隙结构变化较剧烈；相较于G/S=1.0 的填料试样，G/S=1.8填料试样的孔喉比在2～3 的占比出现小幅度增大，说明G/S=1.0的填料试样其内部孔隙结构发育更加规则，这与试样孔隙本身形状较规则相一致[30]。

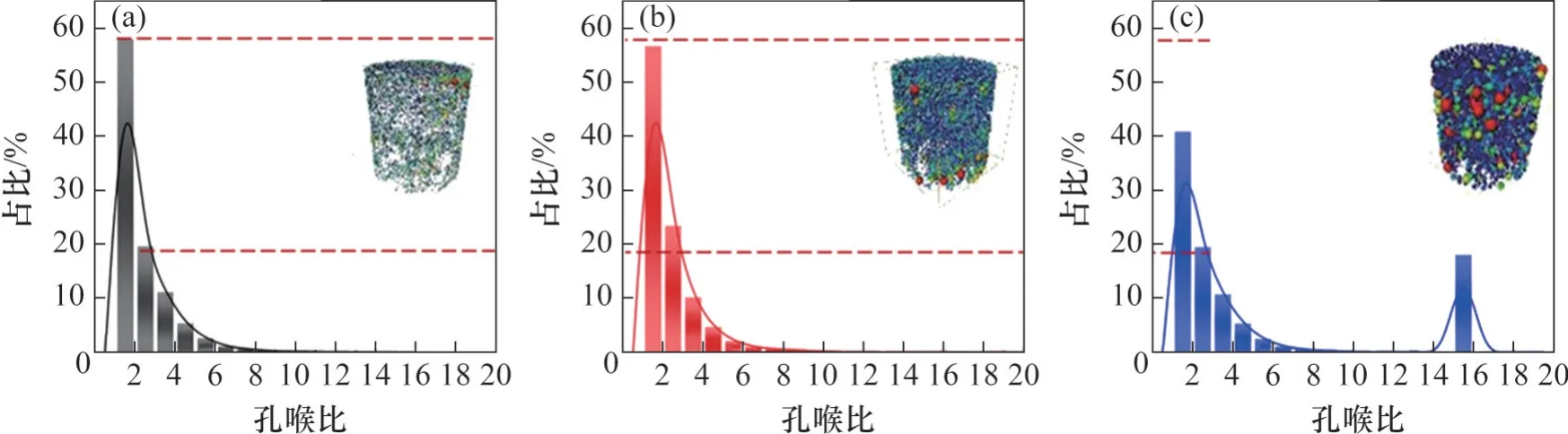
图10 不同G/S的填料试样振动压实后的孔喉比指标值占比分布结果Fig. 10 Histograms proportion curves of the radius ratio between pores and connecting throat paths of unbound aggregate specimens with different G/S subjected to vibratory compaction

3.4 内部孔隙的整体连通性

本文采用平均配位数定量评价粗粒土填料内部孔隙的整体连通性，其值越大说明填料内部孔隙连通性越好。图11 所示为不同G/S的填料试样振动压实后其平均配位数的分布直方图。由图11可见：平均配位数主要集中于0～1，大多为封闭型孔隙，且随着G/S增大，该取值范围内的占比逐渐减小，内部孔隙的平均配位数逐渐增大，试样内部连通型的孔隙逐渐增多，这表明G/S越大，粗粒土填料内部孔隙在细观尺度上的连通性越好。其原因可能是随着G/S增大，填料的颗粒堆积结构从悬浮密实型(其G/S=1.0)逐渐过渡到骨架密实型(其G/S=1.8)，进而过渡至骨架孔隙型(其G/S=2.5)，在此过程中，孔隙结构中的喉道形态由细长型渐变为粗短型，直至试样内部形成粗而长的连通通道。

图11 不同G/S的填料试样振动压实后的孔隙配位数分布直方图Fig. 11 Histogram of pore coordination number distribution of unbound aggregate specimens with different G/S subjected to vibratory compaction

4 基于三维孔隙结构的压实试样渗流模拟

绝对渗透率作为衡量渗透性能的固有物理参数，对于研究流体在路基基床中的渗流过程具有重要意义。绝对渗透率反映岩石孔隙中仅有一种不与岩石颗粒起任何物理、化学反应的单相流体通过的能力。对于不可压缩的流体，可用达西定律求解绝对渗透率，如式(1)所示。

式中：Q为单位时间内流过试样的流量，cm3/s；K为绝对渗透率，cm2；k=KD；Δp为驱替压差，Pa；D为试样的横截面积，cm2；μ为流体的动力黏度，Pa·s；L为流体流过试样的长度，cm。

利用Avizo 软件中的Absolute Permeability Experiment Simulation 模块模拟计算不同G/S的粗粒土填料试样的绝对渗透率。本次绝对渗透率模拟所用流体为纯水，20 ℃时水的动力黏度为1.005×10-3Pa·s，默认模拟输入压力为1.5 MPa，输出气压为标准大气压力(约0.1 MPa)。由XCT 扫描结果可知，不同G/S的填料试样内部孔隙结构沿高度方向呈明显的不均匀性。为更精确地模拟其渗透性能，针对G/S为1.0、1.8 和2.5 的填料试样，在其三维模型中心选取边长为50 mm 的正方体单元，开展沿填料试样高度方向的三维渗流模拟，模拟结果见表3，其中，渗透系数可由下式计算得到：

表3 不同G/S的级配碎石填料试样振动压实后的渗透系数模拟结果对比Table 3 Comparison of simulated coefficient of permeability of unbound aggregate specimens with different G/S after vibration compaction tests

式中：κ为渗透系数，cm/s；K为绝对渗透系数，cm2；υ为流体的运动黏度，cm2/s，即流体的动力黏度与密度的比值；g为重力加速度(取10 m/s2)。不同G/S的级配碎石填料试样振动压实后的渗透系数模拟结果对比，如表3所示[33]。

由表3可知：随着G/S增大，填料试样内部孔隙的平均配位数与渗透系数模拟值均呈现出增大趋势。平均配位数主要取决于连通孔隙，相互孤立且不连通的孔隙对粗粒土填料增加的平均配位数贡献较小，对提高试样渗透性能的贡献也较小，因此，采用单一的孔隙率衡量级配碎石填料渗透性能仍存在缺陷，无法体现孔隙连通度对渗透性能的影响。

利用彩色流线(illuminated streamlines)将上述在渗流模拟过程中所生成的速度场可视化，进而得到不同G/S的粗粒土填料内部渗流的速度场流线图，如图12 所示，其中流线的颜色越接近红色表示流速越大，越接近紫色表示流速越小。由图12可知：G/S为1.0 的填料内部渗流速度较小，这主要是由于G/S较小时的填料内部连通性较好的孔隙较少，缺少较好的渗流通道；而G/S为1.8 时，填料中大孔隙增多，连通孔隙通道变为粗短型，渗流通道变宽，因此，其内部渗流流线图的颜色逐渐趋于红色，表明渗流速度明显加快；随着G/S增大，流线逐渐变密变粗，相比G/S为1.0和1.8的填料内部渗流流线图，G/S为2.5 时，填料渗流模拟中红色流线的数量及长度明显增加，表明其渗流速度较大，进一步证明了粗而长的连通孔隙是主要的渗流通道，且对粗粒土填料的渗透性起着至关重要的作用。

图12 不同G/S的填料试样振动压实后的三维渗流模拟速度流线图Fig.12 Simulated velocity streamline contour plots of seepage flows within unbound aggregate specimens with different G/S

5 三维孔隙连通性及渗透率与级配参数的相关性

为进一步量化分析粗粒土填料的级配(石砂质量比G/S)对细观孔隙连通性和宏观渗透系数的影响效应以及三维孔隙连通性指标与渗透系数之间的关联性，采用Pearson 相关系数(r)来量化三维孔隙连通性指标及渗透率与G/S的相关性，其值介于-1～1 之间。当2 个变量的线性关系增强时，相关系数趋于1 或-1；当相关系数大于0 时，2 个变量之间呈正相关；当相关系数小于0 时，2 个变量之间呈负相关。不同参数之间的统计相关性热力图如图13所示，其中热力图中的数值即为Pearson相关系数。由图13可见：级配参数G/S与孔隙半径、喉道长度和喉道半径等之间的Pearson 相关系数均大于0.95，其与绝对渗透系数之间的Pearson 相关系数也达到0.88，然而，其与配位数之间的Pearson相关系数较低(仅为-0.13)，表明级配参数G/S可较好地控制基床粗粒土填料内部的三维孔隙连通性及渗透系数，即可通过优化G/S参数来优化基床粗粒土填料振动压实后的渗透性能。此外，在表征三维孔隙连通性的指标中，除配位数以外的其他指标与绝对渗透系数之间的Pearson 相关系数均大于0.85，尤其是孔喉比与绝对渗透系数之间的Pearson相关系数接近于1，表明孔喉比可更好地表征和量化基床填料振动压实后的渗透性能。相关性统计分析结果还进一步表明，级配参数G/S主要通过影响孔隙半径、喉道长度和喉道半径，进而影响孔喉比及试样内部的渗流速度。针对不同G/S的粗粒土填料，综合对比分析其室内平板振动压实试验获得的干密度、孔隙结构特征量化结果以及三维渗流模拟结果可知，在保证压实度较大的情况下，可选用G/S较大(即粗颗粒含量较高)的级配设计方案，以确保振动压实后的基床粗粒土填料内部存在连通性较好的孔隙结构及渗流通道。

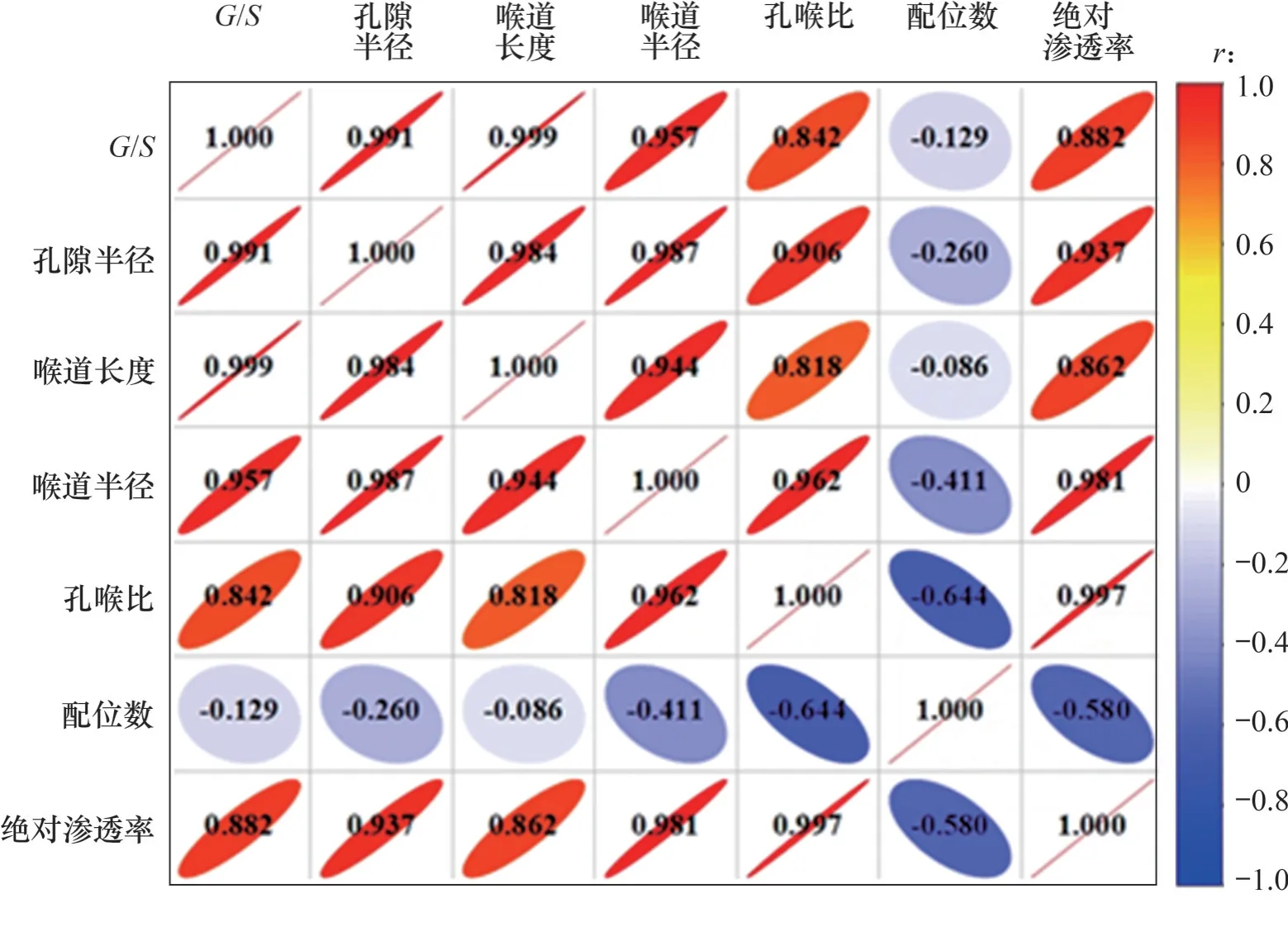
图13 基床粗粒土填料的宏观级配参数G/S与细观孔隙连通性指标之间的统计相关性热力图Fig.13 Thermodynamic diagram showing statistical correlations among macroscopic gradation parameters G/S and mesoscale parameters of internal air void connectivity of unbound aggregate materials

6 结论

1) 级配参数(石砂质量比G/S)影响填料内部的孔隙及喉道特征。随着G/S增大，中孔隙和大孔隙数量增多，平均孔隙半径增大，孔隙半径的离散程度增大，喉道长度及半径均增大，即孔隙间的连接通道越粗越长，孔隙的连通性越好。

2) 填料内部的孔隙半径、喉道长度及喉道半径等表征了孔隙的连通性；3 种不同G/S所对应的孔喉比多集中于1～2，孔隙平均配位数主要集中于0～1。随着G/S增大，孔喉比越大，孔隙结构在细观尺度上的变化越剧烈，孔隙的平均配位数增大，喉道形态由细长型渐变为粗短型，孔隙之间的连通性增大。

3) 级配参数G/S和三维孔隙结构对粗粒土填料的渗透性起着至关重要的作用。随着G/S增大，孔喉比增大(连通性变好)，粗而长的连通孔隙逐渐成为主要的渗流通道，渗流速度增加，渗透性变好。故在保证压实度较大的情况下，可选用G/S较大的级配设计方案，以确保振动压实后的填料仍具有较优的孔隙连通性及渗流通道，保持路基基床良好的施工后渗透性能。

4) 级配参数G/S主要影响孔隙半径、喉道长度和喉道半径，进而影响孔喉比及渗流速度。传统的孔隙率因其无法表征孔隙的连通性而不能准确表征基床粗粒土填料的渗透性能，可采用孔喉比来表征细观孔隙的连通性进而更准确地衡量填料的渗透性能。