喷墨打印量子点薄膜：墨水溶剂的选择策略

欧家琦， 彭曾一， 王俊杰， 李丹阳， 宋家宁， 彭俊彪

（华南理工大学 发光材料与器件国家重点实验室， 广东 广州 510641）

1 Introduction

Inkjet printing（IJP） of quantum dots（QDs）droplets is gaining popularity due to its promising potential in displays[1]. QDs have emerged as an alternative to the traditional non-emissive color filters in LCDs or the self-emissive functional layers in OLEDs due to their striking properties including narrow-spectrum luminescence, high quantum yield and solution processability[2-7]. Inorganic colloidal QDs are the most commonly used type of QDs in inkjet printing QLEDs, including CdSe, InP, and CdTe[8-9].Polymer-based QDs and small-molecule-based QDs are also frequently used in this field, known for their high stability and high efficiency, respectively[10-11].Poly（9,9-dioctylfluorene-co-bis-N,N-（4-butylphenyl）-bis-N,N-phenyl-1,4-phenylenediamine）（PFB）is a typical example of the former, while 4,4′-bis（Ncarbazolyl）-1,1′-biphenyl （CBP） is a typical example of the latter. IJP boasts several operational advantages over spin-coating and vacuum-evaporation,such as precise patterning, large-area film producibility and low material wastage[3,12-14]. To ensure uniform light emission as well as efficient carrier transportation in high-quality optoelectronic devices, uniform thickness and smooth surface are required for each functional layer, rather than the typical unideal coffee-ring or bulge morphology[15]. The solvent evaporation and solute deposition of sessile QDs droplets on substrates determine the film profile[16-18]. There are a plethora of factors that can influence the dynamics of droplet drying[19]. Specifically, we are interested in how the solvent rheological properties can alter the deposited film profile and eager to find out the more efficient means to tailor it, which is the motivation for this research.

Micro-droplet drying is a very complex process,and its simplification is therefore crucial for efficiency optimization. It can be summarized that vapor,liquid and solid phases may influence the final film morphology of a picoliter QDs droplet by changing the interfacial mass transfer fluxes and contact line motions[20], which in turn affects the internal flow pattern of the droplet, as presented in Fig. S1. Specifically, solvent engineering has been applied in a wide range of material systems as it can significantly adjust evaporation kinetics[16-18,20-22]. Essentially, it takes advantage of the differences in rheological properties of solution between different regions within a droplet to control the internal flow behavior during drying,thus altering the solute distribution to form the desired films[20,23]. The widespread use of solvent modulation is based on its operational ease and remarkable impacts, as a small amount of another solvent could cause dramatic effects[24-26]. However, the droplet drying process is extremely complex due to a variety of physical mechanisms and a number of factors involved, making solvent modulation simple to carry out but difficult for precise regulation. In most cases, boiling point（Tbp）, surface tension（γ） and viscosity（η） are the three key rheological parameters that have the most significant influence on the droplet drying process[18], and clarifying the specific roles and contribution weights of the three parameters to film formation is of vital importance for the efficient formulation of QDs inks, the preparation of thin films with uniform thickness and flat surface, and the processing of high-performance quantum dot light-emitting diodes（QLEDs）[27]. However, the direct connections between film quality and these parameters still need to be studied.

Besides the fruitful studies on unitary-solvent inks, several pairs of binary solvents were reported to produce uniform films for QLEDs in recent years,hugely boosting the eternal quantum efficiency[28-33].They discovered that preventing interlayer erosion[30-31,33], balancing capillary outward flow and Marangoni flow[28,32,34]and controlling the three-phase line motions[29]are the keys to affect the film morphology and thus the efficiency of the device. However, ink engineering, the crucial process to realize the large-area and low-cost fabrication of cuttingedge devices, still largely depended on recipes developed by manual trial and error based on semi-empirical theories in most of the previous research. Specifically, multiple effecting factors and corresponding film-forming mechanisms were studied and presented from a qualitative point of view, which brought confusion and difficulties to efficient ink tailoring.Therefore, clarifying the functions of each solvent component and the order of priority of diverse factors makes sense and matters a lot.

In this work, we tried to bridge the gap between the rheological properties of solvents and the film profiles of inkjet-printed colloidal QDs droplets using post-mortem film analysis,in-situobservation of the drying process and machine learning. Temporal observations of the drying process and theoretical calculations were main analyzing tools, while machine learning models based on data simulation were involved to help support conclusions to reduce labor and time costs. By integrating experiments and modeling for cross-check and mutual proof, we correlated the rheological properties of solvents and final film profiles of inkjet-printed QDs drops, expecting to offer a more efficient insight into the selection of the solvent components to mitigate coffee rings or bulges.

2 Experiment

2.1 Materials

The red QDs were purchased from Shenzhen Planck Innovation Technology Co., Ltd., China. n-Octane and n-Hexadecane with purity better than 99% were purchased from Sigma-Aldrich Inc., Germany. n-Nonane, n-Decane, n-Undecane, n-Dodecane, n-Tridecane, n-Tetradecane, n-Pentadecane, bicyclohexane, methyl dodecanoate, methyl tridecanoate, amyl hexanoate, butyl hexanoate, methyl decanoate, chlorobenzene and decalin were purchased from Aladdin Ltd., China. Heptylcyclohexane, nonylcyclohexane and hexyl hexanoate were purchased from Macklin Inc., China. Octylcyclohexane was purchased from Tokyo Chemical Industry Co., Ltd., Japan. All the solvents were filtered through a 45-μm polyethersulfone syringe filter for organic solution samples before used.

2.2 QDs Ink Preparation

QDs powder was dissolved with an appropriate amount of the modulated solvent to make a concentration of 30 mg/mL. The fresh QDs ink was shaken evenly for uniform dispersion and filtered through a 0.45-μm polytetrafluoroethylene filter to remove impurities. The QDs ink was then loaded into a cartridge for printing. Therefore, the QDs ink consists of a volatile liquid or a mixture of two volatile liquid and QDs with an average size of （9.377 ± 1.544）nm（Fig.S2）.

2.3 QDs Film Preparation

The QDs ink droplets with various formulations were inkjet-printed at ambient temperature by a piezoelectric printer（JetLab II） with a 20-μm nozzle from MicroFab Technologies, Inc., USA. The voltage waveform and negative pressure of the printer were adjusted to generate a string of vertical drops.The printer parameters and calibrate position were set to fix the printing patterns on the perfluoropolyethers（PFPE） substrate with surface energy of 45-50 mN/m. After printing, the samples were dried out at room temperature and were taken off from the platform for further characterization.

2.4 Characterizations

The shape and size distribution of QDs were determined from a transmission electron microscopy（TEM, JEM-1400 Plus） from JEOL Ltd., Japan.The luminescence spectrum was recorded by a spectroscopy（QE Pro） from Biaoqi Electronics Technology Co., Ltd., China. The viscosity of the QDs inks or pure solvents was obtained by a rotational viscometer（LVDV-I+） from Brookfield AMETEK Inc., USA,while the surface tension was measured by an optical tensiometer （Theta Lite Model TL 100） with its corresponding software OneAttension from Biolin Scientific, Sweden. The post-mortem film profiles of QDs films were observed by a 3D laser confocal scanning microscope（LEXT OLS5000） from Olympus Optical Co. Ltd., Japan. The normal and fluorescent images of the QDs films were captured by a polarized light microscope（Axiolab 5 with Axiocam 105 Color Microscope Camera） from Carl Zeiss Microscopy GmbH, Germany in normal mode and fluorescent light mode respectively. All the measurements were carried out at temperature about 25 ℃ and humidity about 55%.

2.5 Profile Datasets

Fig.1 shows the quantitative parameters measured from a film profile captured by a 3D laser confocal scanning microscope. In Fig.1（a）, central height（H） refers to the average height of the area with a length equal to 10% of diameter（D） in the middle of the film. As mentioned above, the typical unideal film morphology may be coffee rings or bulges. The coffee ring effect describes an unideal profile of the film where most of the solutes migrate to the rim and accumulate there, resulting in a typical concave volcano-like profile[21,35]. On the contrary, bulges result from the accumulation of QDs in the middle, which causes a convex mountain-like profile[16,35]. Therefore, surface curvatureAshown in Fig. 1（b）, which was obtained from a quadratic functionf（x） =Ax2+Bx+C, was defined to characterize the convexity of the film surface in this work. Four sample groups of film surface data, which implied concave（b1）, flatununiform（b2）, flat-uniform（b3） and convex（b4）film respectively, were fitted into the function for suitability check, whose results are presented in Tab. S1. The b2, b3 and b4 groups displayed perfect fitting with the coefficient of determinationR2=1.000 while the b1 group performed slightly badly withR2= 0.498, which might be attributed to a mismatch between the smooth fitted curve and the original steep inner side of the ring structure. However,these results proved sufficient feasibility for quadratic function in surface profile characterization, whereA＞4E-6 indicates concave whileA＜-4E-6 indicates convex and the range 4E-6≥A≥-4E-6 indicates flat surface with a spin-coated film as the standard one（Fig.S3）.

For the unitary-solvent ink system, boiling point, surface tension and viscosity of pure solvent were used as input variables to build a Random Forest Model for predicting the surface curvature of the film profile. For a binary-solvent ink system, the difference between boiling points（ΔTbp）, surface tension（Δγ） and viscosity（Δη） of the minor solvent（30% vol） and the major solvent（70% vol） were used as input variables defined as equation （1）, （2）and （3） respectively:

2.6 Model Construction

Furthermore, four datasets consisting respectively of 120 pairs for unitary-solvent system（Tab.S2）, 56 pairs for binary-solvent system using decalin as the major solvent（Tab. S3）, 120 pairs for binarysolvent system using bicyclohexane as the major solvent（Tab. S4） and 64 pairs for binary-solvent system using octylcyclohexane as the major solvent（Tab.S5） were constructed.

Firstly, we constructed Random Forest Models to calculate feature importance[36-37]. The pseudocode for this process is presented below:

（1） Initialize an empty dictionary to store feature importance scores.

（2） For each tree in the forest:

a. Traverse the tree and calculate the total decrease in node impurity（weighted by the probability of reaching that node） for each feature.

b. Add the feature importance scores to the dictionary.

（3） Normalize the feature importance scores by dividing them by the sum of all feature importance scores.

（4） Return the normalized feature importance scores.

Secondly, we used the Random Forest Models to make predictions. The pseudocode for this process is presented below[38]:

（1） For each tree in the forest:

a. Traverse the tree and predict the outcome for the test data.

b. Store the predicted outcome.

（2） Calculate the mode of the predicted outcomes across all trees.

（3） Return the mode as the final prediction.

In our work, all the datasets were then independently divided into training and test sets at a ratio of 8-2 and used for the construction and evaluation of the prediction model.

3 Results and Discussion

The rheological properties of the prepared solvents were divided into four groups, as shown in Tab. S6, S7, S8 and S9, corresponding respectively to a unitary-solvent system and three binary-solvent systems with decalin（DCL）, bicyclohexane（BCH）and octylcyclohexane（OCH） as the major solvent respectively. No nozzle clogging was observed during all the printing processes, which indicated that the boiling points of the chosen solvents were high enough to ensure a stable droplet formation over a long time period. Fig. S4, S5, S6 and S7 show the corresponding deposited film profiles from which all the data were measured according to the measurements depicted in Fig.1. Information about diameterD, and central heightHcould be found in Fig. S8 and S9 for unitary-solvent ink system and binary-solvent ink systems respectively.

All the unitary solvents were divided into four group based on their chemical structure, corresponding to cyclohexane-X（sample #1-sample #3）, cyclohexane-alkane（sample #4-sample #6）, alkane（sample #7-sample #10） and ester（sample #11-sample #15）, according to the tags noted in Tab.S6. Since solvents of the same group have similar structures and properties, one solvent was chosen from each group: bicyclohexane, n-octyl cyclohexane, n-hexadecane, and methyl dodecanoate. The morphology and particle size distribution of the nanoparticles were measured by TEM. As shown in Fig. S10（a）,S10（b）, S10（c）, S10（d）, after being dissolved in the above four solvents, the size of the quantum dots did not change significantly compared to that in n-octane（Da= （9.377 ± 1.544） nm）. It should be noted that after being dissolved in methyl dodecanoate,the particle size distribution range of the quantum dots was slightly wider（Fig. S10（e））, which is because quantum dots tend to aggregate slightly in ester solvents with weak polarity（Tab. S6）, but still within a good range of solubility. These histograms proof good interaction between quantum dots and the solvents. Fig.2（a）-（c） show the relationship of surface curvatureAwithTbp,γ, andηof pure solvent in the unitary-solvent system respectively. It was found thatAdecreased asTbp,γ, andηincreased in every single group. However, despite different chemical structures,Adecreased as theTbpincreased as a whole, whileAdid not exhibit such obvious correlations withγorη（Fig. 2（b） and （c））. Therefore,Tbpwas deluded to be the key parameter decidingAof the deposited film profile.

Fig.2 Experimental data and a drying diagram of unitary-solvent system. Relationships between A and Tbp（a）， γ（b）， and η（c）of pure solvent. （d）Sticking time tstick and sliding time tslide of the three ink droplets during drying. （e）Schematic diagram of the three stages of drying a QDs ink droplet. Cɑ refers to capillary flow inside the droplet.

Generally,Tbpof solvent controls the evaporation rate, whileγdecides wetting andηdetermines the internal friction of solvent[21]. The evaporation rate relates closely to the speed of capillary compensation flow inside the droplet[20]. The faster the evaporation, the faster the liquid flows[16]. Besides,wetting affects liquid flow with adhesive force between droplet and substrate[39]. The lower the adhesive force, the faster the liquid flows. Moreover, internal friction suppresses flowing[40]. The lower the friction, the faster the liquid flows. Therefore, lowerTbp,higherγand lowerηcan promote flowing. Fig.S11 shows the temporal evolution for ink droplets with unitary solvents of （a） bicyclohexane（sample #2）, （b） n-tetradecane （sample #8） and （c） octylcyclohexane（sample #5） respectively taken by an optical microscope. Two changing processes of threephase contact line, sticking and sliding, were depicted in Fig. S11, whose durations were then denoted correspondingly aststickandtslidepresented in Fig.2（d）. Previous work has reported that the descending of droplet surface during the initial period of drying is attributed to a large amount of solvent dismissing into the air[20,41-43]. Therefore, with the correspondingTbpof the three solvents increasing, thetsticklengthened. Interestingly, the second stage was different from what had been observed before[18], the droplet neither dried out with a pinned rim nor slid on the substrate. Instead, the rims of the three droplets all slid right on the deposited QDs film and the droplet ultimately dried out in the middle of the film. This scenario may be attributed to the relatively low surface energy of PFPE substrate（45-50 mN/m）, which enabled easier depinning for the rim. Several rules for substrate selection were listed before[12,28,32], including solvent orthogonality and good wettability emphasized the most, based on which an ultra-thin PFPE was chosen as the interfacial layer between the transporting layer and the QDs emitting layer.Firstly, PFPE lacks solubility in organic solvents,preventing interfacial erosion between different functional layers. Secondly, despite low surface energy compared to the usual transporting layer, PFPE can provide sufficient wettability for the solvents selected in this work because a substrate can be fully wetted once the surface tension of the liquid is lower than that of the substrate[23,44-45]. Besides, this smaller gap between the two surface tensions enables weaker pinning of the three-phase contact line, thus accelerating in the depinning process. Herein, withγandηrising in turn, their influence on the flow ability of liquid canceled out, resulting in a similartslidefor different solvents. Specifically, Fig. 2（d） shows that thetstickis longer than thetside.During thetstick, the dissipative force of the solvent molecule into the ambient air is quite violent and drags the solvent to the rim, thus hugely affecting the locations of solutes at the beginning. However, in the bulk liquid phase,viscosity has a small impact because the droplet is not flowing at this moment. Additionally, due to the violent evaporation at the rim, the solvent displays weaker wetting on the substrate. As time passes,this force gradually reduces, but the amount of solvent in the droplet is far less than at the beginning,which is unable to move the solutes despite constriction to the middle of the film duringtside.

Herein, three stages of evaporation of an ink droplet on a PFPE substrate were depicted in Fig.2（e）. In stage Ⅰ, the rim of the droplet pins, and the height of the liquid surface drops because of the capillary compensation flow towards to rims inside the droplet during evaporation. This stage, who lasts for a longer time, is mainly controlled by the boiling point and also affected by the surface tension. The lower theTbp, the higher the evaporation rate, and further the shorter thetstick; with the sameTbp, the lower theγ, the smaller the contact angle, and further the shorter thetstick. In stage Ⅱ, the droplet overcomes pinning. At this point, the droplet has to overcome the obstruction on the rim,i.e., the realtime deposited QDs. Therefore, a solvent with lower viscosity with stronger flow ability is easier to break free from pinning. In stage Ⅲ, the three-phase contact line of the droplet slides on the deposited QDs film until the droplet dries out. To maintain the spherical shape, the rim of the ink droplet slides inward driven by surface tension[18], whereas viscosity controls the ability of a liquid to flow[28,46]. Herein,this stage is controlled by surface tension and viscosity, the higher theγor the lower theη, the shorter thetslide. Considering the longertstickcompared totslide,Tbpwas considered the most important parameter to determine the ultimate deposited profile of QDs film in the unitary-solvent system, followed byγandηin sequence. Additionally, within all the inks prepared, QDs ink with octylcyclohexane（Tbp=259 ℃,γ= 31.6 mN/m,η= 3.11 cP） as the unitary solvent could be used to print flat film.

Fig. 3 shows the relationships ofAwith ΔTbp,Δγ, and Δηof pure solvents, respectively, in binarysolvent systems. Generally,Adecreased as theΔTbp,i.e., theTbp*, increased（Fig.3（a））. For DCL-based group, concave film appeared mostly when ΔTbp≤44.10 ℃ while convex film appeared when ΔTbp≥58.00 ℃ without a flat film achieved. For BCHbased group, concave film appeared when ΔTbp≤15.00 ℃ while convex film appeared when ΔTbp≥29.30 ℃, and a flat film was achieved when ΔTbp=20.00 ℃. For OCH-based group, flat films were formed when ΔTbp= -20.00 ℃ or ΔTbp= -5.00 ℃,and convex film appeared mostly when ΔTbp≥ 5.50 ℃without a concave film recorded. On the contrary,Adid not exhibit obvious correlations with Δγor Δη（Fig. 3（c） and （d））. Boltzmann sigmoidal fitting was further adopted to evaluate the correlations ofAwith ΔTbp, Δγ, and Δηrespectively, whose results are presented in Tab. S10. A strong correlation ofAwith ΔTbpcan be found in each group, although the respective Chi-Sqr value varied as the result of different major solvents used. In comparison, the correlation ofAwithΔηwas weak, because only the BCH-basedA-Δηdataset can be fitted into convergence with a less desirable Chi-Sqr value. Furthermore, the correlation ofAwith Δγwas considered to be the weakest, given none of theA-Δγdatasets could be fitted into convergence. Fig. 3（b） presents theA-ΔTbpBoltzmann sigmoidal fitting lines.On the DCL-based line and BCH-based line, an inflection ΔTbpof 40 ℃ and 1 ℃ existed, respectively, indicating that the film profile started to change from a deep concave towards flat and further convex. However, there was no such an inflection point on OCH-based line because none of binary solvent in this group resulted in concave film in experiments. Preliminarily, it could be deducted from the fitting line three corresponding ideal ΔTbpranges（Tab. 1）, which were 54-56 ℃ for the DCL-based group, 17-21 ℃ for the BCH-based group, and N/A～6 ℃ for the OCH-based group. Combined with the correspondingTbp, the idealranges were 250-252 ℃, 256-260 ℃ and ＜253 ℃. Noticeably, a major solvent with a higherTbpcan tolerate a broader range of boiling point differences for good film formation.

Fig.3 Experimental data and fitting functions of binary-solvent systems. Relationships between A and ΔTbp（a）， Δγ（c）， and Δη（d） of binary solvents. （b）Fitting Boltzmann sigmoidal functions to A-ΔTbp datasets.

Fig.4 Importance of variables on surface curvature A. （a）Unitary-solvent system. （b）Binary-solvent system using decalin as the major solvent. （c）Binary-solvent system using bicyclohexane as the major solvent. （d）Binary-solvent using octylcyclohexane as the major solvent. Inserts： line plots for true values and predicted values of A for the corresponding group by RF models. R2， coefficient of determination on test set data. RMSE， root mean square error on test set data.

It is therefore concluded that the main parameter determiningAis the boiling pointof the minor solvent and its ideal range is between 250-260 ℃. Combing with the results of the unitary-solvent system, it was found that it is the higher-boilingpoint solvent in binary-solvent systems determines the ultimate deposited film morphology, because a unitary solvent with aTbpof around 260 ℃ can also result in flat film. However, it is preferred thatbe higher than that of the major solvent to accelerate the whole drying rate because the small amount. It can stay until the last stage of evaporation despite of smaller amount and thus function to smoothen the ultimate film profile. Furthermore, a low-boiling-point major solvent with good solubility is preferred because it can shorten the overall evaporation duration. WithTbpis less than 260 ℃, flat films are more likely to be realized when the range ofTbp*is between 250-260 ℃.

Tab.1 Properties of three kinds of major solvent and the respective ideal range of boiling point of the minor solvent according to Boltzmann fitting results

Random forest（RF）, a machine learning prediction model, incorporates the importance of input variables for prediction[36]. It yields quantified information about the features and their contribution to the predictionviɑmultiple tree models as shown in Fig.S12. Therefore, RF models were utilized to perform importance analysis and prediction on film profile,i.e.Avalue, in this work. In addition,R2and root mean square error（RMSE） were used as evaluation metrics for the model performance.

Fig. 4 shows the results of the feature importance analysis in each system, where the inserts represent the performance in predictingA. The inserted line plots show that the training and test sets had similar trends. For the unitary-solvent system, the key factor was theTbpof the solvent（Fig. 4（a））, followed byγandηin sequence, which was in good coordination with the experimental result. For the binary-solvent systems, it can be seen that ΔTbptook the first place in the three systems in spite of different major solvents used（Fig. 4（b）, （c）, （d））,whereas the surface tension and viscosity played a less dominating role, indicating the great importance of ΔTbp*. However, the order of Δγand Δηvaried in different systems, which may be attributed to the properties of different major solvents. These RF models accurately predictedAin the unitary-solvent system, the binary-DCL-based system and the binary-BCH-based system withR2values achieving 0.956 7, 0.983 9 and 0.944 2, respectively. ForAin the binary-OCH-based system, anR2value of 0.798 0 was obtained, indicating a less precise prediction which might be attributed to the similar profiles and thus the similarAinputs in this system. In addition, the RMSEs were small in four systems, indicating the acceptable precision.

Furthermore, Fig.5 shows the predictions of different input features onAin the unitary-solvent system（Fig. 5（a）, （b）, （c）） and the binary-solvent systems （Fig. 5（d）, （e）, （f））. In the unitary-solvent system, Fig. 5（a） firstly reveals thatAwas significantly affected byTbp, which could be depicted by the significant differences in stratification at differentTbp. WithTbprising,Agradually changed from positive to negative, implying that the film profile changed from concave to convex. Secondly, the effect ofγonAwas related toTbp（Fig. 5（b））. WhenTbpwas relatively low（190-260 ℃）, highγ（＞ 29 mN/m） corresponded to highA, while lowγcorresponded to lowA; whenTbpwas relatively high （＞260 ℃）, the change ofγperformed ignorable effect onA. Thirdly, the effect ofηonAwas related toTbpandγ（Fig. 5（c））, where the change ofηdisplayed almost no effect onAat any set ofTbpandγ. In binary-solvent systems, Fig. 5（d） reveals that a minor solvent with a higher boiling point promoted the formation of flat films because of the lower evaporation rate during the whole drying process. In addition,with a further increase of the major solvent's boiling point, the combinations that were applicable for a flat film formation increased, benefitting from the general slow evaporation, but this may lead to lengthy drying during which other unideal situations,such as quenching and irregularities, may occur.Fig. 5（e） and Fig. 5（f） show the statistical influence of Δγand ΔηonA, from which we can see that there were no clear effects. These results can be corresponded to the RF importance analysis and were in full agreement with the experimental data and speculative conclusions.

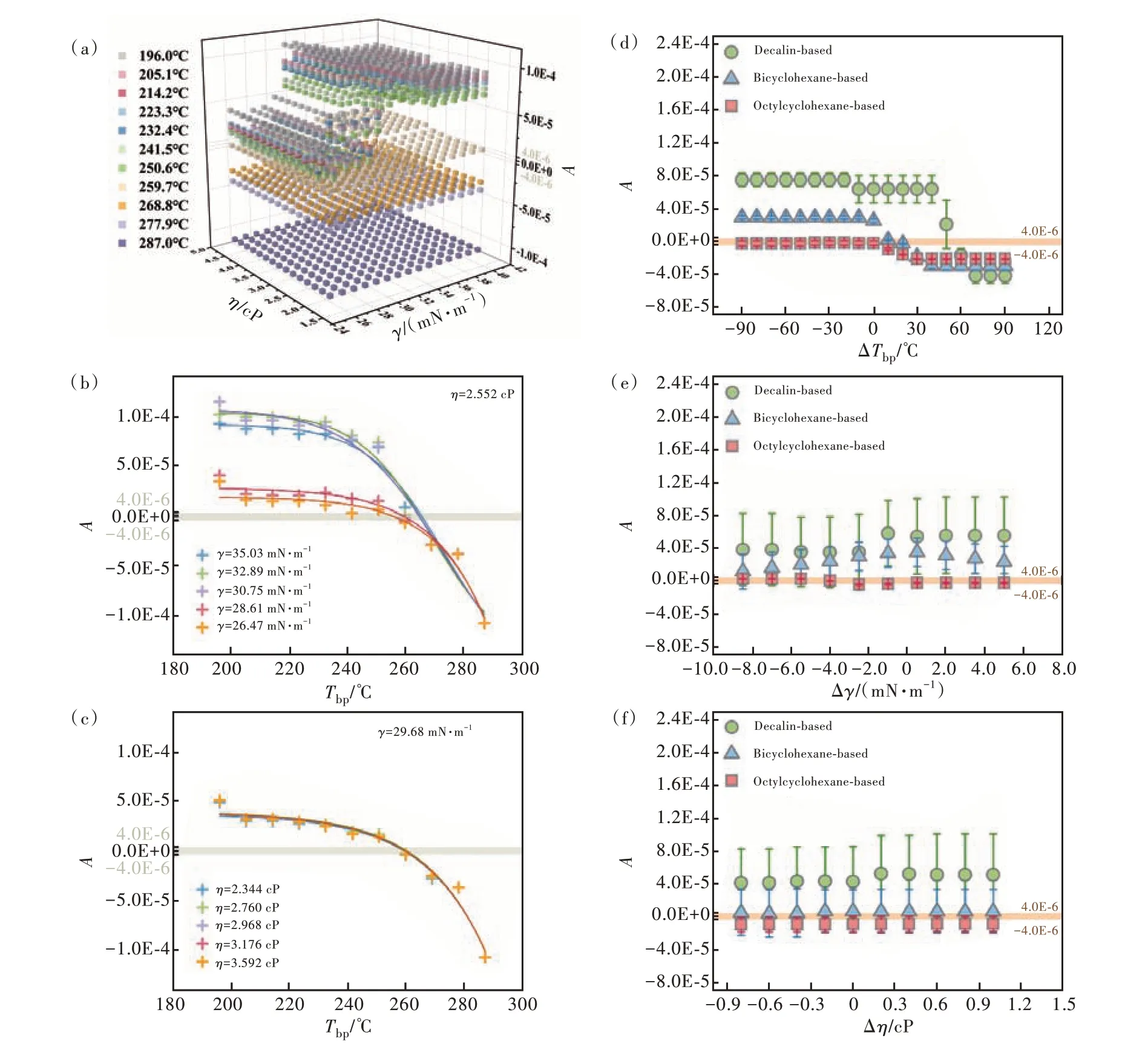
Fig.5 Prediction on surface curvature A by RF models. In the unitary-solvent system. （a）The trend of A with variable Tbp， γ and η of pure solvent. （b）The trend of A with variable Tbp under the same η and different γ. （c）The trend of A with variable Tbp under the same γ and different η. In the binary-solvent systems， the statistic trend of A with variable ΔTbp（d）， Δγ（e）and Δη（f）.

As the result of a longer drying time, the surface irregularities were smoothened. For the unitarysolvent system, solvents withTbpof 250-265 ℃ were preferred. For binary-solvent systems, minor solvents withTbp*of 250-260 ℃ were preferred, while a major solvent with a relatively lower boiling point would be better to offer high evaporation rate during the initial drying stage. In addition, machine learning unveiled the potential of big data analysis in ink engineering, especially considering the complexity and multiple affecting factors. Despite slight errors,such predictions enable effective tweaks of the properties free from labor-intensive trial and error.

4 Conclusion

We first identified the crucial parameter affecting the inkjet-printed QDs film profiles with experimental results as well as machine learning prediction support. The results showed that the boiling point was more important compared with surface tension and viscosity. A boiling point range of 250-265 ℃for the solvent in the unitary-solvent ink system or for the higher-boiling-point solvent in the binary-solvent ink systems can promisingly result in uniform films after drying.

In comparison with previous ink engineering methods, highlighting boiling point avoided complex calculations of the Marangoni number and viscous force, offering a simpler way to find a suitable solvent. In addition, machine learning developed models to conduct prediction and offer guidelines based on the great amount of data, enabling effective tweaks of the properties free from labor-intensive trial and error. Furthermore, it could help consider the multiple parameters related to film morphology including surface energy of substrate and concentration of QDs for finding out more internal clues,which performed as a promising potential trend in this field.

Consequently, this work demonstrated a simpler strategy for tailor-making inks to inkjet-print uniform QDs films and unveiled the potential of machine learning for simplifying ink engineering in the future. Furthermore, more precise fittings of the profiles and more diverse characterizations for the films are needed of further studies to construct more universal models.

Supplementary Information and Response Letter are available for this paper at: http://cjl.lightpublishing.cn/thesisDetails#10.37188/CJL.20230228.