基于多层次灰色综合的常压储罐RBI评价方法研究

赵俊茹 孟凡想 田峻东 张美玲

（东北石油大学机械科学与工程学院）

近年来随着石油化工行业的发展，常压储罐得到广泛应用。 由于其储存介质常具有易燃、易爆、腐蚀性强等特性，一旦泄漏，极易引发安全事故，造成经济损失、人员伤亡等严重后果和重大社会影响［1］。目前，我国石油化工企业对常压储罐管理采用的传统检测方法存在着少检易引发安全事故， 过检造成工作量和成本增加的两大问题。 因此，对常压储罐进行科学评估和有效管理，科学合理地将预防性检测转变为预测性检测尤为重要［2］。

基于风险的检验（Risk-Based Inspection，RBI）本质是对危险事件发生的可能性和后果进行分析和排序。 该技术最早应用于欧美发达国家的承压设备检验与维修中，并取得了较好成效［3，4］。国内首批应用至目前广泛推广已有20余年，RBI风险评估对企业风险管理、装置的长周期运行具有促进作用［5～7］。 但对常压储罐进行RBI风险评估和失效概率计算时，其破坏系数均按照同一比重，没有充分考虑储罐的损伤机理和部位，无法体现不同损伤因子对储罐风险的影响程度，评价结果不够准确。 因此，有必要对传统RBI风险评估方法作适当改进，通过确定各系数在影响储罐失效中所占的恰当比例，实现各损伤因子的权重根据实际情况动态分配，更真实地反映不同储罐所具有的风险［8］。

笔者通过将层次分析法与灰色理论相结合计算常压储罐失效概率， 不仅降低了AHP主观性，避免传统打分造成的风险遮蔽问题，而且通过建立三级评价指标体系，从损伤因子的权重排序中找出影响储罐失效的主要因素。 最后以某常压储罐为例对上述结论进行分析验证，更加证实了该变权思想可动态调整储罐损伤因子的权重，有针对性地计算储罐失效概率结果［9］。

1 常压储罐多层次灰色综合的RBI评价模型研究

多层次灰色综合评价法是将层次分析法和灰色综合评价法结合的一种评价方法。 层次分析法是将定量与定性相结合的多目标决策分析方法，主要用于分析和处理系统化、多层次问题；灰色综合法主要分析和处理涉及纵向序列等问题，充分利用已有的白化信息，减少评判误差［10］，更好地理解系统内部关系和变化趋势。 二者结合可以对复杂系统的各个子系统进行分别评价，同时也可以在子系统评价的基础上对上层系统进行综合评价。

1.1 层次分析法

1.1.1 建立指标体系

据GB/T 30578—2014 《常压储罐基于风险的检验及评价》可知，破坏系数是计算储罐失效概率时起决定性的因素，笔者从此系数入手，根据检测经验和数据分析选取7项影响值较大的因子， 建立常压储罐的三级评价指标体系模型，如图1所示。

1.1.2 构建判断矩阵

根据结构模型，对判断矩阵采用两两比较的方法得出结果， 并采用1～9的数值标度来定义判断矩阵M，各标度的含义见表1。

表1 判断矩阵标度定义

矩阵M的计算式为：

1.1.3 一致性检验

对判断矩阵进行一致性检验时，常用方法有算数平均法、几何平均法、特征值法等。 笔者采用特征值法求出判断矩阵的特征值和特征向量，计算一致性指标CI：

式中 n——判断矩阵阶数；

λmax——最大特征值。

参考表2可得到随机一致性指标RI。

表2 随机一致性指标RI

一致性比例CR的计算式为：

当一致性比例CR＜0.10时，认为判断矩阵符合一致性检验，否则应重新评分，对矩阵M进行修正。

1.1.4 特征向量求权重

将权重向量W右乘权重比矩阵A，则有：

其中，λmax存在且唯一，W的分量皆为正分量，将求得的权重向量作归一化处理。

1.2 多层次灰色综合评价法

1.2.1 确定评价样本矩阵及评价灰类

按照专家评分法，依据评分标准来评价指标层的每个指标， 汇总p位专家对不同因素的打分情况，形成评价样本矩阵D，即：

将评分标准分为“低”、“较低”、“中”、“较高”、“高”5个等级，打分采用9分制，对这5个评价标准分别赋值9、7、5、3、1，具体评分标准参照表3。

表3 评分标准

1.2.2 确定灰类的评价系数

第e个评价灰类的评价系数Xie为：

式中 dik——评价样本矩阵中的元素；

fe——白化权函数。

1.2.3 确定灰色权向量和权矩阵

灰色权向量计算表达式为：

从而得到灰色评价矩阵R为：

1.2.4 综合评价

根据以上数据求得灰色综合评价值B为：

式中 ωM——特征向量即层次权重。

2 常压储罐多层次灰色综合的RBI评价模型的应用

现以某企业的汽油储罐为例， 已知该汽油储罐介质为硫化氢（H2S），具有毒性，操作温度为20 ℃，最低运行温度为3 ℃，储罐填充高度为15.47 m，直径为21.15 m，罐壁设计厚度为140 mm，罐底设计厚度为100 mm，容积为5 000 m3，操作压力1.96 kPa， 罐体材料为Q235， 设计标准为API 650。 储罐的建造符合国家相关规范的要求——建造于较平坦处， 储罐基本数据资料真实明确，检测方法有效。

将多层次灰色综合常压储罐RBI评价模型应用于此实例，评价该储罐罐底的风险等级。

2.1 AHP法确定指标权重

找若干名该领域的专家和技术人员组成评价打分小组， 对储罐破坏系数中准则层的4项因子和指标层的7项因子进行讨论打分，根据表1中的评价标准建立判断矩阵为：

通过MATLAB软件对一级判断矩阵进行计算，得出最大特征值和特征向量为λmax=4.1894，x=［0.8586，0.1046，0.2132，0.4543］。

将特征向量进行归一化处理得出权重向量W=［0.5266 0.0642 0.1307 0.2786］，同理，按以上步骤计算二级判断矩阵， 并通过一致性检验，得到各指标的权重如下：

各要素对破坏系数A的权重排序见表4。

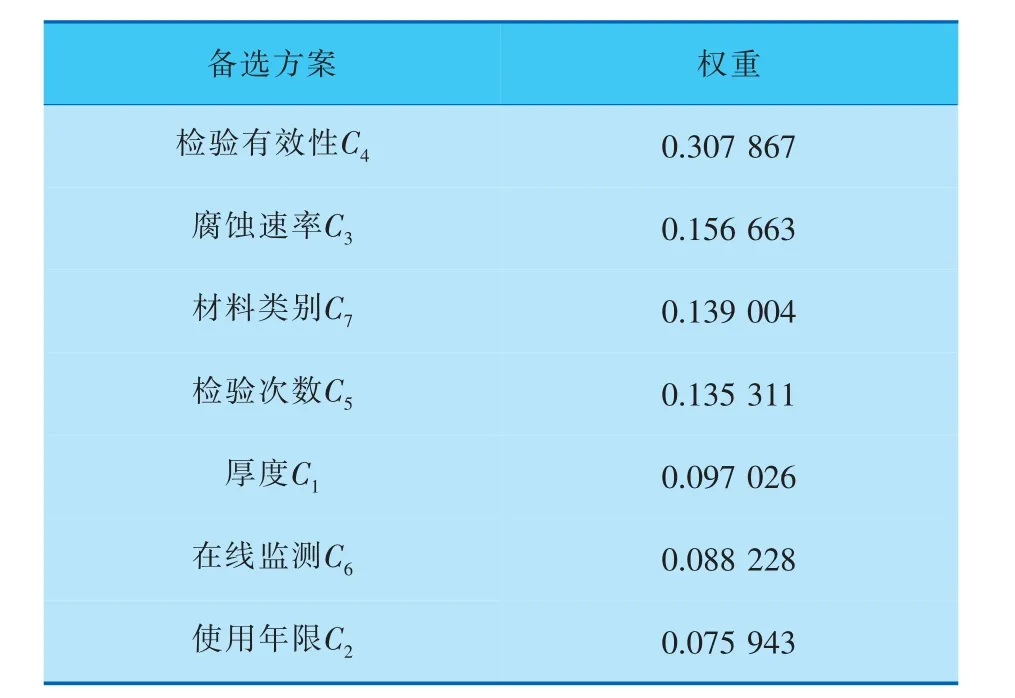
表4 方案层要素对目标层权重排序

2.2 多层次灰色综合评价法进行评价

确定评价灰类的等级数、灰数及白化权函数。

记灰类为e，根据评价等级可知，评价灰类共5类， 相应的灰数为⊗=（⊗1，⊗2，⊗3，⊗4，⊗5）=（9，7，5，3，1），根据表3赋值，选取几名经验丰富的现场技术人员和管理人员的评分，得到D为：

所对应的白化权函数及图像列于表5。

表5 5种灰类所对应的白化权函数及图像

由指标层-准则层-目标层依次计算评价结果，Mi（i=1，2，3，4）的评价结果如下：

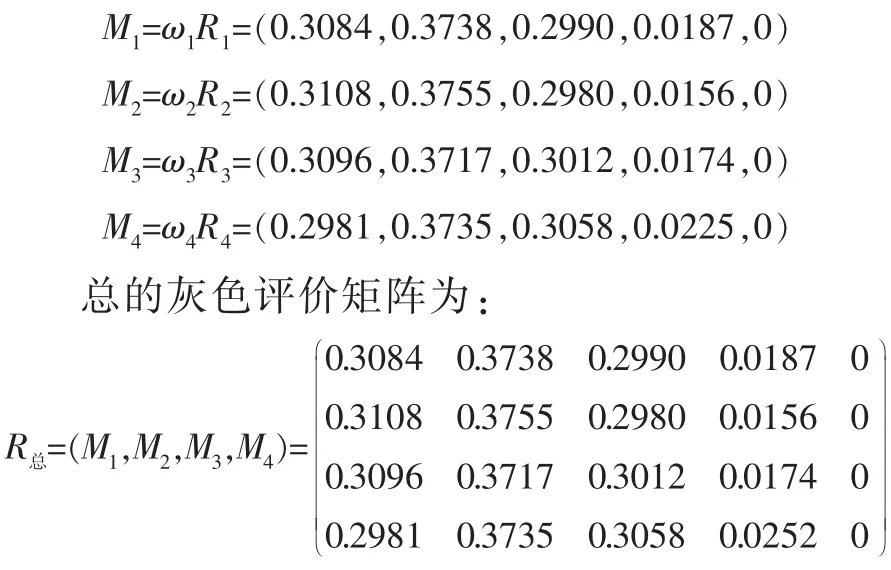
破坏系数综合评价结果为：

M=ωR总=（0.3059，0.3736，0.3011，0.0201，0）

常压储罐破坏系数的修正系数PE=6.9341，取管理系统评价系数为1.0，同类设备失效概率为4×10-5，则该储罐底板的失效概率为0.000 277。 该储罐通过传统RBI风险评估方法和改进方法得到的分析结果见表6。

表6 传统RBI评估方法与改进RBI评估方法风险分析结果对比

与该储罐的漏磁扫描检测数据对比，该储罐的底板有腐蚀现象， 且存在腐蚀深度超过20%的地方，有一定的失效风险。改进的RBI评估结果与储罐的腐蚀损伤真实情况更接近，基于多层次灰色综合的RBI评估方法与传统的评估方法相比准确性更高。

3 结论

3.1 根据多层次灰色综合评价模型，可实现变权的思想，能够根据储罐的不同损伤部位和损伤机理，实时动态地调整系数的权重值。

3.2 将层次分析与灰色理论有机结合，运用于储罐失效概率的计算和风险评价中，不仅可降低单一方法的主观性，使评价结果更加科学、合理，而且对加强常压储罐安全管理、有针对性地解决储罐安全问题具有重要的现实意义。

3.3 将常压储罐多层次灰色综合模型应用到实际案例中，通过验证结果表明，基于多层次灰色综合的RBI评价方法计算失效概率的结果比传统RBI评估方法更加准确。