交变热应力对疏水管焊缝反复开裂的影响

张藤飞 李 喆 吕 涛 陈小萌

（1.江苏核电有限公司；2.西安交通大学能源与动力工程学院）

田湾核电3、4号机组MAL系统蒸汽疏水管道在机组运行中多次发生疏水阀下游三通或弯头处的焊缝开裂问题。 当焊缝开裂位置靠近凝汽器侧或开裂缝较大时， 将会导致凝汽器漏真空，严重影响机组的安全稳定运行［1～4］。 初步分析表明，上述焊缝开裂与机组的疏水阀旁路气动调节阀在正常运行工况下频繁开启有关。 为此， 利用FLIR红外热像仪和应变片对其下游疏水管道外壁状态进行测量，发现气动疏水阀开启和关闭导致下游疏水管道的压力和温度波动，且由于管路不同部位壁厚的不均匀性，使管道温度分布具有不均匀性和时变特性，进而产生周期性的应变和交变应力。 另外，气动疏水阀严重偏离设计运行条件，将加剧下游疏水管道的湿蒸汽冲击，并影响机组的经济性［5～8］。

然而， 由于疏水管内存在高速汽液两相冲击、疏水闪蒸等问题，很难在内壁布置传感器。 为了确定气动疏水阀开启和关闭对下游管路热应力的影响，笔者结合数值模拟对疏水管内温度变化与热应力状态进行研究，进而确定MAL系统蒸汽疏水管道疏水阀下游焊缝反复开裂的失效原因和内在机理。 在此基础上，针对田湾核电3、4号机组MAL系统，提出疏水管路的改进方案，以解决焊缝反复开裂和疏水不畅（旁路气动调节阀频繁开启）问题。

1 基于Abaqus的下游疏水管道交变热应力分析

利用Abaqus软件，对疏水器或气动疏水阀开启前后下游疏水管的热应力状态以及随时间的变化规律进行建模和仿真分析。

1.1 数值计算方法

管道热应力的计算分析主要是通过商业有限元（Finite Element Analysis）分析软件Abaqus完成的。采用全耦合的计算方式来进行，即同时求解应力场与温度场， 这种求解方式相比于顺序耦合方式而言，计算更加节约时间，效率也更高［9～11］。

1.2 计算模型与参数设置

疏水器或气动疏水阀开启时，下游疏水管内汽水混合物高速流动， 并且壁面以饱和水为主，与管道换热强烈；由于外壁有保温层，使管道温度逐渐趋近于管内工质的当地温度。 为了减少管内积水，水平疏水管都有一定的坡度，但由于焊缝内凸环面的存在，当疏水器或气动疏水阀关闭时各管段内仍会残留一些积水。 另外，由于下游疏水管内工质的含水量高达80%以上， 管道内壁必然是湿表面，而且大多数疏水器或气动疏水阀都存在不同程度的泄漏。 因此，疏水器或气动疏水阀关闭后，管内约1/4的积水依靠自身显热瞬间闪蒸（因其换热系数达到饱和水蒸发或凝结的30倍以上）， 温度快速降低到与凝汽器压力对应的饱和温度。 随后，由于管道内壁温度远高于积水温度，湿表面水膜和积水被逐渐蒸发，管壁温度逐渐下降；而在这一过程中，焊缝等内凸部位无积水，湿表面水膜非常薄，可以近似认为是干表面，所以最大热应力通常发生在这一过程中。 建立疏水器下游管道（φ48 mm×4.5 mm）计算模型，利用Abaqus软件对管道热应力进行仿真计算。

1.2.1 模型介绍

首先， 通过三维建模软件CATIA对48 mm带焊缝管道进行建模。图1展示了48 mm带焊缝管道模型。 具体尺寸参数：管壁厚度4.5 mm，模型总长度56.5 mm，焊缝宽度6.5 mm，高度2.5 mm。

图1 48 mm带焊缝管道模型示意图

1.2.2 Property Modulus设置

疏水器或气动疏水阀关闭时，下游疏水管内压力与凝汽器的压力相同，其工质为4 kPa的饱和蒸汽，此时对应的导热系数λ=18.712 mW/（m·K），蒸汽动力黏度为9.826 9 μPa·s。 定压比热容Cp为1.916 7 kJ/（kg·K）， 蒸汽密度为0.028 743 kg/m3。设定疏水器关闭后工质流速达到3 m/s，计算得到雷诺数为342.22，普朗特数为1.006 56，蒸汽与壁面的换热系数为0.72 W/（m2·K）。

在经济厚度和热损失计算中， 可知管道保温结构外表面的放热系数a=11.63 W/（m2·K）（10 kcal/（m2·h·℃））。

管内湿表面水膜和积水受高温管道加热而蒸发，根据水相变换热特性，其换热系数通常为1 500～3 500 W/（m2·K），本研究取2 000 W/（m2·K）。

为探索交变热应力随管道初始温度的变化规律，将疏水器关闭时刻的管道金属温度分别设置为90、110、130、150 ℃，并且沿管道均匀分布进行热应力计算。 另外，按照经验设置保温层内壁与疏水管外壁的初始换热温差为5 ℃。 疏水器与气动疏水阀关闭后下游疏水管内的工质温度按4 kPa饱和蒸汽温度设置为29.11 ℃。

热导率和比热容均会随温度的变化而变化。在进行热应力场的计算时，再增加一个热膨胀系数。实际管道材料为0Cr18Ni9（与0Cr19Ni9类似），查表知，密度为8 000 kg/m3，线膨胀系数取1.76×10-5℃-1。 热导率、比热容参数设置见表1、2。

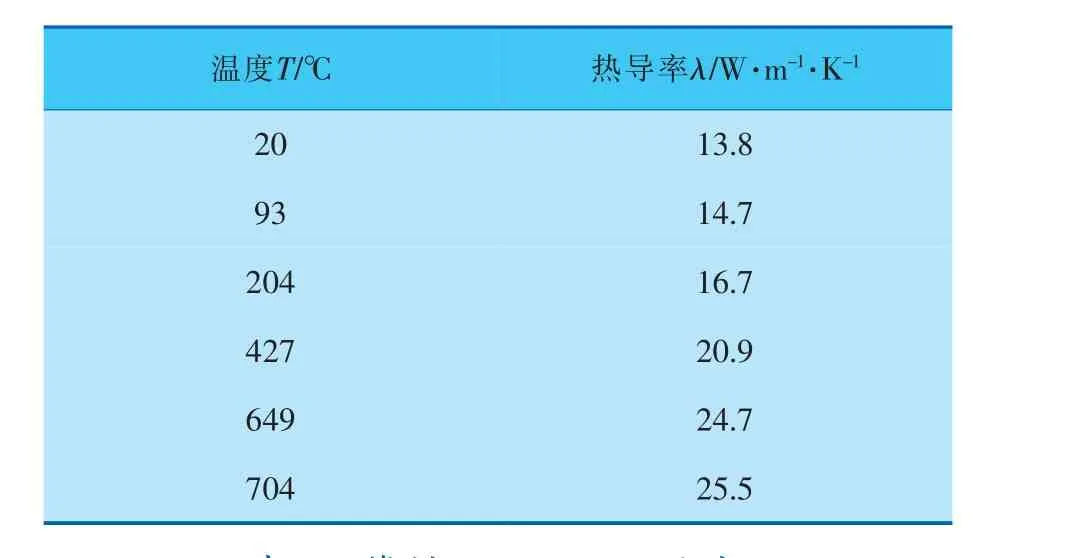
表1 管材0Cr18Ni9热导率

表2 管材0Cr18Ni9比热容

1.2.3 Step Modulus设置

Step中选择的分析步类型为温度-位移全耦合分析步， 所有工况的Time Period初始设置为20 s，Incrementation Type为Automatic。 最大增量步设置为10 000，Initial increment size 设 置 为10-5，Minimum increment size 设 置 为10-15，Maximum increment size设置为2。单位增量步之间允许的最大温差设置为20 ℃。

1.2.4 Mesh Modulus设置

图2为48 mm管道的整体网格划分示意图，除了焊缝部分采用非结构化网格（四面体）之外，其他管道部分均采用六面体结构化网格进行划分。除此之外，由于在管道内外壁面处存在与周围流体换热的现象，为提高计算精度，在靠近管道内外壁表面部分还进行了网格加密。 其中Global size设置为0.6 mm，靠近内外壁面的网格尺寸设置为0.06 mm，图3所示为结构化和非结构化的局部放大示意图。

图2 48 mm管道的整体网格划分示意图

图3 48 mm管道的结构化网格/非结构化网格局部放大示意图

1.3 数值计算结果

1.3.1 48 mm疏水管湿表面水膜热应力计算

图4为初始时刻（0 s）和20 s时的管道温度场分布云图。管道壁面的温度值与应力值大小均是从节点温度值读取得到的，因为内外壁面上的温度场和应力场分布是均匀的，所以随机选择节点读取温度场与应力场即可。

图4 管道初始温度为90 ℃在0 s和20 s时管道的温度场分布云图

图5展示的是48 mm管道初始温度为90 ℃时焊缝处的热应力变化曲线， 图6展示了焊缝最大应力出现时刻管道的温度云图。 疏水器关闭后，由于内外壁面与接触工质热交换的持续进行，管道内部逐渐出现温差，导致了热应力的产生［12～14］。焊缝处与管道壁面的温度差随着焊缝高度的增加而变大，此处的热应力最大值即可代表管道的最大热应力［15～18］。从应力变化曲线可知，应力值随着时间呈现出先增大后减小， 最终趋于平稳的趋势， 最大应力值为87.94 MPa，出现的时刻为0.34 s。

图5 48 mm管道初始温度为90 ℃焊缝处的热应力变化曲线

图6 焊缝最大应力出现时刻T=0.3386 s时管道的温度分布云图

图7展示了管道内壁面和外壁面的温度随时间的变化曲线。 通过对比可知，因为保温层的存在，最终管道外壁面的温度高于内壁面的温度。

图7 48 mm管道内/外壁面温度随时间的变化曲线

管道初始温度为110、130、150 ℃时48 mm疏水管的计算结果同管道初始温度为90 ℃的基本一致，疏水器/气动疏水阀关闭后，由于内外壁面与接触工质的热对流的持续进行，管道内部逐渐出现温差，导致了热应力的产生［19，20］。 所不同的是，因管道初始温度的不同，焊缝处出现的最大热应力的大小和出现的时刻有所不同。

不同初始温度下48 mm疏水管焊缝处热应力最大值的计算结果汇总于表3。 可以看到，焊缝处的最大热应力出现在气动疏水阀关闭后0.34～0.42 s时间段，按平均换热温差100 ℃计算，其单位面积的换热强度约为200 kW，0.5 s将使水膜厚度因蒸发减薄0.033 mm。 由于焊缝内凸结构的影响，对于含水量超过80%的汽水混合物来说，壁面残留水膜厚度足以维持到最大热应力的出现。

另外，出现在焊缝处的最大热应力随管道初始温度的升高而增大，当管道初始温度从90 ℃增加至150 ℃时， 其最大热应力也从87.4 MPa增加到152.6 MPa。 根据焊缝评定标准，取应力集中系数为2.0。 按照频繁开关情况（约每2 min一次）折算实际寿命，结果见表4。 可以看到，管道初始温度为90、110、130、150 ℃时，焊缝上游及下游最大应力均已超过疲劳极限，在达到标准中规定的循环次数条件下，焊缝位置可能产生疲劳裂纹。

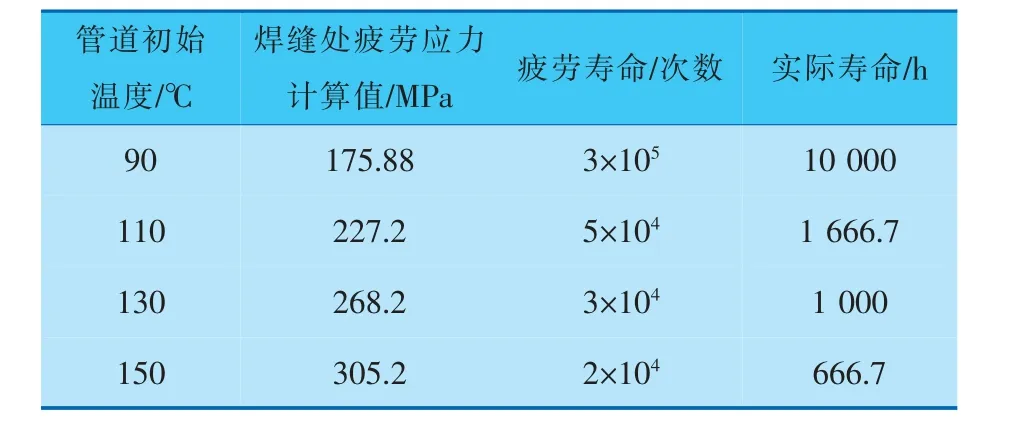
表4 不同管道初始温度下48 mm疏水管的疲劳寿命

1.3.2 疏水管局部积水热应力计算

为了模拟管道局部积水蒸发的热应力状况，建立如图8所示的模型， 图中积水区域主要模拟由管道安装坡度和焊缝内凸高度引起的积水区域。 为了提高计算精度，对积水区域进行了网格加密处理。

图8 48 mm带焊缝部分积水管道模型示意图

积水区域换热系数设置为2 000 W/（m2·K），其余内壁面的换热系数设置为0.72 W/（m2·K）。对管道初始温度为110 ℃时48 mm疏水管的焊缝温度场和应力场进行了模拟。 选择焊缝底部节点的热应力值代表焊缝处的最大热应力。

图9、10分别展示了48 mm疏水管初始温度为110 ℃时的焊缝处应力场随时间变化曲线和应力最大时刻所对应的温度场。 根据结果可知，焊缝处最大热应力为187.6 MPa，相比1.3.1节中的计算结果， 管道初始温度为110 ℃时焊缝处的最大热应力仅为113 MPa。 由此可见，同样管道初始温度下局部积水产生的热应力大约是湿表面水膜产生的热应力的1.5倍。

图9 管道初始温度为110 ℃时焊缝处的热应力随时间变化曲线

图10 管道初始温度为110 ℃时焊缝最大应力出现时刻管道的温度云图

在实际工作中，由于湿表面水膜是必然存在的， 因此并不会出现模型设置的积水区蒸发、其他区域为干表面的现象。 上述计算结果的意义在于，即使湿表面水膜很薄，不足以维持到最大热应力的出现，随后局部积水蒸发所产生的热应力将会造成更严重的破坏，因此，用湿表面水膜蒸发过程来模拟下游疏水管并不会过高估计交变热应力值。

1.3.3 疏水器下游管道不同位置的温度

表5为疏水器开启和关闭后下游管道内部不同位置的温度数据。 观察数据可以发现，在工作过程中，疏水器开启前，管内存留的蒸汽或凝结水温度与凝汽器温度相同，为302.15 K（绝压4 kPa对应的饱和温度）。 疏水器开启瞬间，下游管道的流动阻力和工质压力迅速升高，由于每个位置的工质温度会快速增大到与其位置处压力对应的饱和温度，距离疏水器越远处的温度越高。 当疏水器关闭后，下游管道的流动阻力和工质压力迅速降低，同理每个位置的工质温度会快速降低到与其位置处压力对应的饱和温度，距离疏水器越远处的温度越低，管道末端的工质温度最终会降低到凝汽器温度。 由此可知，疏水器或气动疏水阀的频繁开启和关闭引起的管道交变热应力是造成焊缝开裂的主要原因，且温差和交变热应力随下游疏水管阻力的增大而增大。

表5 疏水器开启、关闭后下游管道内部不同位置的温度数据

2 疏水管道改造方案

综上所述，减少疏水器和气动疏水阀下游疏水管交变热应力是解决疏水管焊缝反复开裂问题的主要途径。 针对田湾核电3、4号机组MAL系统的疏水管道，提出改进方案如下：

a.选择与管路疏水量匹配的疏水器，解决气动疏水阀频繁开启问题，减少因气动疏水阀开启和关闭产生的交变热应力。

b.选择连续排水的疏水器， 如浮球式疏水器，以减少下游疏水管道的温度交变频次。 根据仿真结果， 即使下游疏水管初始温度仅有90 ℃，其产生的交变热应力也会导致管道疲劳破坏。 因此减少疏水器的开关频次是解决疏水管疲劳破坏的最有效途径。

c.从疏水系统和旁路疏水阀安全性考虑，建议选择节流能力更强、安全性更高的阀门作为旁路疏水阀。

d.增大下游疏水管管径、减少流动阻力。 下游疏水管流动阻力越大，管内工质压力对应的饱和温度就越高，其与疏水器或旁路疏水阀关闭后的管内工质温差也就越大，导致下游疏水管的交变热应力增大，疲劳寿命急剧减少。 由此可见增大下游疏水管管径、减少流动阻力是降低交变热应力、提高疏水管疲劳寿命的主要措施。

e.若条件允许， 可更改疏水的最终排放位置，提高疏水器关闭时下游疏水管内压力，缩小管道与水膜温差，从而减小交变热应力，提高管道寿命。

3 结束语

笔者通过对田湾3、4号机组MAL系统蒸汽疏水管道问题的深入分析，详细探究了疏水阀下游管道焊缝开裂的原因和内在机理。 数值模拟揭示了疏水管直径、流动阻力、节流孔板以及疏水背压等多方面因素对疏水管道的交变热应力产生影响，进而造成焊缝异常开裂。 并针对该问题提出了相应的解决建议，可进一步提高疏水管道系统的运行可靠性，为核电机组疏水系统的优化设计与安全运行提供了实质性的参考价值。