基于改进SSA-VMD的列车门丝杠机构故障诊断技术研究

王若凡 杨 柳 李永凯 李思文 朱松青

（南京工程学院机械工程学院，江苏 南京 211167）

0 引言

随着轨道交通行业的发展，客流密度也在不断上升，各类列车门故障不断出现［1］。通过列车门振动信号来分析诊断故障状态，可为列车安全可靠运营提供保障。

目前，对列车门故障诊断的研究相对较少。沈长青等［2］提出一种多尺度卷积类内自适应的深度迁移模型，但未充分考虑在实际运行过程中噪声产生的影响。针对列车门工作时环境噪声大、故障信号易被覆盖、难以提取故障特征信息等问题，需要分析在强噪声下的故障特征提取方法。现有的振动信号降噪方法有经验模态分解（EMD）、集合经验模态分解（EEMD）、变分模态分解（VMD）等。EMD通过选取合适的模态分量来重构降噪［3］，姚玲峰等［4］通过EMD来对丝杠振动信号进行降噪处理，但存在边界效应及模态混叠等问题。集合经验模态分解（EEMD）的指标包含多余的辅助噪声［5］，张培玲等［6］提出改进小波阈值与集合经验模态分解相结合的方法，能提升去噪效果，但依旧无法完全解决模态混叠的问题。变分模态分解（VMD）能有效避免模态混叠问题［7］，其参数设置需要人工进行判断，而不合理的参数组合设置易陷入局部最优。韦海成等［8］通过二次解构来选取K值，但忽略了惩罚因子对分解结果的影响。为解决惩罚因子α和模态分量数K难以选取的问题，学者们提出基于元启发式的参数寻优方法，刘均等［9］提出SSA-VMD 算法来优化关键参数，但容易陷入局部最优。在此基础上，许多学者力求研究性能更好的变体，李爱莲等［10］针对后期寻优能力不足的问题，提出融合正余弦定理的SSA 算法。张伟康等［11］提出基于蝴蝶优化算法的改进SSA 算法。吕鑫等［12］针对前期种群搜索度差的问题，提出Circle 混沌初始化种群的改进麻雀搜索算法，但未能解决后期收敛性差的问题。

已有的研究采用不同策略弥补了SSA 缺点，并取得一定成果，但仍存在寻优性能不足、收敛速度过慢等问题。因此，本研究提出一种基于多策略融合的改进麻雀搜索（SSA）优化VMD 方法。通过Hénon 混沌映射来初始化种群，降低陷入局部最优的可能性，提升个体多样性，将非线性权重因子应用于算法搜索阶段，通过改进个体搜索方式来提升前期全局寻优及后期局部搜寻的能力，使用Levy飞行及柯西变异策略来扩大个体搜索空间，从而增强跳出局部最优能力。通过以上方式对麻雀搜索算法进行改进，并将其与VMD 算法结合，从而实现参数自适应的选取，并获取降噪信号。通过降噪信号提取特征并进行故障诊断，结果证明该方法达到了有效的诊断效果。

1 数据采集

本研究以列车门丝杠机构振动信号为研究对象，以某交通公司提供的列车门系统为基础，搭建故障诊断试验平台，进行开关门试验，试验过程中电机最高转速为4 200 r∕min，采样频率为20 kHz。通过对试验平台门系统的连续开关门，获得丝杠机构故障数据及正常数据。根据靠近振动源方式来安装振动传感器，安装示意如图1所示。

图1 列车门振动传感器安装

2 信号降噪处理

2.1 变分模态分解

Variational Mode Decomposition（VMD）是一种自适应模态分解及信号处理方法，其能解决非平稳信号的模态混叠等现象。通过选取合适的模态分解数和惩罚因子，使用变分模态分解对原始信号进行重构，能起到降低噪声的作用，便于后期故障特征提取。该算法的基本思路是对变分问题的构造和求解，变分表达见式（1）。

式中：K为模态分量数；uk为模态分量；wk为中心频率；∂t为梯度运算；*为卷积运算；F为原始信号。

引入Lagrange 乘子法算子λ来求解约束问题，见式（2）。

式中：α为惩罚因子。

采用交替方向乘子算法来分解原始信号，并进行迭代寻优，见式（3）到式（5）。

式中：γ为噪声容限，设定γ=0 可实现更佳去噪效果。

迭代至满足约束条件，见式（6）。

式中：ò为阈值判定条件。

2.2 麻雀搜索算法

麻雀搜索算法是根据麻雀觅食行为而提出的智能优化算法［13］，利用麻雀搜索算法分别优化变分模态分解的参数K和α，可得到降噪信号。麻雀觅食过程包含发现者及跟随者，发现者寻找食物并散布位置和方向，追随者通过上述位置来确定食物来源。麻雀群体可选择上述两种行为进行觅食。群体中的个体会根据其他行为来争取多的同伴资源，从而提高自身成功率。同时，群体认为危险时会发出预警，并进行反捕食。

拥有高适应度的发现者优先级更高，提供整体觅食位置方向，因此，其搜索范围大。位置更新描述见式（7）。

式中：t为迭代次数；itermax为最大迭代数；α 为（0，1］内的随机数；R2为预警值，R2∈［0，1］；ST为安全值，ST∈［0.5，1］；Q为服从正态分布的随机数；L为元素全为1的1×d的矩阵。

当R2ST时，发现周围有捕食者，发出警报，并移动至安全位置觅食。

追随者位置更新描述见式（8）。

式中：XP为发现者最优位置；A为元素随机为±1 的1×d的矩阵；Xworst为发现者最差位置；A+=AT（AAT）-1，A+为伪逆矩阵。当i>n∕2时，此时饥饿的第i个追随者飞向其他位置获取食物。

危险时群体的反捕食描述见式（9）。

式中：Xbest为全局最优位置；K为移动方向，也为控制参数，K∈［-1,1］；β为步长参数；fg、fw分别为全局最优和最差适应度；fi为个体适应度；ò为最小常数，防止分母为0。

2.3 麻雀搜索算法的改进

2.3.1 Hénon 混沌映射初始化种群。标准的麻雀优化算法初始种群是随机生成的，导致后续搜索容易出现位置分布不均，陷入局部最优。通过更改初始化策略来提升麻雀搜索算法的运行效果，更好的初始解有助于提升迭代效率。采用Hénon 混沌映射来提升种群初始化分布的均匀性，增加个体多样性，可提升整体寻优能力［14］。初始化种群策略见式（10）。

式中：t为迭代次数；a、b为可调节参数。

混沌序列能遍历整体搜索空间，最优混沌序列见式（11）。

对Hénon 混沌序列y1（t），根据式（11）逆映射得到麻雀位置，见式（12）。

式中：z（t）为最优混沌序列；ubi、lbi为搜索空间的上下限。

使用Hénon 混沌映射并设置参数（a=1.4、b=0.3），得到强随机性混沌序列，分布如图2所示。

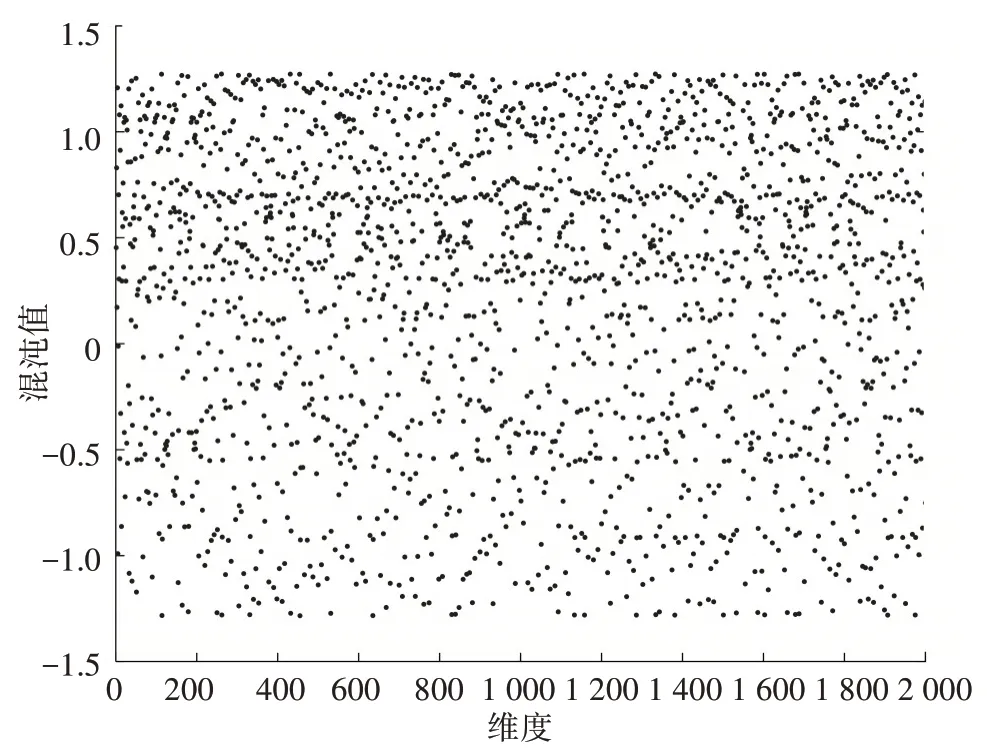
图2 Hénon混沌映射分布

2.3.2 非线性权重因子。在分析算法模型后发现，麻雀发现者对种群的依赖度较高，易受到当前位置的影响。通过引入非线性权重因子来改进发现者更新公式［15］，调节历史速度对新迭代的影响，降低前期个体对搜索的影响，可提升全局最优搜索能力，提升后期个体依赖程度，加快收敛速度。非线性权重因子见式（13）。

式中：t为当前迭代次数；T为最大迭代次数。

对发现者位置更新公式进行改进，见式（14）。

2.3.3 Levy 飞行策略。使用自然界移动模型、模拟行为策略来加强小范围信息挖掘能力，用Levy飞行策略来改进麻雀搜索算法。Levy 飞行是生物种群的自然捕食策略，在小步长间隙出现大步长，能增加整体步态的随机性，在交替探索过程中，采取不同长度搜索距离来寻找全局最优解［16］，改进后的表示见式（15）。

式中：d为向量维度。

Levy的计算见式（16）、式（17）。

式中：Γ（x）=（x-1）！；Q为服从正态分布的随机数；r3、r4∈［0,1］；ξ为可调节常数，本研究取值为1.5。

2.3.4 柯西变异。针对麻雀优化算法易陷入局部最优的问题，通过柯西变异来增强种群寻找全局最优的能力，能有效跳出局部最优值的限制。其分布函数原点处峰值较小但在两端分布广，利用此特点来脱离局部最优，能更好达到全局最优［17］。标准柯西分布函数见式（18）。

个体在经过变异后，通过短时间搜索周围区间将搜索重心转移至全局最优，整体寻优算法具有良好的调节能力，能增强种群多样性，搜索过程中产生距离较远的随机数，使用更新公式对全局最优解进行变异处理，见式（19）。

式中，Cauchy（0，1）为标准柯西分布函数。

2.4 基于改进SSA-VMD的信号降噪处理

信号熵值越小，序列复杂度越低。使用改进的SSA 算法来优化变分模态分解所需的参数组合，选取样本熵为适应度函数［18］，最终得到最优的参数组合。基于改进SSA优化VMD的流程如图3所示。

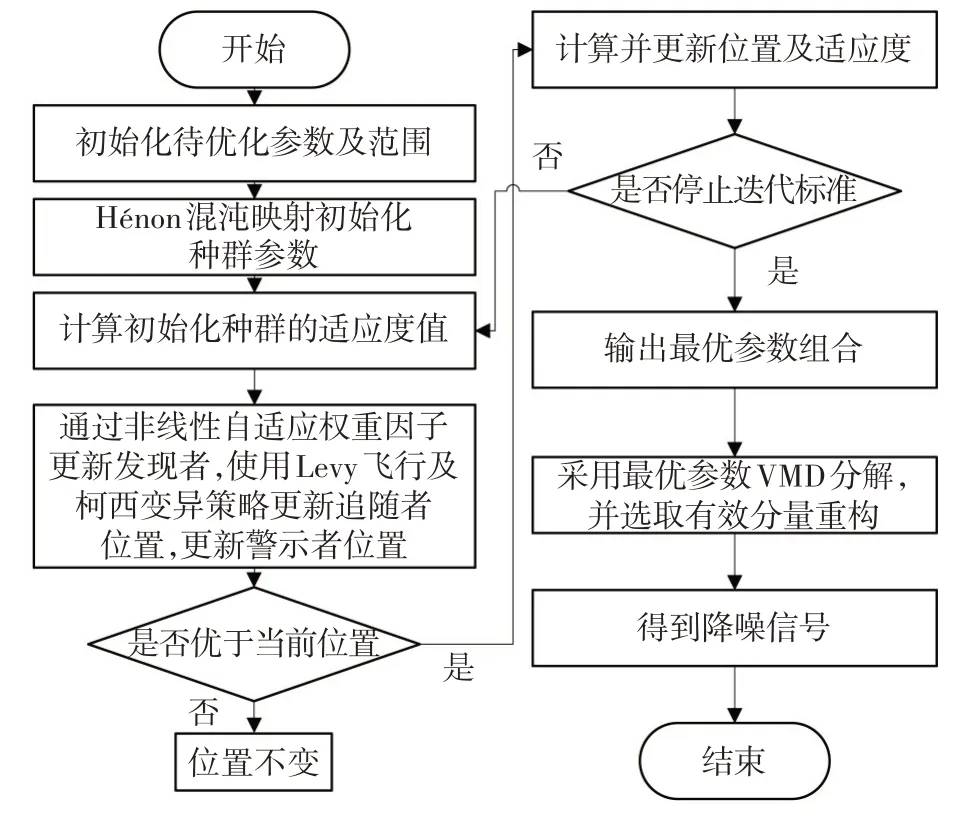
图3 改进SSA算法优化VMD方法流程

对采集到的含噪信号，使用改进SSA-VMD 方法进行处理，将样本熵设为适应度函数，对参数组合寻优，迭代曲线如图4 所示。得到最佳模态分量数为8、惩罚因子为2 048，将参数组合带入到相应公式中，分解得到降噪信号。

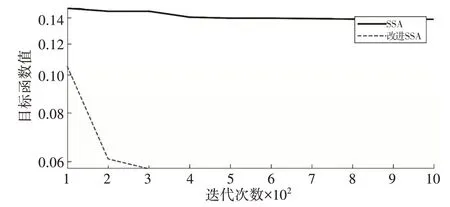
图4 迭代寻优

为验证方法的有效性，与其他方法进行对比，并以降噪后的仿真信号信噪比（SNR）系数为评价标准。各类方法的信噪比系数见表1。本研究提出的方法通过对模态分量数和惩罚因子的自适应选取，能更好地去除噪声。

表1 不同算法降噪性能指标

以某交通公司提供的地铁列车门系统为例进行验证，得到驱动机构故障数据。通过对本研究所提出的算法优化后的组合参数进行模态分解，降噪效果明显。结果如图5所示。

图5 信号去噪前后对比

3 基于主成分分析的综合特征提取

提取信号方差、均方根值、峭度值等时频域特征量，并进行主成分分析［19］，由新的五个主元组成的特征集方差累计贡献率超过95%，这充分体现出原始数据的重要信息，实现特征降维。方差贡献如图6所示。

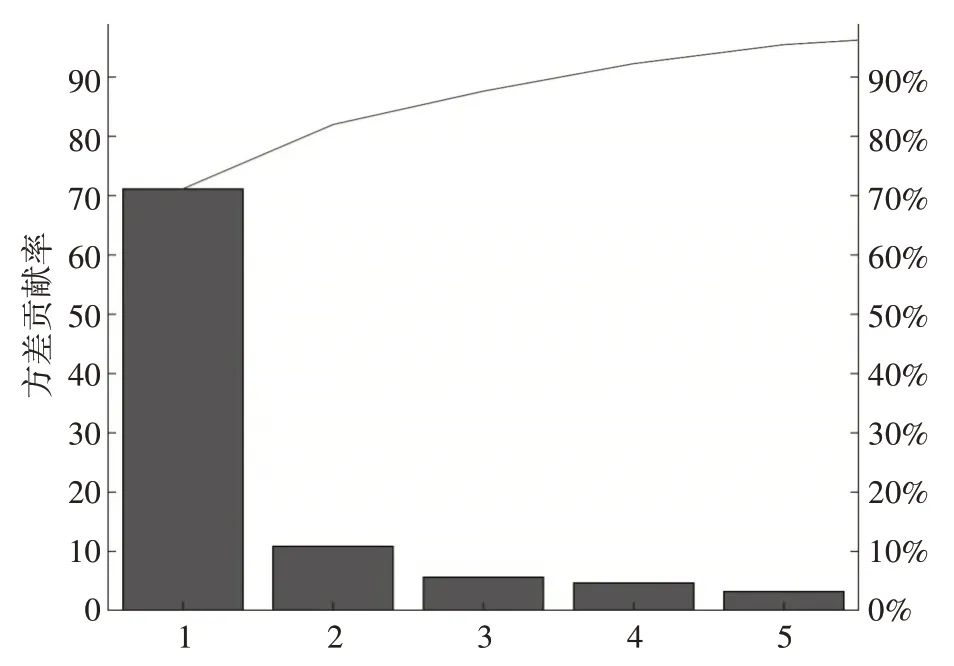
图6 主成分分析方差贡献

4 SVM故障诊断

对试验过程中得到的机构状态进行分类，分为丝杠机构故障、正常运行状态。分别从两类状态特征信号中各自选取100 个特征信号样本点作为训练集，对SVM 模型进行训练［20］。选取100个样本点作为测试集，使用经过训练的SVM 模型对测试集进行分类预测，得到故障分类的准确率为91%，从而验证故障诊断方法是有效的。改进后的SSAVMD-SVM测试分类效果如图7所示。

图7 改进SSA-VMD-SVM 测试分类效果

5 结论

①针对列车运行过程中因噪声过大导致难以准确提取故障特征等问题，通过将麻雀搜索算法与变分模态分解结合，对不同信号自适应选取变分模态分解最佳参数组合，可避免出现人为选取导致分解不当等问题，降低了列车门在运行过程中产生的大量噪声，为后续健康状态分析提供理论基础。

②针对麻雀搜索算法迭代后期容易陷入局部最优等问题，提出多策略融合法对SSA-VMD 方法进行改进，在种群初始化阶段引入Hénon 混沌映射，在算法搜索阶段引入非线性权重因子，使用Levy飞行及柯西变异策略来改变个体搜索行为，对难以确定的参数组合进行自适应选取。

③改进SSA-VMD 方法的降噪指标优于小波类降噪、奇异值差分谱法及原始麻雀搜索算法，从而验证了改进SSA-VMD 方法的有效性，该改进方法具备明显优势。

④试验结果表明，改进的SSA-VMD 故障诊断方法在一定程度上克服了种群初始化的盲目性，提高了算法跳出局部最优解及进行全局搜索的能力，使用主成分分析法能有效提取故障特征，并通过支持向量机模型分类，结果表明，改进后的算法具有一定优势，可实现对列车门丝杠机构故障的精确诊断。