亲缘选择下间接互惠的量子鹰鸽博弈模型合作演化稳定性

张新立,王新颖,程 程,付子芮

(辽宁师范大学 数学学院,辽宁 大连 116029)

0 引言

自2005年《科学》提出了“合作行为如何演化是21世纪最关键的25个科学问题之一”以来[1],研究合作行为的演化稳定性一直是国内外学者重点关注的问题。Smith和Price[2]创立的演化博弈论及Nowak[3]提出的五大合作机制为研究合作行为演化稳定性提供了有效的理论框架。在二人博弈中,鹰鸽博弈被广泛使用,很多学者利用该理论对鹰鸽博弈合作演化稳定性进行了研究,其中以五大合作机制中亲缘选择和间接互惠最为常见。亲缘选择是指愿意与血缘关系近的伙伴合作的合作机制,如家族企业。Hines和Smith在具有亲缘关系的鹰鸽博弈中得到混合演化稳定策略的概率分布不同于纯策略的概率分布[4]。Seidy和Ale等人分别从静态和动态角度展示了合作(鸽)策略为演化稳定策略时,亲缘关系满足的条件[5,6]。间接互惠是人们的善意或恶意不能直接回报,而被传递了不相关的第三方的合作机制,如慈善企业。Nowak和Sigmund利用间接互惠的评分系统,得到玩家知道对家得分的概率必须大于成本效益比,双方才能达到合作[7,8]。Berger建立间接互惠的容忍度评分规则,表明对背叛者有一定的容忍度,可引导社会稳定合作[9]。

上述文献虽然已经从完全理性发展到了有限理性,但在参与人支付函数方面,并没有突破经典博弈建立的理论范式。亲缘选择或间接互惠虽然能使个体间形成合作演化均衡,但很难回答这样一个问题:由于合作系统内部的个体间争夺公共资源,必然为资源的有限性发生冲突,导致合作解体,鹰鸽博弈困境仍没有解决。由Meyer[10]创立的量子博弈论为解决这个困境提供了有益思路。王斌等人给出了一个新的量子策略纳什均衡并达到帕累托最优,解决了鹰鸽博弈困境[11]。Sun[12]等人通过改变纠缠度使量子鹰鸽博弈达到了合作。

基于上述在演化博弈理论下研究合作行为演化稳定性的不足及量子博弈的优势,本文首先运用量子博弈刻画了鹰鸽博弈参与人支付函数,然后把亲缘选择和间接互惠有机结合起来,建立亲缘选择下间接互惠的量子鹰鸽博弈合作演化模型,求出了博弈的演化稳定策略(ESS),对亲缘选择、间接互惠和纠缠如何影响博弈合作进行了分析。此理论不仅拓展了传统博弈模型支付函数的表示形式,而且把两种合作机制与量子博弈结合起来,在两种合作机制和量子纠缠的统一框架下,解决人类竞争和冲突等问题,具有重要指导意义。

1 模型的假设与建立

1.1 量子博弈模型的建立

假设博弈中参与人是两个有限理性主体,分别为参与人I和参与人II,双方都有两个可选择的策略合作(鸽)策略D和背叛(鹰)策略H.假设双方共同获取某一收益为B,双方发生冲突付出的成本为C,且C>B>0.则经典鹰鸽博弈的收益矩阵为[13]:

参与人II

DH

(1)

(2)

1.2 亲缘选择下间接互惠量子鹰鸽博弈模型的建立

(3)

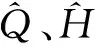
(4)

2 模型均衡点与演化稳定性分析

2.1 模型均衡点

(5)

(6)

(7)

类似可计算参与人II的收益,进而得到参与人I、II的复制动态方程分别为:

(8)

(9)

2.2 均衡点稳定性分析

引理1[15]均衡点为演化稳定策略(ESS)当且仅当其复制动态方程的雅可比矩阵满足DetJ>0和TrJ<0条件。

分别对F(x)与F(y)求偏导可得雅可比矩阵:

(10)

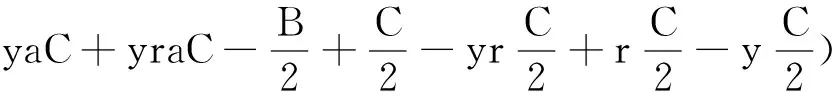
(11)

(12)

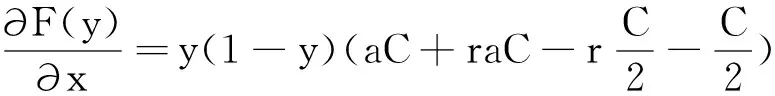
(13)

(14)

根据Friedman提出的均衡点稳定性判定准则(引理1),对上述五个均衡点进行稳定性分析有如下结论成立:

定理1 均衡G1(0,0)点不稳定。

证明:均衡点G1(0,0)的Jaconbian矩阵为

J(G1(0,0))=

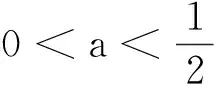
证明:均衡点G2(0,1)的Jaconbian矩阵为

J(G2(0,1))=

令DetJ(G2(0,1))>0,TrJ(G2(0,1))<0得

由于博弈收益矩阵是对称的,对均衡点G3(1,0)稳定分析后,可得到相同结论。

证明:均衡点G4(1,1)的Jaconbian矩阵为

定理4 均衡点G5(x*,y*)为鞍点。

证明:均衡点G5(x*,y*) Jaconbian矩阵对角线元素为0,故TrJ(G5(x*,y*))=0.因此均衡点G5(x*,y*)为鞍点。

2.3 合作影响因素分析

由图1可知根据参与双方的初始概率不同系统有三种演化结果:(1,1)(1,0)和(0,1).鞍点构成了这三种收敛结果的临界线,当参与双方开始博弈的初始概率在临界线右上方时,系统稳定于(1,1),二人选择合作。可见鞍点(x*,y*)是博弈演化路径的重要影响因素,现考虑鞍点对合作的影响。x*和y*越接近0,右上方趋近(1,1)的概率越大,双方决定合作的概率越大。

图1 博弈演化路径图

1) 纠缠度

2) 辨别度

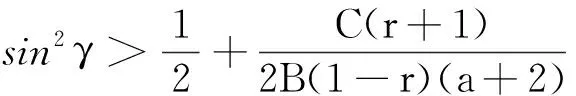
3) 相关度

3 数值仿真

仅从理论层面对模型进行分析推导,无法直观地反映各参数对博弈合作的影响,因此本文利用MATLAB软件数值分析纠缠度γ、相关度r和辨别度a对参与人I合作演化的影响。对参与人II的影响与参与人I相同,设置初始状态(0.2,0,4)、B=2、C=3.

图2、3、4分别为参与人I选择合作的概率随纠缠度γ、相关度r、辨别度a变化的情况。当a=0.1时,必须保证sin2γ≥0.5参与人才会选择合作并趋于稳定;当a=0.6时,sin2γ=0.1参与人就会选择合作并保持稳定。由此可见量子纠缠度是正向促进合作的,若辨别度较大,纠缠度较小,双方也会合作。当sin2γ=0.6,a=0.1或sin2γ=0.1,a=0.6时,较低的相关度也会使双方合作;当a=0.1,sin2γ=0.1时,要求r≥0.8才会合作,相关度越大越有利于合作。当sin2γ=0.1时,a≥0.4才会合作;当sin2γ=0.6,纠缠度较大,辨别度即使很小,双方也会稳定合作。符合本文的理论分析部分,由以上分析可见纠缠度、辨别度和相关度均会正向促进合作,为使参与双方合作,应增加三参数的值。

图2 纠缠度γ对合作的影响

图3 相关度r对合作的影响

图4 辨别度a对合作的影响

4 结论