基于PASCO转动运动传感器测量刚体转动惯量

齐敬强,刘梦林

(北京交通大学 威海校区 实验中心,山东 威海 264401)

刚体转动惯量是描述刚体转动时惯性大小的物理量。常用的刚体转动惯量的测量方法有扭摆法[1]、三线摆法[2]和落体法[3]等。落体法测量刚体转动惯量(以下简称落体法)是利用力矩、角加速度和转动惯量之间关系,通过测量力矩和角加速度从而计算出转动惯量的方法。落体法的实验原理比较简单,易于理解,但是实验误差相对较大。很多学者从不同的方面分析了落体法的实验误差并进行了改进[4-7]。在落体法实验中如何精确地测量出转动系统的角加速度是非常关键的步骤,在此之前大部分的测量方法都是通过计时计数器记录不同时刻载物台转过的角度,然后计算出转动系统的角加速度[8-9],这种测量方法较为复杂且误差较大。

PASCO实验平台是一个集数据收集、应用和分析于一体的物理实验系统。传感器采集数据后,计算机可以对过程中的数据进行处理,尤其是对一些瞬态变化的物理量能够做到实时测量[10-11]。利用PASCO转动运动传感器可以直接测量出物体转动时角速度随时间变化的数据,并且可以直接得出转动物体的角加速度。通过这种方法可以简化落体法的实验步骤,从而提高实验精度。

1 实验装置

图1为实验装置图。实验中用到的装置主要包括转动惯量实验仪(ZKY-ZS)、转动运动传感器(PS-2120)及支架、850通用接口(UI-5000)、一台装有PASCO Capstone软件的计算机、游标卡尺、天平、圆盘试样、圆环试样、圆柱试样、细绳和砝码。

图1 实验装置图

2 实验原理

刚体的定轴转动定律为

M=Jβ。

(1)

其中M为刚体转动时所受的总合外力矩,β为该力矩作用下刚体转动的角加速度,J即为刚体的转动惯量。只要测量出刚体转动时所受到的总合外力矩M及该力矩作用下刚体转动的角加速度β,即可计算出该刚体的转动惯量J。

如图1所示,在落体法实验中,力矩M的大小为

M=TR,

(2)

其中,T为细绳的拉力,R为绕线塔轮的半径。将细绳的一端系上质量为m的砝码并将细绳绕过转动运动传感器,然后将细绳的另一端缠绕在半径为R的绕线塔轮上,系统在恒外力矩的作用下做匀加速转动。若砝码的加速度为a,则细绳所受到的拉力为

T=m(g-a) ,

(3)

其中,g为重力加速度,g=9.8 m/s2。若此时载物台的角加速度为β,则砝码的加速度为

a=Rβ。

(4)

为了方便计算,先假设系统的阻力矩为零,由(1)(2)(3)(4)式可得:

(5)

为了计算圆盘、圆环和圆柱试样的标准转动惯量,下面列出具体计算公式。标准圆盘和圆柱绕中心轴旋转时的转动惯量计算公式为

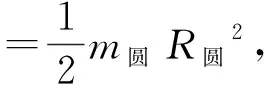
(6)

其中,m圆为圆盘或圆柱的质量,R圆为圆盘或圆柱底面的半径(以下简称圆柱的半径)。

标准圆环绕中心轴旋转时的转动惯量计算公式为

(7)

其中,m环为圆环的质量,R内为圆环的内圆半径,R外为圆环的外圆半径。

根据平行轴定理可知,物体围绕通过质心O的转轴转动时的转动惯量最小。当转轴平行移动一段距离后,绕新转轴转动的转动惯量为

J平=J0+m0d2,

(8)

其中,J0为物体围绕通过质心O的转轴转动时的转动惯量,m0为物体的质量,d为转轴平行移动的距离。

3 实验过程

3.1 实验准备

将细绳一端不重叠地密绕在直径为5 cm的塔轮上,然后将细绳绕过转动运动传感器的滑轮,在细绳的末端悬挂砝码。转动运动传感器通过850通用接口接入计算机。打开PASCO Capstone软件,设置时间t为横坐标,单位为秒(s),设置角速度ω为纵坐标,单位为弧度/秒(rad/s)。转动运动传感器的滑轮直径为4.78 cm,而塔轮的直径为5 cm,两者的角速度不同,但是成一定的比例。通过PASCO Capstone软件的计算器功能,可以将滑轮的角速度乘以两者的比例系数即可将滑轮的角速度转化为塔轮的角速度。

3.2 测量并消除阻力矩

在实验原理的推导中为了计算方便,我们假设阻力矩为零,但是在实际的实验过程中阻力矩不为零,我们需要测算出阻力矩并消除其对实验的影响。在细绳的末端从小到大放置不同质量的砝码,轻轻推动载物台直至载物台能够匀速转动,此时砝码产生的力矩刚好可以抵消阻力矩。在计算刚体转动惯量时,只需要将这一部分砝码的质量减去即可。通过多次实验,确定大约1 g砝码产生的力矩刚好可以抵消系统的阻力矩,此时实验系统近似处于平衡状态。为了验证实验的准确性,在细绳末端悬挂1 g砝码,分别在载物台上不放试样和放置不同的试样,轻轻推动载物台,通过PASCO Capstone软件记录角速度随时间变化的数据。

3.3 测量试样的转动惯量

将细绳不重叠地密绕在直径为5 cm的塔轮上,在细绳的末端悬挂30 g的砝码。载物台上不放任何试样,此时为空载物台。释放砝码,细绳带动空载物台和转动运动传感器加速旋转,通过PASCO Capstone软件记录角速度随时间变化的数据。将实验装置恢复到初始状态,在载物台上分别放置圆盘试样和圆环试样,重复以上的步骤,分别记录角速度随时间变化的数据。将实验装置恢复到初始状态,将两个质量相同的圆柱对称地放置在距离载物台中心为9 cm的位置,重复以上步骤,记录角速度随时间变化的数据。

3.4 测量试样的基本参数

使用天平分别测量圆盘、圆环和圆柱试样的质量。使用游标卡尺分别测量圆盘和圆柱试样的半径以及圆环试样的内外半径。

4 实验数据及分析

4.1 验证实验系统的平衡状态

通过多次测试可得,在细绳末端悬挂1 g砝码时,系统近似处于平衡状态。图2为不同实验条件下系统的平衡状态图。在平衡状态时,空载物台及载物台上放置圆盘、圆环和圆柱试样后系统转动时的角加速度分别为0.006 75 rad/s、-0.001 72 rad/s、-0.001 25 rad/s和-0.001 80 rad/s。在实验测量时,细绳末端挂30 g砝码,空载物台及载物台上放置圆盘、圆环和圆柱试样后的角加速度分别为1.197 rad/s、0.743 rad/s、0.620 rad/s和0.820 rad/s。平衡状态时的角加速度与实验测量时的角加速度的比值分别为0.56%、-0.23%、-0.20%和-0.22%。平衡状态时的角加速度远小于实验测量时的角加速度,因此近似认为载物台系统是匀速转动。由此可以得出质量为1 g的砝码产生的力矩近似可以抵消系统的阻力矩。

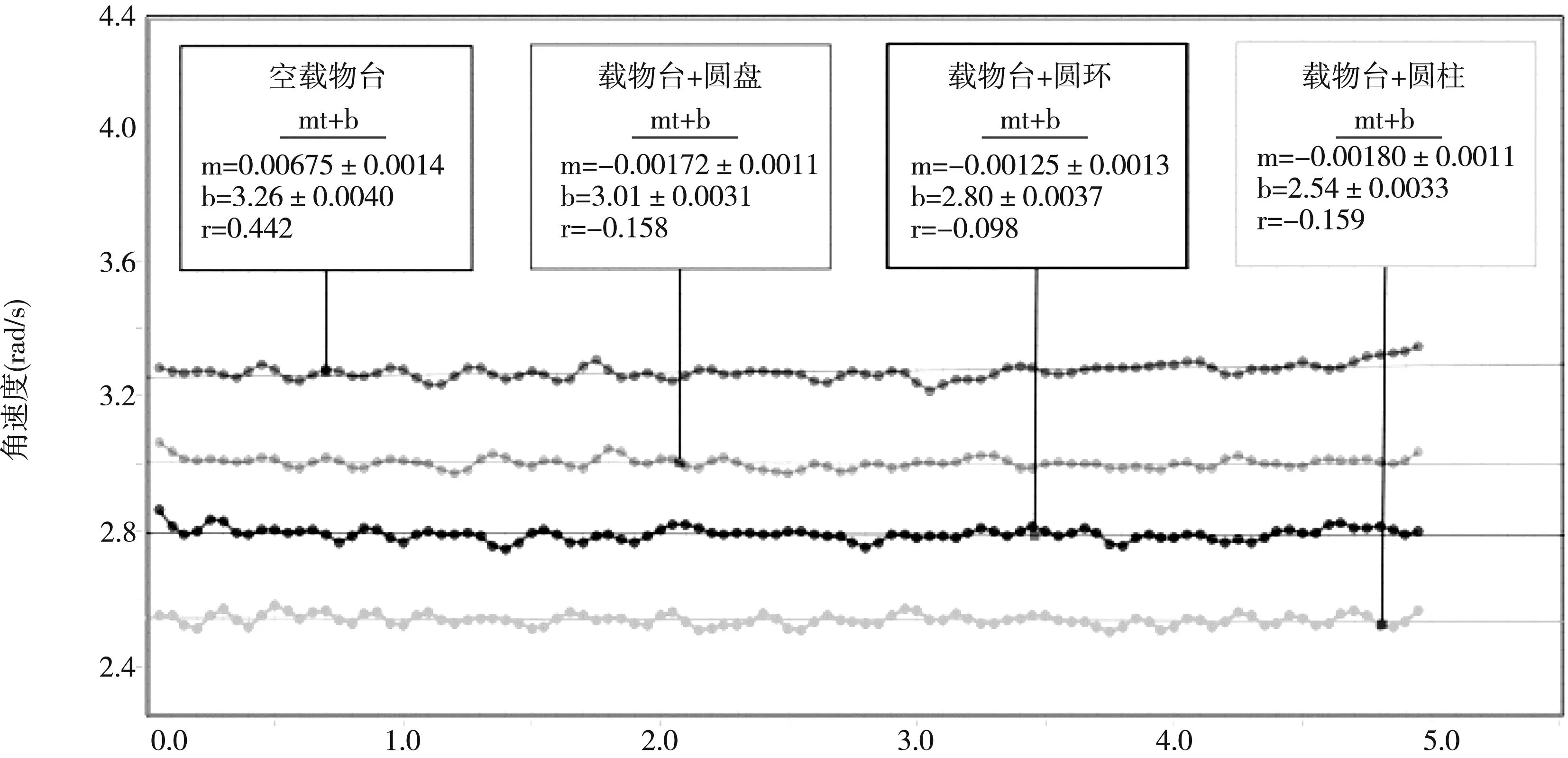
图2 不同实验条件下系统的平衡状态图

4.2 计算试样的转动惯量的实验值

图3为不同实验条件下角速度变化的图像。空载物台及载物台上放置圆盘、圆环和圆柱试样后的角加速度分别为1.197 rad/s、0.743 rad/s、0.620 rad/s和0.820 rad/s。前面已经给出1 g砝码用来抵消系统的阻力矩,因此砝码的有效质量为29 g。已知塔轮的半径R为2.5 cm,砝码的质量m为29 g,角加速度β由图3可得,将以上数据代入(5)式可得空载物台的转动惯量为5.918×10-3kg·m2,圆盘加载物台的转动惯量为9.545×10-3kg·m2,圆环加载物台的转动惯量为1.1442×10-2kg·m2,圆柱加载物台的转动惯量为8.647×10-3kg·m2。因此圆盘的转动惯量为3.627×10-3kg·m2,圆环的转动惯量为5.524×10-3kg·m2,圆柱的转动惯量为2.729×10-3kg·m2。

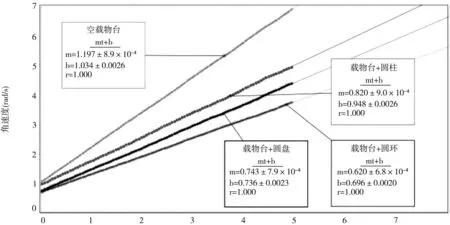
图3 不同实验条件下角速度变化图像

4.3 计算试样的转动惯量的标准值

已知圆盘的质量为503.7 g,直径为239.82 mm,由(6)式可得圆盘的转动惯量的标准值为3.621×10-3kg·m2。已知圆环的质量为431.5 g,内圆直径为209.90 mm,外圆直径为240.16 mm,由(7)式可得圆环的转动惯量的标准值为5.487×10-3kg·m2。已知两个圆柱的总质量为331.2 g,圆柱的直径为30.00 mm,圆柱平移的距离为90.00 mm,由(6)式和(8)式可得圆柱的转动惯量的标准值为2.720×10-3kg·m2。

4.4 计算相对误差

表1列出了圆盘、圆环和圆柱试样的转动惯量的实验值和理论值,通过计算可得三组实验的相对误差分别为0.2%、0.7%和0.3%,三组实验的相对误差都小于1%,实验数据准确。

表1 不同试样转动惯量的相对误差

5 结 论

将PASCO转动运动传感器与刚体转动惯量实验仪相结合,用PASCO转动运动传感器通过PASCO Capstone软件直接测量物体转动时的角加速度,简化了实验步骤,让实验操作更便捷,有利于学生更好地完成实验。用改进后的实验装置进行实验,实验结果的相对误差都在1%以内,实验精度很高,教学效果良好。