基于局部熵的级联故障模型初始负载定义方式

董 昂,吴亚丽,任远光,冯梦琦

(西安理工大学 a.自动化与信息工程学院;b.陕西省复杂系统控制与智能信息处理重点实验室,西安 710048)

0 引言

社交网络,电力网络,生物网络等复杂网络是当今社会的重要组成部分[1],其复杂性体现在真实网络海量的节点及节点之间复杂的连接关系。在复杂网络中,节点和边承担的负载是不断演化的,具有一定的动力学特征。当节点或边的负载大于自身容量而导致失效后,失效节点或边的负载通过网络的相互连接被重新分配到相关节点或边上,从而引起其他节点或边失效,产生级联效应,严重时会导致整个网络的瘫痪,这种由微小事件引发的连锁故障称为级联失效。现实生活中存在许多级联故障问题,例如:运输网络级联失效[2]、装备保障网络级联失效[3]、电力网络抗毁性分析[4]、局域路由器级联问题[5]等。建立普适性的级联故障模型,研究其动力学特性,已经成为预防和控制级联故障的有效手段[6]。

近年来,级联故障模型的研究集中于节点初始负载的定义,节点容量的定义以及故障节点负载的分配方式[7]3个方面。文献[8]假定网络中的信息通过节点之间的最短路径传递,因此利用介数定义节点的初始负载,并提出初始负载和容量呈线性关系,建立了经典的ML模型。该模型能完整体现级联故障过程,其容量分配方式也得到广泛使用。文献[9]定义网络中每个节点的初始负载为其介数的幂函数。但介数作为一个全局量,在网络拓扑高度复杂的情况下,计算需要耗费很大的算力。因此基于介数的初始负载定义方式不适合用于大规模复杂网络;基于此,文献[10]假定每个节点的初始负载相互独立,并在区间[Lmin,Lmax]上服从均匀分布。采用这种完全随机的初始负载定义方式虽然简便,但是没有利用网络的结构信息。文献[11-13]分析了节点的度和初始负载的相关性,并使用节点的度定义其初始负载。如何充分利用网络的拓扑结构信息已经成为定义初始负载的有效方式。

熵的概念是由德国物理学家克劳修斯于1865年提出,最初是用来描述“能量退化”的物质状态参数之一,在热力学中有广泛的应用。随着统计物理、信息论等一系列科学理论的发展,当人们认识到熵的本质是一个系统“内在的混乱程度”时,它在控制论、概率论、数论、天体物理、生命科学等领域都有了重要的应用。文献[14-15]最早将熵引入图论中,提出了图熵的概念,并认为它能够反映网络的拓扑信息;文献[16]采用图中的一些不变量,如顶点个数、节点的度等信息来计算图熵,并用信息函数来表示概率分布。文献[17]采用节点的度作为非负整数元组来计算p,进而计算图熵。文献[18]中提到了多种图熵的定义方式,不同的图熵在不同的场合下均作为一种度量,依据网络的拓扑结构来衡量节点包含信息量的多少。基于此,本文针对级联故障问题的特点,综合考虑节点及其邻居的信息,提出了一种基于局部熵的初始负载定义方式,在减少计算量的同时,可以更好地模拟网络中的级联过程。通过比较在不同网络中采用介数、度、局部熵定义初始负载的3种级联故障模型面对不同类型攻击时的鲁棒性,验证本文提出局部熵概念的通用性及有效性。

1 基于度和介数的级联故障初始负载定义

一个网络通常由G=(V,E)建模,其中V为网络G的节点集合,E为网络G的边集合。对于一个无向无权网络,可以由一个邻接矩阵A表示。其中,A中的元素Aij的含义为

(1)

节点的度是与它直接相连的边的数目。将节点vi的度表示为di,可以用邻接矩阵的方式表示为

(2)

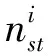
(3)

目前,级联故障模型中节点初始负载多用节点的介数和度进行定义。文献[9]和文献[11]分别采用了两种定义方式。

(4)

(5)

其中,α为负荷系数。

节点的度是节点的特征之一,直接用节点的度定义其初始负载,简单方便但没有考虑其邻居节点信息。介数是一个全局量,它体现了节点在信息流通中的重要性,但在复杂网络中计算介数需要耗费巨大的算力。因此本文引入局部熵的概念,同时考虑节点及其邻居节点的信息来定义节点的初始负载,与介数定义相比大大降低了计算量。

2 局部熵的相关定义

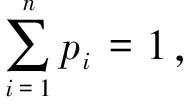
(6)

在图熵中,对于一个网络G=(V,E),pi可以被定义为信息函数f的比值[16]:

(7)

p1+p2+…+p|V|=1

(8)

其中,f(vi)为节点vi的信息函数。

文献[16]提出:信息函数f的定义并不唯一,其本质要能够反映拓扑结构的信息。在网络中,节点vi的度di描述了节点vi与其邻居节点的连接关系,因此本文使用节点的度定义信息函数。节点vi包含全局信息的熵Ei可以通过式(9)计算:

Ei=-pilogpi

(9)

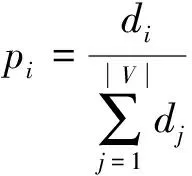
对于一个网络G=(V,E),定义节点vi的第k层邻居节点集合为Sk(vi,G)。

Sk(vi,G)={v∈V|l(vi,v) =k}

(10)

其中,l(vi,v)为节点vi与节点v之间的最短路径长度,1≤k≤diamG(diamG是网络直径)。

整个网络G可以看作由节点vi及其diamG层邻居节点构成,每层邻居对节点vi的贡献不同,应对节点vi的各层邻居提供的信息赋予不同权值。因此更新后的节点vi包含全局信息的熵定义为

(11)

其中,c1,c2,…cdiamG是呈指数递减的正实数序列。

节点vi及其第k层邻居节点的熵LE(vi,k)为

LE(vi,k)=-p(vi,k)logp(vi,k)

(12)

(13)

因此,节点vi的k级局部熵可以定义为

(14)

文献[17]认为节点vi对越接近它的节点影响越大,并对其第三层及以后的邻居节点的影响可以忽略不计,即对vi包含信息量影响最大的是其前两层的邻居节点。为了减少计算量,并使节点vi包含更多的信息,本文在建立级联故障模型时充分考虑节点及其单层邻居节点的信息。

3 基于局部熵的级联故障初始负载定义

3.1 基于局部熵的级联故障模型概念

本文在定义节点的初始负载时,利用信息熵的概念定义了网络中节点的1级局部熵,考虑了节点及其1层邻居节点的拓扑信息。定义节点vi的初始负载为

Li0=LEα(vi,1)

(15)

其中,α为负荷系数。

节点容量的定义采用与ML模型相同的方式,即节点容量与节点初始负载呈线性关系,具体如式(16)所示:

Ci= (1 +T)Li0

(16)

其中,T为容忍系数,且T≥0。T值越大时,节点的容量越大,因此网络抵抗攻击能力越强,鲁棒性越强。但T又是与成本有关的量,当T值越大时,消耗的成本也会越大。

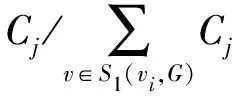
Lj=Lj+ΔLj

(17)

(18)

由定义可知,若节点vj更新后的负载值Lj大于节点vj的容量值Cj,则节点vj故障,并开始级联过程。

Lj+ΔLj>Cj

(19)

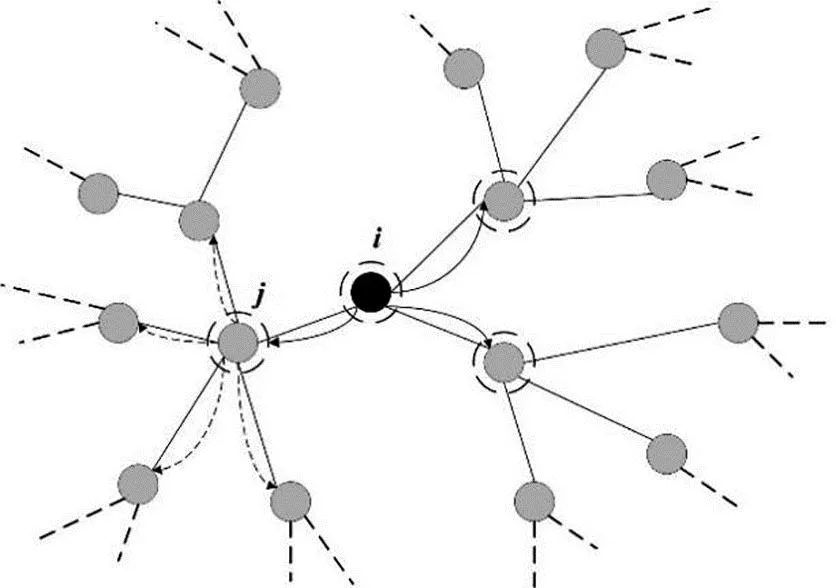
图1 级联过程节点负载分配示意图

据此,可以得到归一化衡量故障指标:设网络中初始故障节点集合为Sf,级联过程结束后的故障节点集合为φf,归一化衡量故障规模的指标计算公式为

(20)

CF越小,网络的故障规模越小,即网络抵抗攻击的能力越好。

3.2 模型解析

为了更清楚地描述模型含义及模型与参数之间的关系,本文通过理论分析对模型进行解析。

由式(19)知,如果节点vi故障,其邻居节点vj从节点vi得到故障负载,与节点vj当前负载之和大于节点vj的容量时,节点vj故障即发生级联故障。因此,当满足式(21):

Lj+ΔLj≤Cj

(21)

时级联故障不会发生。

将式(18)代入(21)可得

(22)

由于节点的容量是由节点的初始负载线性表示,因此将式(16)代入式(22),可得

(23)

整理后可得

(24)

当节点vj的初始负载Lj0=0时,其容量Cj也为0,那么节点vj无意义且不参与级联过程。因此本文仅考虑节点初始负载Lj0>0的情况。

由于Lj0>0,因此,式(24)两边同时除以Lj0,可得

(25)

整理得

(26)

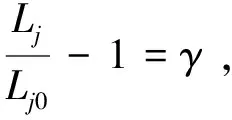
整理可得

(27)

式(27)反映了两个影响级联过程的因素(容忍系数T和节点vi邻居节点的初始负载)之间满足的关系。随着T增大,级联现象减弱或消失;节点的初始负载的定义一定程度上也会影响级联过程。

4 仿真分析

本节通过多个仿真及对比实验,验证了本文提出的基于局部熵的初始负载定义的有效性。

4.1 实验数据集

本文数据集的4个网络均是无向无权的真实网络,具体信息来自网站http://konect.cc/和斯坦福数据库。网络结构的详细数据如表1所示。其中Jazz网络是一个音乐家合作网络,每个节点代表一个音乐家,连边表示两个音乐家之间存在合作关系;Email网络是一个邮件网络,每个节点代表一个人,连边表示两个人之间的通信关系;Hamsterster网络是社交网站Hamsterster中用户之间的关系网络;US.Power网络是美国西部电力网络。表中Nodes、Edges、AveDeg、MaxDeg、AveCluCo分别为网络节点数、网络连边数、网络平均度、网络最大度、网络平均集聚系数。

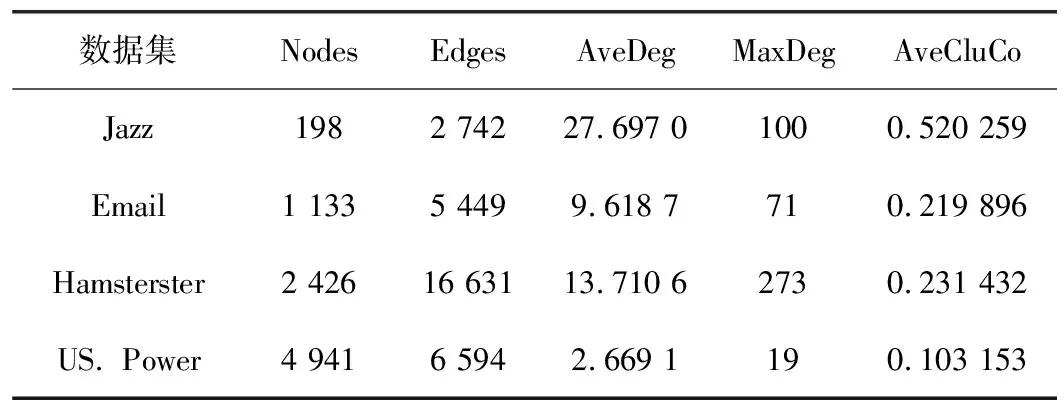
表1 实验网络及其拓扑性质

4.2 攻击策略介绍

本文采用两种类型的攻击策略。

1)攻击单个度最大的节点,即选取网络中度最大的节点作为初始故障节点并开始级联过程。

2)时序攻击是指从选择的初始故障节点集合中,逐个攻击。本文在时序攻击的前提下,从度由大到小排序后的节点集合中选取10%数量的节点进行攻击。4.3节仿真结果表示,选择网络5～10%数量的节点进行攻击,能够更加清楚地体现级联过程。

4.3 仿真结果及分析

本文以Python为编程语言进行仿真。

4.3.1 负荷系数α对网络故障规模的影响

由于真实网络结构复杂多变,其度分布可能不服从幂率分布,因此本文利用Python软件中的Networkx库,生成参数N=1 000,m=2的BA无标度网络进行验证。进行20次独立仿真实验,结果取平均值,仿真结果如图2所示。

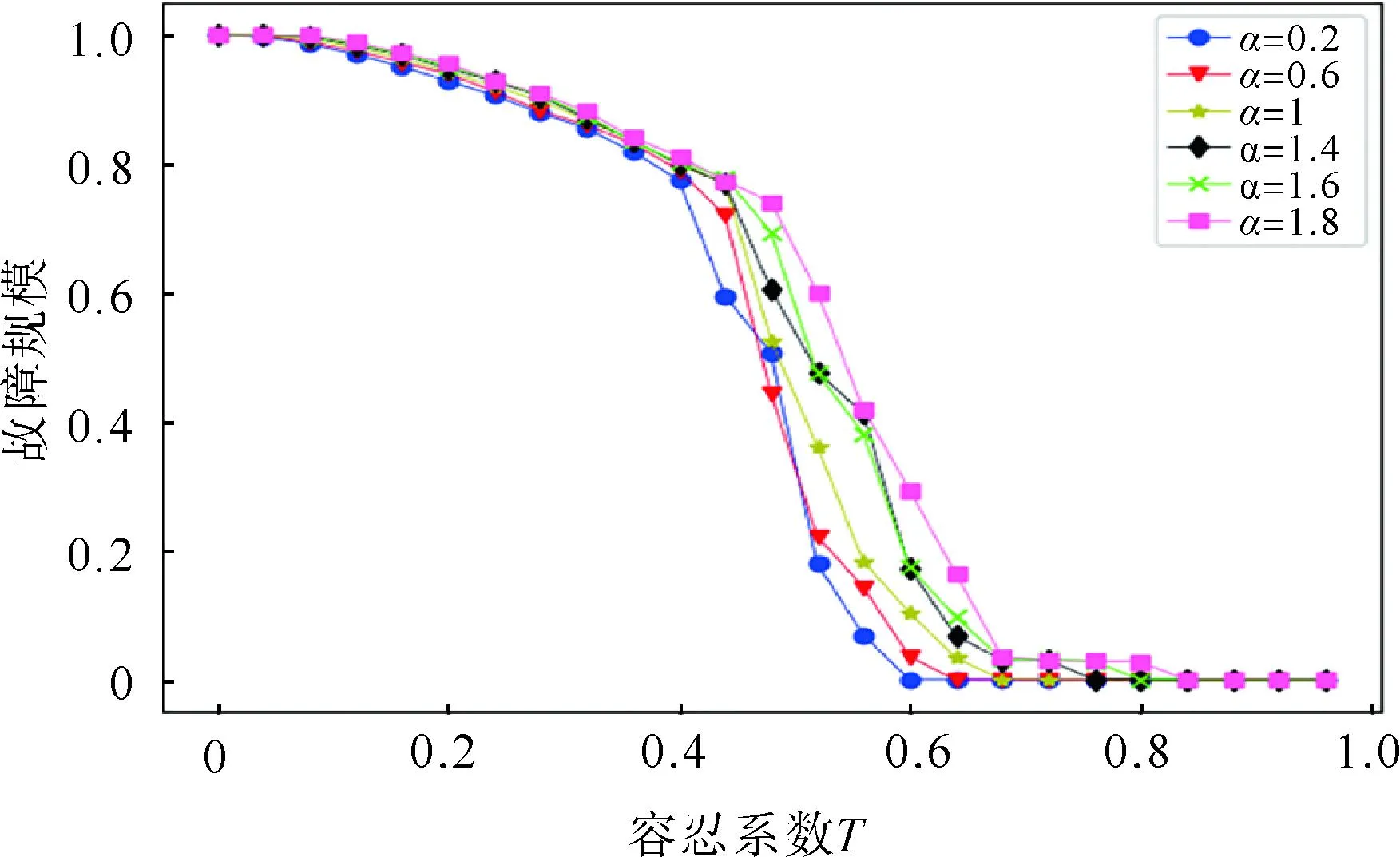
图2 负荷系数α对级联故障规模的影响

图2中,在容忍系数T从0增大的过程中,随着负荷系数α增大,网络的故障规模逐渐增大,网络抵抗蓄意攻击的能力变差。文献[20]认为负荷系数α控制着网络初始负荷的分布,α越大,初始负荷分布越不均匀,仿真结果也验证了这个结论。为了方便研究,本文在比较3个模型时,取负荷系数α=1。

4.3.2 蓄意攻击节点数量对级联过程的影响

选择蓄意攻击节点的数量的多少对级联过程有着不同的影响。以Jazz网络为例,本文分别选择该网络中5%、10%、15%、30%数量的节点进行攻击,仿真结果如图3。

图3 不同数量蓄意攻击节点的级联故障

仿真结果表明:当选择蓄意攻击的节点数目过多时,3种级联故障模型的区别将不再明显。因此选择网络5%～10%数量的节点进行攻击,能更加清楚地对比3种模型的级联故障规模。本文在对比实验中选择网络数量10%的蓄意攻击节点。

4.3.3 不同节点的初始负载定义下级联故障模型对比

本节分析3种不同节点初始负载定义的级联故障模型在不同攻击下的对比效果。

图4是选择单个度最大节点的攻击策略时的对比结果。可以看出:在4个不同的网络中,3种模型的网络故障指标CF,在随着容忍系数T由0增大过程中,从最大值突变为最小值,即级联过程结束后,网络中由全部节点失效转变为没有故障节点产生。仿真结果也体现了容忍系数的含义,当容忍系数T越大,网络中所有节点的容量越大。因此T在从0增大的过程中,有一临界值Tc,当T>Tc时,面对初始攻击,网络中将不会出现级联故障。同时从图4中可以看出,基于节点局部熵定义初始负载的级联故障模型,在容忍系数T更小时,网络中没有故障节点出现,即临界值Tc最小。这说明本文所提出的初始负载定义方式能够以更小的代价提高网络抵抗蓄意攻击的能力。

图4 攻击单个度最大节点的级联故障

图5是时序的蓄意攻击下的仿真结果。与图4不同,图5选择了网络中10%数量的初始失效节点数目,因此网络故障指标CF的值,在随着容忍系数T由0增大的过程中,呈现递减趋势。比较3种模型,从图5中可以看出,基于节点局部熵定义初始负载的级联故障模型,网络故障指标CF的值在随着容忍系数T增大的过程中,下降最快,并且在相同容忍系数T下,网络级联过程结束后的故障规模更小,同样验证了本文提出的基于局部熵的初始负载定义的优势。

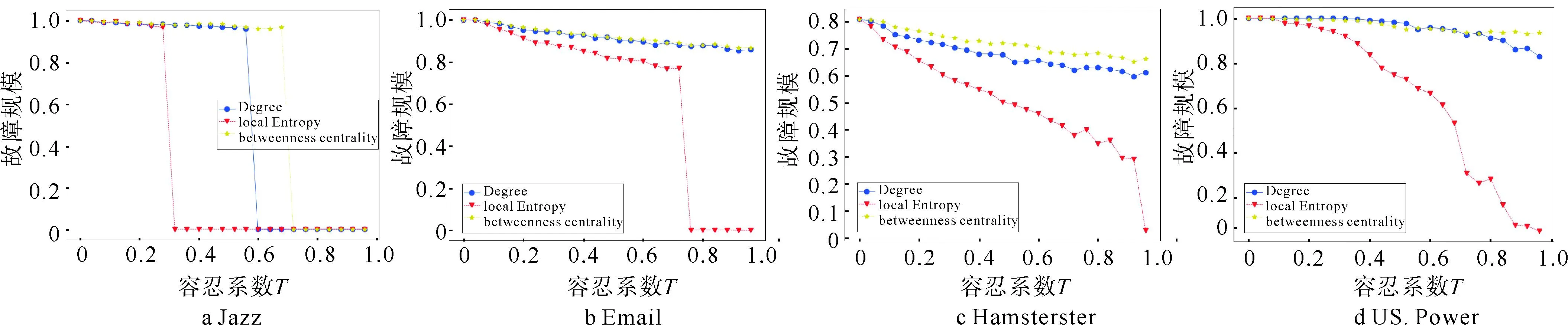
图5 时序蓄意攻击下的级联故障

4.3.4 对式(27)的仿真验证

3.2节通过对模型的解析,我们得到级联过程同攻击节点的初始负载与其邻居节点初始负载比值有关,比值越小,级联故障越不容易发生。本节计算了3种初始负载分配方式下攻击网络中度最大的节点的比值(见表2)。从表2中可以看出基于局部熵的级联故障模型在4个网络中的比值都最小,进一步验证了本文提出的局部熵概念的有效性。

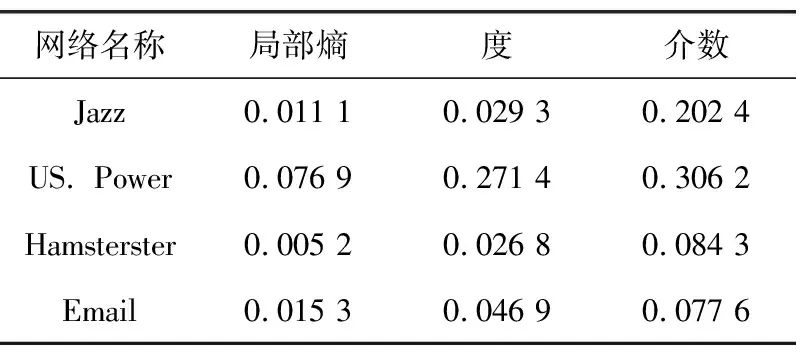
表2 度最大节点的初始负载与其邻居初始负载之和的比值

4.3.5 与传统WK模型的比较和改进

文献[21]在ML模型的基础上提出了WK模型。两种模型主要区别在于节点容量的分配方式。ML模型给每个节点相同的容忍系数T,使得每个节点容量大于其初始负载,这样整个网络的鲁棒性能够得到提高。然而现实生活中,节点容量的分配有一定的限制要求即成本是有限的。WK模型定义容量Ci=(1+T·θ(Li0/Lmax-β))·Li0,其中θ(x)是一个二值函数θ(x)=0(1),x<0(x>0)。在相同容忍系数T的情况下,影响节点容量大小的主要因素有两点:1)节点初始负载的大小;2)参数β的取值。节点初始负载值越大,β取值越小,则节点就会被分配额外的容量,当β=0时WK模型退化为ML模型。因此,在容量成本有限制的情况下,WK模型更倾向于保护初始负载值更大的节点,为此可能牺牲一部分网络的鲁棒性。

本文提出的局部熵模型在ML模型的基础上对节点的初始负载进行了新定义,而WK模型中节点初始负载为节点的介数。对于节点容量分配方式,本文采用与ML模型相同的分配方式。

受WK模型的启发,考虑到节点可分配的容量有限,在本文模型的基础上采用WK模型中的节点容量分配方式,与原模型进行对比仿真验证。以Email网络和US.Power网络为例,攻击策略采用蓄意攻击网络中10%数量的节点,仿真结果如图6。

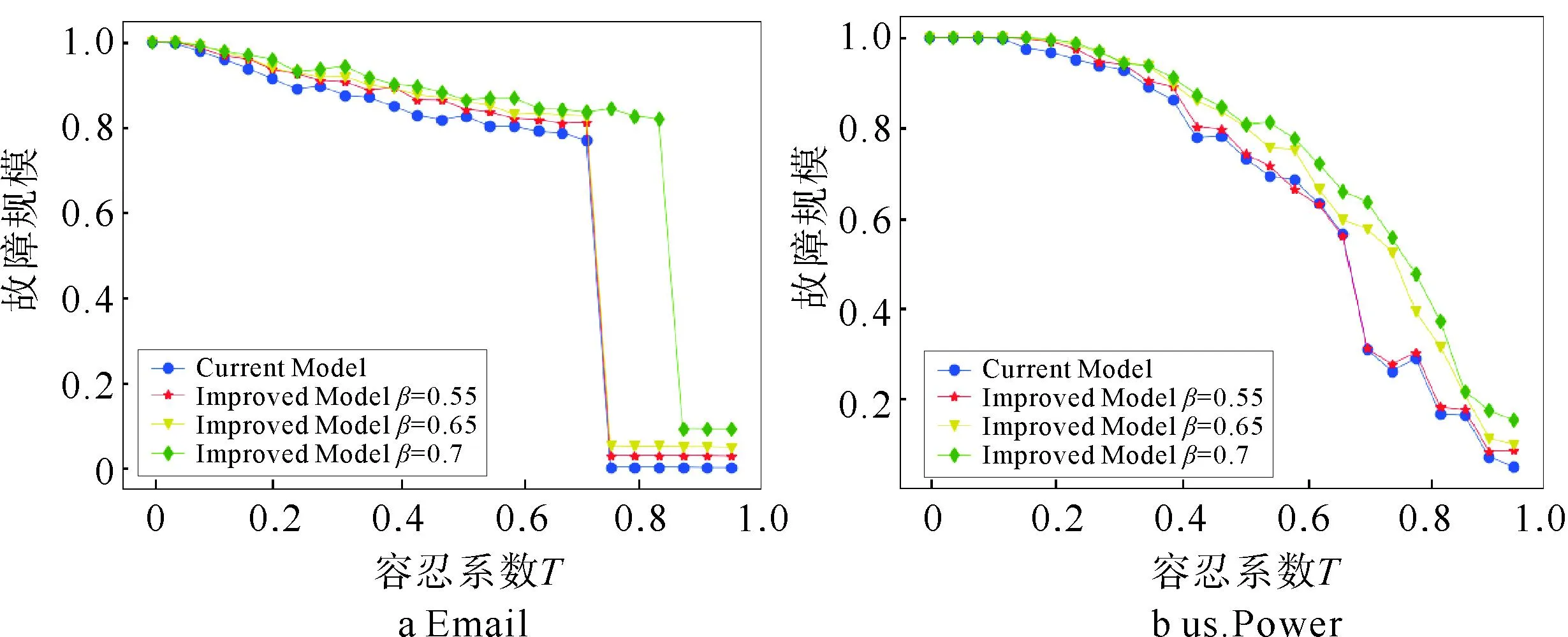
图6 采用WK模型容量分配方式模型后的级联故障对比

从图6可以看出采用原模型的网络,抵抗蓄意攻击的能力最强。采用WK模型的节点容量分配方式后,对于Email网络,当β=0.28时,网络故障规模和原模型近似,此时网络中有28个节点未被赋予额外的容量,即减少了成本,但牺牲了部分网络的鲁棒性。随着β增大故障规模变大,网络抵抗蓄意攻击的能力变差。对于US.Power网络,当β=0.55时,与原模型得到的结果近似,此时网络中44个节点未被赋予额外的容量。仿真结果表明,随着网络规模的增大,可以对更多的节点不赋予额外的容量,以减少更多的成本。在容量有限制的情况下,改进后的局部熵级联故障模型能够以牺牲部分网络鲁棒性为代价,从而减少成本,给予决策者更多的选择。

5 结论

复杂网络作为多学科交叉的新兴学科,在网络化、信息化、数据化的时代,备受研究者的关注。级联故障作为复杂网络的热点研究领域,对我们的日常生活、电力安全等方面有着重要的意义。本文将图熵的概念引入到级联故障模型的节点初始负载的定义中,综合考虑节点及其邻居节点的信息,根据网络中节点的局部熵定义节点的初始负载。在面对两种不同的蓄意攻击时,通过在多个真实网络上对级联故障模型进行仿真分析,结果表明本文所提的基于局部熵的级联故障模型的鲁棒性更好,能够以较小的成本抵抗蓄意攻击。从图熵的角度考虑,保护局部熵较大的节点,也是一种较好的预防级联故障的方式。