电子起爆条件下雷管布置对爆破振动频谱的影响研究*

周俊汝,卢文波,蔡路军,吴 亮

(1.武汉科技大学 理学院,武汉 430065;2.武汉大学 水资源与水电工程科学国家重点实验室,武汉 430072)

钻孔爆破是水利水电工程建设、矿产资源开采等领域最常用的大规模、高效益的破岩方法,却不可避免伴随一些负面效应[1-3],其中以爆破振动为首,是工程设计者和管理者最为关注的爆破安全问题。爆破地震波传播诱发的爆破振动通常利用振动强度、主频和持续时间三个要素描述其特性[4]。工程实践中有资料记载,中远区振速低于安全允许标准时仍有出现低频振动失稳的情况,这说明爆破振动频率对于控制和评价爆破振动危害非常重要。

通过现场爆破试验得知电子起爆中雷管的布置对爆破振动频率具有一定程度的影响,然后利用ANSYS/LS-DANA数值模拟方法,更系统地研究雷管起爆位置和数量对爆破振动频率的作用规律,并从爆源叠加角度,通过分析不同工况中的爆炸荷载特征,探究雷管布置通过改变爆轰传爆方向,进而对爆破振动频率的影响机理。

1 丰宁抽水蓄能电站单孔爆破试验

1.1 工程背景与试验方案

丰宁抽水蓄能电站位于河北省丰宁满族自治县,装机容量3600 MW,分两期工程开发建设。为论证二期工程地下洞室爆破开挖施工对一期工程的影响,结合现场施工条件,在二期地下厂房探洞底板合适部位进行了爆破试验。见图1。

本次爆破试验分两排钻设了6个竖直浅孔,孔深3 m,堵塞0.9 m,孔径42 mm,药径32 mm。第一排的三个孔采用中点起爆,第二排孔采用孔底起爆。这里,为排除自由面对爆破振动频率的影响,将Ⅱ-1号孔作为参照孔,Ⅰ-3号作为试验孔,两孔除雷管布置外其余爆破参数和边界条件完全相同(见图2)。炮孔布置、装药结构与雷管布置如图3所示。

Ⅰ-1:一个自由面 1;Ⅰ-2:两个自由面;Ⅰ-3:两个自由面;Ⅱ-1:两个自由面;Ⅱ-2:三个自由面;II-3:四个自由面图2 逐孔起爆过程中各孔的临空面示意图Fig. 2 The schematic diagram of the free face of each hole in the process of hole-by-hole initiation

图3 爆破试验设计示意图(单位:m)Fig. 3 Schematic diagram of blasting test design(unit:m)

试验中地板上沿探洞纵向中轴线布置6个振动监测点,如图3所示。测试系统采用三维速度传感器,记录仪器为TC-4850爆破振动智能监测仪,其监测振速范围为0.001～35.4 cm/s,振动频率在1～500 Hz。

1.2 现场试验结果分析

对采集的振动信号进行频谱分析,获得爆破振动特征频率,由于主频在爆破地震波传播过程中的衰减有突变或波动[18],这里特征频率除主频外,另选用质心频率表示幅值谱在频域内分布规律,质心频率的定义为[14]

(1)

式中:fc为质心频率;Ai为频率fi所对应的振动速度谱幅值。

本次试验的实测爆破振动信号显示,无论是水平径向、水平切向还是竖直向,主频随爆心距的增大出现较大的波动,衰减规律呈现较大离散性,但可以看出中点起爆振动主频是高于孔底起爆振动主频;质心频率呈现较好的衰减规律,且与雷管布置有较好的相关性。为量化比较雷管布置对爆破振动频率的影响,这里定义频率全局增量来描述其他雷管布置方案相较于底部起爆对频率的影响。

(2)

式中:GFIN是频率全局增量;f是其他雷管布置方案的质心频率;fbottom是底部起爆的质心频率;r是爆心距。

图4显示了中点起爆Ⅰ-3号孔和底部起爆Ⅱ-1号孔两种工况对应的爆破振动频率的衰减规律,中点起爆的爆破振动频率衰减曲线基本位于孔底起爆频率衰减曲线的上方,这说明中点起爆对应的爆破振动频率在全局上要高于孔底起爆对应的爆破振动频率。与孔底起爆相比,中点起爆爆破振动频率的全局增量GFIN在水平径向、水平切向和竖直向三个方向上分别为1.98%、12.67%和5.01%。

图4 Ⅰ-3和 Ⅱ-1号两孔爆破振动特征频率Fig. 4 The eigenfrequency of blasting vibration of Ⅰ-3 and Ⅱ-1

丰宁现场试验实测数据表明起爆位置对爆破振动频率确有一定程度的影响,但对于孔深3 m的两个孔影响不大。对比孔底起爆,中点起爆将起爆点移动到装药段的中点位置,实际上该起爆点同时引爆了上下两部分装药段。

2 不同雷管布置的单孔爆破数值计算

由于爆破试验数据有限,且受地质与周围环境影响较大,试验结果呈现出离散性。这里采用有限元ANSYS/LS-DANA软件建立三维有限元单孔爆破模型,在炮孔几何参数与炸药参数不变的情况下,分析不同起爆点位置与数量对爆破振动频率的影响规律。

2.1 计算模型与参数

考虑对称性,建立四分之一单孔爆破模型,岩体模型尺寸为32 m×32 m×8 m,孔深3 m,其中装药长度为2.1 m,堵塞段0.9 m,孔径42 mm,药径32 mm,下部保留岩体厚度为5 m。在岩体模型的对称边界上施加对称约束,计算过程中除地表为临空面外,其余方向均施加无反射边界以模拟半无限岩体。数值计算模型及测点布置如图5所示。

图5 有限元数值模型Fig. 5 Finite element numerical model

计算中炸药采用MAT_HIGH_EXPLOSIVE_BURN材料模型,结合JWL状态方程计算炸药爆炸过程中压力与体积的关系,表达式如下

(3)

式中:P为JWL状态方程决定的爆轰产物的压力;V为相对体积; 为初始比内能;A、B、R1、R1和ω均为描述JWL方程的独立常数。见表1。

表1 炸药计算参数Table 1 Calculation parameters of explosives

岩体采用MAT_PLASTIC_KINEMATIC材料模型,参数列于表2。

表2 岩体计算参数Table 2 Calculation parameters of rock mass

柱状药包采用空气不耦合装药结构,模型中空气采用MAT_NULL材料模型,同时结合下式的多线性方程描述空气的作用

P=C0+C1μ+C2μ2+C3μ3+(C4+C5μ+C6μ2)e

(4)

式中:C0=C1=C2=C3=C6=0;C4=C5=0.4;μ=ρ/ρ0,ρ,ρ0分别为初始与当前的材料密度。

2.2 数值计算结果分析

对同一个有限元模型,根据雷管布置设置5种雷管布置工况:孔底起爆(雷管布置于药卷底部)、孔口起爆(雷管置于药卷顶部)、中点起爆(雷管置于药卷轴向长度的中点位置)、孔口孔底同时起爆(两雷管分别置于药卷顶部和底部)和两点起爆(两雷管分别置于二等分炸药段的中点位置),如图6所示。

炮孔A-孔底起爆,炮孔B-孔口起爆,炮孔C-中点起爆,炮孔D-孔底孔口起爆,炮孔E-两点起爆图6 五种雷管布置方案示意图Fig. 6 Schematic diagram of five detonation methods

五种工况中,监测点均选取在地表临空面的相同位置,采集监测点的振动信号,通过傅里叶变换得到幅值谱曲线。水平径向爆破振动信号为例,图7为五种雷管布置工况下爆破振动主频和质心频率随爆心距的衰减过程,由图7可知,主频随爆心距的衰减中有突变和波动,而质心频率衰减规律更平稳。以孔底起爆为参照,利用式(2)计算孔口、中点、孔口孔底同时起爆以及两点起爆的爆破振动频率全局增量,结果列于表3。

表3 不同雷管布置工况下爆破振动频率全局增量GFINTable 3 Global increment GFIN of blasting vibration frequency under different detonation modes

图7 五种雷管布置工况下爆破振动主频fd及质心频率fc的衰减Fig. 7 Attenuation of blasting vibration main frequency fd and centroid frequency fc under five detonation modes

孔口起爆爆破振动频率衰减曲线和孔底起爆的频率衰减曲线近似重合,孔口起爆的频率全局增量GFIN非常小,由此可知这两种雷管布置工况对距爆源中远区的爆破振动频率影响差别较小。同样地,中点起爆和孔口孔底同时起爆的GFIN大小相近,且两种工况的衰减曲线近似重合,表明这两种雷管布置工况下激发爆破振动的特征频率近似相同。综合设定的五种雷管布置工况中,两点起爆的振动频率是最高的,其次是中点起爆和孔口孔底同时起爆,频率最低的为孔底起爆和孔口起爆。数值计算结果进一步证实了不同雷管布置工况下,产生的爆破振动效应不同。

3 雷管布置对振动频率的影响机理

本节从爆源叠加角度,通过分析不同工况中的爆炸荷载特征,讨论雷管布置对爆破振动频率的影响机理。

3.1 雷管布置产生的爆源叠加效应

如图6所示,无论是孔底起爆还是孔口起爆的单点起爆方式,这两种工况中起爆点引爆的是整个装药段长度Lc,爆破振动频率近似相同。中点起爆的起爆点将整个装药段等分上下两段,上下均分的两段炸药同时被引爆;孔口孔底同时起爆中两个起爆点同样是将炸药等分为两段,说明这两种工况都等效为两个同时被引爆的装药长度为Lc/2的子爆源叠加,中点起爆与孔口孔底同时起爆的爆破振动频率近似相等。两点起爆中,每个起爆点位于二等分炸药段的中点位置,两个起爆点同时引爆的装药段长度为总装药段长度的1/4,等效为四个同时起爆的装药长度为Lc/4的子爆源叠加。

因此,雷管布置对爆破振动频率的影响规律,实质是利用起爆点将炸药分为多段同时引爆,等效为多个同时被引爆的子爆源叠加。子爆源装药长度取决于起爆点位置与数量,分段越多,子爆源装药段长度越小,爆源激发振动频率越高;起爆点位置和数目不同,但其控制的子爆源装药段长度一致时,振动频率近似相等。

3.2 雷管布置对爆炸荷载的影响

基于黏弹性介质中爆破振动速度幅值谱(式5),研究雷管布置对爆破振动频率的影响规律,已知爆源几何参数、传播介质性质完全相同,仅雷管布置决定的爆炸荷载作用过程不同。爆炸荷载主要参数为荷载峰值、荷载上升时间和作用持续时间,其中影响荷载谱的是荷载上升时间[18,19]。

(5a)

其中

x=(CP/re)4+[1-(λ+2μ)/(2μ)](CP/re)2ω2

(5b)

y=[(λ+2μ)/(4μ)]2ω4

(5c)

式中:λ、μ为拉梅系数;CP为纵波速度;ν为泊松比;Qr为岩石的地质品质因子;re为弹性空腔半径;Sσ(jω)为弹性空腔内的荷载谱;ω为角频率;r为爆心距。荷载上升时间越短、上升速率越快,荷载谱中高频对应幅值比例增加,从而影响到爆破振动频谱幅值整体向高频带方向偏移,爆破振动幅值谱中高频对应幅值比例越大。

如图8所示,在数值计算的模型中沿着炮孔轴向在孔壁上布测点监测爆炸荷载作用过程,获得各测点在不同雷管布置下的荷载上升时间与上升速率,见图9。

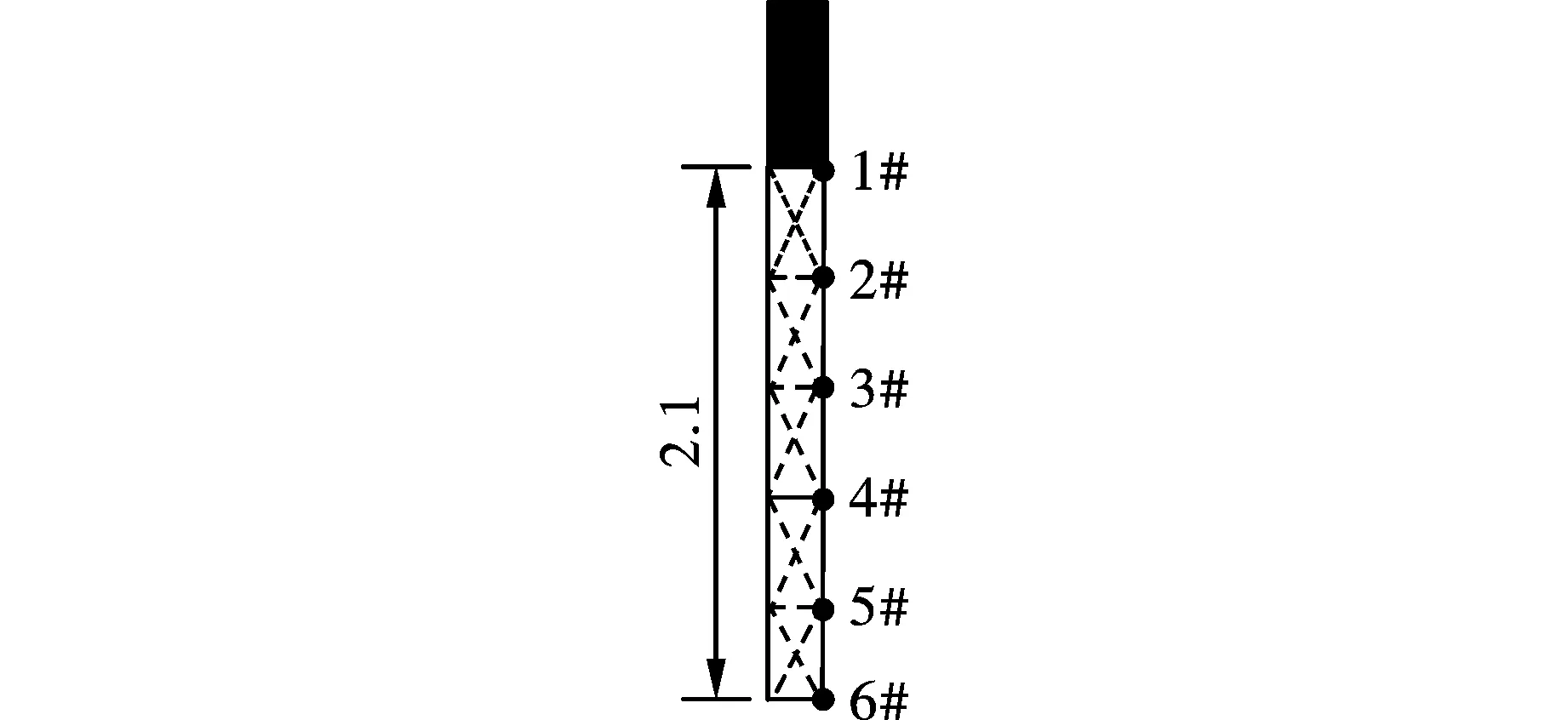
图8 炮孔壁荷载监测点(单位:m)Fig. 8 Load monitoring points on the wall of the blast hole(unit:m)

图9 不同雷管布置工况下各测点的压力上升过程Fig. 9 Pressure rise process of each measuring point under different detonation modes

由图9可知,两点起爆的荷载上升时间最短,上升速率最快,荷载谱高频成分增加,爆破振动频率最大。中点起爆和孔口孔底同时起爆的荷载上升时间和上升速率其次,因此爆破振动频率次于两点起爆;孔底起爆和孔口起爆的荷载上升时间最长,荷载上升速率最慢,爆破振动频率最小,两者荷载上升过程的爆轰压力在空间上沿炮孔轴向传播方向相反,但在时间特征上相似,因此孔口、孔底单点起爆激发的振动频率近似相等。

4 结论

通过现场试验和数值模拟相结合的方法,研究雷管布置对爆破振动频率的影响机制和作用规律,可以得出以下结论:

(1)两点起爆的爆破振动频率最高;中点起爆和孔口孔底同时起爆的振动频率近似相等,次于两点起爆的振动频率;孔底、孔口单点起爆的爆破振动频率最低。

(2)改变雷管位置或者增加起爆点数量实质上是将整个装药段分段同时引爆,等效为多个子爆源叠加,分段越多,子爆源的装药长度越小,激发爆破振动频率越高。

(3)缩短子爆源的装药段长度,可压缩孔内爆轰波传爆过程,加快爆炸荷载上升速率,进而增加了荷载谱高频成分,爆破振动频率提高。

(4)随着爆心距的增大,雷管布置对爆破振动频率的影响减弱,当爆心距达到一定值时,雷管布置方案对频率不再有影响。

电子起爆条件下雷管布置对爆破振动频率的影响研究对起爆方案的设计起到一定的指导作用。在实际工程施工中,应根据破岩效果和振动控制的侧重点不同,选择合适的起爆方案。