冲击动载下含孔洞岩石的力学特性及破裂机制*
吴 浩,凡奥奇,贾永胜,王孟来,李树建,张 斌
(1.江汉大学 爆破工程湖北省重点实验室,武汉 430056;2.中国矿业大学 矿业工程学院,徐州 221116;3.云南磷化集团有限公司 国家磷资源开发利用工程技术研究中心,昆明 650600)
近几十年来大规模、高强度、粗放式的过度开发造成地球浅部矿产资源日益枯竭,地下矿山陆续进入千米级深部开采阶段并日趋常态,特别是硬岩金属矿山。目前,国外采深超千米的硬岩矿山有112座,最深的为南非的Mponeng金矿(4350 m);国内千米以深的金属矿井有32座,最深为1600 m的崟鑫金矿[1,2]。深部资源赋存条件复杂,开采环境呈现高应力(>50 MPa)、高地温(>40℃)和高岩溶水压(>10 MPa)以及强扰动等特征,加之深部硬岩的脆性强(σc/σt>10)和储能高(>105J/m3),钻爆开挖作用下硬岩矿山巷道极易发生冒顶、片帮等破坏现象并诱发岩石动力灾害,如岩爆、突水和矿震等[3-5]。研究表明[6,7],应力是引起岩体变形和破坏的根本作用力,岩体之所以发生变形、破坏、冲击、失稳,其本质原因是开挖活动破坏了原岩应力平衡状态,造成局部区域出现应力集中,围岩破裂失稳正是在高静应力下孕育和动力扰动触发作用下发生发展的。可见,爆破扰动对巷道稳定性的影响不容忽视,研究深部硬岩巷道围岩破裂机理的动载效应意义重大。
由于硬岩巷道围岩完整性相对较好,通常可将其简化为平面应变问题来研究含孔洞岩石在不同加载方式下的破裂演化行为,继而揭示巷道破坏失稳机理。对此,国内外学者针对含孔洞岩石在各类加载方式下的力学特性和破裂演化机制开展了大量的实验和模拟研究,如研究了单轴/双轴/三轴压缩和巴西劈裂下试样的孔洞尺寸、形状、数量和排列方位、岩石均质性、温度、孔隙性等因素的影响规律,借助照相法、应变片电测法、红外热像法、声发射法、电镜实时扫描法及数字图像相关等方法有效捕捉了孔洞岩石的破裂过程,增进了对硬岩巷道破坏机理的认识[8]。考虑到硬岩巷道受机械冲击凿岩和炸药爆破的动载作用,研究人员对动载下含孔洞岩石的力学行为进行了探索,黎立云等率先分析了含直墙拱形孔洞花岗正长岩在落锤冲击破坏中的能量变化并提出了碎块飞溅速度的计算公式[9],但忽略了孔洞的边界效应。周子龙等采用数字散斑技术研究了落锤冲击下含单个和多个方形孔洞花岗岩应变演化和破坏特征[10],观察到高应变集中区有一个渐进移动和演化的过程且其形状由孔洞远处的椭圆状变为近处的狭窄长条状,试样均发生劈裂破坏。Wang等采用RFPA软件再现了竖直单向和平竖双向压缩应力波下含单个和多个圆形孔洞岩石的破裂演化过程[11]。沙润东等也采用RFPA软件探究了孔径大小、三角形应力波加载速率及幅值对含圆形孔洞岩体动态破坏特征的影响规律[12]。Qiu等采用PFC软件模拟了爆炸应力波下并行圆形双巷道的稳定性和应变能密度变化规律[13],发现应变能减小的地方安全系数较大。Zhou等还研究了含一直墙拱形孔洞和拱顶裂隙组合缺陷的绿砂岩试样在不同落锤冲击角度下的破坏模式[14],发现冲击夹角在75°以上时试样的拉伸破裂路径不受预制裂隙的影响,且动态起裂韧度随冲击角度的增大先增大后减小。事实上,爆破动载下岩体的应变率高达10~103s-1,显然采用霍普金森压杆系统(SHPB)进行强动载实验才更贴近工程实际。鉴于此,李地元等针对含圆形和椭圆形单孔洞大理岩试样分别进行了SHPB冲击加载试验[15],认为孔洞大小和形状显著影响岩石的动态强度,孔洞周边出现了平行于加载方向的拉伸裂纹、类X型初始剪切裂纹和远场裂纹,并给出了动态裂纹扩展速度的确定方法。Han等利用75 mm杆系的SHPB系统对含不同岩桥倾角和椭圆倾角的双椭圆孔绿砂岩进行了冲击加载实验并借助高速相机和扫描电镜进行裂纹识别[16],得出椭圆倾角同比岩桥倾角对试样强度的影响更显著,而对变形的影响二者则相反,并基于裂纹贯通类型归纳了试样的五种破坏模式。Tao等对动载下含不同轴比和倾角椭圆孔条状试样的断裂特征和动应力分布进行了实验和模拟研究[17],指出压缩波产生的应力集中造成岩石产生一定损伤,而试样尾端反射回来的拉伸波产生的应力集中是造成孔洞岩石破坏的主要诱因。Tao等还采用波函数展开和傅里叶变换方法推导了平面P波和柱形P波散射下圆形孔洞周边动应力分布的解析解[18]。此外,Li等利用SHPB系统对不同孔径的圆环试样进行了动态劈裂拉伸试验[19],发现动态抗拉强度随孔径增大而减小,动态下试样拉伸破裂成对称的四部分,Zhang等采用近场动力学软件获得的模拟结果也印证了这一结论[20]。
考虑到深部岩体中的巷道还同时承受地应力的静载作用[21],国内一些学者还对含孔洞岩石进行了一维动静组合加载实验,促进了对巷道围岩灾变机理的理解。Tao等和Hong分别对含侧向圆孔和椭圆孔的圆柱形花岗岩试样进行了不同静载下的动静组合加载实验[22,23],发现静载达到中等应力水平时孔壁出现岩屑弹射的岩爆现象。Li等对含圆形孔洞板状岩石也进行了类似的实验[24],发现试样动态强度在其弹性阶段随着轴向静载的增大而减小,岩石破坏模式为X形剪切破坏。Weng等对含圆形和方形孔洞的长方体试样进行了动静加载实验[25,26],指出动态裂纹起裂应力、扩展速度和破坏模式与预静载大小密切相关,圆形孔洞的起裂应力高于方形孔洞且它们随预静载的增大先增大后减小,试样破坏也由拉伸裂纹变为剪切裂纹主导,并从试样核磁共振变化特征解释了高静载下孔洞易破裂的原因。Long等采用物理实验和FLac3d数值模拟相结合的方法研究静应力和频繁爆破下圆形巷道围岩渐进破裂过程[27],指出初始应力条件控制着巷道围岩破坏区域的分布特征,爆破扰动会加剧巷道围岩的损伤深度和失稳破坏速度,垂向和水平静应力差值越大,爆破扰动造成的巷道损伤程度越大。另外,戴兵等还分别对侧面和轴向含圆孔的圆柱形花岗岩进行了循环动载及一维静载下的循环动载冲击实验[28,29],一定程度上反映了频繁爆破对巷道围岩损伤和变形破坏的扰动作用。由上综述可知,学界对于含圆形和椭圆形等常规形状孔洞试样的动态力学特性和破裂过程有了一定的了解,然而对含有复杂形状孔洞试样动力响应的研究相对较少。因此,结合工程中常见巷道断面形状对含不同形状孔洞砂岩进行了冲击加载试验,旨在探索孔洞形状和大小对试样动力特性及破坏特征的影响机理。
1 实验材料与方法
1.1 实验材料
由于沉积岩在地壳中广泛分布,本文选取极具代表性的砂岩来进行实验并委托专业的岩土公司进行试样加工。砂岩块体取自山东临沂,外观为红棕色,均质性和几何完整性较好。矿岩鉴定结果表明,这类岩石为凝灰质长石石英砂岩,具有细砂-中砂状结构和块状构造,微观结构见图1,岩石的矿物成分主要为:石英(42%,Qtz)、斜长石(35%,Pl)、方解石(9%,Cal)、沸石(8%,Kfs)、钾长石(5%,Zeo)和不透明矿物(1%)。

图1 红砂岩微观结构图Fig. 1 Microscopic structure of red sandstone
1.2 岩石物理力学参数
为了测定该类岩石的物理力学参数,我们制备了3个圆柱形试样(φ50×h100 mm)、3个巴西圆盘试样(φ50×T25 mm)和15个立方体试样(50 mm×50 mm×50 mm)及3个中心含直裂纹的半圆盘试样(SCB,semi-circular bend),利用Instron 1346岩石力学实验系统分别进行单轴压缩实验、巴西劈裂实验和变角剪切实验及三点弯曲实验。加工制作的岩石试样的不平整度和不垂直度严格满足国际岩石力学与岩石工程学会的规范要求,实验前采用HS-YS4A型岩石声波参数测试仪、游标卡尺和天平进行波速、密度等物理参数的测量,之后测定试样的单轴抗压强度、抗拉强度、弹性模量、泊松比、内聚力、内摩擦角和断裂韧度,测得岩石物理力学参数的数值见表1。

表1 红砂岩物理力学参数Table 1 Physical and mechanical parameter values of red sandstone
1.3 实验方法与仪器设备
采用中南大学的改进型SHPB系统对上述试样进行冲击加载试验,该系统将冲头设计为纺锤型,实现了半正弦波的周期加载,突破了传统的矩形波加载方法中的波形畸变和P-C振荡瓶颈,解决了岩石动力加载过程中波形弥散、应变率变化大、重复加卸载等国际难题,实现了近定常应变率下岩石动态本构参数与能耗特征的准确获取。该实验系统由氮气罐、激发装置、纺锤形冲头、入射杆、透射杆、吸收杆、动态应变仪、示波器、应变片、轴压装置(本部分不作使用)和高速摄像仪等部件组成,如图2所示。示波器为日本横河(YOKOGAWA)公司生产的DL-850E示波记录仪,动态应变仪采用北戴河电子仪器厂生产的CS-1D动态应变仪,应变片采用1/4桥接法。高速摄像仪为Photron公司生产的Fastcam Sa1.1摄像系统,最高拍摄速度为67.5 万fps(1 fps=1 ft/s=0.3048 m/s),置于试样正前方约0.5 m处,拍摄速度设置为75 000 fps,即每13.33 μs拍摄一张。为了清晰捕捉试样图像,实验过程中在摄像仪旁边架设一个大功率的补光光源。

图2 SHPB冲击加载实验系统Fig. 2 SHPB impact loading test system
霍普金森压杆实验系统原理如下[30]:实验时,通过实验系统中激发装置组合开关的系列操作,高压氮气驱动纺锤形冲头以一定速度对心撞击入射杆一端,并产生弹性应力波。弹性应力波在入射杆中以速度Ce=(Ee/ρe)1/2稳定传播,经一定时间(Le/Ce)传播至入射杆和试样交界面处时,由于两者波阻抗不同,应力波将产生透射和反射。透射波进入试样继续传播,经一定时间(Ls/Cs)传播到试样与透射杆交界面时,应力波再次产生透反射。由于岩样长度相对较小,应力波在试样中来回一次的时间只有几微秒,经过几次透反射以后,试样及两端面的应力应变基本上趋于平衡。基于动态应变仪监测的应变片的电压信号,示波器由此可以把应力波在入射杆上的入射波、反射波和透射杆上的透射波记录下来,按照应力波理论即可获得试样的应力、应变和应变率等,计算公式为
σs(t)=[σI(t)-σR(t)+σT(t)]As/(2As)
(1)
(2)

(3)
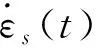
由能量守恒方程可得霍普金森压杆实验系统中入射能WI、反射能WR和透射能WT之间的相关关系及耗散能Ws的计算公式,具体[30]
(4)
(5)
(6)
Ws=WI-WR-WT
(7)
ρw=Ws/Vs
(8)
式中,ρw和Vs分别为试样的密度和体积。
2 实验方案
本次实验主要考察孔洞大小和形状(圆形、方形、马蹄形)对相同动载下孔洞试样动态变形破坏特性的影响,共制作6组试样,每组包含3个相同的试样用以进行重复实验,所有试样外观尺寸均为45 mm×20 mm×45 mm(长×高×厚),板状试样六表面均进行打磨处理以满足试样加工精度,试样中部的预制孔洞采用高压水射流技术进行精准切割。其中,G1组为用来参照的完整试样,G2~G4为三组含不同孔径的含圆形孔洞试样,G5和G6分别为含有与G3圆孔等面积的方形和马蹄形孔洞试样,试样见图3(单位:mm)。

图3 制备的岩石试样(单位:mm)Fig. 3 Prepared red sandstone specimens(unit:mm)
实验过程中,气罐的冲击气压统一设置为0.45 MPa,实验前调整实验设备使杆系各杆件相互对齐及冲头对准入射杆中心,先进行空冲实验(不放置试样)来检测冲击应力波波形。当冲击波时程曲线中入射波和透射波电压幅值相当(无明显反射波形)且连续三次空冲波形较稳定时停止空冲,随后在入射杆和透射杆上放置试样准备进行冲击加载实验。实验前在试样左右两个加载端面涂抹凡士林来消除端部摩擦效应,且放置在入射杆和透射杆正中央并夹紧,调整试样板面朝向使高速摄像机能清晰实时捕捉到试样破坏全貌。
3 实验结果与分析
3.1 半正弦波加载应力平衡性
要使SHPB测试系统记录下来的应力波形真实可靠,实验必须满足如下条件:一是SHPB杆系应严格处于一维应力状态;二是试样与杆交界面的摩擦效应很小;三是应力波在试样内经几次透反射后,试样两界面间即试样内部的应力能够很快达到平衡;前面两个条件通过实验的精心操作可轻易满足,对于第三个条件中南大学曾实践证实了圆柱形试样在半正弦波加载下的应力平衡性。对于板状试样应力是否平衡尚不清晰,我们根据试样的应力波时程曲线可绘制相应的应力波曲线,以完整试样和含圆形孔洞试样组为例,其冲击波时程曲线见图4。可见,重复实验下的应力波波形曲线吻合度较高,说明各组中试样的均质性较好,实验结果可靠度较高。

图4 试样冲击波时程曲线Fig. 4 Shock wave time-history curves of specimens
图5为完整试样和含小圆形孔洞试样组的应力波曲线。

图5 冲击载荷下板状试样应力平衡性检验Fig. 5 Stress balance validation of prismatic specimens under impact loads
以试样G1-A为例,该试样的入射波应力、反射波应力、透射波应力以及入射波和反射波应力的叠加在加载过程中的变化见图5(a)。可见,该试样的透射波应力变化曲线与入射波应力和反射波应力的叠加曲线基本上重合,尤其是在曲线的峰前时刻,这充分说明完整试样在冲击加载过程中符合应力均匀性假设。相比而言,含有一个小直径圆孔的试样G2-A的透射波应力变化曲线与入射波应力和反射波应力的叠加曲线在峰前时刻基本上也是重合的,但是透射应力波曲线的波幅小于入射波应力和反射波应力的叠加曲线的波幅,这主要是因为应力波在带有孔洞试样中传播时遇到孔洞波幅会产生衰减,其余类型孔洞试样也呈现类似的特征。显然,针对板状试样进行半正弦波下的冲击加载试验是满足应力平衡性假设条件的。
3.2 试样强度变形特性
基于动态应变仪记录的应力波电压信号可获得各组试样的动应力-应变曲线,见图6。根据动应力应变曲线可计算G1~G6组试样在一维动态冲击加载过程下的力学特性参数,见图7,包括动态抗压强度、弹性模量、峰值应变和应变率,各试样动态力学特性参数见表2。
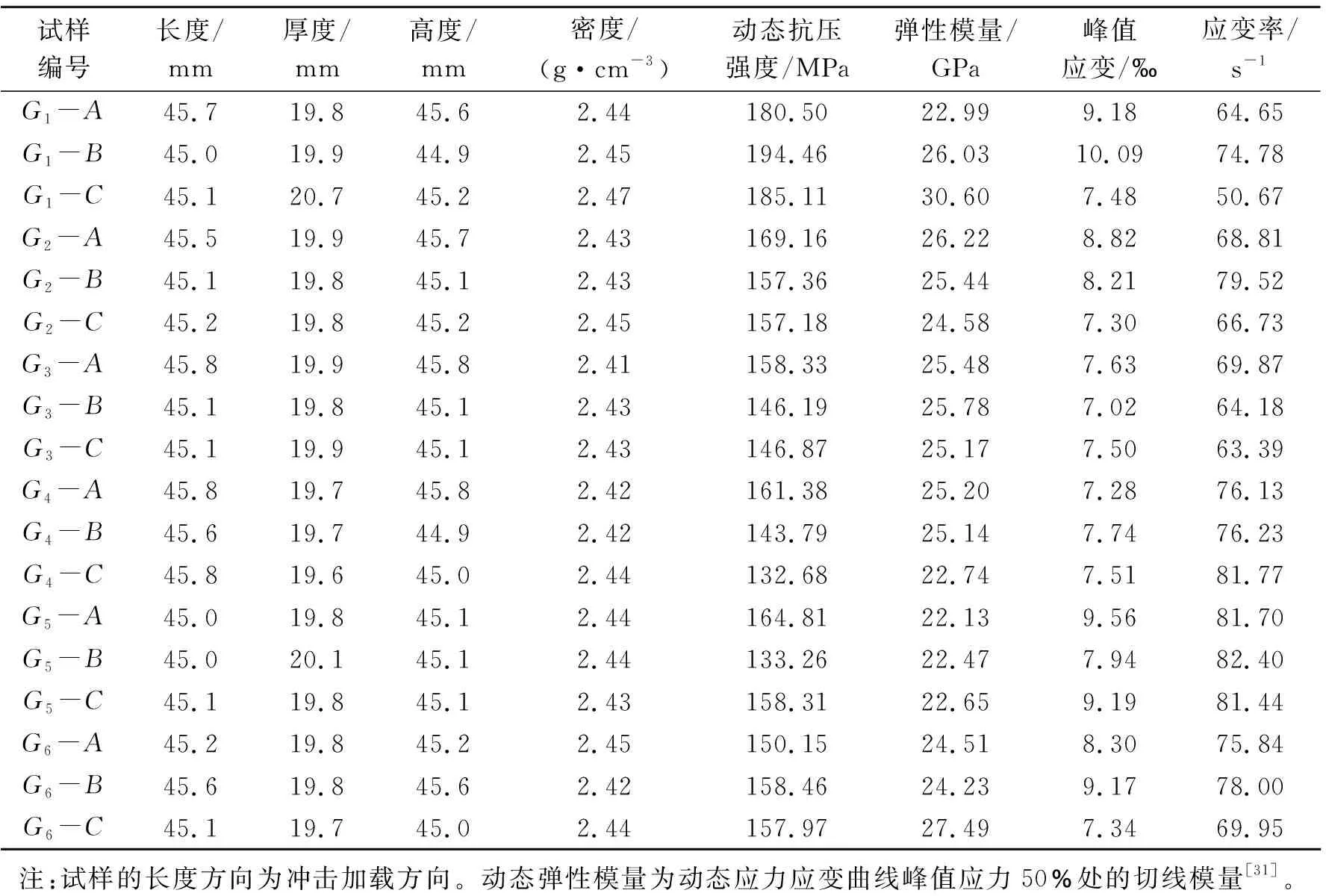
表2 冲击加载下试样动态力学特性参数Table 2 Dynamic mechanical parameter values of specimens under impact loading

图6 试样动态应力应变曲线Fig. 6 Dynamic stress-strain stress curves of specimens

图7 试样动态力学特性参数Fig. 7 Dynamic mechanical property parameters of specimens
G1组至G6组试样的平均动态抗压强度分别为:186.69 MPa、161.23 MPa、150.46 MPa、145.95 MPa、161.56 MPa和155.53 MPa。需要说明的是,为了保证实验结果可靠性,每组重复对三个试样进行实验。G5组中试样G5-B动态抗压强度为133.26 MPa,与组内其余两个试样的强度值存在很大偏差,显然该试样实验过程中可能存在气压不稳定或者冲头没有预置到初试位置,故将该试样结果予以剔除不参与平均值计算。和完整试样的强度相比,G2~G6的强度同比下降了13.64%、19.40%、21.82%、13.46%和16.69%。可见,孔洞的存在显著弱化了岩石的动态抗压强度,弱化效应不仅和孔洞大小有关,还受孔洞形状影响。
由G1~G4组试样结果可知,同一形状下孔洞尺寸越大,试样的动态强度越低,二者呈负相关关系。由G3、G5和G6组试样结果可知,相同孔洞面积下含圆形孔洞试样动态强度最小,含马蹄形孔洞试样次之,含方形孔洞试样的动态强度最大,显然孔洞形状对试样动态强度也具有显著影响,且直线型孔洞边界试样在一维动载下的承载能力高于圆弧形孔洞边界试样。同样,可得出G1~G6组试样的平均动态弹性模量分别为:26.54 GPa、25.41 GPa、25.48 GPa、24.36 GPa、22.42 GPa和24.37 GPa。可见,孔洞形状和大小对试样的动态弹性模量也有一定程度的弱化,相同形状孔洞下孔洞尺寸越大,试样弹性模量越小;不同孔洞形状中,方形孔洞试样的弹性模量同比最小,圆形孔洞的相对最大。六组试样的平均峰值应变分别为8.92‰、8.11‰、7.38‰、7.51‰、8.90‰和8.37‰,可得含孔洞试样的峰值应变均低于完整试样,但弱化效应不是很显著,基本上与孔洞半径呈线性递减的关系,且不同孔洞形状中圆形孔洞试样峰值应变最小,而方形孔洞试样峰值应变最大,与弹性模量呈现相反的变化规律。另外,可以发现0.45 MPa气压下试样的应变率范围在60~80 s-1之间,试样的应变率随孔洞半径增大基本上呈递减的变化,试样应变率形状效应中方形>马蹄形>圆形,可见试样的动态强度随着应变率的增大而增大,即呈现典型的率效应或率相关性。
3.3 试样能量转化关系
根据公式(1)~(8),可计算各试样在冲击加载过程中的入射能、反射能、透射能和耗散能。由此根据试样体积还可计算试样的能耗密度,见表3。研究表明[32],能耗密度指标可以很好地表征岩石试样的破坏特征。该指标的数值越大,表明试样内部所产生的裂隙越多,吸收的能量较大,导致试样破坏越剧烈,即破坏后的碎块尺寸越小。

表3 冲击加载下试样能量特征参数Table 3 Energy characteristic parameter values of specimens under impact loading
由表3可以看出,在相同气压下试样入射能范围在130~156 J之内,造成入射能些许差异的原因在于:①激发装置需要人工拧动阀门充放氮气,每次冲入的氮气量受氮气罐内压力及人为因素可能有些许差异;②每次完成冲击试验后,冲头需要人工采用软铁丝捣入初始位置,受人为因素影响,冲头的初始位置可能有些不同,以致冲头的撞击速度有差异。耗散能主要用于驱动试样内部裂纹的萌生、扩展和贯通,破坏剧烈程度体现在能耗密度上。六组试样的平均能耗密度分别为:1.64 J/cm3、1.71 J/cm3、1.73 J/cm3、1.81 J/cm3、1.67 J/cm3和1.94 J/cm3。可见,完整试样单位体积内吸收的能量最小,相同形状下孔洞尺寸越大吸收的能量越大,不同形状孔洞试样中马蹄形孔洞试样>圆形孔洞试样>方形孔洞试样,表明马蹄形孔洞试样破坏过程最剧烈,完整试样破坏程度最不显著。
为了进一步分析冲击加载下孔洞岩石的破坏情况,采用分形几何理论对岩石破碎块度进行分析。实验前,将一个方形铁箱子(前表面和上表面开口以提供摄像空间)放置在试样下方的SHPB基座上来收集破碎岩屑。实验结束后采用筛径为5、10、15、20和40 mm的标准筛进行筛分,将破碎岩石分为0~5 mm、5~10 mm、10~15 mm、15~20 mm和20~40 mm共5个等级,各试样每一粒级的累计岩石碎块重量见表4。已有文献表明[33],岩石破碎块度分布方程为
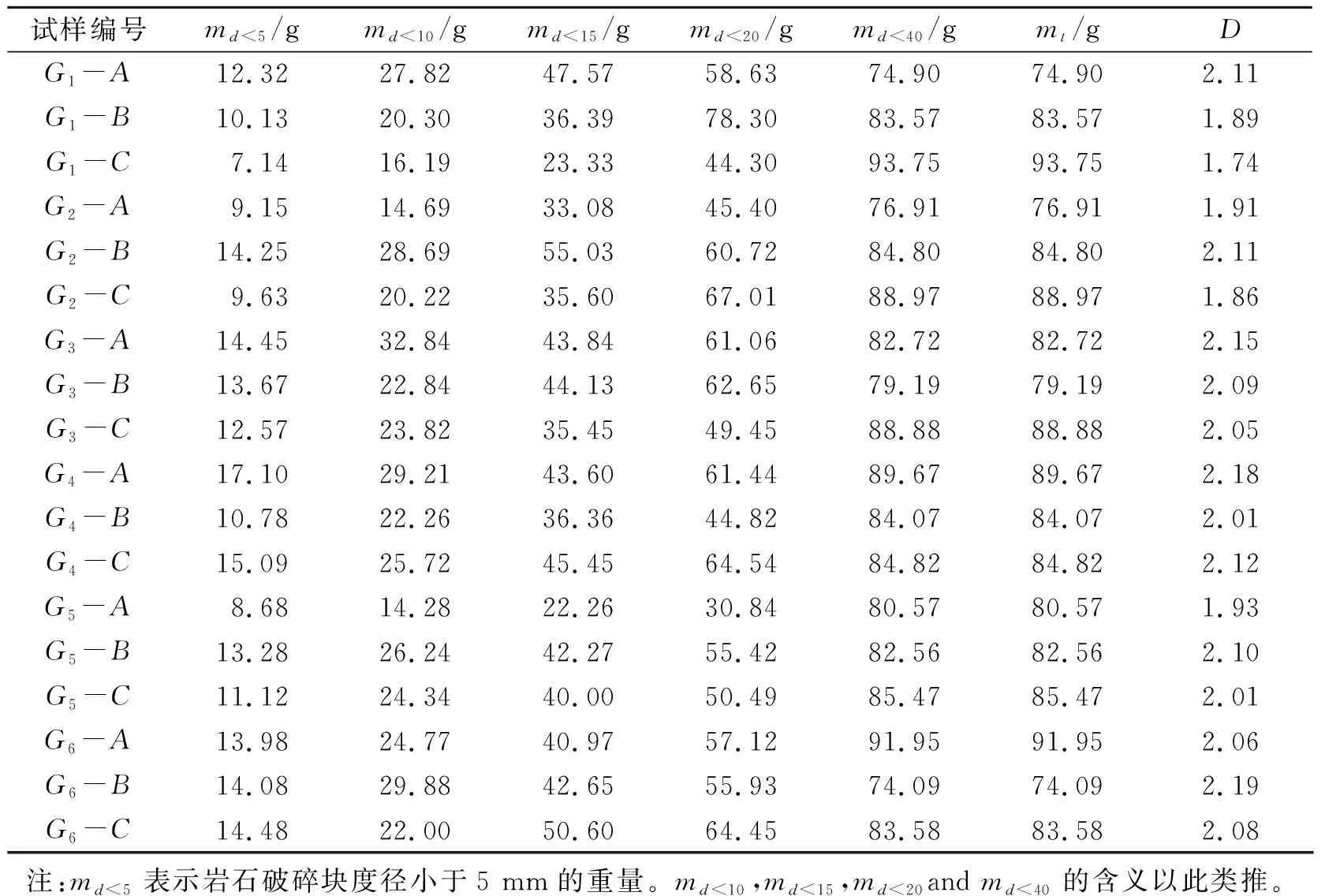
表4 冲击加载下试样分级质量及分形维数Table 4 Fractal dimensions and grading weight of specimen fragment under impact loading
(9)
式中:d为碎块粒度;dm为最大粒径,40 mm;md为尺寸小于d的试样碎块累计质量;mt为碎块总质量;D为试样碎块的分形维数。
对式(9)两边取对数可得(3-D)为lg(md/mt)-lg(d/dm)拟合直线的斜率,因此可通过多点线性拟合求得D的值。试样碎块分级质量统计及拟合结果分别见表4、图8。拟合分析表明:各试样拟合直线的相关系数平方均大于0.92,可见各试样的拟合度较好。

图8 试样分形维数线性拟合曲线Fig. 8 Linear fitting curves of fractal dimension of specimens
上述6组的平均分形维数分别为1.91、1.96、2.09、2.10、2.01和2.11。可见,完整试样的分形维数最小,孔洞试样的分形维数同比较大,表明孔洞试样的破碎程度比完整试样要剧烈。相同孔洞形状下,小圆形孔洞试样的分形维数最小,大圆形孔洞试样的分形维数最大,充分证实了大尺寸孔洞试样的破碎块度要小;不同孔洞形状下,马蹄形孔洞试样的分形维数最大,圆形孔洞试样和方形孔洞试样地相差不大,各试样的分形维数与能耗密度变化趋势基本一致。总的来说,分形维数越大,试样破碎程度越剧烈,块度越小。可见,采用分形维数表征的试样破碎块度和能耗密度反映的试样破碎程度得出的结果基本相吻合。
3.4 试样动态破坏模式
根据高速摄像仪抓拍的系列照片,可获得各试样内部裂纹的动态扩展过程。表5给出了每组中的代表性试样在不同时刻下的破坏形态。由表可见,完整试样(G1-B)在加载过程中先在左上角出现一拉伸裂纹,随着时间的发展它开始向右上角扩展。传播期间,试样左端部中间和左下角也陆续出现了一条拉伸裂纹。受端部效应,左下角的拉伸裂纹传播方向并非完全平行于加载方向。相比之下,中间的拉伸裂纹基本上沿加载方向直线传播,直至传播到试样右端。由此可知,完整试样的破坏模式为劈裂拉伸破坏。

表5 冲击加载下试样破坏过程Table 5 Failure process of specimens under impact loading
对于含有小直径孔洞的试样,随着动载的施加,孔洞的上下孔壁受瞬态压应力集中作用的影响,孔壁产生剥落弹射。然后试样右上角和左下角分别产生一个剪切裂纹并朝孔洞传播直至贯通。同时,在试样左端左上角和左下角还有两条拉伸裂纹,基本上沿加载方向传播直至扩展到试样右端面。由此可见,小直径圆孔的破坏模式为拉剪破坏。含有中等直径圆孔的试样在加载过程中内部裂纹的扩展过程和含有小直径孔洞试样的基本相同,试样最后也发生拉剪破坏。对于含有较大直径孔洞的试样,在冲击加载过程中,孔洞上下侧壁受动态压应力集中也产生剥落弹射,紧接着试样四个拐角同时产生剪切裂纹,并朝孔洞传播直至贯通产生破坏,同时在孔洞下方也出现有一水平传播的拉伸裂纹,试样的破坏模式同样属于拉剪破坏。虽然在试样的右端面在最后时刻看到有一个水平方向的短小拉伸裂纹,但是它并未与孔洞产生贯通,对试样的破坏不起主导作用。
对于含方形和马蹄形孔洞的试样,其在冲击加载下的破坏机理是相同的,即加载初期孔洞的顶部和底部受压应力集中作用出现弹射型剥落,随后在试样对角线上有剪切裂纹陆续出现,紧接着有一条近似水平的拉伸裂纹出现在孔洞下部并逐渐从试样一端扩展至另一端。由上表可知,两类试样的破坏模式均为拉剪破坏,与圆形孔洞试样在动载下的破坏模式一致。通过高速摄像仪拍摄的照片我们还发现,D6-B试样的破坏过程同比其他试样剧烈,产生的碎片较多。这主要是因为其能耗密度最大,以致试样的破碎块度较小。
4 结论
采用50 mm杆径的改进型霍普金森压杆实验系统对中等硬度的系列含孔洞板状红砂岩进行了冲击加载实验,分析了孔洞尺寸大小和形状对岩石动态力学特性参数和破坏机理的影响规律,得出结论如下:
(1)岩石试样单轴抗压强度为99.32 MPa,弹性模量24.43 GPa,泊松比为0.26,内摩擦角为40.43°,断裂韧度为0.59 MPa·m1/2,岩石峰后阶段较短,呈现典型的硬岩脆性破裂特征。
(2)完整板状岩石和含孔洞板状岩石在半正弦波冲击加载过程中入射波和反射波的叠加曲线和透射波曲线在峰前基本重合,证实了板状试样用以开展半正弦波下的霍普金森压杆实验能够满足应力均匀性假设条件。
(3)孔洞尺寸和形状对岩石动态力学特性参数具有显著弱化作用。随着孔洞尺寸的增大,岩石动态抗压强度、弹性模量和峰值应变基本线性递减。不同孔洞形状试样中,动态抗压强度和峰值应变:方形孔洞试样>马蹄形孔洞试样>圆形孔洞试样,弹性模量则呈现相反的结论。岩石应变率在60~80 s-1之间,组内试样的动态抗压强度还呈现出率相关性。
(4)完整板状岩石破坏模式为劈裂拉伸破坏,含孔洞板状岩石均发生拉剪破坏。圆形孔洞试样能耗密度与分形维数随着孔洞尺寸增大而增大;不同形状孔洞试样中,马蹄形孔洞岩石试样的能耗密度和分形维数最大,其破坏过程最剧烈,含圆形孔洞和方形孔洞试样的破碎块度相差不大。

