钢制流道泵站肋板局部加高对结构振动的影响

赵路静，李 灿，张燎军，张汉云，张 冬

(1.浙江省水利水电勘测设计院有限责任公司，浙江 杭州 310002；2.河海大学水利水电学院，江苏 南京 210024)

0 引 言

在泵站运行过程中，机组和泵房的振动是最常见且需予以高度重视的问题。剧烈的振动将直接影响机组的安全可靠运行，极大的缩短机组的检修周期及使用寿命，严重时，甚至还会引起整个泵房结构的振动，造成被迫停机等严重后果[1]。

某大型输水工程拟采用钢制流道的立式轴流泵站，旨在减少施工流程，降低施工难度且提高流道的强度、刚度和稳定性。但由于该方案在国内运用较少，并且钢制流道为薄壁型结构，在运行过程中易发生振动，需要通过论证和检验来明确设计是否科学合理[2]。本文以某大型钢制流道立式轴流泵站项目为依托，建立泵站混凝土结构-钢制流道-流体的流固耦合有限元模型，分析钢制流道轴流泵站应力、变形及振动响应，针对局部振动剧烈问题，提出了加强该部位肋板厚度的解决思路，重点分析了肋板局部加高对结构静动力响应的影响。

1 计算理论依据

1.1 连续性方程和N-S方程

泵站运行过程中，其内部的流动规律可用连续性方程和N-S方程予以表达[3]，即

(1)

式中，ρ为流体密度；μ为流体的动力粘滞系数；ui，uj(i=1，2，3；j=1，2，3)为流体的速度分量；p为压力；ρFi为质量力。

1.2 流固耦合界面条件

在流固耦合面上，应当满足动力和运动边界条件[4]，即

(2)

式中，df为流固耦合面上流体的位移；ds为流固耦合面上固体的位移；τf为流固耦合面上流体的应力；τs为流固耦合面上固体的应力；n为流固耦合面上的法向向量。

由运动边界条件求得流体的速度边界条件为

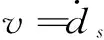
(3)

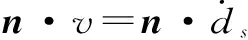
(4)

对泵站进行水力机械全流道三维非定常湍流计算，模拟预测所得结果更接近事实。本文应用全三维非定常湍流的真实时间法，计算钢制流道立式轴流泵站内的静动干扰[5-8]。

2 计算模型及主要参数

2.1 结构计算网格

本文运用大型有限元软件ADINA，建立泵站混凝土结构-钢制流道-流体的流固耦合有限元模型。该模型真实反映了泵站的设计构造，建立了进水口、楼板、墙、柱、机墩、钢制流道、混凝土支座及流道外壁的肋板等结构。整体模型共划分单元74 310个，节点总数85 723个。图1为该泵站的整体有限元模型。在泵站的底部、底部与下游墙体交接处、垂直流向的墙体处施加法向链杆约束。该模型的坐标系统取为：以叶轮中心点所在位置为坐标轴原点，Y轴沿水流方向水平指向站上，X轴为垂直水流方向，Z轴竖直向上。图2～4分别为钢制流道、混凝土—钢制流道及水体的有限元网格。

图1 泵站整体有限元模型

图2 钢制流道有限元网格(含肋板)

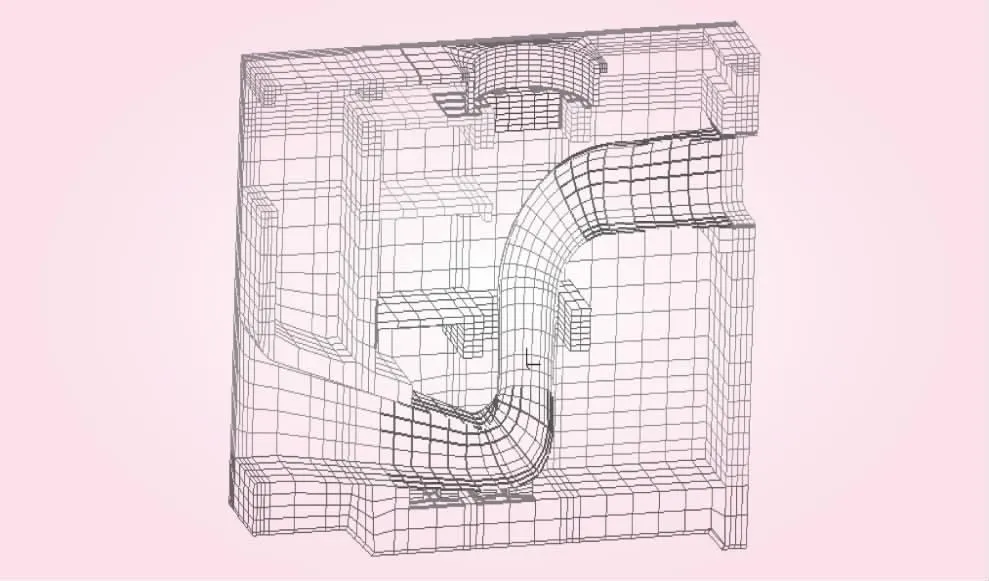
图3 混凝土-钢制流道有限元网格(单流道)

图4 水体有限元网格

为模拟振动传递路径并进行合理的泵房结构-钢制流道振动分析，将轴流泵、泵轴、机架进行有限元建模。其中，整体轴流泵及其各部件有限元网格划分如图5所示，共划分网格17 824个。泵轴与上部机架通过设置接触单元建立联系，由上部机架承受叶轮及泵轴重量等垂直荷载。泵站在正常运行时，通过泵轴的旋转带动整个叶轮旋转，其网格划分如图6、7所示，泵轴和机架共划分三维实体单元2 832个。在机架与机墩之间通过竖向约束方程的建立，模拟机墩对机架的支撑作用。泵站整体模型剖分如图8所示。

图5 整体泵网格

图6 叶轮及主轴

图7 机架及主轴

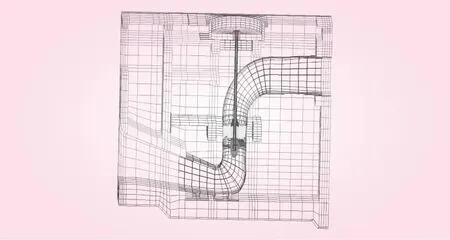
图8 结构-钢制流道-泵整体网格(单流道)

2.2 全流道流体计算网格

泵站全流道包括进水流道、叶轮、固定导叶、出水流道。在本文建立的模型中，将全流道流体划分为4个子区域：第1区域为进水流道，第2区域为叶轮转动区域流体，第3区域为固定导叶内流体，第4区域为出水流道。全流道网格划分如图9所示。模型中，采用六面体单元(部分采用五面体单元)对流体域进行划分。全部计算区域单元总数为45 386，节点有51 553个。

图9 全流道流体网格

流道各部分参数为固定导叶7片，叶片数为4片，转轮直径1.95 m，转速n=214.5 r/min，即转频f=3.575 Hz。模型其他主要材料参数见表1。

表1 材料参数

3 肋板局部加高后泵站结构的静力分析

经初步计算发现，该钢制流道立式轴流泵站3个机组的混凝土泵房结构间的影响不明显，故为了重点研究钢制流道的振动特性，并且降低计算难度和运算时间，本文选择单机组段进行详细的分析和研究。分析计算成果可得，该泵站混凝土结构的振动远小于钢制流道的振动，不是强度控制的主要因素。为着重分析研究在泵站机组运行时钢制流道的振动响应，分别在钢制流道的不同部位设置测点，具体位置如图10所示。

图10 钢制流道测点布置

在泵站停机时，钢制流道进口附近的顶面(图10中关键点1)，在静水压力作用下竖直方向的位移较大，达到11.981 mm。针对这一现象，拟将钢制流道关键点1附近的3圈环向肋由10 mm加高到15 mm，加高肋位置如图11中3根加粗环向肋所示。

图11 加高肋位置示意

表2、3列出了加高肋板方案下结构各方向的最大位移、最大应力值，并与原设计方案下结构各方向的最大位移、最大应力值进行了对比。

表2 泵站停机工况钢制流道结构最大位移值

由表2可知，钢制流道X方向最大位移为1.017 mm，最小位移为-1.015 mm，分别发生在钢制流道上游转弯处附近的侧向流道处，基本呈对称分布；Y方向最大位移为2.965 mm，发生在钢制流道叶轮高程附近，位于近下游面；Z方向最大位移为9.431mm，位于近钢制流道与混凝土流道连接处的顶面。表2中列出了加高肋后，钢制流道各方向最大位移减小的百分比，可知，加高环向肋后钢制流道各个方向最大位移均有明显减小。泵站在停机工况下，钢制流道纵向最大拉应力发生在钢制流道进口附近的流道上方，稍偏向X轴正方向；最大压应力发生在叶轮高程附近，且靠近下游侧。横向最大拉应力位于叶轮高程附近，偏向X轴负方向；最大压应力位于流道偏向上游侧转弯方向的上部。竖向最大拉应力位于钢制流道进口附近的侧面，且偏向X轴正方向；最大压应力位于60°弯管处，偏向X轴正方向。第一主应力的最大值位于叶轮高程附近，偏向X轴正方向；第三主应力的最大值位于流道偏向上游侧转弯方向的侧面，偏向X轴正方向。表3中列出了加高肋后，最大应力减小的百分比，可知，加高肋后，钢制流道各方向应力值亦均有明显减小。

表3 肋板加高后泵站停机工况钢制流道结构最大应力值

4 肋板局部加高后泵站结构动力响应分析

4.1 边界及荷载条件

对建立的流固耦合有限元模型，设置时间步长为0.01 s，共计算5 000步。流体边界条件的设置具体如下：

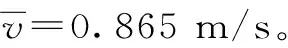
参考资料表明[9]，闸泵结构在流激振动作用下，流道内的脉动压力最大频率约达到1.0倍的机组转动频率，压力不均匀度小余16%。文中选取水体流速脉动频率等于机组转频，脉动幅值为流速10%的简谐脉动水流模拟全流道内的水体。

流道的出口边界条件设置为自由出流[10-11]。在固体、流体的交界面上，均设置流固耦合边界条件，参考压力点取水泵的中心线。

4.2 肋板局部加高后振动响应分析

肋板加高后，钢制流道各个关键测点振动位移、应力幅值如表4、5所示。由表4可知，肋板加高后，钢制流道各测点各方向的振动位移整体呈现降低趋势，部分点的位移有增大趋势，但增幅不明显，且由于除测点1外，其他测点静力计算所得位移值较小，增加的振幅对其安全运行影响不大。由表5可知，肋板加高后，钢制流道各测点各方向的振动应力整体呈现降低趋势，部分点的某一方向应力有增大趋势，但增幅不明显。

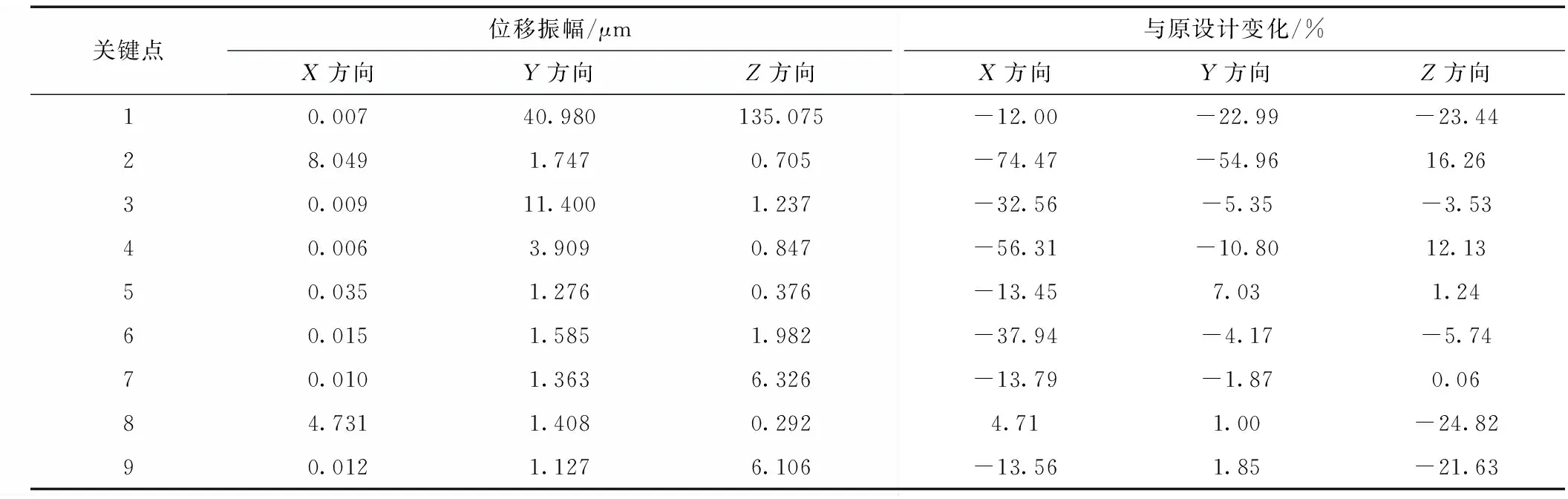
表4 肋板加高后正常运行工况钢制流道各测点振动位移幅值

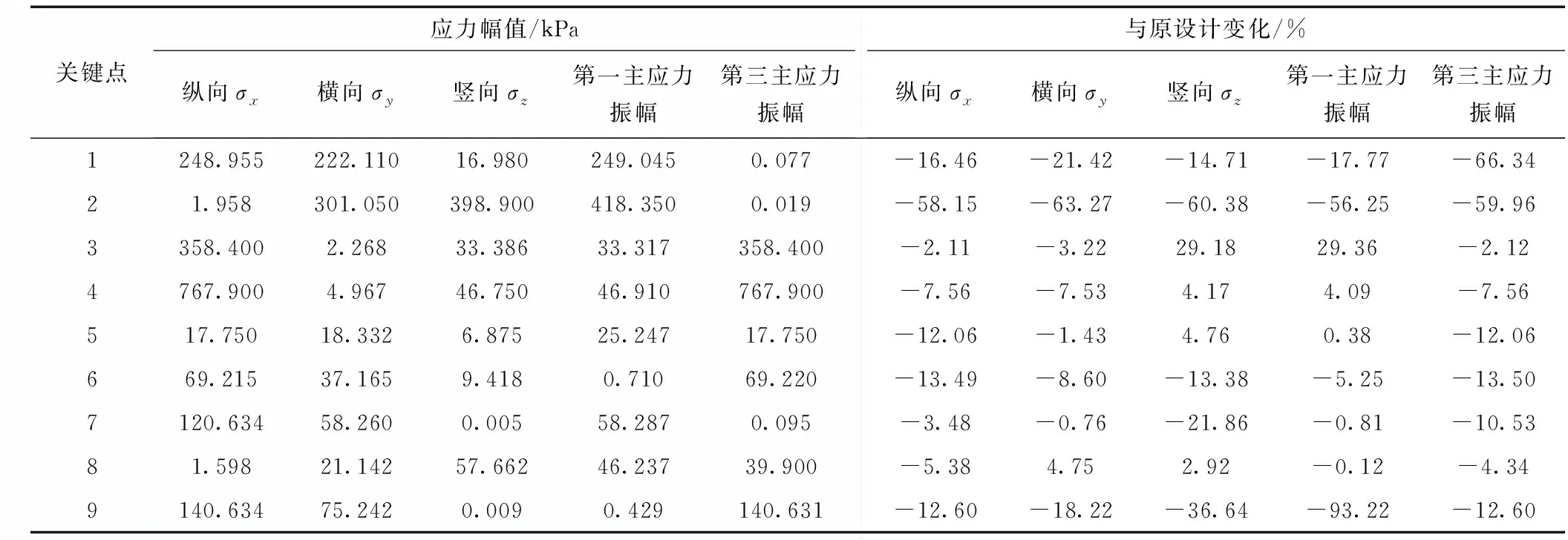
表5 肋板加高后正常运行工况钢制流道各测点振动应力幅值

5 结 论

本文结合某钢制流道立式轴流泵站工程，运用有限元软件ADINA对该泵站的振动传递路径进行了仿真模拟，建立泵站混凝土结构-钢制流道-流体的三维流固耦合有限元模型，分析了钢制流道关键测点的应力、变形和振动响应，针对局部振动剧烈问题，提出了加强该部位肋板厚度的解决思路，分析表明，加高钢制流道和混凝土流道连接处顶部的三根肋板后，泵站整体静位移、动位移、应力等均有所降低(局部有增大趋势，但增幅不明显)，效果较为显著。通过肋板加高达到降低振动响应的方案对泵站钢制流道的设计和应用具有一定的参考价值。