融合时间感知与兴趣偏好的推荐模型研究
唐 潘,汪学明
1.贵州大学 公共大数据国家重点实验室,贵阳 550025
2.贵州大学 计算机科学与技术学院,贵阳 550025
随着信息技术的快速发展,人们从海量数据中获取目标信息变得十分困难,个性化推荐系统[1-2]为此提供了一个良好的解决方案,可以帮助用户快速地获取到目标信息,减少用户的时间成本。其核心是推荐模型对用户的交互行为进行分析,精准刻画用户的画像,进而实现向用户提供感兴趣的内容。
传统协同过滤推荐[3]可以分为基于用户的协同过滤推荐[4]和基于项目的协同过滤推荐[5],这些方法在推荐系统领域获得了广泛的研究和应用,但这类算法忽略了用户兴趣偏好是一个动态变化的过程[6],以及在数据稀疏时存在不能提供良好的推荐性能的问题[7]。
当前,随着深度学习的发展,基于深度学习的推荐模型成为研究的热点,与传统的推荐方法相比,基于深度学习的推荐模型具有更强的深层表达能力,可以学习到更多深层的语义信息,从而解决数据稀疏以及兴趣爱好特征提取不足等问题[8]。He等人[9]将神经网络与协同过滤推荐进行结合提出神经协同过滤推荐模型(neural collaborative filtering,NCF),采用多层感知机网络学习用户和项目之间的交互关系,从而捕捉高阶非线性特征。随着循环神经网络[10](recurrent neural network,RNN)、卷积神经网络(convolutional neural network,CNN)和注意力机制[11]的兴起,在许多任务中具有较好的表现,同时在推荐任务中也取得了较好的成绩。然而RNN网络在决策时需要过去所有的隐藏状态,无法进行并行计算,存在梯度爆炸或消失等问题,以及在基于注意力机制的模型中只考虑行为序列的相对位置信息具有一定的局限性。
为了解决上述问题,本文提出了融合时间感知与兴趣偏好的推荐模型(recommendation model based on time aware and interest preference,TAIP),该模型将用户的交互时间间隔信息融入到序列嵌入矩阵中,利用多尺度时序卷积网络和Transformer编码器挖掘用户细粒度的长短期兴趣偏好,并从整体上融合长短期兴趣偏好,从而实现更好的推荐效果。
1 相关工作
序列推荐模型的核心是从用户的行为序列中构建用户随时间变化的兴趣偏好,再基于兴趣偏好提供个性化的推荐内容。在早期的序列推荐方法研究中,典型的代表是基于马尔可夫链[12]的推荐方法,该方法从用户的行为序列中学习下一个状态,得到用户点击项目i+1 的概率,但该方法只能关注到局部信息,无法从整体构建用户的兴趣爱好,对推荐模型性能的提升有限。
近年来,由于深度学习技术具有更强的深层表达能力,基于深度学习的序列推荐研究得到了较好的发展。循环神经网络具有能处理序列数据的特点,在序列推荐中应用比较广泛。Feltus等人[13]利用循环神经网络对用户的行为序列进行学习,取得了不错的效果。Sun等人[14]将用户的行为序列送入到长短期记忆网络(long shortterm memory,LSTM)中进行训练,得到隐藏空间中不同时期的特征信息,再融合不同时期的特征从而得到了静态的兴趣爱好,也取得了不错的成绩。Tang等人[15]基于卷积神经网络提出了Caser 模型,将用户行为序列嵌入矩阵分别使用水平卷积核和垂直卷积核并行获取序列中的兴趣偏好信息,提高了内存的使用效率。Chen等人[16]基于时序卷积网络(temporal convolutional network,TCN)提出了MPM模型,在模型中使用时序卷积网络提取了用户行为序列中的短期爱好,并训练了一个行为检测器判断兴趣爱好对目标项目的影响,取得了不错的效果。但这些基于RNN 和CNN 的推荐方法在处理长距离依赖关系时,会出现梯度爆炸或者梯度消失问题,以及不具有并行计算能力的问题。Chen 等人[17]提出BST模型,采用可以并行计算的多头注意力机制,自适应计算序列中每个项目的权重系数,在多个数据集上取得了较好的成绩。
上述模型虽然可以在一定程度上获取用户的兴趣偏好,但仅考虑行为序列的相对位置信息存在一定局限性,因为用户的兴趣偏好不是一成不变的,而是会随着时间的变化而动态变化。为了引入用户交互的时间信息,Li等人[18]将用户序列中的时间间隔信息作为重要的因子,设计了一个时间间隔感知的注意力机制去学习各个项目的时间间隔权重,再进行推荐,取得了优异的成绩。但通常认为距离当前时刻较远的项目对用户兴趣偏好的影响较小,反之,较大,因此,如何准确获取用户的时间间隔信息是至关重要的。
在本文提出的TAIP模型中,首先,在嵌入层通过时间间隔函数和时间位置解码器为每名用户提供个性化的时间间隔信息,从而增强序列嵌入矩阵的位置信息表示;其次,采用多尺度时序卷积增大感受野,捕获更多细粒度的序列关系,并通过通道和空间注意力机制得到用户细粒度的短期兴趣偏好;同时,采用Transformer编码器从整体上提取用户的兴趣偏好,并通过注意力网络探索待推荐项目与兴趣偏好之间的关系,从而获取用户的长期兴趣偏好特征;最后,综合考虑用户的长短期兴趣偏好进行个性化推荐。
2 融合时间感知与兴趣偏好的推荐模型
本文提出的TAIP模型,整体结构主要由嵌入层、多尺度时序卷积层、Transformer层和全连接输出层四个部分组成,如图1所示。通过嵌入层可以得到用户和项目在隐藏空间中的初始嵌入向量,同时在用户序列嵌入矩阵中引入时间位置信息加强序列的特征表示;多尺度时序卷积层采用多个尺度卷积操作获取不同时期的兴趣偏好,再利用通道和空间注意力机制对不同时期的兴趣偏好进行细粒度的特征提取,获得用户的短期兴趣偏好;Transformer层采用Transformer编码器建模用户的兴趣偏好,并通过注意力网络探索目标项目与兴趣偏好之间的关系,从而得到用户的长期兴趣偏好;最后全连接输出层融合用户所有相关特征,获得目标项目的概率分布。
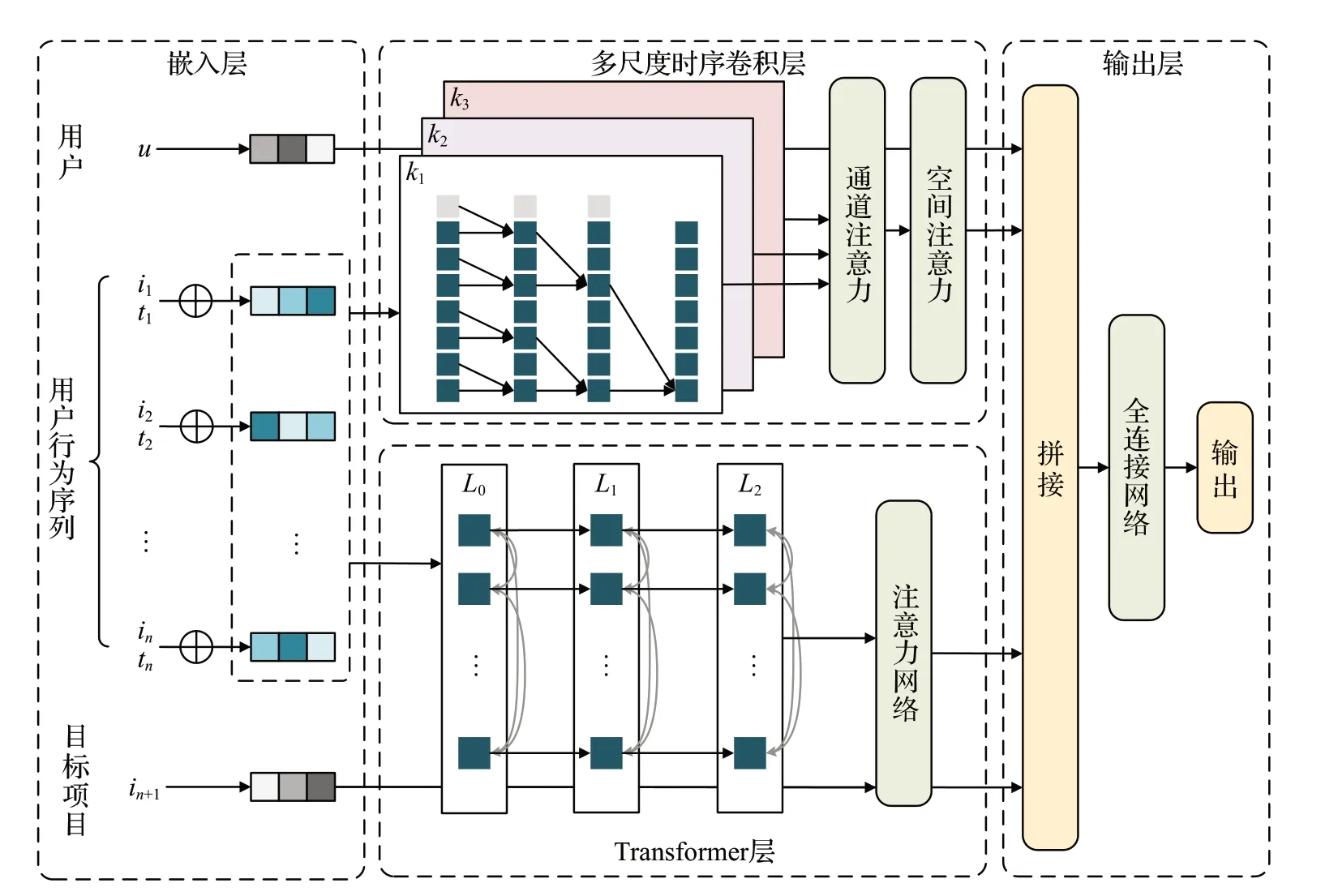
图1 TAIP模型整体结构Fig.1 Overall structure of TAIP model
2.1 嵌入层
嵌入层将用户集合U和项目集合I分别映射为嵌入矩阵EU和EI,其中嵌入矩阵EU的第u行eu,表示用户u的嵌入向量;嵌入矩阵EI的第i行ei,表示项目i的嵌入向量。对于用户u的行为序列,本文使用su=(i1,i2,…,in)表示,并通过嵌入层将su映射为序列嵌入矩阵Bu=[e1,e2,…,en],其中n表示用户行为序列的长度,en表示用户行为序列中第n个项目的嵌入向量。
由于TAIP 模型中使用的多尺度时序卷积网络和Transformer 编码器不能捕捉用户行为序列中的相对位置信息,因此本文在嵌入层中引入时间位置信息加强模型对位置信息的学习。对于每名用户具有不同的时间间隔信息,以及不同时期的项目对当前推荐任务的重要程度也不同,所以在TAIP 模型中采用时间间隔编码的方式获取时间信息。首先,将用户行为序列的交互时间定义为Tu=(t1,t2,…,tn),则在t时刻可以计算交互时间距离当前时刻的间隔;其次,为了表示距离t时刻较远的项目具有较小的影响力,本文设计的时间间隔函数如式(1)所示,该函数可以将较远的项目赋予较小的权值:
其中,t表示当前时刻;ti表示第i个项目的交互时间;表示用户行为序列间隔时间的平均值。得到用户的时间间隔后,再通过时间位置解码器得到用户的时间位置矩阵T,公式如下:
最后,将用户的时间位置矩阵T融入到嵌入矩阵Bu中,得到带有时间位置信息的序列嵌入矩阵=Bu+T。
2.2 多尺度时序卷积层
在时序卷积网络中,膨胀因果卷积网络保证了t时刻的输出仅与t时刻之前的输入有关,使得网络无法关注到未来时刻的项目,因此在推荐任务中可以理解为根据用户的行为序列中确定下一时刻点击的项目。
为了从用户行为序列中获取用户细粒度的短期兴趣偏好,本文使用多尺度时序卷积网络对用户行为序列的嵌入矩阵进行建模学习,获取用户各时刻的兴趣偏好。
在传统的时序卷积网络中只使用单一的卷积模板,导致一次时序卷积只能观察到特定维度的特征信息,需要加深卷积次数或增大扩张系数才能观察到全局特征。为了改善不足,Ma 等人[19]采用密集连接的方式在时间尺度上获取相应的特征,从而提高时序卷积网络的性能,但在该网络中存在以下问题:单次卷积操作仅在一个尺度上进行运算,所有尺度不能并行运算;得到不同尺度的特征信息后,使用单一的加和方式进行特征融合;以及采用密集连接在深层时序卷积网络中引入了大量的参数和冗余信息,导致模型容易出现过拟合现象。
为了解决这些问题,本文在多尺度时序卷积网络中,采用不同大小的卷积核对嵌入矩阵进行并行卷积操作,以及引入不同的膨胀系数,增加卷积操作的感受野,从而得到不同尺度的特性信息,最后再利用通道和空间注意力机制计算不同尺度特征之间的重要程度进行特征融合,从而增强特征的表示。多尺度时序卷积层如图2所示。
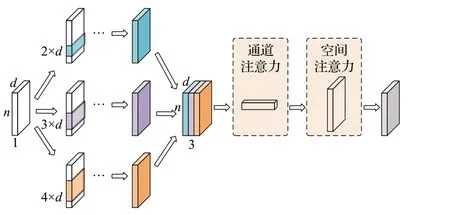
图2 多尺度时序卷积网络层结构Fig.2 Multi-scale TCN structure
其中,k为卷积核大小;ε为膨胀系数,通常设置为2i;(k-1)×ε为Padding填充值;表示l层第j个卷积的权重参数;表示l层第j个卷积的偏置;σ(⋅)表示激活函数;∗表示膨胀因果卷积运算,运算过程可以表示为。同时为了缓解单尺度中因时序卷积网络叠加所导致的梯度消失和过拟合问题,在时序卷积中引入了残差连接方式将前一层的特征信息加入到下一层。
多尺度时序卷积网络由三个并行的时序卷积网络组成,卷积核大小分别设置为k1=2,k2=3,k3=4,其中较大的卷积核,可以捕获序列中较长的特征,从而提取出较大尺度的语义信息;较小的卷积核,更容易关注到较短的序列特征,从而提取出较小尺度的语义信息。在多尺度卷积网络完成卷积操作后,分别将输出在通道维度上进行拼接得到特征,并利用通道和空间注意力从通道和空间维度对特征F进行融合,从而得到用户的兴趣偏好。其中通道注意力分别对特征F进行全局平均和最大池化,再通过激活函数得到注意力权重矩阵,最后将注意力权重矩阵与特征F相乘得到通道注意力的输出F′,公式如下:
其中,fc(⋅)表示通道注意力操作;AP(⋅)表示全局平均池化;MP(⋅)表示全局最大池化;⊗表示元素乘法。
在空间注意力中,首先对F′进行了全局平均和最大池化;其次,使用一层卷积网络生成空间注意力权重矩阵fs(F′),表示不同通道上的权重系数,最后,与输入特征相乘并在通道上进行加和,从而得到用户的短期兴趣爱好表示,公式如下:
其中,fs(⋅)表示空间注意力操作;k1×1表示卷积核大小;⊙表示卷积运算。
2.3 Transformer层
用户的行为序列不仅可以学习用户的短期兴趣偏好,还可以根据用户短期兴趣偏好学习用户的长期兴趣偏好。因此,模型中Transformer层采用双向Transformer编码器建模学习用户的行为序列,使得模型在任何时刻都能观察到行为序列中的所有项目,从而学习到用户的长期兴趣偏好。
Transformer 层主要由多个叠加的Encoder-block 和注意力网络构成。其中每个Encoder-block的结构如图3所示,主要包括多头注意力机制、前馈神经网络、残差连接和归一化层。
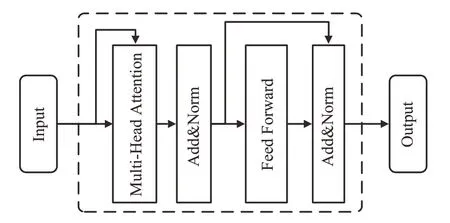
图3 Encoder-block结构Fig.3 Encoder-block structure
多头注意力机制可以在不同的隐藏空间中对用户行为序列的内部关系进行学习,从而捕捉到更丰富的特征。首先,将带有时间位置信息的嵌入矩阵通过线性变换得到Q、K、V矩阵,并通过公式(6)计算第h个子空间中的输出:
其中,Att(⋅)表示一般注意力机制;softmax(⋅)表示激活函数;Qh、Kh、Vh表示第h个子空间的嵌入矩阵;表示缩放因子,可以避免内积过大导致的梯度爆炸;T 表示矩阵的转置。
在得到各子空间的输出后,将输出进行拼接,并通过参数wH进行特征变换得到多头注意力机制的输出,公式如下:
前馈神经网络可以在不同维度上进行学习,增加模型的非线性特征,同时引入残差连接和归一化层,避免因层数叠加导致的梯度消失和过拟合问题,公式如下:
其中,LayerNorm(⋅)表示归一化层;relu(⋅)表示激活函数;w1、w2表示全连接网络的参数矩阵;b1、b2表示全连接层的偏置值。
为了在Transformer 层中有效地融合不同时刻的兴趣偏好特征,本文在Encoder-block的基础上引入了注意力网络对不同时刻的特征进行聚合,探索待推荐项目与兴趣偏好特征之间的关系,从而得到用户的长期兴趣偏好,公式如下:
其中,fatt(⋅)表示注意力网络;表示Encoder-block输出的第j个的兴趣偏好;wl表示注意力网络的参数矩阵;bl为偏置值;αj表示第j个兴趣偏好的权重值,计算公式如式(10)所示,其中δ(⋅)函数表示计算不同特征之间的权重系数:
2.4 全连接输出层
为了有效地捕捉到用户的全局偏好,本文从用户和项目的嵌入矩阵中检索出用户u和目标项目i的嵌入向量,并与多尺度时序卷积层和Transformer 层提取的细粒度长短期兴趣偏好进行融合,通过全连接输出层建模用户-项目的交互关系,得到在t时刻用户u点击目标项目i的概率,公式如式(11)所示:
其中,wo表示输出层的参数矩阵;bo表示输出层偏置值;sigmoid(⋅)表示激活函数。
本文在训练中优化的目标函数为二元交叉熵损失函数,为防止训练中出现过拟合现象,在目标函数中引入L2正则化,对偏差较大的参数进行限制,公式如下:
其中,y表示用户对目标项目的真实标签;表示模型输出的预测标签;λ为正则化因子;w表示模型所有有效参数。
2.5 复杂度分析
对于TAIP 模型的复杂度,本文对多尺度时序卷积层和Transformer层进行了分析。假设嵌入向量在隐藏空间中的维度为d,用户行为序列的长度为n,时序卷积网络的尺度为m,卷积核大小为k。
在多尺度时序卷积网络层中,每个尺度上都需要进行卷积核为k的因果卷积操作,复杂度可以表示为O(mnk);在通道和空间注意力上需要对各尺度输出进行相似度计算,复杂度可以表示为O(mnd)。由于k≤n 在Transformer 层中利用了多头注意力机制计算序列中每个行为之间的相似性,以及利用了注意力网络去融合了不同时刻的特征信息得到用户的长期偏好,两部分的复杂度均为O(n2d),所以Transformer 层的时间复杂度可以表示为O(n2d)。 综上所述,本文提出的TAIP 模型复杂度可以归纳为O(n2d+mnd),从复杂度可以看出,模型的复杂度主要与用户序列长度、嵌入向量维度和尺度数有关。 为验证TAIP 模型的有效性,本文在两个公开数据集上进行实验。MovieLens-1M(以下简称ML-1M)数据集是一个电影推荐场景的数据集,包含了6 040 名用户对3 706部电影的1 000 209条评分数据,评分值为[1,5]之间的整数,每名用户交互的序列长度超过20;YELP数据集是Yelp公司提供的商户评分数据集,包含42 715名用户对31 765个商户的2 163 945条评分数据,评分值为[1,5]之间的整数,每名用户交互的序列长度超过10。两个数据集的具体统计信息如表1所示。 表1 实验数据集的统计信息Table 1 Statistics of experimental datasets 本文采用Leave-One-Out 评估策略,将用户最近交互的行为信息作为测试集的正样本数据,并随机从用户未交互的项目集中抽取100 个项目作为测试集的负样本数据,其余的交互行为作为训练集数据。 本文使用的评价指标包括HR@N、NDCG@N 和MRR:其中命中率(HR@N)用于衡量长度为N的推荐列表中包含正样本项目的比率,公式如下: 1967年,彼得·卡尔·戈德马克提出了新媒体这一概念,但学术研究发展至今,学界也未能给予新媒体准确定义。有专家认为,以数字及互联网技术为基础,向人们提供信息技术服务就可以称为新媒体;但也有专家表示,在传媒中进行高新技术的有效运用就可以称为新媒体。在笔者看来,新媒体应该是在信息技术支持下,具有海量性、交互性以及共享性特点的一种向受众提供信息服务的媒介形式。 其中,U表示所有用户集合;idxu,i表示用户u测试集合中的正样本项目i在推荐集合中的下标;1(idxu,i 归一化折扣累计增益(NDCG@N)用于衡量推荐列表中正样本项目在不同位置的相关性,排序越靠前,推荐效果越好,公式如式下: 平均倒数排名(MRR),用于衡量正样本在推荐列表中的位置关系,位置越靠前,推荐效果越好,公式如下: 其中,idxu,i小于N取值为idxu,i,大于N取值为+∞。 为有效地评价TAIP 模型的推荐效果,本文选择了以下具有代表性的模型进行比较: (1)NCF[9]:扩展了传统的协同过滤算法,利用用户和项目的嵌入向量在全连接网络中刻画用户与项目之间的交互关系。 (2)BST[17]:使用了单向Transformer 编码器去捕获用户的行为序列中的关系,并融合用户和项目的其他属性提供序列推荐。 (4)BERT4Rec[20]:将NLP 领域的BERT 模型引入到推荐模型中,使用双向的Transformer 编码器捕捉用户行为序列中的关系提供序列推荐。 (5)MPM[16]:训练了一个行为检测器判断兴趣爱好对目标项目的影响,并融合一般特征进行推荐。 (6)SRMA[21]:采用模型增强的方式对模型进行扩充,从而提高模型的推荐性能。 (7)ContrastVAE[22]:将用户的行为数据映射到两个不同的隐藏空间,并利用多个Transformer从两个空间中估计相应的后验概率分布,最后再通过一个Transformer执行推荐任务。 (8)DuoRec[23]:采用对比正则化的方法重塑用户行为序列的表示分布,并利用无监督和有监督的对比样本进行建模学习,从而完成推荐任务。 本文的实验在Linux 操作系统上进行,模型实现采用Pytorch 深度学习框架,并在NVIDIA RTX 2080Ti GPU 上进行训练。实验中对常见的超参数进行如下设置,嵌入向量的维度在[8,16,32,64,128]之间调整,初始学习率为0.001,正则化系数为0.001,优化器为自适应梯度下降(Adam),dropout 比例为0.2,批处理大小为256,序列长度在[5,10,20,50,100]之间调整,评价指标N取值为[1,10]。对比模型的其他超参数遵循其作者原有的设置。 3.4.1 模型性能分析 在ML-1M 与YELP 两个数据集上对所有模型进行了测试,各模型的性能结果如表2和表3所示,其中最优的结果采用加粗表示,并在最后一行展示了TAIP 模型相较于次优结果的提升比率。 表2 ML-1M数据集上的推荐性能比较Table 2 Performance comparison on ML-1M dataset 表3 YELP数据集上的推荐性能比较Table 3 Performance comparison on YELP dataset 从表2 和表3 中可以得出结论,采用神经协同过滤的NCF 模型与其他模型相比,在各项评价指标上均低于其他模型,这是由于NCF 模型仅考虑了用户的点击信息,而忽略了用户行为序列之间的特征信息。 在基于用户行为序列的模型中,Caser 模型的性能低于MPM 模型,表明时序卷积相较于传统的卷积网络具有更好的学习能力,这是因为时序卷积的结构可以获得更大的感受野;BST 模型的性能低于BERT4Rec 模型,表明利用双向Transformer 编码器对用户的行为序列进行建模比单向Transformer编码器具有更好的学习能力;对于SRMA、ContrastVAE和DuoRec模型,其性能仍低于TAIP模型,表明仅考虑模型增强和数据增强,对模型性能的提升有限。 从表2、表3 中结果可知,相较于次优模型,TAIP 模型在两个数据集上,HR@10评价指标分别提升了4.84%和2.57%;在NDCG@10 评价指标上分别提升了6.01%和3.22%;在MRR 评价指标上分别提升了10.38%和3.37%。其中MRR 指标提升最为明显,表明TAIP 模型对正样本的识别能力较强。 综上所述,本文提出的TAIP模型,相较于其他模型具有较大的提升,表明用户交互的时间间隔信息和用户的长短期兴趣偏好对模型性能的提升具有重要作用,验证了TAIP模型的有效性。 3.4.2 嵌入向量维度分析 在隐藏空间中,不同维度的嵌入向量对特征的表示能力是不同的,对推荐性能的影响也是不同的,本文对不同嵌入维度对推荐性能的影响进行了实验,实验结果如图4 所示。本部分仅展示了NDCG@10 和MRR 评价指标的实验结果,其他评价指标具有相同的趋势。 图4 不同嵌入向量维度的对比图Fig.4 Comparison of different embedding dimension 通过图4 对比分析可知,随着嵌入向量维度的增加,模型的性能会越来越好,这是由于在嵌入向量维度较小时,模型的参数较少,限制了模型对用户信息的学习,从而导致性能不好;在嵌入向量维度较大时,模型能更好地学习到用户的隐藏信息,提升模型的推荐性能,但较大的维度会大幅度增加模型计算量,使得收敛所需要的时间更长,同时也会让模型出现过拟合现象。在两个数据集上,TAIP 模型在维度达到128 时,具有最佳性能,因此在两个数据集中嵌入向量维度设置为128。 3.4.3 行为序列长度分析 图5 展示了两个数据集上用户行为序列长度对推荐模型性能的影响,序列长度的取值范围从5到100,本部分仅展示了评价指标HR@10和NDCG@10的实验结果,其他评价指标具有相同的趋势。 图5 不同序列长度的对比图Fig.5 Comparison of different sequence length 从图5 分析可知,随着序列长度的增加,模型的性能趋向于平稳。对于数据密度较大的ML-1M 数据集,性能曲线呈现上升后再下降的趋势,在序列长度为20时,达到了最佳性能。在数据密度较小的YELP数据集中,性能曲线同样呈现上升后再下降的趋势,在序列长度超过10 后,性能开始趋向于平稳下降,这是因为在YELP 数据集中较长的序列引入更多的噪声,使得性能退化。因此在ML-1M 数据集上序列长度设置为20,YELP数据集上的序列长度设置为10。 3.4.4 超参数分析 图6展示了两个数据集上不同的Dropout比率和学习率对TAIP 模型的影响。从图6(a)可以看出,在两个数据集上随着Dropout比率的增加,TAIP模型的推荐性能逐渐下降,在Dropout 比率超过0.5 时,推荐性能的下降幅度较大,这是由于较大的Dropout 比率减少了有效参数,导致模型无法学习到足够的特征,从而降低模型的性能。从图6(b)可以看出,较大的学习率会导致模型的推荐性能处于较低水平,这是因为模型在训练过程中无法收敛到最优解;较小的学习率会导致模型在训练过程中收敛缓慢,需要更多的迭代才能达到最优解,同时也会让模型陷入局部最优解,无法达到更好的性能。因此在ML-1M数据集上,Dropout比率设置为0.2,学习率设置为5E-4;YELP数据集上,Dropout比率设置为0.2,学习率设置为5E-4。 图6 不同超参数的对比图Fig.6 Comparison of different hyperparameters 3.4.5 优化器分析 为分析不同优化器对性能的影响,本文在两个数据集上选取SGD、Adagrad、RMSprop 和Adam 优化器进行了对比实验,实验结果如图7所示。 图7 不同优化器的对比图Fig.7 Comparison of different optimisers 从图7中可以看出,在两个数据集上不同的优化器具有不同的收敛速度,其中SGD优化器的效果较差,其主要原因是在随机梯度下降的时只考虑了一个样本,导致在参数更新时出现较大的偏差,从而陷入局部最优解,无法得到较好的推荐性能;Adagrad优化器可以在训练过程中自动调整模型中每个参数的学习率,从而获得更好的训练效果,相比于SGD优化器提升明显;RMSprop是在Adagrad上改进的梯度下降算法,该算法中结合了历史梯度信息去动态的调节学习率,使得模型具有良好的训练效率;Adam优化器结合了RMSprop和动量梯度下降算法,使得模型在训练过程中能获得较好的收敛速度,相较于其他优化算法具有一定的优势。 3.4.6 消融实验分析 在TAIP模型中,分别引入了时间位置信息、多尺度时序卷积层和Transformer 层,为了验证各组件的有效性和对模型性能的影响,在两个数据集上的设计了消融实验进行研究分析,实验结果如表4所示,实现细节如下: 表4 消融实验结果Table 4 Results of ablation analysis (1)Short:忽略TAIP 模型中的Transformer 层,只保留多尺度时序卷积层提取的短期兴趣偏好作为全连接层的输入。 (2)Long:忽略TAIP 模型中的多尺度时序卷积层,只保留Transformer层获取的长期兴趣偏好作为全连接层的输入。 (3)Relative:去除TAIP 模型中的时间位置信息,采用序列的相对位置信息,探索时间位置信息对TAIP 模型性能的影响。 从表4的实验结果可以得出如下结论: (1)Short 模型与TAIP 模型相比,在各评价指标上的性能相差较大,表明在模型中仅使用用户的短期偏好对模型性能的提升有限。 (2)Long 模型与TAIP 模型相比,Long 模型的推荐性能有所退化,表明在模型中仅使用用户的长期偏好对模型性能的提升也有限。 (3)Short 模型与Long 模型相比,Short 的性能要低于Long 模型,表明通过Transformer 编码器探索用户的长期兴趣偏好对模型性能的提升更为重要。 (4)Relative 模型与TAIP 模型相比,采用绝对位置信息的Relative 模型推荐性能有所下降,表明用户的时间位置信息加入到用户行为嵌入矩阵中可以有效地提升模型的推荐性能。 综上所述,表明TAIP 模型的各组成部分对性能的提升具有积极作用,验证了各组成部分的有效性。 3.4.7 注意力机制分析 在TAIP 模型的多尺度时序卷积层中,利用了通道和空间注意力计算不同尺度特征之间的重要程度,为了验证有无注意力和不同类型的注意力对推荐性能的影响,在两个数据集上的设计了实验进行研究分析,实验结果如表5 所示,其中None 结构表示不使用注意力机制,采用直接加和的方式融合不同尺度的输出;Self-Attention 表示使用自注意力机制替代通道和空间注意力机制;Multi-Head表示利用多头注意力机制替代通道和空间注意力机制。 表5 多尺度时序卷积层注意力机制实验结果Table 5 Results on attention mechanism for multi-scale TCN 从表5的实验结果可以看出:采用直接加和的方式融合各尺度的特征会让推荐模型的性能退化,表明使用注意力去融合各尺度的特征是有效的。采用通道和空间注意力机制去融合各尺度的特征,相较于自注意力机制和多头注意力机制具有一定的优势,这是因为通道和空间注意力更能识别出卷积网络输出的通道和空间维度特征,从而提升性能。 在TAIP 模型中,Transformer 层也使用了注意力机制,为了验证有无注意力和不同类型的注意力对推荐性能的影响,在两个数据集上的设计了实验进行研究分析,实验结果如表6所示。 表6 Transformer层注意力机制实验结果Table 6 Results on attention mechanism for Transformer 从表6的实验结果可以看出,在ML-1M数据集上,不使用注意力机制推荐模型的性能退化严重,表明在Transformer层中注意力机制对性能的提升尤其重要。在YELP 数据集上三个结构的性能相差不大,这是由于在数据密度较小YELP数据集中,每名用户的有效序列长度较短,使得注意力机制无法从序列中学习到足够的有效信息去提升推荐性能。 3.4.8 复杂度分析 对于模型的复杂度,本文与MPM、SRMA、ContrastVAE和DuoRec模型在复杂度和训练时间效率[24]上进行了对比分析,对比分析结果如表7 所示。设嵌入向量在隐藏空间中的维度为d,用户行为序列的长度为n,时序卷积网络的尺度为m,卷积核大小为k,经分析各模型的复杂度从小到大的排列如下:MPM 表7 不同模型复杂度比较Table 7 Complexity comparison about different models 本文提出了一种融合时间感知与兴趣偏好的推荐模型,将用户交互的时间间隔信息作为辅助信息引入到序列嵌入矩阵中,并设计多尺度时序卷积网络与通道和空间注意力机制精准地提取细粒度短期偏好;同时采用Transformer 编码器挖掘目标项目与用户兴趣之间的长期偏好;最后利用了全连接网络实现全局特征融合,再提供推荐。在两个公开数据集上的实验结果表明,所提出的TAIP模型优于其他模型,验证了模型的有效性;消融实验也证实了各组成部分对推荐性能的提升具有积极作用。 在未来的工作中,将考虑使用图神经网络对用户的社交信息进行学习,获取用户的社交特征,从而进一步提高模型的推荐性能,以及引入更多的辅助信息,建立一个更加健壮的推荐模型。3 实验与分析
3.1 实验数据集

3.2 实验评价指标
3.3 对比模型与参数设置
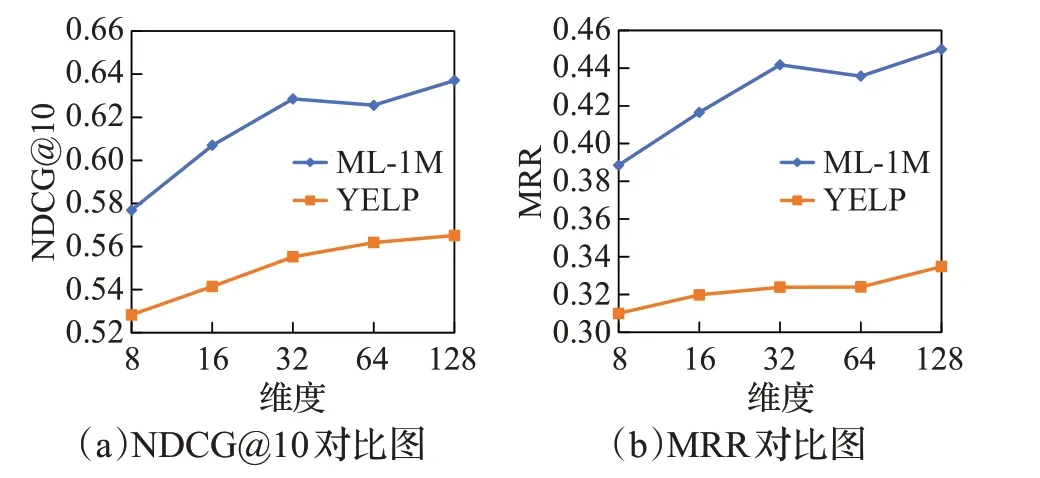
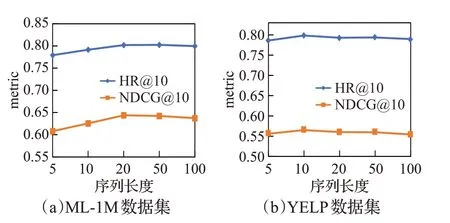
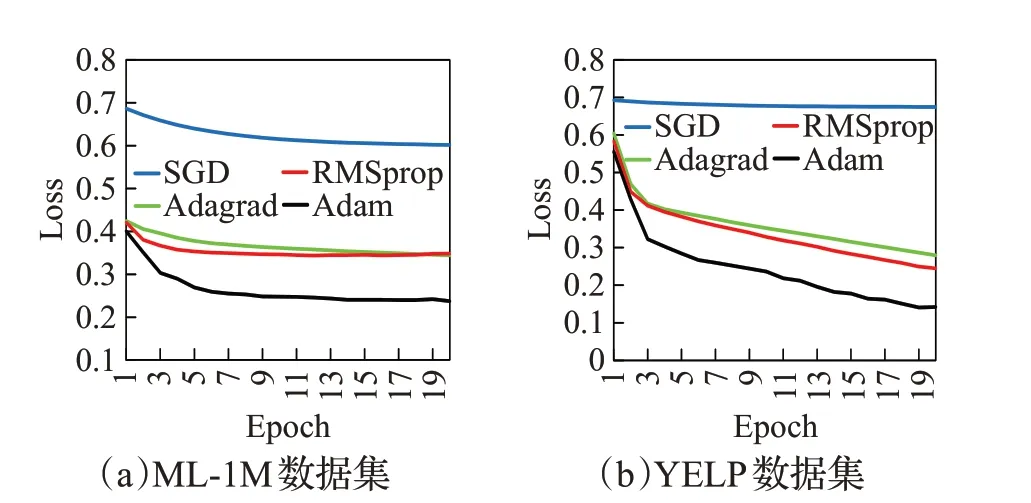
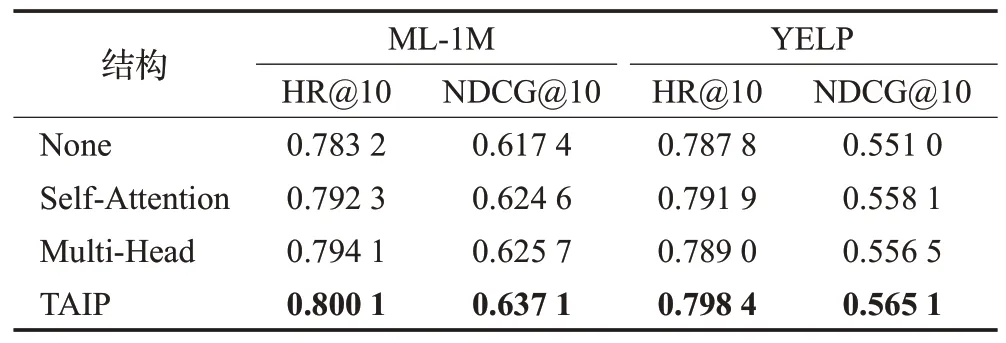
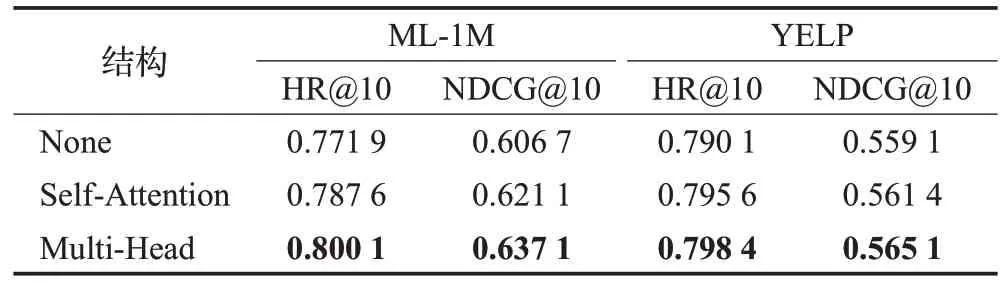
3.4 实验结果及分析




4 结束语

