k 近邻密度支配域代表团密度峰值聚类算法
吕鸿章,杨易扬,,杨戈平,巩志国
1.广东工业大学 计算机学院,广州 510006
2.澳门大学 计算机与信息科学系,澳门 999078
聚类分析是处理数据分析发掘知识的重要手段。其中,密度聚类在应对非凸数据集时,具有很强的健壮性[1]。利用核密度估计,可以灵活地发掘数据中任意形状的簇。从而被广泛用于计算机视觉、目标检测等场景[2]。MeanShift是经典的密度聚类算法,它利用密度爬山的策略重塑样本分布,每个样本点朝密度增加最大的方向,即核密度加权均值处移动,直到所有点收敛于局部密度峰值处,最终得到聚类结果[3]。具有较强的理论基础和健壮性,但因为考虑了eps带宽参数,导致其会出现过少分割和过度分割的情况。此外,该算法不能产生指定簇数目K的聚类结果,即不满足K划分需求。MeanShift 在样本量十分庞大时,由于每次移动都需要计算核密度加权均值向量,因此会非常耗时[4]。为了避免上述核密度加权均值点的重复计算,Sheikh 等人[5]于2007 年ICCV 上提出Medoidshifts,它将每个数据点的移动方向设定为实际存在的样本点,而且沿着该方向密度增加最大,所有这些点组成的有向路径的终点为实际存在的局部密度峰值点。最后形成若干棵树,每棵树聚成一类。该算法在估计密度和判别方向时候还是考虑了所有样本点,不适合大规模聚类,而且依旧带有eps参数的缺陷。Vedaldi 等人[6]在2008 年ECCV 上的QuickShift 算法改进了Medoidshifts 减少了计算样本点移动方向的负担,它直接考虑tau半径内的样本点,以tau半径邻域内最近且密度更大的点为下一个移动方向。该思想也是密度支配思想的运用,然而带宽参数影响依旧没有消除。Jiang 等人[7]在ICML 2018 上的QuickShift++使用mutualk-NN图生成种子簇来替代上述移动路径的峰值终点,一定程度上解决了过度分割的问题,也具有QuickShift 计算量较少的优点。然而上述所有针对MeanShift的改进均未能实现K划分。
除了mutualk-NN图以外,密度支配距离也可以作为解决过度分割的另一途径,而且实现方式更简单。密度峰值聚类DPC算法便是结合了密度及密度支配距离的聚类算法,它于2014年发表在Science上。该算法简洁明了,直接综合考虑样本点的密度和密度支配距离快速获得簇心,再利用支配关系构建的支配树,从簇心峰值处由上到下实现聚类[8]。此处密度支配关系类似上文QuickShift算法,只不过DPC 的考虑范围涵盖所有样本点。密度支配距离使得簇心选择不易集中,同样缓解了密度聚类中过度分割的情况。将密度支配距离与各样本点密度值相结合,例如直接相乘算子γ值,还可以选择指定数目的簇心,从而实现密度聚类中指定簇数目K的K划分聚类。
虽然DPC算法思想简明且具备许多密度聚类不具有的优点。但面对大规模的样本数据,效率依旧不高,主要体现在为每个点建立支配关系的过程上[9]。为此,增强DPC 应对大规模聚类能力具有很大意义,许多研究人员对此问题提出了不少方案。有的工作集中在使用大数据框架进行改进[10],有的则使用空间划分索引树的方式来简化核密度估计和参数调整[11],有的则使用小团簇划分和代表点的方式减少聚类任务负载,从而实现加速的效果[12-13]。其中以小团簇代表点来增强的方式是近几年解决此类问题的常用思路。
2019 年Zheng 等人提出的QuickDSC(clustering by quick density subgraph estimation)则使用mutualk-NN的方式构建小团簇,以小团簇密度峰值点作为代表点,最后参照DPC的思路利用关键小团簇代表点间的支配关系合并小团簇,从而完成聚类[12]。不仅有效地改进了QuickShift++不能实现指定数目K的聚类的缺陷,还极大地提高了DPC 的速度。与QuickDSC 类似,2022 年ECML PKDD 上的FastDEC(clustering by fast dominance estimation)算法首次提出k-NN 密度支配域小团簇生成方式,并将此运用至DPC 的改进中。相比较依靠mutualk-NN连通性生成小团簇,它直接使用k-NN范围内的密度支配规则生成密度支配域作为小团簇,将团簇内密度峰值点作为代表点。因此,FastDEC只关注各支配域代表点,以点代面执行DPC 完成聚类。这使得DPC的效率得到进一步提高。此外,k-NN密度支配域的并集涵盖所有样本点,省去了考虑偏僻样本点的时间,产生团簇的方式也更直接[13]。
k-NN 密度支配域的改进策略其效果虽然显著,但存在代表点代表能力不足的问题。在密度支配域规模较小时,单个峰值代表点有能力代表整个支配域进行聚类,但密度支配域过大时,支配域的形状也会任意变动,此时仅仅一个代表点不足以代表整个支配域,导致聚类出现错误。因此,增加代表点,从密度支配域中采样少量代表团可以作为解决这个问题的一个思路。然而,仅仅是随机采样依旧不能保证选出来的代表可以具有代表性。因此,可以参考KMeans++的初始化思路来优化代表团的产生过程[14]。这样产生的代表团能够更好地反映一个团簇的分布状况。由于各支配域的代表从单个代表点变成了代表团,密度支配域间的距离衡量也是一个挑战。对此,采用高斯核加权平均的方式计算两两支配域间的距离也是可供考虑的解决方案。解决了支配域距离衡量的问题,DPC 算法便可以继续执行,尽管相比较FastDEC减少了一些效率,但依旧可以应付大规模聚类问题,更关键是聚类质量得到了保证,这便是新的密度聚类算法DWG-DPC(delegations weighted-Gaussian similarities based density peaks clustering)。
综上,密度聚类具有很好的健壮性,DPC 算法是密度算法中支持K划分需求的算法,但不适合大规模数据集聚类。k-NN 密度支配域小团簇加速是解决该问题的一个思路,但面临代表代表能力点不足的缺陷。新算法DWG-DPC采用密度支配域团簇生成方式,以代表团策略改进了k-NN 密度支配域代表点代表能力不足的缺陷,它继承了密度支配域的高效优点和DPC 的聚类特性。为了使代表团的代表能力更强,借助KMeans++的初始化方式进行采样优化。针对域间距离的度量问题,提出了一种以近邻关系为主的高斯核域间加权距离计算方式。DWG-DPC 在继承密度支配域小团簇策略快速聚类优点的同时,也保证了聚类质量,更满足指定数目为K的聚类需求。对聚类分析工作具有一定的实用性。
1 预备知识
本章主要介绍密度支配,小团簇代表点聚类加速技巧和密度支配域。为方便介绍上述概念,先规定如下符号。算法的输入数据集为X∈ℝn×m特征矩阵。样本个数为n,任意样本xi∈X,xi∈ℝm。小写k代表近邻数,大写K代表聚类簇数。Ti表示密度支配域或密度支配树。TS={Ti}表示密度支配域集合或密度支配森林。sub表示各对象的密度支配从属关系,sub(xi)=xj表示xi的上级密度支配点为xj。N(xi)表示xi的近邻节点集,根据衡量方式的不同有k近邻Nk(xi)和r半径近邻Nr(xi)。dist(xi,xj)表示xi与xj的距离,通常是欧氏距离‖xi-xj‖。δi表示xi的密度支配距离。kde(xi)为核密度估计函数用于估计点xi的密度ρi,核密度估计可选择平核、高斯核等[15],如公式(1)、(2)所示:
密度支配的概念源于DPC 算法,它将离样本点xi最近且密度比xi更大的点作为上级密度支配点。该算法的思想是通过综合考虑每个点的密度ρi和密度支配距离δi快速得到簇中心,最后利用全域密度支配关系由上到下传播类标签完成聚类。FastDEC 继承了该思想,它将支配关系由全域X拓展到k近邻Nk(xi)下。此时,全域的密度支配范围X则是k=n时的特殊情况。如不考虑具体的近邻衡量方式,则密度支配规则可描述为[8,13]:
定义1(密度支配)对∀xi∈X,如果∃xj∈X,xj=,则称xi被xj密度支配或xj密度支配xi,点xj称为xi的上级密度支配点,记作sub(xi)=xj。否则,xi为全局密度峰值点,sub(xi)=xi。
在DPC中,对于全局密度峰值点,它的密度支配距离设置为已有δ值的最大值,以保证该点能入选为簇心。除此之外,δi=dist(xi,sub(xi))。由于每个点要么没有密度支配上级,即全局密度峰值点,要么只有一个密度支配上级,由此而形成了树状密度支配关系。
利用代表点的处理结果粗略得到整体的运行结果是应对大规模聚类的实用技巧,如mini batch Kmeans中的小批次样本点[16]。LSC(landmark-based spectral clustering)算法中的Landmark代表点[17]。小团簇合并加速聚类属于其中一种,核心思想是将样本集分为p个互不相交的小团簇,p≪n。每个团簇选出一个代表点,通过聚类少部分代表点来实现所有样本点的聚类。从而提升一些聚类算法应对大规模聚类的能力。不同于原始的代表点思路,小团簇合并加速技术需要先构建小团簇,然后再从中得到代表点。
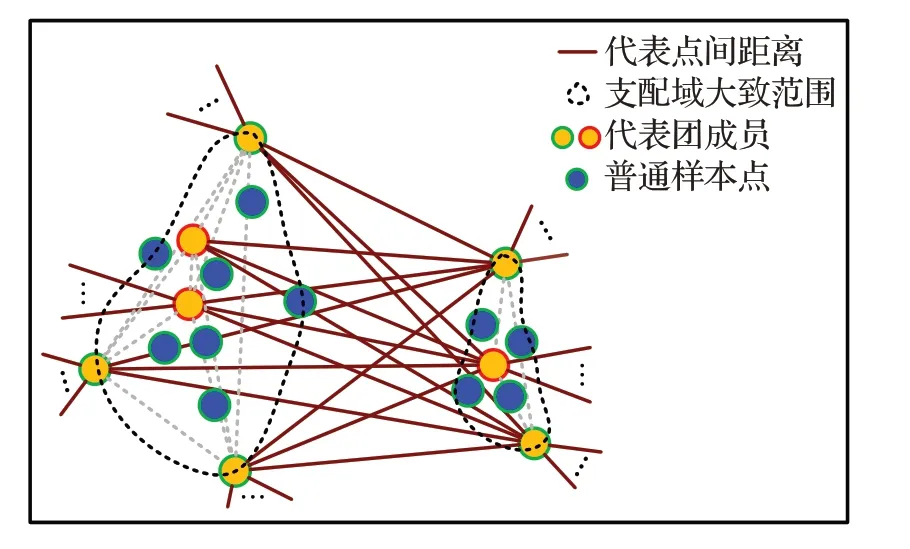
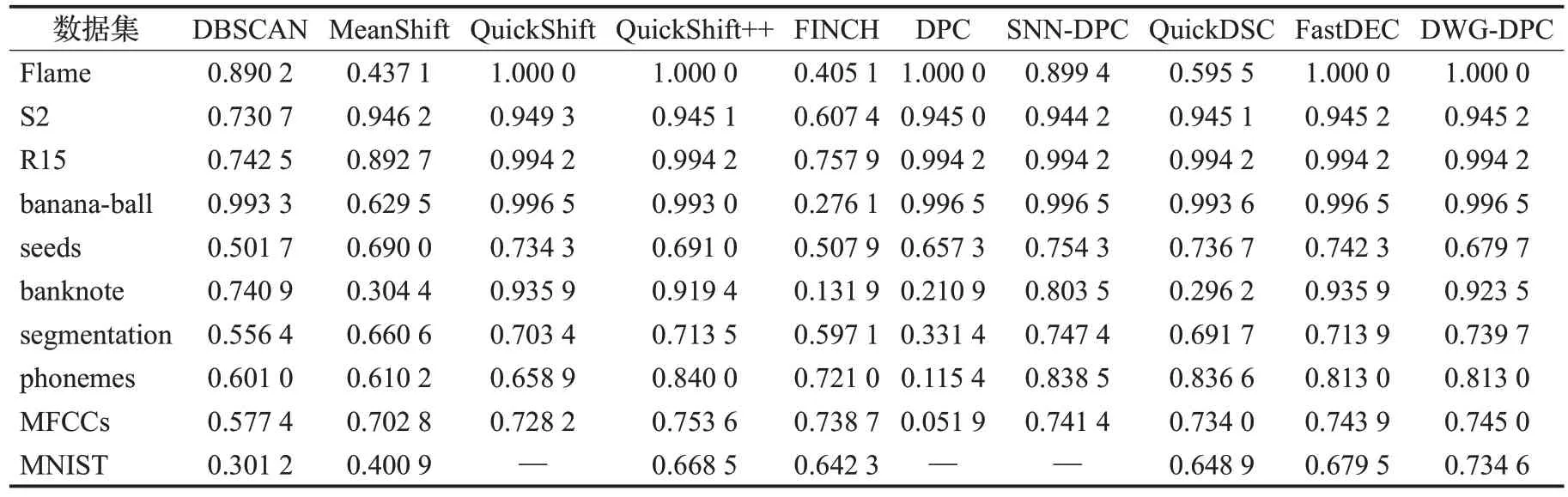
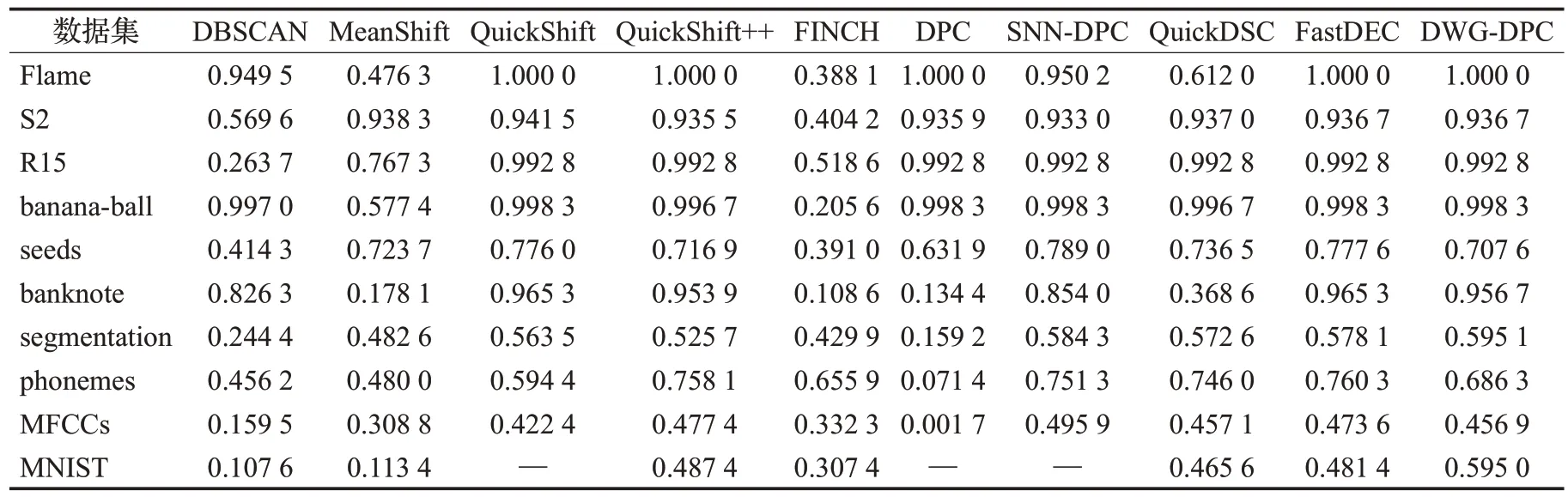
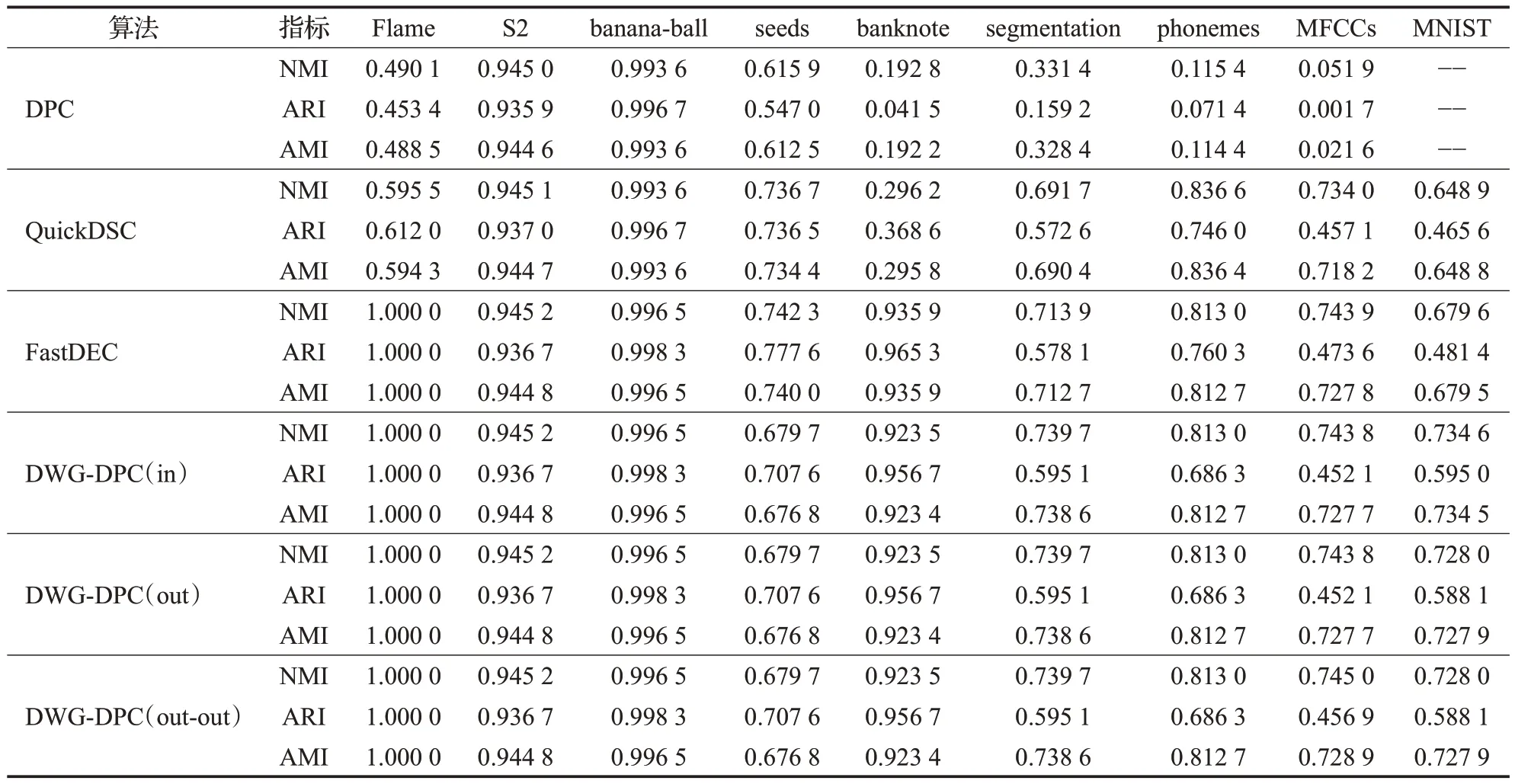
已有的小团簇生成方式有如Quickshift++中的mutualk-NN mode 生成方式,FastDEC 中k-NN 密度支配域生成方式。前者需要在建立k-NN 的基础上遍历探寻mutualk-NN,之后还得归类未在mutualk-NN中的边缘样本点。后者在k-NN 图的基础上直接使用密度支配规则形成支配域。由于k-NN的限制,原始的DPC密度支配关系树就划分成若干棵小树,成为密度支配森林。其中,每棵小树即为一个支配域。令sub(x)w表示x的w阶上级密度支配点,即在密度支配关系树上对x连续求w次父节点,0 定义2(密度支配域)对于非空集合Tj⊆X而言,如果∃w和yj∈Tj使得sub(xi)w=yj对∀xi∈Tj都成立,则Tj是以yj为峰值点的密度支配域。 k-NN 密度支配域代表点技巧在极大提升DPC 速度的同时也存在峰值代表点代表能力不足的问题。在团簇规模小的时候,单个密度峰值点的代表性尚可,但在小团簇规模大时,团簇数据分布的凹凸性和不规则性会削弱峰值点的代表能力,从而引起错误聚类。新提出的支配域代表团策略则是对上述问题的改进。如图1所示,从左到右代表两者不同的划分方式。图1(a)表示A,B 和C 三个小团簇初始分布。图1(b)是仅考虑局部密度峰值的情况,图1(c)是理想的合并结果。由于A和C的局部密度峰值代表点更近,因此只考虑峰值代表点就有可能会出现图1(b)的情况,错误地合并A和C而不是A和B。 图1 局部密度峰值点代表能力不足的情况Fig.1 Insufficient representative capacity of local density peaks 针对上文局部密度峰值点代表能力不足的情况,选取更多的代表点组成区域代表团是解决问题的途径之一。但代表团成员的选择方式同样决定着其代表能力的大小。构成代表团后,各区域间的距离衡量也是需要解决的问题。为方便描述,先给出如下符号定义。设代表团规模为rep,高密度候选点占代表团规模比例为α,低密度边缘候选点估计数为Out,密度支配域(小团簇)Ti规模为|Ti|。 从密度支配域(小团簇)中采样代表团,首先需要先确定采样区。高密度点处在本区域内样本分布密集的地方,这些高密度点对周边样本点具有一定的代表能力,所以代表团采样需要考虑高密度成员。其次,对图1(b)中的错误合并方式而言,如果代表点能够反映支配域的空间分布轮廓并将其考虑进合并规则,那么上述错误发生的几率会减少很多。因此,可以考虑在支配域的周边采样部分代表点。而支配域周边的密度通常比较低,所以可以从低密度区进行采样。这样,采样区可以确定为高密度候选区和低密度候选区。 之后就是确定上述采样区的分界,对于一个有序密度序列,如密度降序序列,仅需确定一个低密度区点数Out即可进行高低密度区域划分。对于密度降序序列,密度最小的后Out个样本作为低密度候选区。而对于密度升序序列,则是前Out个样本作为低密度候选区。虽然支配域分布形状是任意的无法给出统一的衡量标准,但是在操作上可以假定一个较为理想的分布情况进行估计。这里给出类似均匀分布的其中d维超正方体分布估计方案。该方案假设所有团簇Ti以d维超立方体的形式排列,中心部分密度一样,边缘部分密度较低。选择它的一个原因是计算上比较方便。这样最外层的低密度边缘点估计数Out可由公式(3)给出: 证明公式(3)证明如下: ∵对长度为(l-2)的d维超正方体Ql-2而言,它的样本点数为|Ql-2|=(l-2)d。 又∵在Ql-2的最外层再增加一层点,数目为Out,使其变成长度为l的d维超正方体Ql,则样本点数为|Ql|=ld。 ∴Out=|Ql|-|Ql-2|。利用l将|Ql-2|用|Ql|表示即可得到,证毕。 注意公式(3)的前提条件,如果|Ti|≤2d则表明支配域太小,无需进行采样,全员参与代表团。只有|Ti|>2d后Out才有值。在DWG-DPC中,Out存在时则需要判断所需低密度代表团规模rep-int(rep⋅α)与Out的关系。rep-int(rep⋅α) 至于高密度代表团,则直接中选择选密度最大的int(rep⋅α)个点。这两次选择可能存在非空交集,因此需要做并集操作。从而形成支配域代表团,上述过程如图2所示。 图2 在支配域A中采样代表团Fig.2 Sampling delegation in dominator component A 为了保证低密度代表点能够尽可能均匀分布在小团簇边缘处,描述其分布状况。算法采用KMeans++的采样思路,即每次从低密度采样区中不放回地选择距离已有样本点集均值最远的一个,使得选择的样本点尽可能分散。需要再次说明,采样能够进行的前提是,低密度采样区足够大,即rep-int(rep⋅α) 算法1SampleDelegates 输入:支配域Ti,代表团规模rep,低密度比例α,样本点密度ρ。 输出:代表团Mi。 步骤1根据公式(3)计算边缘低密度估计数Out。令high=int(rep⋅α),low=rep-high。 步骤2对Ti的每个点,从ρ中获取各点密度并将样本按密度降序排列,用dt表示。 步骤3判断|Ti|与2d的大小关系。如果|Ti|≤2d则进入步骤9;否则,判断low与Out之间的大小。如果low 步骤4取dt最后面Out个点作为低密度候选区,剩余的纳入高密度候选区,初始化集合S1和S2,将低密度候选区点全部加入S1中,选择S1中密度最低的点作为v点。 步骤5将v从S1中弹出加入S2中;计算S2的均值点u;再从S1中选择距离u最远的点作为新的v。 步骤6重复步骤5直到|S2|=low。跳至步骤8。 步骤7直接将低密度候选区全部纳入S2。 步骤8从高密度候选区中取密度最大的前high个作为S3。令Mi=S2∪S3。返回Mi,结束算法。 步骤9直接令Mi=Ti,返回Mi,结束算法。 衡量两个团簇间的距离常用的办法有Jaccard共享近邻,核函数相似度加权或者代表点马氏距离等[18-19]。前文已说单个代表点虽然可以极大地加快团簇距离的衡量,但存在代表能力不足而错误聚类的风险。因此可以借助少量代表团减少上述误差。虽说马氏距离同样可以依靠簇方差进行一定程度的增强,但不能很好地反映团簇形状的分布。Jaccard 共享近邻虽体现了近邻的本质,但权重统一,未能区分成员点的远近。但如果将近邻的思想跟核函数的相似度衡量特性相结合,则可以同时体现近邻关系,也可以体现成员的先后关系,同时给予不同权重。因此,借助域间成员近邻关系和加权平均和核函数这两个想法,可以导出高斯域间相似度的衡量方式。此处给出方案是近邻图链入链出关联概率作为权重进行高斯核进行加权平均。这种方式特地增强支配域间的较近代表点的距离权重,还可以使得各簇进一步区分。 令p=|TS|为支配域个数,代表点集为n′=|MS|,n′≪n。对任意两个支配域Ti与Tj,对MS中每个点建立n′近邻图,并将链入链出数用邻接矩阵An′×n′表示。通过n′近邻图在域间的相互关系。其中,任意两个密度支配域的近邻关系如图3所示。 图3 域间近邻关系Fig.3 Nearest neighbor relationship between dominator component 设域间关联概率为p(Ti,Tj),将其作为高斯核加权权重,则高斯域间相似度WG(Ti,Tj)可表示成公式(4)。因此,该相似度也可称为Weighted-Gaussian 相似度,简称WG相似度[15]。 由于任意两个支配域近邻关系链入链出优先顺序不同,所以此处有三个计算模式,分别是侧重考虑自身链入情况的“in”模式,侧重考虑自身链出其他支配域情况的“out”模式,两者皆考虑的“out-out”模式。结合邻接矩阵An′×n′,这三种模式对应的WG相似度可由公式(5)表示: 有了相似度,支配域间的距离可通过取倒数的形式进行衡量。设上述记录于距离矩阵Dn′×n′中,Ti与Tj之间的距离Dij可由公式(6)得出: 后续只需要把每个支配域当成新的大样本点,将上述距离当成大样本点的距离即可执行传统DPC 算法。取核密度估计函数为kdeG。此时对每个支配域,支配域密度与域间支配距离则分别如公式(7)、(8)所示[8]: 由于n′≪n,算法耗时会明显减少,有力地增强了它在大规模数据集上的聚类能力。 将前文k-NN 密度支配域,支配域代表团策略,高斯域间相似度等关键步骤汇总可得新的密度峰值聚类改进算法DWG-DPC。该算法关键参数只有近邻数k,k越小,近邻探寻范围越小,近邻支配域划分越精细,时间消耗也越大。k越大,近邻探寻范围越大,近邻支配域划分越粗糙,时间消耗也越少。非关键参数有rep、α和mode。默认情况下rep=30,α=0.2,mode=“out-out”。算法DWG-DPC流程如下: 算法2DWG-DPC 输入:特征矩阵数据集Xn×m,簇数目K,近邻数k。 输出:簇标签数组l。 步骤1建立k-NN图G。根据公式(2)进行核密度估计,得到所有点的密度ρ。 步骤2利用G和ρ,根据密度支配规则,构建密度支配域小团簇集TS={Ti}。 步骤3对每个密度支配域Ti根据算法1采样对应代表团Mi,组成代表点集MS=∪Mi。 步骤4利用MS代表点的近邻关系构建各代表点邻接矩阵A。 步骤5利用公式(5)计算WG 相似度。再利用公式(6)计算距离矩阵D。 步骤6利用公式(7)、(8)和密度支配关系计算支配域密度数组与域间支配距离数组。 步骤7令取最大的前K个支配域作为聚类簇心支配域。 步骤8初始化簇心支配域成员的簇标签,利用域间支配关系,传播簇标签,完成聚类。返回簇标签数组。结束算法。 上述算法的Python代码实现已开源于gitee(https://gitee.com/lvhzgit/dwg-dpc)和github(https://github.com/lvhzgit/DWG-DPC)平台上。算法的流程图如图4所示。 图4 DWG-DPC算法流程图Fig.4 Flow chart of DWG-DPC 步骤1 中k-NN 图可用kdtree 空间索引算法构建,时间复杂度约为O(nm2+n⋅lbn),核密度估计复杂度约为O(nkm⋅lbm+nk⋅lbn)[20]。步骤2 构建密度支配域,每个点扫描近邻密度状况,时间复杂度约为O(nk)。步骤3 代表团采样中,快速排序样本密度数组ρ耗时约O(n⋅lbn),之后对p=|TS|个支配域采样代表团,耗时约。步骤4构建邻接矩阵耗时约O(n′2)。步骤5到步骤8的时间复杂度约为O(3p2+p)。由于n′和p远小于n。因此,算法整体复杂度约为O(nm2+n(1+k)⋅lbn+nkm⋅lbm+n)。相比较原始的DPC 算法,核密度估计不需要O(n2m⋅lbm+n2⋅lbn)的复杂度进行全局扫描计算,构建密度支配关系同样不需要O(n2)的复杂度进行全局扫描。当样本数据规模越大时,DWG-DPC的优势就越明显。 本节介绍实验测试,用于描述该算法在聚类中的表现。主要展示本算法与其他9 个密度聚类算法在不同数据集上的表现。除了上文的DBSCAN、MeanShift、QuickShift、QuickShift++、QuickDSC、FastDEC 和DPC,还有FINCH[21]和SNN-DPC[22]。FINCH 是层次密度聚类算法,默认使用一阶近邻进行合并。SNN-DPC 是DPC在合并上的改进,使用共享近邻的方式衡量样本点间的相似性。上述算法参数及其设置如表1所示。 表1 实验算法Table 1 Algorithms in experiments 数据集方面,实验过程中选取了seed、banknote、segmentation、phonemes、MFCCs 和MNIST 共6 个实际数据集。前5 个是UCI 机器学习公开数据集[23],下载链接为https://archive.ics.uci.edu/ml/datasets.php。后一个MNIST 是规模较大的手写数字数据集[24],下载链接为http://yann.lecun.com/exdb/mnist/。另外还有Flame[25]、S2[26]、R15[27]和banana-ball共4个人工数据集。前3个可从http://cs.uef.fi/sipu/datasets/下载,banana-ball 可利用sklearn 工具包,按照Myhre 等人[28]提出的生成方式生成,生成的数据下载链接为https://github.com/lvhzgit/DWG-DPC/blob/main/data/banana-ball.csv。这些数据集的信息如表2所示。 表2 实验数据集Table 2 Datasets in experiments 本部分实验主要用于对比DWG-DPC 和上文所述9 种密度聚类算法的聚类表现,实验中聚类的效果使用调整兰德指数(adjusted rand index,ARI),归一化互信息(normalized mutual information,NMI)和调整互信息(adjusted mutual information,AMI)三个指标进行衡量。这三个指标越接近1,说明聚类的效果越好。分别令真实标签向量,预测标签向量为。由l和可分别导出样本X的K划分Π和。由此可得列联表如表3所示。 表3 聚类列联表Table 3 Cluster contingency table 记max(0,ai+bj-n)=(ai+bj-n)+,根据表3可得ARI、NMI、AMI指标分别如公式(9)~(11)所示[29]: 实验环境为64 位操作系统,Python 3.7 解释器,主要工具包为numpy、sklearn。硬件上,机器的内存64 GB,Intel®Core i7-12700F CPU(2.10 GHz)。对于运行时间超6 h 或报内存错误的情况,其结果将用“—”替代。实验结果如表4~6所示。 表4 实验结果中的NMI指标Table 4 NMI in experimental results 分析表4 的NMI 指标表现可知,表现最好的是QuickShift。该算法在Flame、S2、R15、banana-ball 和banknote 五个数据集上均达到了最高的指标值。但对于规模较大的MFCCs 则表现得相对不强,MNIST 更是无法得出结果。其次便是QuickShift++、SNN-DPC、FastDEC和DWG-DPC。相比较QuickShift而言,Quick-Shift++在phonemes和MFCCs上取得了最高的NMI值。SNN-DPC则在seeds和segmentation上表现最佳。然而对于规模最大的MNIST 而言,只有DWG-DPC 表现突出,NMI分数高达0.734 6。表现最好的QuickShift甚至无法在有限的时间空间内运行出结果。DWG-DPC 在其他数据集中除phonemes和seeds外,都非常接近最佳指标,差距在0.01左右。 对表5 的ARI 指标而言,QuickShift、FastDEC 和DWG-DPC 均在5 个数据集上表现最优。QuickShift 仅在S2有优势,分数为0.941 5。FastDEC则在phonemes上有优势,分数为0.935 9。而DWG-DPC则在segmentation和MNIST 数据集上有优势,尤其是MNIST 表现最优,高达0.595 0。其余数据集距离最佳ARI 差距大多在0.01到0.08之间。 表5 实验结果中的ARI指标Table 5 ARI in experimental results 对表6的AMI指标而言,其结果基本与表4的NMI分数相同。表现最好的依旧是QuickShift。表现其次的是QuickShift++、SNN-DPC、FastDEC 和DWG-DPC,有四个数据集AMI 指标最优。但是对于MNIST 数据集DWG-DPC依旧保持着突出的表现。DWG-DPC在其余非最优的数据集上表现,同样非常接近最优AMI分数,差距大多在0.01左右。 表6 实验结果中的AMI指标Table 6 AMI in experimental results 上述实验结果可知,在数据规模不大时,QuickShift算法表现很好,但不适合应对大规模聚类。DWG-DPC虽然从评价指标上看,表现并非最好,但应对大规模聚类任务效果突出。此外,相比较仅使用单个代表点的FastDEC 来说,DWG-DPC 做到了保持大规模聚类能力的同时改进聚类效果。这就证明代表团改进策略是有效的。当然对于原始的DPC而言,提升更是显著的,首先原始DPC 算法在MNIST 数据集上无法得出结果,但DWG-DPC 不仅可以做到出结果还可以做到最优聚类结果。其次DWG-DPC 还帮助DPC 在某些数据集上提升了聚类质量,如对segmentation的聚类NMI从0.331 4提升到0.739 7,ARI 从0.159 2 提升到0.595 1,AMI 从0.328 4提升到0.738 6。 表4到表6一定程度上证明了DWG-DPC的良好聚类能力以及代表团策略的有效性。但公式(5)的三种WG相似度还需要更详细的测验。第一,需要确定是哪一种模式帮助代表团策略发挥了作用,第二,需要确定这些计算模式它们之间在实验表现中有什么不同。第三,将“out-out”设计为默认选项是否合理。验证实验选择的算法有DPC、QuickDSC、FastDEC,以及三种WG相似度衡量方式下的DWG-DPC。评价指标依旧选择上文中的NMI、ARI和AMI。实验过程中的参数设置和实验环境与实验准备中所述一致。结果如表7所示。 表7 WG相似度有效性测试结果Table 7 WG similarities validity verification results 由表7 的实验结果可知,聚类结果最好的指标分数大都集中在FastDEC 和DWG-DPC 的三个模式中。FastDEC 的三个指标分数在seed 和banknote 上表现得比DWG-DPC 好。但DWG-DPC 的三种模式下的表现在segmentation 与MNIST 上均比FastDEC 更优异。尤其是MNIST 部分的提升是非常明显的,“in”模式下的NMI 由0.679 7 提升到0.734 6,ARI 由0.481 4 提升到0.595 0,AMI由0.679 5提升到0.734 5。“out”和“out-out”模式下的NMI 则提升到0.728 0,ARI 提升到0.588 1,AMI提升到0.727 9。这表明三种WG相似度计算模式,一定程度上帮助代表团策略发挥了作用,但哪一种影响最大则要视具体数据集而定,因此可以作为域间距离的衡量方式。 另外,根据表7 的DWG-DPC 三种计算方式下的指标分数可知,三种模式效果上几乎没什么差别,最大差距也在0.006 左右。另外,针对具体的数据集有时候存在个别最优,虽说默认情况下“out-out”模式不一定最优,但它综合考虑了代表团链入链处关系中的“in”和“out”两种情况。因此,从三种模式的差距来看,将“outout”视为默认情况是合理的。 针对原始密度峰值DPC算法处理大规模数据能力欠缺以及FastDEC 密度支配域代表点代表能力不足的问题,一种新的密度代表团策略和支配域相似度衡量方式被提出。密度代表团策略采用了Kmeans++的采样思想,使得代表团能够更均匀地分布于支配域中,更好地反映支配域的空间分布,从而弥补了单个代表点代表能力不足的缺陷。而针对代表团的域间相似度衡量,新算法采用基于代表团近邻图的概率加权高斯核函数作为相似度衡量方式。使得其更注重代表团中最相近的代表点的距离。使其比一般的均值衡量更加合理。该相似度也可称为Weighted-Gaussian相似度,简称WG相似度。对应的新算法也命名为DWG-DPC。考虑到近邻的连入连处关系有链入链出两种情况,DWG-DPC给出了三种计算方式。“in”模式侧重考虑自身链入情况,“out”模式侧重考虑自身链出其他支配域情况,“out-out”模式综合考虑了前两者。默认的模式为“out-out”。对比实验表明,这种策略不仅可以有效提高原始DPC 算法的聚类质量,增强其应对大规模数据聚类的能力,对Fast-DEC 在大规模聚类任务上的表现也有所提升。进一步的三种模式对比实验表明,这三种可以作为支配域代表团域间相似度的衡量方式,尽管不同数据集各种模式发挥的作用不同,但差距不大,考虑到“out-out”更加一般化,因此将其设为默认模式是合理的。 DWG-DPC算法虽在部分数据集上取得了成就,实验也表明代表团策略配合高斯域间相似度确实有一定效果,但也存在个别效果不好的情况。因此,该算法还有一定改进空间。目前考虑到的改进点如下。第一,各区域代表团的规模是固定的,可以考虑针对不同的支配域大小来灵活设定,进而改进算法。第二,边缘密度点估计可以考虑使用更为一般性的几何空间分布来更好地获取样本数,文中的超立方体均匀分布是一种非常理想的假设,仅仅是为了方便计算。第三,高斯域间相似度只是考虑到高斯核函数的放缩特性,以及近邻图的关联关系得出的比较合理的衡量方式,因此在度量方法上也有提升空间。这些改进点可作为后续DPC算法改进研究的出发点。
2 算法介绍
2.1 密度支配域代表团

2.2 高斯域间相似度
2.3 算法流程

2.4 算法复杂度分析
3 实验介绍
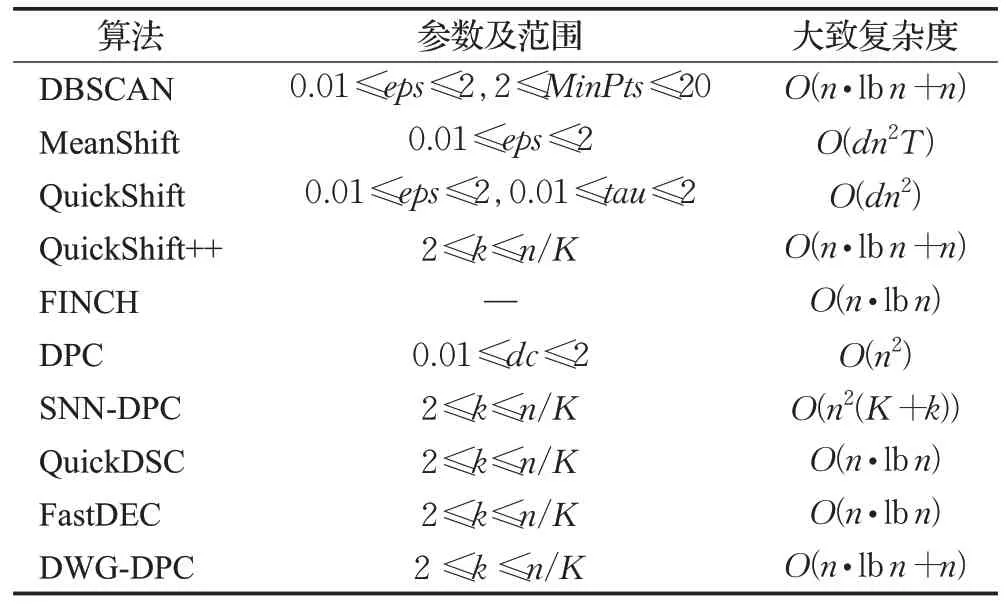
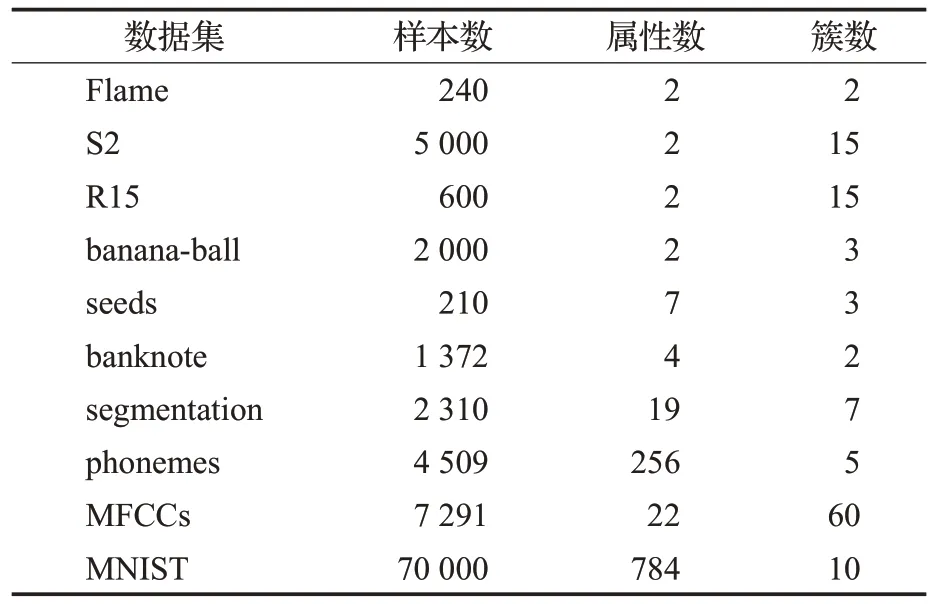
3.1 实验准备
3.2 对比实验


3.3 三种模式下的对比实验
4 结语

