联合三元组嵌入的实体对齐
李凤英,黎家鹏
桂林电子科技大学 广西可信软件重点实验室,广西 桂林 541004
知识图谱(knowledge graph,KG)以三元组(h,r,t)的形式结构化地表示真实世界中的知识,其中h、r、t分别代表头实体、关系、尾实体,知识图谱中的三元组可以直观高效地描述事实。近年来,知识图谱在人工智能领域中发挥了重要作用,如智能问答[1]、搜索引擎[2]、推荐系统[3]等。随着知识图谱所支持的应用的规模不断扩大,单一的知识图谱往往难以满足日益增长的需求,一个有效的解决方案是实体对齐。实体对齐旨在发现不同知识图谱中的等价实体,以等价实体作为桥梁,去融合不同的知识图谱实现知识融合的目的。由于不同的知识图谱往往来自不同数据源,如Freebase[4]与YAGO[5],具有不同的语言形式,因此这些知识图谱具有不同的结构形式(异质性),这给实体对齐任务带来了挑战。
近年来,知识图谱实体对齐的研究方法主要是基于嵌入的方法。基于嵌入的方法将知识图谱嵌入到低维、连续的向量空间中,通过计算向量的相似度发现可能的对齐实体。TransE[6]是最早的知识图谱嵌入方法之一,其将关系视为头实体到尾实体的翻译。一些知识图谱对齐模型采用了基于TransE的方法,如MTransE[7]、JAPE[8]。最近几年,图神经网络在处理图数据上表现优秀,受到广泛关注[9]。图神经网络通过聚合节点的邻域信息学习节点的嵌入表示,许多知识图谱对齐模型采用了基于图神经网络的方法,如GCN-Align[10]、RDGCN[11]、AliNet[12]。最近的实体对齐研究主要采用了图神经网络。图神经网络适合建模图的节点特征,却难以捕获图上的关系信息。根据HGCN[13],知识图谱中的实体与关系通常是密切相关的,丰富的关系信息有助于提高实体对齐的性能。为了学习知识图谱中的关系,RDGCN[11]构造了对偶关系图(将原始图中的节点视为关系,关系视为节点),通过对偶图与原始图的交互捕获了关系信息。HGCN通过实体嵌入计算出关系嵌入,再将关系嵌入拼接回实体嵌入中,实现对关系的学习。RNM[14]通过利用关系的语义信息与映射属性矫正实体对齐。然而,这些方法都忽略了知识图谱中的三元组信息。
知识图谱是由大量的三元组组成,每个三元组由实体与关系组成,图神经网络难以学习到这些三元组信息。考虑三元组信息有利于实体对齐,例如,如图1 所示,其中显示了两个知识图谱,分别来自于DBpedia[15]的中文与英文版本,实体“柏林”与“Berlin”以及“法国”与“French”是等价的,实体“德国”与“German”是需要对齐的实体。三元组(德国,首都,柏林)与(German,capital,Berlin)是等价的,学习这些三元组信息,将有助于提高实体对齐的性能。在知识图谱中,关系是与三元组紧密相关的,考虑三元组不仅可以学习到三元组信息,也会学习到关系信息。此外,关系具有不同的映射属性,如图1 中的“首都”是1-1 的关系,“邻居”是n-n的关系,在实体聚合周围邻居时考虑关系的属性,将有助于得到更加准确的实体嵌入。

图1 实体对齐案例说明Fig.1 Case illustration of entity alignment
为了解决三元组信息利用不充分的问题,本文提出了基于三元组嵌入的实体对齐方法(triple embedding based entity alignment,TEEA)。首先,本文进行初步实体对齐,得到实体嵌入并近似计算出关系嵌入。之后,本文统计出每个实体关联的三元组,计算出三元组嵌入,使用此三元组嵌入作为新的实体嵌入,进行实体对齐的训练。同时,考虑到不同属性的关系,本文在计算三元组嵌入时加入了关系属性约束,并加入了基于TransH[16]的约束,以学习知识图谱中的关系属性。在三个跨语言的数据集上进行实验,结果表明提出的模型TEEA取得了最好的效果。
1 相关工作
近年来,知识图谱表示学习发展迅速,基于表示学习的实体对齐方法越来越多。这些基于表示学习的方法将实体表示为低维向量,然后通过计算实体向量之间的相似度,找到等价的实体对。基于表示学习的实体对齐方法主要分为两类:基于翻译的方法、基于图神经网络的方法。本章将介绍这两类知识图谱实体对齐方法。
1.1 基于翻译的知识图谱实体对齐方法
基于翻译的对齐方法主要是基于TransE[6]及其变体的方法,将关系视为头实体到尾实体的翻译。MTransE[7]首次将TransE 的思想用于实体对齐中。其首先使用TransE学习单个知识图谱的嵌入表示;然后提出三种跨知识图谱的变换方法,将两个知识图谱映射到相同的嵌入空间中;最后对齐不同知识图谱中的实体。IPTransE[17]使用PTransE[18]对每个知识图谱进行嵌入,然后基于种子实体对将两个知识图谱的嵌入变换到统一的语义空间,此外,IPTransE 还提出了迭代扩充种子实体对的策略。BootEA[19]提出了一种自举的方法,该方法在一对一映射的约束下,通过优化一个全局目标将可能对齐的实体加入到训练集中,同时,BootEA 还提出了截断均匀负采样。SEA[20]提出了一种半监督的实体对齐策略,利用有标签的实体和大量无标签的实体信息进行对齐。TransEdge[21]根据关系的上下文(头、尾实体)表示关系,并将关系表示解释为实体嵌入之间的转换。
一些方法使用了知识图谱的额外信息,如属性信息、实体描述信息等。JAPE[8]将两个知识图谱的结构联合嵌入到统一的向量空间中,然后利用知识图谱中的属性改善嵌入表示。KDCoE[22]使用门循环单元(gate recurrent unit,GRU)对实体的描述信息进行编码,并通过基于关系三元组的表示学习进行协同训练,以提高对齐效果。MultiKE[23]通过实体名称、关系、属性三种信息学习实体嵌入,用于实体对齐。
1.2 基于图神经网络的知识图谱实体对齐方法
两个实体的邻域越相似,这两个实体越有可能对齐。图神经网络可以对实体的邻域信息进行建模,因此,越来越多的研究人员利用图神经网络进行实体对齐。
GCN-Align[10]首次将图卷积网络(graph convolutional networks,GCN)[24]用于实体对齐任务,其使用图卷积网络将两个知识图谱的实体嵌入到统一的向量空间。RDGCN[11]构造关系对偶图,通过对偶图与原始图的交互学习关系信息。HGCN[13]考虑了图神经网络中经常忽略的关系信息,首先使用实体信息近似表示关系信息,然后将关系表示合并到实体表示中,以此学习关系信息。MuGNN[25]通过多通道学习知识图谱嵌入,以协调两个知识图谱之间的结构差异。AliNet[12]发现等价的实体往往有不同的邻居结构,因此,AliNet 通过图注意力网络(graph attention networks,GAT)[26]与门控机制引入多跳邻居,以此扩展等价实体之间的邻域结构的重叠。SSP[27]通过利用知识图谱的全局结构与局部语义,以粗到细的方式学习实体表示。NMN[28]采用图采样与跨图邻域匹配的方法评估实体间的相似性,以解决两个知识图谱之间的异质性问题。RNM[14]提出了一种基于关系感知的邻域匹配模型,在匹配邻域时除了比较邻居节点,还考虑了相连关系的语义信息与映射属性。
2 问题描述
知识图谱通常表示为G=(E,R,T),其中E表示实体集合,R表示关系集合,T=E×R×E表示三元组集合。知识图谱是由大量的关系三元组(h,r,t)组成,其中,h,t∈E,r∈R。
给定两个知识图谱G1=(E1,R1,T1)、G2=(E2,R2,T2),预先对齐的实体即训练集表示为S={(e1,e2)|e1∈E1,e2∈E2,e1≡e2},又称种子实体对。实体对齐旨在根据预先对齐的种子,在两个知识图谱间发现新的可能对齐的实体。文中使用加粗的字母表示向量。
3 模型
本文提出了联合三元组嵌入的实体对齐方法。图2展示了TEEA模型的总体结构,其中蓝色虚线表示实体预对齐,蓝色实线表示联合三元组嵌入的实体对齐。模型TEEA 主要分为三个阶段:实体预对齐、计算三元组嵌入、实体对齐。

图2 TEEA模型Fig.2 TEEA model
第一个阶段中,以实体对齐为目标,使用图卷积网络学习到两个知识图谱中实体的嵌入表示,并近似计算出关系嵌入。在第二个阶段,计算出实体相关的三元组嵌入。在第三个阶段,使用上一阶段得到的实体嵌入进行实体对齐的训练;此外,考虑到关系的多种类型,本文加入了关系属性的约束。
3.1 初步实体对齐
3.1.1 实体嵌入
本文使用两层图卷积网络建模知识图谱的结构信息。给定两个知识图谱G1=(E1,R1,T1)、G2=(E2,R2,T2),将其合并为一个知识图谱Ga=(Ea,Ra,Ta),作为图卷积网络的输入,其中Ea=E1⋃E2,Ra=R1⋃R2,Ta=T1⋃T2。对于Ga中的每一个三元组(h,r,t),令A[h][t]=1,其中A是Ga的邻接矩阵。
根据RDGCN[11]的结论,高速门策略可以控制图卷积网络中噪声的传播。TEEA 在图卷积网络的每层中采用高速门的策略:
其中,σ是sigmoid 激活函数,、b(l)分别是门控T(X(l))的权重、偏置,⋅表示逐元素乘法。
得到实体的嵌入表示后,模型TEEA通过衡量两个实体间的距离判断实体是否对齐。对于实体e1∈E1,e2∈E2,两个实体之间的距离计算公式如下:
其中,xe1表示实体e1的嵌入表示,L1 表示L1 范数。距离越小代表实体e1、e2的嵌入越接近,对齐概率越大。
3.1.2 训练目标
本文使用基于边缘的损失函数作为训练目标,使正样本的距离尽可能小,负样本的距离尽可能大,公式如下:
其中,S表示对齐的实体集合,S′表示S的负对齐集合,γe>0 是边缘超参数。
本文使用最邻近采样法得到负样本。对于给定的等价实体对(e1,e2),TEEA 根据公式(4)从实体集合Ea中采样e1(或e2)的前k个最邻近的实体,通过替换e2(或e1)得到e1(或e2)的负样本集合
3.1.3 近似关系嵌入
在三元组(h,r,t)中,关系r是连接头实体与尾实体的桥梁。因此,关系的语义与其相连的头、尾实体相关。给定关系r,其嵌入的近似计算公式如下:
其中,r∈R2×d(l),concat表示拼接操作,hr、tr分别表示与关系r相连的头、尾实体的平均嵌入。最后得到知识图谱中的关系嵌入Y={y1,y2,…,ym|yi∈R2×d},其中,m表示关系数,d表示实体嵌入的维度。
3.2 三元组嵌入
为了利用知识图谱中的三元组信息,本文提出了三元组嵌入的方法,该方法拼接实体周围的关系嵌入与实体嵌入。考虑到知识图谱中关系的类型,不同的关系、尾实体对头实体的影响应该不同。如三元组(中国,首都,北京),“首都”是1-1的关系,关系与尾实体对头实体的影响应较大;三元组(中国,邻接,俄罗斯),因为“邻接”的关系类型,关系与尾实体的影响应较小。本文首先统计出知识图谱中的关系类型。具体地,给定头实体h与关系r,本文定义RelTh_r={ti|(h,r,ti)∈Ta},表示在固定头实体与关系后尾实体的集合。|RelTh_r|=1 时表示关系为1-1 的关系,|RelTh_r|>1 时表示关系为1-n的关系。如图3 所示,为三元组嵌入的计算过程,第一阶段拼接邻居关系,得到联合嵌入,第二阶段拼接邻居尾实体,得到三元组嵌入;在拼接的过程中,考虑了关系类型的影响。
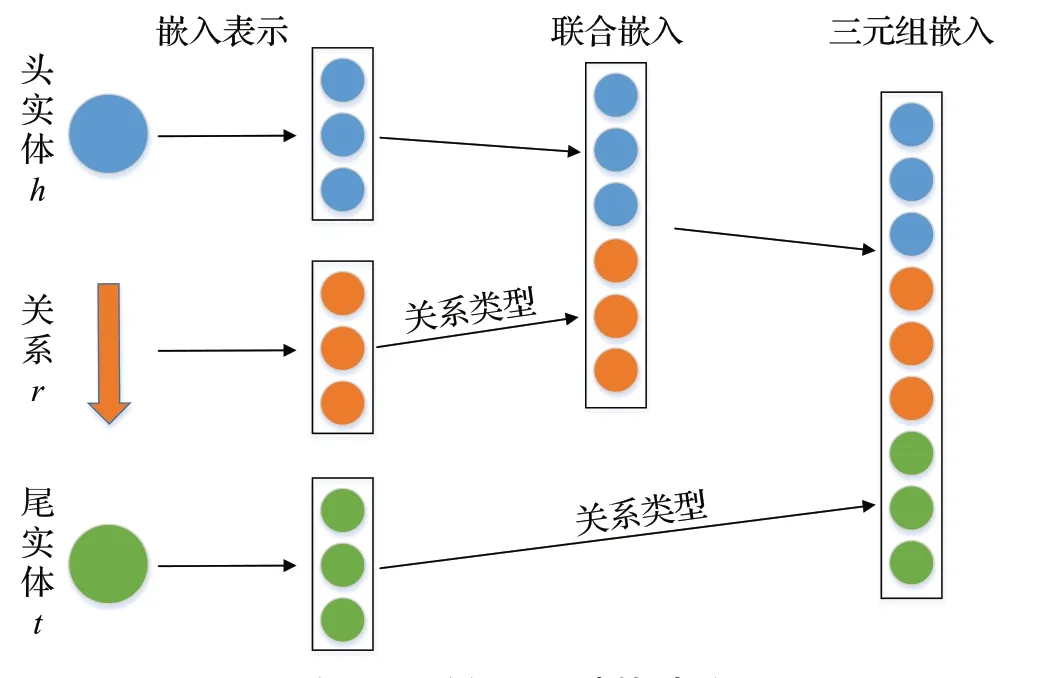
图3 三元组嵌入计算过程Fig.3 Calculation procedure of triple embedding
第一阶段中,考虑关系类型RelT,对邻居关系的拼接分为两步。给定头实体e1∈Ea,其邻居关系集合定义为NRe1={ri|(e1,ri,t)∈Ta},第一步使用如下公式计算邻居关系的加权嵌入之和:
其中,yr是关系r的嵌入表示。第二步,本文将实体嵌入与邻居关系嵌入之和Re1进行拼接,得到联合嵌入ze1:
其中,xe1∈Rd表示实体e1的初步嵌入,WR∈R2d×d是维度变换参数,ze1∈R2d,d表示实体嵌入的维度。
第二阶段中,计算头实体e1的三元组嵌入,其过程分为两步。对于头实体e1,其尾实体集合定义为NTe1={ti|(e1,r,ti)∈Ta},第一步计算邻居尾实体的加权嵌入之和,公式如下:
其中,xt表示实体t的初步嵌入。第二步,本文使用如下公式将联合嵌入与尾实体加权嵌入Te1拼接:
得到三元组嵌入ze1∈R3d。
请注意,TEEA 模型只计算了头实体的三元组嵌入。在得到最新的实体嵌入后,使用ze1进行实体对齐的训练,即将公式(4)中的x换为z。
3.3 关系属性约束
知识图谱中的关系可分为1-1、1-n、n-n三种属性。在实体对齐中,这些关系的属性信息会有助于得到更加准确的对齐结果。TransH[16]是经典的知识图谱嵌入模型,提出了关系超平面的方法,将头、尾实体映射到关系超平面上,解决了TransE 无法学习1-n、n-n的关系的问题。本文将TransH中的关系超平面方法加入到实体对齐任务中,以学习知识图谱中的三种关系属性信息。
本文首先定义关系超平面的法向量矩阵Wr,不同的关系对应不同的法向量。之后,计算头、尾实体映射在关系超平面上的向量。对于三元组(h,r,t),计算方法如下:
其中,h、t表示头、尾实体的向量表示,wr表示关系r的法向量,‖wr‖=1,h⊥、t⊥分别表示头、尾实体在关系超平面上的投影向量。
之后,本文使用如下公式衡量三元组的准确性:
对于正确的三元组,f(h,t)期望值小。
本文使用随机替换头、尾实体的方法获取损坏三元组,之后使用如下损失函数作为训练目标,使正样本的距离尽可能小,负样本的距离尽可能大:
其中,Δ表示正确的三元组集合,Δ′表示由三元组(h,r,t)通过随机替换头、尾实体生成的错误的三元组集合,γt>0 表示边缘超参数。
3.4 总训练目标
本文在实体对齐任务中,加入了关系映射的约束,使用如下的目标函数:
其中,Le_new表示使用三元组嵌入z代入公式(5)中的距离函数得到的损失函数,ε是用于平衡实体对齐损失与关系映射约束损失的超参数。本文使用Adam[29]最小化目标函数Lall。
本文首先使用公式(5)进行实体预对齐,得到实体嵌入,再使用实体嵌入近似计算关系嵌入。之后,本文计算出实体的三元组嵌入,使用此三元组嵌入代入公式(5)中,得到新的损失函数;同时,模型考虑了关系的映射属性,得到联合损失函数Lall。最后使用联合损失函数进行训练。
4 实验
4.1 数据集
本文使用数据集DBP15K[8]评估提出的模型TEEA,该数据集是大规模知识图谱DBPedia[15]的子集。DBP15K包含三个跨语言的数据集:DBP15K_zh-en(中文到英文)、DBP15K_ja-en(日文到英文)、DBP15K_fr-en(法语到英文)。其中每个数据集由两个语言的知识图谱组成,并且提供了15 000 个预先对齐的实体对。此外,每个数据集还包括一些预先对齐的关系。DBP15K 的具体信息如表1所示。根据之前的工作,本文将30%预先对齐的实体对作为训练集,70%作为测试集。
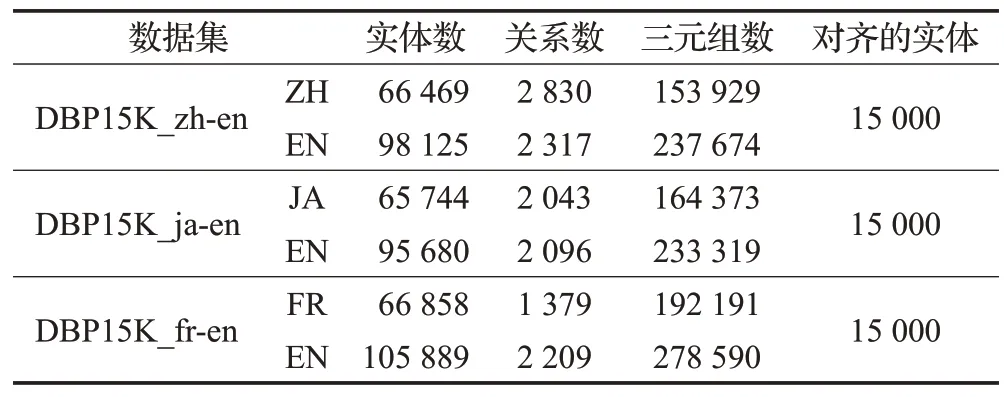
表1 DBP15K数据集信息统计Table 1 Statistics of DBP15K dataset
4.2 基准模型
为了评估提出的模型,本文选择了一些有竞争的实体对齐模型进行比较。主要分为基于翻译的模型与基于图神经网络的模型。
基于翻译的模型有:MTransE[7]、SEA[20]、BootEA[19]、TransEdge[21]。
基于图神经网络的模型有:GCN-Align[10]、RDGCN[11]、HGCN[13]、AliNET[13]、NMN[28]、RNM[14]。
4.3 参数设置与评估指标
本文设置图卷积网络的层数为2,同时其隐藏层维度即实体嵌入维度设为300,设置边缘γe=1,边缘γt=1,ε=0.05。将学习率设为0.001,并且每隔50 个批次为每个正例采样k=125 个负样本。根据RDGCN 中的设置,为了利用实体名称信息,使用谷歌翻译将数据集中的中文、法语、日文的实体翻译为英文,之后使用预先训练好的英语单词向量Glove 构造初始的实体嵌入。训练过程中,第一步使用公式(5)训练50 个批次,第二步使用公式(15)训练10个批次。
与之前的方法相同,本文使用Hits@N与平均倒数排名(mean reciprocal rank,MRR)作为评测指标。共有Ttest个测试实体对,给定其中的一个实体e,计算其与另一个知识图谱中所有实体的距离,最后得到所有训练集实体的排名rank,ranke表示与e对齐的实体的预测排名,Hits@N、MRR的计算方式如下:
其中,Hits@N表示正确实体的排名出现在前N的百分比指标,MRR 是预测结果排名的倒数的平均值。Hits@N与MRR值越大,模型效果越好。
4.4 实验结果
为了验证TEEA的有效性,本文进行了实体对齐预测实验,结果如表2 所示,其中TransEdge[21]的实验结果来自于其论文中,其他基准模型的实验结果均来自于RNM[14]中。在基于翻译的模型中,TransEdge 聚焦于建模知识图谱中的复杂关系,如1-n、n-1、n-n的关系,取得了最好的效果,这说明了关系属性的重要性。在基于图神经网络的模型中,RDGCN、HGCN、NMN、RNM 使用了Glove构造的初始实体嵌入,得到了先进的效果。这说明了考虑实体名称信息能够增强实体对齐的性能。在所有的基准模型中,RNM 在邻域匹配时考虑关系的语义信息与映射属性,取得了最好的效果。在RNM模型中,提出了实体对齐联合关系对齐的迭代框架,实现了实体对齐与关系对齐的互相增强。这说明了实体对齐任务可以联合其他任务,使两者相互增强。在本文中,可以联合实体对齐与三元组对齐,这将在以后的工作中进行研究。
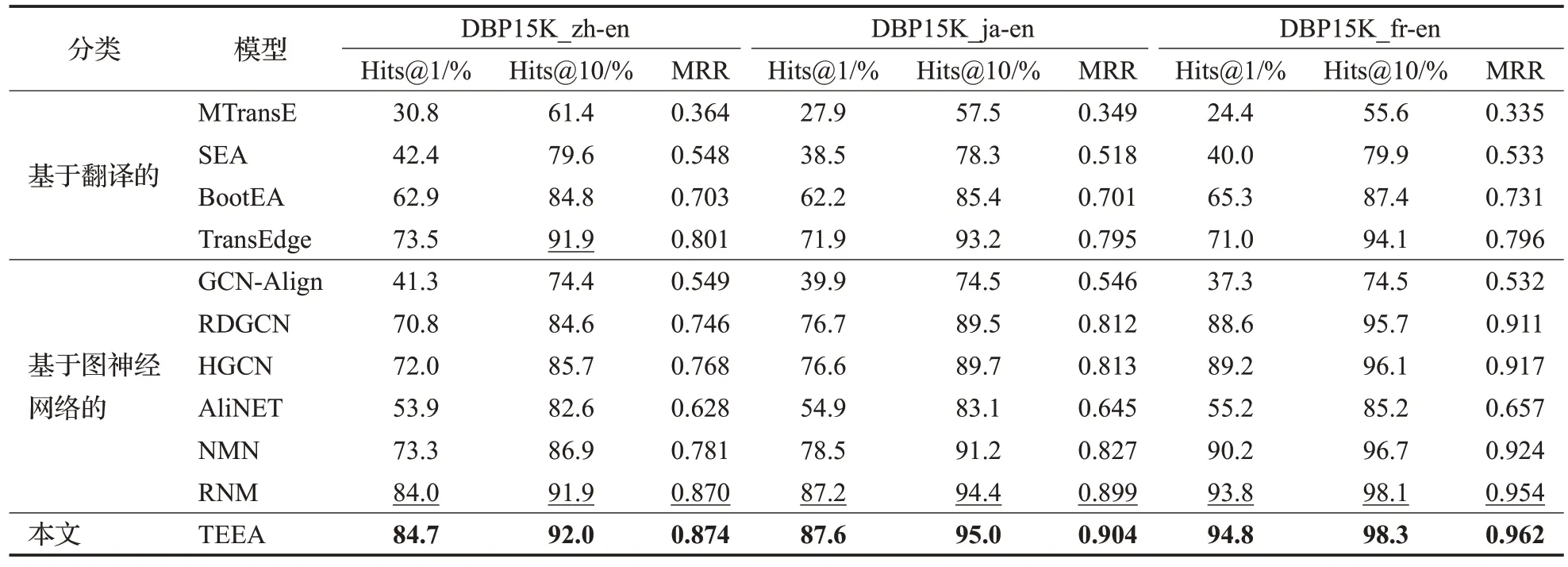
表2 实体对齐实验结果Table 2 Experimental results of entity alignment
本文的模型在三个数据集上的各项指标均取得了最好的结果,这是因为本文的方法通过利用知识图谱中的三元组信息与关系属性信息,能够提高实体对齐的性能。通过观察各个数据集上的Hits@1 与Hits@10 指标,发现Hits@1 指标的提升率高于Hits@10 指标,这说明本文的方法有助于从潜在的实体集合中找出正确的实体,提高实体对齐的命中率。实验结果验证了本文方法对于知识图谱实体对齐是有效的。
4.5 消融研究
为了评估模型TEEA的各个部分的效果,本文进行了消融研究,提供了以下几种TEEA 的变体:TEEA-JE表示不采用三元组嵌入的模型;TEEA-RT 表示不加入关系属性的约束;TEEA-JnoR表示在计算三元组嵌入时不考虑关系属性。此外,考虑到HGCN计算联合嵌入时只拼接了关系,本文添加了一种变体,TEEA-OR表示只拼接关系作为联合嵌入(即不使用公式(10))。实验结果如表3所示。观察各个变体的实验数据,发现这些变体均取得了较好的实验结果,这是因为TEEA 使用了RNM中的迭代模块,从而提高了模型的效果。

表3 消融研究实验结果Table 3 Experimental results of ablation studies
通过比较TEEA-JE与TEEA的实验结果,TEEA-JE在三个数据集的Hits@1、MRR 指标均有了较大的下降。这说明了TEEA 通过使用三元组嵌入进行实体对齐,学习到了知识图谱中的三元组信息,从而提升了实体对齐的性能。
观察TEEA-RT 与TEEA-JnoR 的实验结果,发现实验数据相比于TEEA都降低了,但是各项指标只下降了0.1个百分点左右。这可能是因为知识图谱中的关系属性较为复杂,而本文对关系属性的划分不够精确,同时没有考虑这些关系属性中噪声的影响,使得使用关系属性带来的正面效果可能与负面效果持平,因此这些变体的实验结果与TEEA相差不大。在未来的研究中,将考虑如何更加有效地学习关系属性信息。
通过对比TEEA-OR 与TEEA,TEEA-OR 的各项实验数据均有了较大的下降。这是使用三元组嵌入得到的性能提升,验证了本文利用三元组的方法的有效性。
4.6 关系对齐研究
为了评估关系类型对模型TEEA的影响,本文使用公式(6)生成的关系嵌入进行关系对齐实验,实验结果如表4所示。其中RNM[14]的实验数据来自于其论文中,其余的实验数据来自于HGCN[13]中。模型中-PR表示与HGCN 一样使用实体嵌入近似关系嵌入;-JR 表示联合学习实体与关系嵌入。
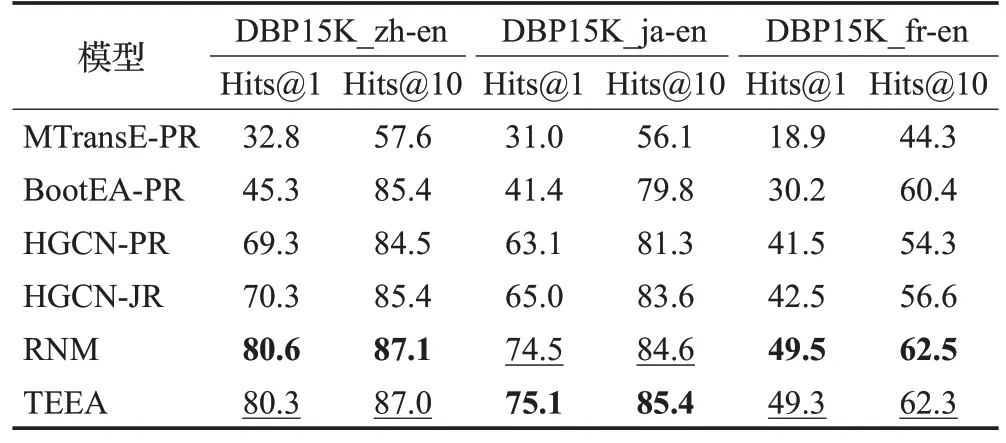
表4 关系对齐实验结果Table 4 Experimental results of relation alignment 单位:%
HGCN 联合实体与关系嵌入,取得了较好的结果。RNM在对齐关系时考虑了头、尾实体的信息,在数据集DBP15K_zh-en与DBP15K_fr-en上取得了最好的结果,这说明关系与它的头、尾实体密切相关。TEEA在数据集DBP15K_ja-en 上取得了最好的结果,其余数据集上取得了次佳的结果,并且所有的实验结果都与RNM 差距不大。这可能是因为两个知识图谱中等价的关系其相连的实体数都不相同,使用关系周围的实体数表示关系类型会引入噪声,从而影响关系对齐的结果。
5 结论与展望
本文提出了基于三元组嵌入的实体对齐方法,旨在学习知识图谱中的三元组信息与关系属性信息。考虑到知识图谱中包含有多种关系属性,本文加入了基于关系属性的约束。在计算实体的三元组嵌入时,本文提出了基于关系属性的计算方法,以得到更加准确的嵌入表示。在公开的数据集上评估本文的模型,并与其他模型对比。实验结果表明本文的模型URAEA 取得了最好的效果,证明了本文方法的有效性。但在包含属性的知识图谱中,提出的模型仍有提升空间,未来将考虑计算属性三元组的嵌入,以适用于包含属性信息的知识图谱。同时,TEEA模型在处理关系属性时也存在一些不足,如没有抑制关系属性中的噪声,在未来的研究中,将考虑更准确地表示关系属性,减少噪声影响,提高对关系属性的学习能力。

