Hot-deformation kinetics analysis and extrusion parameter optimization of a dilute rare-earth free magnesium alloy

Qinghng Wng ,Howi Zhi ,Zhoyng Jin ,Junji H ,Qin Yng ,Wnjun Liu ,Yulong Li,Dolun Chn

a School of Mechanical Engineering, Yangzhou University, No.196 West Huayang Road, Hangjiang, Yangzhou, 225127, China

b School of Materials and Energy, Yunnan University, Kunming, 650599, China

cChangan Auto Global R&D Center, Chongqing, 401120, China

d College of Materials Science and Engineering, Chongqing University of Technology, Chongqing, 400054, China

e Department of Mechanical and Industrial Engineering, Toronto Metropolitan University (formerly Ryerson University), Toronto, ON M5B 2K3, Canada

Abstract The fundamental research on thermo-mechanical conditions provides an experimental basis for high-performance Mg-Al-Ca-Mn alloys.However,there is a lack of systematical investigation for this series alloys on the hot-deformation kinetics and extrusion parameter optimization.Here,the flow behavior,constitutive model,dynamic recrystallization (DRX) kinetic model and processing map of a dilute rare-earth free Mg-1.3Al-0.4Ca-0.4Mn (AXM100,wt.%) alloy were studied under different hot-compressive conditions.In addition,the extrusion parameter optimization of this alloy was performed based on the hot-processing map.The results showed that the conventional Arrhenius-type strain-related constitutive model only worked well for the flow curves at high temperatures and low strain rates.In comparison,using the machine learning assisted model (support vector regression,SVR) could effectively improve the accuracy between the predicted and experimental values.The DRX kinetic model was established,and a typical necklace-shaped structure preferentially occurred at the original grain boundaries and the second phases.The DRX nucleation weakened the texture intensity,and the further growth caused the more scattered basal texture.The hot-processing maps at different strains were also measured and the optimal hot-processing range could be confirmed at the deformation temperatures of 600～723 K and the strain rates of 0.018～0.563 s-1.Based on the optimum hot-processing range,a suitable extrusion parameter was considered as 603 K and 0.1 mm/s and the as-extruded alloy in this parameter exhibited a good strengthductility synergy (yield strength of～232.1 MPa,ultimate strength of～278.2 MPa and elongation-to-failure of～20.1%).Finally,the strengthening-plasticizing mechanisms and the relationships between the DRXed grain size,yield strength and extrusion parameters were analyzed.

Keywords: Mg-Al-Ca-Mn alloy;Constitutive model;Dynamic recrystallization kinetic model;Extrusion parameter optimization;Strengthening-plasticizing mechanisms.

1.Introduction

Room-temperature (RT) strength-ductility trade-off dilemma in magnesium (Mg) alloys is a troublesome problem that needs to be solved urgently [1,2].In the past decade,massive studies have attempted to use rare-earth(RE) alloying method [3,4]and severe plastic deformation techniques [5]to overcome this issue.However,the high cost of production and the complexity of technological procedure to a large extent restrict the industrial applications of Mg alloys.Therefore,the development of low-cost and high-performance Mg alloys containing low RE content,even RE-free Mg alloys,is urgent demand.

The efforts in the reduction of RE content with the addition of other elements such as Al,i.e.,Mg-4.8Gd-1.2Al-1Zn (wt.%) [6,7]and Mg-5Nd-3Al (wt.%) [8],have been widely reported.The interaction between Al and RE not only can produce thermostable intermetallic compounds resistancing grain coarsening,but also acts as effective grain nucleation sites,for enhancing the mechanical properties.Recently,Mg-Al-Ca-Mn alloy series are becoming potential as a new generation of RE-free wrought Mg alloys.An extraordinary high-strength extruded Mg-3.6Al-3.3Ca-0.4Mn (wt.%) alloy was developed,and it exhibited a tensile yield strength (TYS)of～410 MPa and an elongation (EL) of～5.6% [9].The similar mechanical properties were also obtained in an extruded Mg-5.5Al-3.0Ca-0.3Mn (wt.%) alloy [10].Such a high strength was derived from nano-sized Al2Ca or Mg2Ca precipitates and a strong basal texture feature.However,the obviously low ductility of these high-content alloys tends to restrict the potential in industrial applications.The development of the high strong and ductile dilute Mg-Al-Ca-Mn alloys is launched due to excellent extrudablity and rapid aging response.For example,Nakata et al.developed a series of dilute extruded Mg-Al-Ca-Mn alloys,i.e.,Mg-0.3Al-0.2Ca-0.5Mn(wt.%) [11,12],Mg-0.3Al-0.3Ca-0.4Mn (wt.%) [13]and Mg-1.3Al-0.3Ca-0.4Mn (wt.%) [14],which showed a high RT tensile yield strength (beyond 200 MPa) and elongation-tofailure (over 20%) synergy effect by low-temperature highspeed extrusion and subsequent aging,since a high number density of monolayer Guinier Preston (G.P.) zones and fine dynamically recrystallized (DRXed) grains with weak texture components occurred.Liu et al.[15]revealed that a dilute Mg-0.7Al-0.3Ca-0.5Mn (wt.%) alloy subjected to mediumtemperature low-speed extrusion and subsequent T6 aging exhibited a higher TYS of～248 MPa without the loss of EL of～21%.The balance between strength and ductility was mainly attributed to tremendous nano-sizedβ-Mn precipitates,a large number of mono-layered G.P.zones as well as planar Al2Ca phases,and the fully recrystallized fine grains with weak basal texture.The fundamental research on thermo-mechanical conditions provides an experimental basis for high-performance Mg-Al-Ca-Mn alloys.However,there is a lack of systematical investigation on the hot-deformation kinetics of Mg-Al-Ca-Mn alloys.It is of the utmost importance to establish an overall understanding of hot-deformation behavior to determine the optimal hot processing parameters and to obtain the desirable mechanical properties for Mg-Al-Ca-Mn alloys.

Regarding the constitutive equations for modeling and prediction of hot flow stress,the reports on the Arrhenius model,DRX/DRV kinetics models (DRV represents dynamic recovery),Johnson-Cook equation and Fields-Backofen formula have been widely presented in austenitic stainless steels,highentropy alloys and aluminum alloys [16,17].The Arrheniustype constitutive model is a phenomenological one commonly used in the descriptions of hot-deformation behavior of Mg alloys,based on the data between strains and flow stresses under different hot-deformation conditions (temperature and strain rate).Using this model has successfully predicted the hot-deformed microstructures and optimized the hot processing parameters of Mg-2.5Zn-2.5Y-1Mn (wt.%) [18]and Mg-5Zn-3.5Sn-1Mn-0.5Ca-0.5Cu (wt.%) [19]alloys.However,the complex non-linear dependence of flow characteristics(such as deformation temperature,strain rate,strain,etc.)makes the accurate description of hot-deformation behavior become difficult by means of the conventional regression method [20].Machine learning tools,such as artificial neural network (ANN) and support vector regression (SVR),have exhibited its capability of dealing with non-linear predictions in the materials science areas,such as materials design and mechanical properties [21–23].It has been broadly reported that the ANN model had better predictability than the conventional constitutive ones for the flow behaviors of steels,Ti alloys and Mg alloys [20,24-27].For example,Ge et al.[25]revealed that in the study of hot-deformation behavior of high Nb-containing TiAl alloy,the average absolute relative error (AARE) and correlation coefficient (R) utilized to assess the precision of the constitutive model were～1.28%and～0.9998,respectively,by the back propagation (BP) neural network as the most widely used ANN model.Also,Wang et al.[20]pointed out that the AARE value was decreased significantly from～10.33 to～1.43%,and the R value was increased remarkably from～0.9763 to～0.9993 through utilizing the BP neural network,compared with the conventional constitutive mode.To the best of our knowledge,except for the ANN model,other machine learning tools (such as SVR)have not yet been employed to predict the hot-deformation behaviors of Mg alloys.

The hot flow behaviors of Mg alloys are closely related to the DRX process,since they have finite slip systems and low staking fault energy [28].Based on the different hotdeformation conditions,the progress of DRX is usually modeled by the Avrami-type equation and the DRX kinetics can be expressed as a function of the Zener-Hollomon (Z) parameter.Li et al.[29]investigated the relations among the Z parameter,DRX fraction and deformation degree during the hot-compression of Mg-5.8Zn-0.5Zr-1.0Yb (wt.%) alloy.They highlighted that considering the robustness and efficiency of DRX,the deformation regime with the lnZ value less than 24 was preferable.Also,according to the work of Hao et al.[18],a good surface quality and excellent mechanical properties for the extruded Mg-2.5Zn-2.5Y-1Mn (wt.%)alloy could be achieved by the DRX kinetics model and the processing map to optimize deformation parameters.Similarly,Xu et al.[30]established a physically-based DRX model,and this model was imported into the finite element analysis software to predict the evolution of internal state variables (i.e.,dislocation density,grain size and DRX fraction) of Mg-6Gd-5Y-0.3Zr (wt.%) alloy during the extrusion process.

Therefore,in this work,a dilute RE-free Mg-Al-Ca-Mn alloy was prepared,and to study the hot-deformation behavior of this alloy,a series of compressive deformation tests were conducted at deformation temperatures of 573,623,673 and 723 K and strain rates of 0.001,0.01,0.1 and 1 s-1.The strain-related Arrhenius-type constitutive model of the investigated alloy was established.To improve the prediction accuracy of flow stresses at different deformation conditions,the SVR-assisted constitutive model was firstly proposed.Additionally,the DRX kinetics was also systematically studied to unveil the microstructural characteristics (i.e.,DRX fraction and grain size) during the hot-compression.Finally,under the help of processing map,optimizing the deformation parameter aimed to obtain the excellent strength-ductility synergy of a dilute Mg-Al-Ca-Mn alloy in as-extruded state.

2.Materials and methods

2.1. Material preparation

The as-cast Mg-Al-Ca-Mn alloy was prepared in an electric resistance furnace under the atmosphere of SF6and CO2mixed gas (mixing volume ratio was 1:99).The materials used in this study were commercial pure Mg ingot(≥99.99%),pure Al (≥99.9%),Mg-25Ca (wt.%) and Mg-10Mn (wt.%) master alloys.The melt was held at 993 K for 20 min after alloying elements were dissolved into the Mg matrix,and then it was poured into a steel mold of Ф80 × 200 mm in size (diameter × height),which was preheated to 623 K for 1 h The chemical composition of ascast Mg-Al-Ca-Mn alloy was measured by inductively coupled plasma-atomic emission spectroscopy (ICP-AES) and the result shows that the real chemical compositions of the investigated alloys are Mg-1.3Al-0.4Ca-0.4Mn (AXM100).The as-cast AXM100 alloy was solid-solution treated at 723 K for 12 h,and subsequently it was machined into two types of samples with Ф8 × 12 mm in size for the hotcompression and Ф80 × 80 mm in size for the hot-extrusion,respectively.

2.2. Hot-compression and extrusion experiments

Hot-compression tests were performed on a Gleeble-3500 thermo-mechanical simulator at temperatures of 573,623,673 and 723 K and strain rates of 0.001,0.01,0.1 and 1 s-1.Each group was prepared for three samples to ensure the accuracy of experiments.Three extrusion processes were carried out on an XJ-500 horizontal extruder at 603,643 and 683 K with an extrusion ratio of 30:1 and a ram speed of 0.1,0.2 and 1.0 mm/s,respectively.The as-extruded bars were 16 mm in the diameter.

2.3. Microstructural observation and mechanical performance testing

The microstructure of AXM100 alloy in solid-solution treated state could be observed by scanning electron microscopy (SEM,Gemini SEM 300) equipped with energy dispersive spectrometer (EDS).X-ray diffraction (XRD,Rigaku D/Max 2500) was also used to identify the phase constitutions of AXM100 alloy in solid-solution treated state.The microstructural observation and micro-texture analysis of AXM100 alloy in hot-compressive state was performed by electron backscattered diffraction (EBSD,JEOL JSM-7800F)technique.EBSD preparation consisted of grinding on SiC papers of grit sizes of 280,400,600,800,1000 and 1200#,washing,blow-drying as well as electro-polishing at a voltage of 20 V and an electric current of 0.03 A for 90 s at a temperature of-25 °C with a special electrolyte named as AC2.The step size of EBSD scan was set as 0.1 μm.All EBSD data were analyzed using channel 5 software.The average grain sizes of all samples were measured by image-pro plus software.The microstructures and micro-textures of AXM100 alloys in three as-extruded states were characterized by optical microscopy (OM,ZEISS Axiovert 40 MAT) and EBSD.Both SEM and transmission electron microscopy (TEM,FEI TECNAI G2 F20) were used to better observe the second phases of as-extruded alloys.The foils for TEM observations were prepared by mechanical polishing to 50 μm and then punched into disks of 3 mm in diameter.Subsequently,the treated foils were further thinned to 30 nm in thickness by ion beam using GATAN,PIPS 691 device.Tensile mechanical properties of AXM100 alloys in three as-extruded states were measured using the CMT6305–300 KN universal tensile testing machine at a strain rate of 1.2 × 10-3s-1at RT.Each tensile test was performed for three times to guarantee the accuracy of experiments.

3.Results and discussion

3.1. Flow behavior during the hot-compression

Fig.1a exhibits the SEM image of the solid-solution treated AXM100 alloy.A small amount of bright networkshaped second phases embedded into the Mg matrix.By the SEM-EDS result in Fig.1b,the network-shaped phase (points A and B)is mainly composed of three elements of Mg,Al and Ca,which may be considered as (Mg,Al)2Ca phase [15,31].However,the view of SEM mapping reflects a different result that Al and Ca elements are found as the main constituents of the network-shaped phase,rather than Mg element(see Fig.1c and e).According to the report of Suzuki et al.[32],the crystal structure of an eutectic (Mg,Al)2Ca phase in as-cast Mg-4.5Al-3.0Ca-0.1Sr-0.3Mn (wt.%) alloy could be transformed into Al2Ca phase during annealing at 573 K.Therefore,we believe that the network-shaped phase is regarded as Al2Ca phase in the solid-solution treated AXM100 alloy.To further confirm the phase compositions of the solidsolution treated AXM100 alloy,XRD test was performed and its result shows two kinds of feature diffraction peaks withα-Mg,and Al2Ca phases in Fig.1f.However,the diffraction peak intensities of Al2Ca phase are weak,due to the low volume fraction.

Fig.1.(a) SEM observation of the solid-solution treated AXM100 alloy including points A and B scanning results;(b-d) SEM mapping results containing Mg,Al and Ca elements from the area of dotted box in (a);(e) XRD result of the solid-solution treated AXM100 alloy.

Fig.2 shows that the true compressive stress-strain curves of AXM100 alloy at designed deformation temperatures and strain rates.The flow stress of each curve increases sharply and reaches the peak at a low strain,and subsequently it gradually decreases to a relatively steady state.Before reaching the peak stress,the rapid accumulation of dislocations forms the obvious work hardening.When the compressive strain overtakes the critical strain the DRX occurs,the annihilation of dislocations results in the decrease of flow stress via the formation of DRXed grains.This is the so-called dynamic softening effect [18-20,29,30,33].As the work hardening and the dynamic softening attain a dynamic balance,a steady-state flow behavior can be expected.Comparing the true stressstrain curves under different deformation conditions,it can be seen that the peak flow stress and the strain corresponding peak flow stress are sensitive to the deformation temperature and strain rate,as shown in Fig.3.At the same strain rate,the peak flow stress gradually decreases with increasing deformation temperature.For example,the peak flow stress decreases from 83.8 to 16.8 MPa with the deformation temperature from 573 to 723 K at 0.001 s-1(see Fig.3a).This can be attributed to the decreased critical resolved shear stress(CRSS) for non-basal slips and the easy occurrence of DRX[34].In addition,the peak flow stress increases as the strain rate increases at a given temperature.For instance,the peak flow stress increases from 83.8 to 141.7 MPa with increasing strain rate from 0.001 to 1 s-1at the temperature of 573 K(see Fig.3a).At a high strain rate,no sufficient time for energy accumulation and dislocation annihilation results in the lower DRX rate and the higher dislocation density,thereby making the higher flow stress [35,36].On the other hand,there is the same tendency for the strain corresponding peak flow stress,as shown Fig.3b: 1) with increasing deformation temperature from 573 to 723 K,it decreases from 0.165 to 0.090 at 0.001 s-1;2) as the strain rate increased from 0.001 to 1 s-1,it increases from 0.165 to 0.220 at 573 K.This means the work hardening stage is shortened with the increase of deformation temperature or the decrease of strain rate,which is also closely related to the accelerated DRX process.

Fig.2.True compressive stress-strain curves of the investigated alloy at designed deformation temperatures and strain rates.

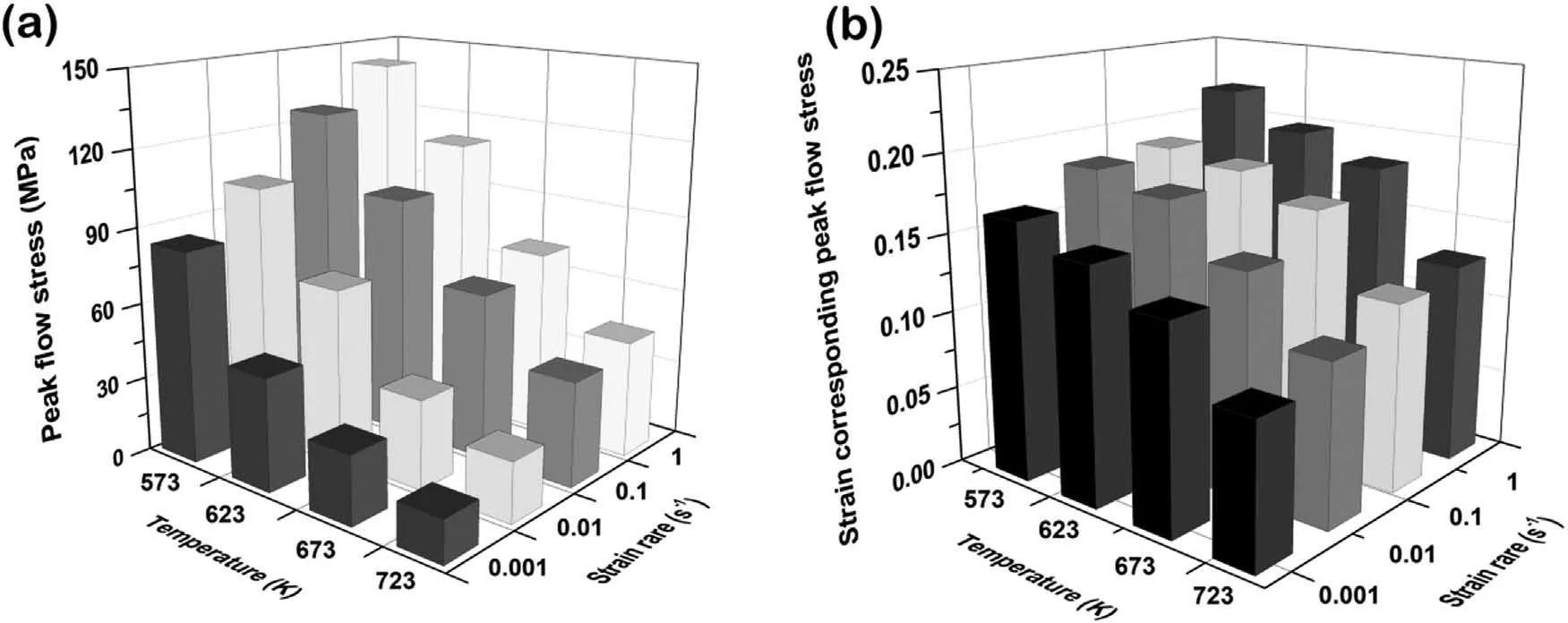
Fig.3.(a) Peak flow stresses and (b) strains corresponding peak flow stresses of the investigated alloy at designed deformation temperatures and strain rates.

3.2. Constitutive model during the hot-compression

The conventional constitutive models can be established using the Arrhenius equations as follows [37]:

Eqs.(1 and 2) are usually used as the constitutive models at a low stress and high stress levels,respectively.At the whole range of stress,the constitutive model can be described by Eq.(3),which is employed in this work.

In general,the strain rate and deformation temperature can be expressed as a function of Zener-Hollomon parameter (Z)as follows [38]:

Combining Eq.(3)with Eq.(5),Eq.(6)is given as follows:

Thus,the functional relation of the flow stressσand theZparameter is shown as follows [20]:

Combining Eq.(5) with Eq.(7),the converted constitutive model can be described and the related material constantsα,Q,nandAneed to be calculated.As a special case,these material constants under the condition of strain of 0.2 can be calculated by Eqs.(8-12).

Take natural logarithms of both sides of Eqs.(1 and 2),and the following relationship can be obtained:

Thelnis as a function oflnσandσ,shown in Fig.4a and b,respectively.The averagen1andβvalues can be deemed as the slopes of these two figures,～9.188 and～0.131,respectively.Together with Eq.(4),theαcan be calculated as～0.014.

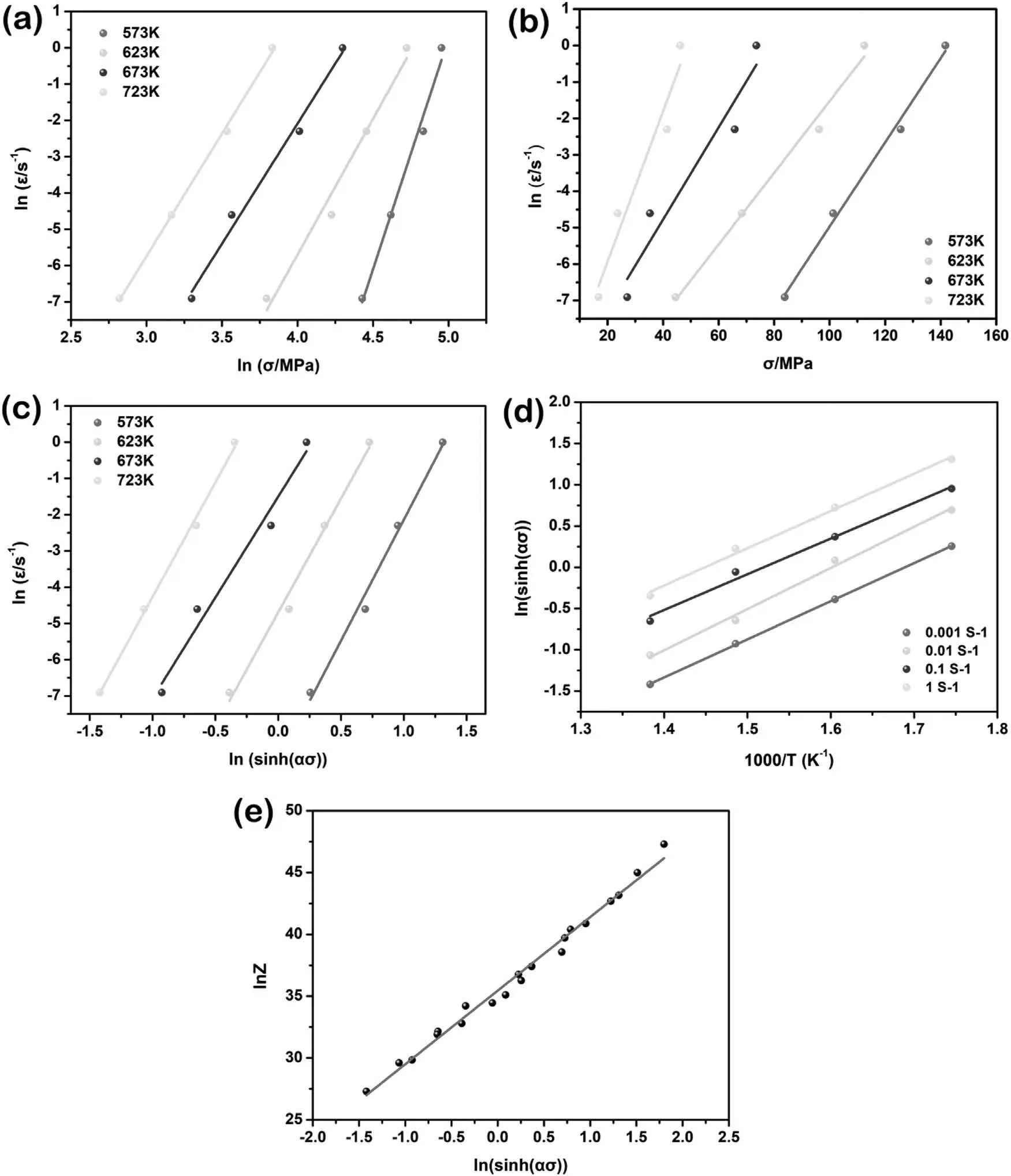
Fig.4.Linear relations of (a) ln -lnσp;(b) ln -σp;(c) ln -ln[sinh(ασp)];(d) ln[sinh(ασ)]-1/T and (e) lnZ- ln[sinh(ασp)]under the peak flow stress condition.

Take natural logarithms of both sides of Eq.(3),and the following relationship can be expressed:

The linear relation ofln-ln[sinh(ασ)]is described in Fig.4c,and the averagenvalue is obtained by the slope of this linear relation,～6.210.

In order to get the value ofQ,take partial derivatives of both sides of Eq.(10) can be presented as follow:

The average s value (～ 3.987) is the slope of ln[sinh(ασ)]-1/Trelation,as shown in Fig.4d.Therefore,theQvalue at the strain of 0.2 is about 205.7 kJ/mol,larger than the activation energy for the self-diffusion of pure Mg (～135 kJ/mol [39]).The highQvalue means the low deformability of alloy during the hot-compression.Xie et al.[40]reported that the nano-clusters enriched in Al and Ca atoms,along the dislocations,could be found at the early stage of extrusion.The existing dislocations would exhibit a higher thermal stability by the segregation of these nanoclusters,which strongly reduced the rate of dynamic recovery and recrystallization.In addition,Mn element tends to be in a form ofα-Mn particles to a large extent pinning the original grain boundaries in the deformed Mg alloys containing Mn to restrain the DRX [41,42].Therefore,we reasonably believe that the occurrence of these nano-scale phases enhances the hot-deformed resistance,giving rise to the highQvalue in AXM100 alloy.

To obtain the constantA,take natural logarithms of both sides of Eq.(6) and the following relationship is shown:

According to Eq.(5),combined with the calculated result ofQvalue,theZvalues at different deformation conditions are obtained.Fig.4e shows the linear relation oflnZ-ln[sinh(ασ)].ThelnA(～35.452) is considered as the intercept on ordinate.Based on the above calculation,all the related material constantsα,Q,nandAcan be obtained to establish the constitutive model at the strain of 0.2.

In order to accurately describe the constitutive model during the whole hot-compression,the parameters ofα,Q,nandAare necessary to be treated as functions of the strain.Fig.5 shows the relationship between these related parameters and the strain.They can be fitted by using 5-order polynomial equations as follows:

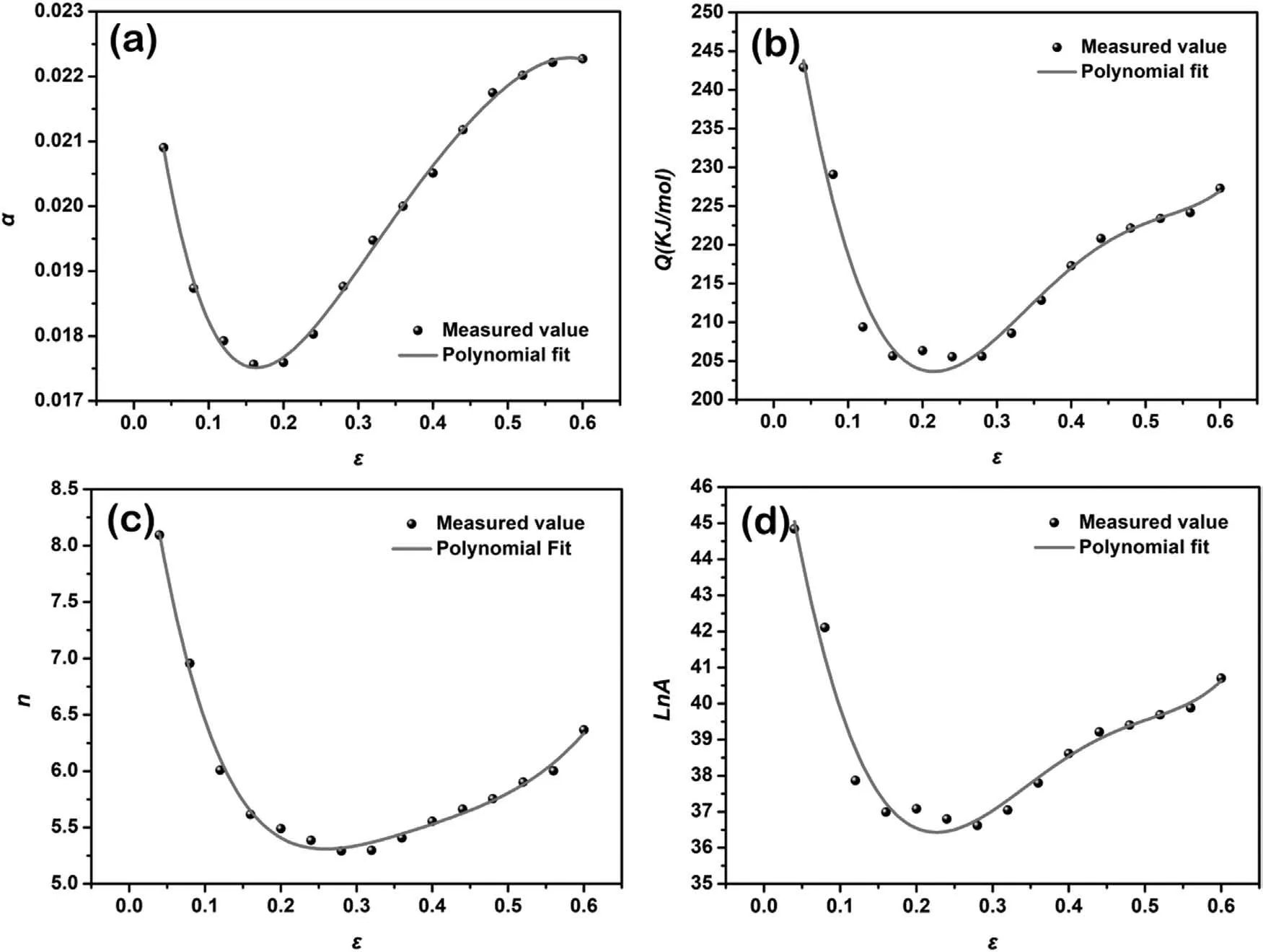
Fig.5.Relationships between (a) α,(b) Q,(c) n and (d) lnA and the true strain ε by 5-order polynomial equations.

whereεis the strain.The values of the coefficientsα0-α5,Q0-Q5,n0-n5andA0-A5are listed in Table 1.The strain-related constitutive model of AXM100 alloy is established and a comparison between the predicted stresses and the experimental results under different strain rates is shown in Fig.6a-d.As seen,the conventional Arrehenius model is effectively suitable for the flow curves under the low strain rate and high temperature,especially for 0.001 s-1and 723 K.Although the trend of each flow curve can be described,there exist still obvious derivation between the predicted and the experimental data.The predictability of the models was evaluated by the R and the AARE.The R represented the strength of the linear relationship between the experimental and predicted values.The AARE was calculated to provide additional unbiased statistical analysis of the predictability of the model.They are defined as follows[20,25]:

Table 1Coefficients in the polynomial fitting of α, Q, n and A for the constitutive model of the investigated alloy.

Fig.6.Comparison of experimental flow curves and predicted results of conventional Arrehenius and SVR constitutive models under different strain rates: (a,e) 0.001 s-1;(b,f) 0.01 s-1;(c,g) 0.1 s-1;(d,h) 1 s-1.

wherenis the size of flow stress set,Eiis the value of experimental flow stress and ¯Eis the mean value ofEi,Piis the value of flow stress predicted using constitutive model and ¯Pis the mean value ofPi.It can be seen that even though the R is above～0.98,the AARE is about～11.52%for the conventional Arrehenius model.Further analysis for the model accuracy is investigated by the calculation of the standard deviation (S.D.) of the relative error (δ),which are defined as follows [20]:

The result is shown in Fig.7c,and theS.D.deviated at a large range (～12.35).This indicates that the predictability of the conventional Arrehenius model for the flow stress of AXM100 alloy is unsatisfactory.

Fig.7.Correlation and the standard deviation S.D.between experimental and predicted flow stresses by conventional Arrehenius (a,c) and the SVR (b,d)constitutive models.

To more precisely predict the flow stress during the hotcompression,a novel machine learning tool (SVR with the radial basis function as the kernel function for performing machine learning) was implemented.In the database (1125 datasets),80% of the data were randomly selected to train the model and other 20% to test the performance of the model.We optimized the two hyper-parameters of SVR,cost of making mistakes and gamma controlling the shape of the segmented hyper-plane utilizing the 10-fold cross validation method [43].The flow stress of AXM100 alloy under different deformation conditions is calculated by the SVR constitutive model and compared with the experimental flow curves as shown in Fig.6e-h.The predicted data is much fitted for the experimental flow curves under each strain rate and temperature.The large discrepancies between the experimental data and the calculated results of the conventional model are remarkably reduced.As mentioned above on the error assessment by Eqs.(17-20),we also calculate the relative parameters shown in Fig.7b and d.Compared with the conventional Arrehenius model,the predictability is significantly improved by using the SVR model.The R value increases from～0.9806 to～0.9986;the AARE and S.D.values shapely decrease from～11.5 to～1.23% and from～12.35 to～1.79,respectively.As mentioned above,except for the reported ANN model [20,24-27],the SVR model also shows the higher accuracy,and the predicted flow stresses are well matched with the experimental curves.Based on the data,it is evident that the machine learning approach can be exploited to predict the hot-deformation behavior of Mg alloys.

3.3. DRX kinetics behavior during the hot-compression

The kinetics model of DRX can be described by the Avrami equation as follows [29,44]:

whereXDRXis the volume fraction of the DRXed grains,εcis the critical strain for the occurrence of DRX,ε0.5is the strain for 50% DRX fraction,kDandnDare material constants.Given a constant initial grain size,εcandε0.5are usually expressed by a power-law function of theZparameter as follows [29]:

whereB1,B2,m1andm2are material constants.Ifσcandσ0.5can be obtained under different deformation conditions,the correspondingεcandε0.5are also well measured by true stress-strain curves during hot-compression.Theσccan be gained through analyzing the work hardening rate-stress (θσ) curve.Fig.8a shows an example at 573 K and 0.01 s-1.Theθ-σcurve is divided into three stages: 1) theθdrops sharply to the value ofσ=σc.The saturated stressσsatcan be readily measured in this stage by making extrapolation toθ=0;2) theθreduces continuously 0 (from theσcto the peak stress(σp)in the manner of convex shape).In this stage,the thermal softening mainly becomes increasingly predominant;3) theθdecreases to the minimum value from 0 and then increases to 0 (σss,the steady stress),because the softening effect induced by DRX counteracts working hardening.According to Eq.(24),theσ0.5can be calculated as follows[45]:

Fig.8.(a) Work hardening rate-stress (θ- σ) curve at 573 K and 0.01/s;(b) Linear relationships between lnεc, lnε0.5 and lnZ;(d) ln(-ln((1-(σp- σ)/(σp- σss)))) as a function of ln((ε- εc)/ε0.5).

Based on theθ-σcurves and Eq.(24) under different deformation conditions,theσc,σ0.5,εcandε0.5values are collected and summarized in Table 2.Take natural logarithms of both sides of Eqs.(22 and 23),and the following linear relationship can be shown in Fig.8b and c.TheB1,B2,m1andm2values are estimated and the finalεcandε0.5can be defined as follows:

Table 2Values of σc,σ0.5,εc and ε0.5 of the investigated alloy.

Combining Eq.(21) with Eq.(24),the meankDandnDcan be determined by linear regression (see Fig.8d) under different deformation conditions as follows:

The mean values of thekDandnDcan be calculated as～1.169 and～3.091,respectively.Thus,the DRX kinetics model of AXM100 alloy can be expressed as follows:

According to Eq.(28),theXDRXas a function of theεis shown in Fig.9a.With the increase of theε,theXDRXincreased along an S-shape curve.Under all the deformation conditions,theXDRXcan reach 100%,as theεincreases to 1.At the sameε,theXDRXgradually is low with thelnZ.In other words,the occurrence of DRX is more difficult at the largerlnZ.From the views of temperature and strain rate,with increasing the temperature,theεcorresponding to 100%DRX reduces under the same strain rate;as the strain rate increases,the mentionedεis incremental,as shown in Fig.9b.For instance,at 0.01 s-1,theε(100% DRX) values are ordinarily～0.98,～0.86,～0.78 and～0.70 with the temperature from 573 to 723 K;at 723 K,theε(100% DRX)values are successively～0.66,～0.70,～0.78 and～0.83 with the strain rate from 0.001 to 1 s-1.

Fig.9.(a,b) Predicted DRX volume fraction curves and ε for 100% DRX under different deformation conditions,respectively.

To verify the calculated DRX kinetics model,three deformation conditions (623 K @ 0.1 s-1to theεof 0.4 and 0.6 respectively) are selected and the corresponding microstructures are observed,as shown in Fig.10.With the increase of the strain,the level of DRX gradually becomes high (see Fig.10a and b).The area fraction of these DRXed grains,took out from Fig.10c and d,account for～52 and～87%under the strains of 0.4 and 0.6 shown in Fig.10e and f.This result is consistent with the predicted values of the calculated DRX kinetics model.In addition,we also find the nucleation of these DRXed grains occurs at the original grain boundaries and the Al2Ca second phases in this alloy.Those DRXed grains nucleated preferentially at the grain boundaries have a typical necklace-shaped structure [20,30,46],and the large-sized second phases tend to be in favor of the formation of the DRXed grains via particles stimulate nucleation (PSN)effect [47,48].The unDRXed regions mainly exhibit a strong basal texture component.Under a compressive load,basal slip or twinning is difficult to be activated in the unDRXed region due to deformation“hard”orientation.However,at 623 K,the CRSSs of non-basal slips reduce,likely giving rise to the appearance of non-basal slips that also play a pivotal role in the DRX process after the preferential nucleation mechanisms,i.e.,grain boundary bulging,PSN,and twinning nucleation.Expect for the DRX nucleation,the growth of the DRXed grains also can be observed,and the average sizes of the DRXed grains are～4.3 and～8.5 μm as the strain increases from 0.4 to 0.6 in Fig.10e and f,respectively.Generally,the DRX process not only induces grain refinement,but also generates texture weakening [38,48,49].Compared with the whole region,the area of the DRXed grains for each strain condition shows a low basal texture intensity in (0001) pole figure.As increasing the strain,the DRXed grain growth triggers a weaker basal texture shown in Fig.10g-j.This might be explained as the preferred growth of grains with the special non-basal orientation,since the co-segregation of Al and Ca into grain boundaries hindered the growth of grains with the basal orientation [50].

Fig.10.(a,b) OM images and (c,d) EBSD images of the investigated alloy subjected to hot-compression of 0.4 and 0.6 strains,respectively;(e,f) DRX regions took out from (c) and (d),respectively;(g,h) (0001) pole figures of whole (c) and DRX (e) areas,respectively;(i,j) (0001) pole figures of whole (d)and DRX (f) areas,respectively.CD represents the compressive direction.

3.4. Hot-processing map during the hot-compression

A dynamic material model,established by Prasad et al.[51],was based on the continuum theory of large plastic deformation,irreversible thermodynamics and physical system simulation.In this model,the workpiece was regarded as a power dissipator.The total power dissipated by the workpiece(P) could be divided into the powers (GandJ) dissipated by the plastic deformation and microstructure evolution of the material,respectively.ThePcan be expressed as follows[51]:

The flow stress under a given deformation condition (ε,T)can be expressed as follows [36]:

whereKis a material constant,andmis the strain rate sensitivity coefficient.Combining Eq.(29) with Eq.(30),Jcan be given in Eq.(31) as follows:

When m is considered as 1,Jreaches its maximum value(Jmax=σ/2).The efficiency of power dissipation (η) for nonlinear dissipation can be determined as follows [18]:

In general,a higherηmeans a better workability under this condition,but it may be accompanied with an instability.Therefore,the instability criterion based on the extremum principle was proposed as follows [18,52]:

Combining the power dissipation equation with the instability criterion can be used to determine the hot-processing map of a material containing the instability region.Based on the above analysis,the hot-processing maps of the investigated alloy at the hot-compressive strains of 0.2,0.4 and 0.6 are drawn and shown in Fig.11.The contour numbers represent the power dissipation efficient,and the shaded red regions correspond to the flow instability.At the low strain of 0.2,the flow instability region focuses on an area with medium temperatures (573～623 K) and medium strain rates(0.1～1 s-1),as shown in the top left corner of Fig.11a.With the increase of strain up to 0.4,the flow instability region extends to the temperature of～660 K and the strain rate of～0.05 s-1exhibited in Fig.11b.When the strain reaches 0.6,the mentioned flow instability region continuously amplifies to the temperature of～685 K and the stain rate of～0.03 s-1,and a new flow instability region (with temperatures of 650～720 K and strain rates of 0.001～0.002 s-1)occurs in the bottom right corner of Fig.11c.These results indicate that strain variables have a significant effect on the hot-processing map.As seen in Fig.2,the investigated alloy is basically in a steadily flow state after the strain of 0.6,and thus we can develop an appropriate hot-processing range via Fig.11c.Given a criterion that a good workability corresponds to the high power dissipation area,a suitable hot-processing range can be initially confirmed and shown in the green full lines corresponding to the power dissopation ranged from 0.36～0.46 of Fig.11c.

Fig.11.Hot-processing maps of the investigated alloy under different strains:(a) 0.2;(b) 0.4;(c) 0.6.Note that the shaded red regions represent the flow instability areas,and the region of green full lines shown in (c) is an optimal hot-processing range.

3.5. Analysis of microstructures and mechanical properties of as-extruded alloys

Based on the mentioned optimal hot-processing range,we can draw up a fitted extrusion parameter.It is appropriate to reduce the deformation temperature or improve the strain rate to obtain fine grains at the optimum domains [18,36,53].Therefore,there are three schemes selected at the optimal hot-processing range: 1) 603 K and 0.025 s-1;2) 643 K and 0.056 s-1;3) 683 K and 0.263 s-1,respectively.According to the equation cited in Ref.[54],the relationship between the average strain rate() and extrusion speed (VR) at a given extrusion temperature is expressed as follows:

whereERis the extrusion ratio,DBandDEare the billet and extrudate diameters,respectively.In this work,ER,DBandDEare set as 30:1,80 and 16 mm,respectively.Thus,the mentioned three hot-processing schemes correspond to the following extrusion parameters: 1) 603 K and 0.1 mm/s (case 1);2) 643 K and 0.2 mm/s (case 2);3) 683 K and 1.0 mm/s(case 3),respectively.

Fig.12 shows the microstructures of as-extruded alloys in cases 1,2 and 3.From the OM images of longitudinal sections (Fig.12a,c and e),the complete DRX occurs in case 1 and with the increases of extrusion temperature and speed,the DRXed grains grow accompanied by the formation of the elongated unDRXed grains in cases 2 and 3,especially for case 3 along the extrusion direction (ED).In addition,the average grain sizes grow from～4.8 to～8.9 and～15.2 μm for case 1,2 to 3,respectively.This result is consistent with a large number of reports that decreasing the extrusion temperature and/or speed was beneficial for grain refinement [55–57].As for the EBSD images of cross sections (Fig.12b,d and f),an obvious microstructural inhomogeneity is increasingly severe,since boosting the extrusion temperature and speed intensify the movement of grain boundaries.The co-segregation of Al and Ca elements to the DRXed grain boundaries(shown in Fig.S1 in “Supplementary materials”) effectively impeded their motions guaranteeing a uniform grain growth at a low velocity,but at a high temperature,solute drag-controlled migration transformed to rapid (free) migration (exhibited by large-sized grains) inducing an abnormal grain growth [58].This statement can explain the remarkable microstructural inhomogeneity in case 3 very well.Expect for the observations of grain distribution and size,we also measure the microtextures of as-extruded alloys in three cases.It can be seen that typical basal fiber textures are found in (0001) pole figures for three as-extruded alloys,and ＜10–10＞//ED orientation is preferential from (10–10) pole figure in each case.Under the same test areas,the alloy in case 1 has a weaker texture intensity than in cases 2 and 3,because the DRX process benefits texture weakening.

Fig.12.(a,c,e) OM images from longitudinal sections of as-extruded alloys in cases 1,2 and 3,respectively;(b,d,f) EBSD results from cross sections of as-extruded alloys in cases 1,2 and 3,respectively.

Fig.13 displays the second phases on longitudinal sections of three kinds of as-extruded alloys by SEM.A certain number of granular-shaped second phases with an average size of～40 nm uniformly distribute on the matrix in all cases,as shown in Fig.13a,d and g.The area fractions of these second phases are～0.6,～0.5 and～0.5% in case 1 to 3,respectively.By the SEM-EDS results (see Fig.13b,c,e,f,h,and i),we find that these second phases mainly are made up of two kinds of chemical compositions.Taking case 1 as an example,phases A and B are labeled in Fig.13a by red and green circles,and their element constituents are listed in Fig.13b and c,respectively.As seen,phase A mainly contains Mg(as the matrix element that it can be inevitably measured),Al and Ca elements having an atom ratio (about 2:1) Al and Ca.This phase may be considered as Al2Ca.With respect to phase B,it mainly consists of Mg (as the matrix element),Al and Mn elements,and an atom ratio of Al and Mn is approximately 8:5.Thus this phase can perhaps be deemed as Al8Mn5.In order to further confirm the speculation from the SEM results,Fig.14 provides the TEM observations and the diffraction spots of the selected second phases in case 1.A clear TEM image shows the same findings as the SEM result in terms of the distribution and average size of second phases marked by blue arrows (see Fig.14a).Fig.14b and d exhibit the high resolution TEM images corresponding to two phases labeled by blue arrows 1 and 2 in Fig.14a.From the views of morphologies and sizes,no obvious difference for both two phases.However,the results of diffraction spots from Fast Fourier Transformation (FFT) images indicate that the selected two phases are Al2Ca and Al8Mn5shown in Fig.14c and e,respectively.Nevertheless,Liu et al.[15]pointed out that Mg2Ca,Al2Ca andβ-Mn phases could be formed in an as-extruded Mg-0.7Al-0.3Ca-0.5Mn alloy.We argue that the distinction between Ref.and our work is mainly attributed to alloying composition contents.The more amounts of Al element are enough to preferentially react with Ca and Mn elements to produce Al2Ca and Al8Mn5phases having the lower mixing enthalpy values than Mg2Ca andβ-Mn phases[59,60].Therefore,combining the SEM with the TEM results,we ensure in our work three kinds of as-extruded alloys are mainly composed of Al2Ca and Al8Mn5phases,and all asextruded alloys have a similar phase area fraction of～0.5%and an average phase size of～40 nm.

Fig.13.(a,d,g) SEM images of second phases on longitudinal sections of as-extruded alloys in cases 1,2 and 3,respectively;(b,c) SEM-EDS results of points A and B labeled by red and green circles in (a),respectively;(e,f) SEM-EDS results of points C and D labeled by red and green circles in (d),respectively;(h,i) SEM-EDS results of points E and F labeled by red and green circles in (g),respectively.

Fig.14.(a) TEM image of second phases marked by blue arrows on longitudinal section of as-extruded alloy in cases 1;(b,d) high resolution TEM images corresponding to two phases labeled by blue arrows 1 and 2 in (a),respectively;(c,e) FFT images corresponding to two phases from (b) and (d),respectively.

The tensile true stress-strain curves of as-extruded alloys in three cases are shown in Fig.15a,and the detailed mechanical properties are listed in Table 3.All curves are convex shapes and typical tensile properties (i.e.,yield strength of～232.1 MPa,ultimate strength of～278.2 MPa and elongation-to-failure of～20.1%) in case 1 exceed these in cases 2 and 3,indicating that case 1 is an optimal extrusion parameter among the predicted hot-processing range.Compared with other as-extruded Mg-Al-Ca-Mn series alloys [9-15,31,59],the as-extruded alloy in case 1 also shows a resulting strength-ductility synergy (see Fig.15b).Generally,the mechanical properties of a specific Mg alloy are determined by its microstructure characteristics (i.e.,grain size,texture and second phase).These quantities can indeed also be significantly modified by thermo-mechanical processing,which gives additional degrees of freedom for material researchers to control the microstructure features and further enhance the mechanical properties of alloys.In the following section,the strengthening-plasticizing mechanisms of as-extruded alloys in three cases are analyzed comparatively,and the relationships between the grain size,yield strength and extrusion parameters are established.

Table 3Tensile properties of as-extruded investigated alloys in three cases.

Fig.15.(a) Tensile true stress-strain curves of as-extruded alloys in three cases;(b) relationship of tensile yield strength and elongation-to-failure of the reported as-extruded Mg-Al-Ca-Mn series alloys [9-15,31,59],and comparison with three kinds of as-extruded AXM100 alloys in this work;(c) relationships between lnd, lnσsand lnZ of as-extruded alloys;(d) relationships between theoretical grain size,yield strength and extrusion temperature of as-extruded alloys under a given extrusion speed (1 mm/s).

Strengthening mechanisms

In as-extruded Mg alloys,grain boundary strengthening,texture strengthening,second phase strengthening,solid solution strengthening and dislocation strengthening are common strengthening mechanisms for the yield strength,which is expressed as follows [42,61]:

whereσsis the tensile yield stress,ΔσGBandΔσTare the contributions from grain boundary and grain orientation on the yield stress,respectively,Mis the Taylor factor (～2.5) [62],τ0is the CRSS,Δτss,ΔτpandΔτρare the CRSSs contributed by solid solution strengthening,second phase strengthening and dislocation strengthening,respectively.M(τ0+Δτss) is considered to beσ0that is the intrinsic strength taken which is taken as the as-cast yield strength (～40 MPa in this work) [63],because solid solution strengthening is limited and not obviously changed after extrusion.

TheΔσGBcan be calculated by Hall-petch relationship as follows:

Thekvalue is about 205 MPa/μm2in basal-oriented Mg alloys[64],anddaveis the average grain size.Thus the contributions of grain boundary are～83.9,～61.6 and～47.1 MPa for as-extruded alloys in cases 1,2 and 3,respectively.

Basal slip is a deformation mode most easy to be activated at RT.The low Schmid factor (SF) for basal slip suggests that plastic deformation is so difficult.In other words,reaching the yield strain requires the high yield stress in a low SF alloy.A revised form of Hall-Petch relationship can calculate the effect of texture on the yield stress as follows [42,65]:

Based on the observations of Figs.13 and 14,a certain amount of granular-shaped nano-scale second phases occupy the matrix impeding the motion of dislocations and inducing the second phase strengthening by Orowan law.We consider these granular-shaped phases as approximately a spherical shape of uniform diameter of～40 nm.The Orowan increment on the yield stress produced by the need for dislocations to by-pass these obstacles is given as follows [66]:

whereGis the shear modulus of the Mg matrix phase (～17 GPa),bis the magnitude of the Burgers vector of the slip dislocations (～0.32 nm),vis the ratio of Poisson (～0.3),andfpis the area fraction of nano-scale second phases.The calculated results show that all the second phase strengthening values are～34.1 MPa for as-extruded alloys in three cases.

In addition,the residual dislocations in the unDRXed regions can exert an indispensable impact on the yield stress during tension by the dislocation strengthening (Δσρ),which is evaluated as follows [67]:

whereαis the contant (～0.2),andρGNDis the geometrically necessary dislocation density.During extrusion,most of grains release the stress via the DRX,while for the un-DRXed regions they can accommodate the strain through the residual dislocations that are known as the geometrically necessary dislocations (GNDs).Based on the EBSD data,the averageρGNDvalues for the unDRXed regions are～1.3,～3.3,～10.1 (× 1014)m-2 for as-extruded alloys in cases 1,2 and 3,respectively.So,the corresponding effect of residual dislocations on the yield stress is～1.2,～3.5 and～10.5 MPa.In conclusion,the calculated total contributions by different strengthening mechanisms are～229.7,～192.1 and～177.5 MPa for as-extruded alloys in cases 1,2 and 3,respectively.The maximum errors between the predicted and the experimental yield stress values are～0.9,～0.5 and～3.6% for three cases,indicating that the analysis of strengthening mechanisms for as-extruded alloys is fairly suitable.

Plasticizing mechanisms

Compared with the mentioned strengthening mechanisms,plasticizing mechanisms are difficult to be calculated quantitatively.As a result,we discuss qualitatively the factors to affect the ductility of three kinds of as-extruded alloys in this section.It is well known that the following aspects (i.e.,grain size,texture,second phase,non-basal slip and twinning) play significantly pivotal roles on the ductility of Mg alloys.

Refining the grain size is an effective approach to improve simultaneously the strength and ductility of Mg alloys.When the metallic material is applied to an external force,the plastic deformation of grains accommodates the macroscopic strains.The greater the amount of grains is,the stronger the ability to coordinate the macroscopic strain gets,together with the lower level of stress concentration.Therefore,the fine-grained materials show the higher ductility than the coarse-grained ones [68].Our result is very consistent with this classical law.The fine-grained as-extruded alloy in case 1 exhibits a higher elongation-to-failure than other as-extruded alloys with the coarse average grain sizes in cases 2 and 3.

Texture,as an important feature,strongly influences the mechanical properties of Mg alloys.In the “strengthening mechanisms” section,we calculate its contribution on the yield stress,and argue that the basal-oriented as-extruded alloys in three cases have an obvious texture strengthening effect due to the low SFs for basal slip.According to a large number of reports [69,70],the SF for basal slip is proportional to the ductility of Mg alloys at RT.Namely,a lower SF alloy tends to show a lower ductility.In this work,three kinds of as-extruded alloys have a similar SF for basal slip,and thus they,in theory,should display little difference in the elongation-to-failure.Nevertheless,the fact is not this relation(see Table 3),evidently meaning that texture is not a main factor to make the ductility of as-extruded alloys in three cases different.

In the particle-containing materials,the void formation at second phase particles may attribute to a fracture.Based on the report of Huang et al.[71],a critical stress for the void nucleation is proportional to ther-1/2(rpresents the average radius of spherical particles).This suggests that the occurrence of voids needs a larger stress in the materials with finer particles.A small particle size minimizes the possibility for multiple slip-band pileups that increase the local stress and create the fracture.In this work,most of fine nano-scale second phase particles can be observed and distribute on the matrix for three kinds of as-extruded alloys.Thus,the effect of second phase on worsening the ductility can be ignored.

In Mg alloys containing some specific elements,i.e.,RE,Ca and Li,non-basal slips can be activated at RT when the alloys are applied to plastic deformation,since these elements solutioned into the matrix effectively reduced the stacking fault energy and the ratio between CRSSs of non-basal and basal slips to produce non-basal dislocations.The non-basal slip activation provides an extra slip system to better coordinate the external strains,guaranteeing a high work-hardening capacity.As reported by Sandlöbes et al.[72],the tiny doping with Al and Ca gave rise to a huge macroscopic effect on the ductility by activating in addition to basal also pyramidal slip.However,in this work,we hardly ever find the appearance of non-basal slip in as-extruded alloys after a certain of tensile strain at RT.Taking case 1 as an example,Fig.S2 (see in “Supplementary materials”) shows the bright field TEM images of as-extruded alloy in case 1 observed under two-beam diffractions after tension of～8%.Based on theg·b=0 invisible criterion,no any dislocations can be found underg=0002 condition shown in Fig.S2a,indicating that there are not non-basal dislocations activated during tension.On the contrary,the straight dislocation lines (labeled by red arrows) parallel to the (0002) plane are treated as a result of basal dislocations underg=10–10 condition (see Fig.S2b).These results suggest that in this work the ductility of three kinds of as-extruded alloys have no connection with non-basal slips.

Expect for the mentioned above,twinning is also an important factor to influence the ductility of Mg alloys.the work of Barnett [73,74]revealed {10–12} extension twinning is in favor of the ductility of alloy during deformation,while{10–11} contraction twins and/or {10–11}-{10–12} double twins might be responsible for decreasing an uniform elongation because of the generation of local twin-sized voids in these twin boundaries having an obvious stress concentration.These contraction twins and double twins,as the sources of micro-cracks,easily occur in the coarse-grained alloys with a strong basal texture inducing the preferential fracture,when they suffer from tension along the ED [75].Therefore,in this work,the coarse-grained as-extruded alloy in case 3,accompanied by amounts of unDRXed regions,has a terrible elongation-to-failure probably as another result of the formation of contraction twins and/or double twins,in addition to grain coarsening effect.

Relationships between the grain size,yield strength and extrusion parameters

As we know,the relationship between the average DRXed grain size (dDRX) and Z parameter defined in some earlier studies as follows [29,38]:

whereCandiare material constants.Take natural logarithms of both sides of Eq.(40),and the following relationship is shown as follows:

Fig.15c,marked by navy color line,plots the linear relationship betweenlndDRXandlnZof as-extruded alloys in three cases,and it is expressed as follows:

Combining Eqs.(5),(34) with (42),we can obtain a modified relation at a given extrusion speed,i.e.,VR=1 mm/s,as follows:

When the investigated alloy is extruded under different extrusion temperatures (573～723 K),its theoretical DRXed grain sizes can be predicted by Eq.(43) shown in Fig.15d marked by navy color line.It can be clearly seen that with the increase of extrusion temperature,the theoretical DRXed grain size gradually increases exponentially.

Based on the a modified Hall-petch relation(lnσs∝lndDRX),we can speculatelnσsmay be also as a function oflnZ.Through data fitting,there is a linear relationship betweenlnσsandlnZexhibited in Fig.15c,labeled by wine color line.This linear equation is expressed as follows:

Also,combining Eqs.(5),(34) with (44),we can obtain a modified relation at a given extrusion speed,i.e.,VR=1 mm/s,as follows:

When the investigated alloy is extruded under different extrusion temperatures (573～723 K),its theoretical yield strength values can be predicted by Eq.(45)shown in Fig.15d marked by wine color line.As seen,with the increase of extrusion temperature,the theoretical yield strength remarkably reduces.In conclusion,According to the relations between the DRXed grain size,yield strength and extrusion parameters,the DRXed grain size and yield strength of as-extruded AXM100 alloy can be easily predicted at an optimal hotprocessing range.

4.Conclusions

In this work,the flow behavior,constitutive model,DRX kinetic model and processing map of a dilute RE-free solidsolution treated AXM100 alloy during the hot-compression under different deformation conditions were systematically investigated.In addition,the extrusion parameter optimization of the AXM100 alloy was performed based on the hotprocessing map.The main conclusions are summarized as follows:

1) After solid-solution treatment,a small amount of networkshaped Al2Ca phases are still retained in the matrix.The flow stress increases with the increase of strain rate or the decrease of deformation temperature during the hotcompression.The flow behavior is characterized by the typical DRX softening.

2) The activation energy of hot-compression is determined as about 205.7 kJ/mol.The conventional Arrhenius-type strain-related constitutive model is established.The conventional model works well for the flow curves at high temperatures (673 and 723 K) and low strain rates (0.001 and 0.01 s-1).However,large discrepancies exist between the predicted and the experimental results for the flow curves at low temperature and high strain rates.

3) Compared with the conventional Arrehenius-type model,the predictability is significantly improved by using the machine learning assisted model (SVR).The R value increases from～0.9806 to～0.9986,and the AARE and S.D.values shapely decrease from～11.5 to～1.23% and from～12.35 to～1.79,respectively.The SVR is an effective method to improve the accuracy of the constitutive models of Mg alloys.

4) The DRX kinetic model is established as follows:XDRX=for the solid-solution treated AXM100 alloy It is found that the nucleation of the DRXed grains having a typical necklace-shaped structure preferentially occurs at the original grain boundaries and the Al2Ca second phases.Subsequently,the CRSSs of non-basal slips reduce due to a relatively high deformation temperature,likely giving rise to the appearance of non-basal slips that also plays a pivotal role in the DRX process.The DRX process weakens the texture intensity.With further increasing the strain at a given deformation temperature,the DRXed grains also grow,accompanied by a weaker basal texture.

5) In the hot-processing maps,the increase of strain enlarged the instability domains.When the strain increases up to 0.6,the flow instability regions locate at two areas: 1) deformation temperatures of 573～683 K and strain rates of 0.03～1 s-1;2) deformation temperatures of 653～715 K and strain rates of 0.001～0.003 s-1.An optimal hot-processing range can be confirmed at the deformation temperatures of 600～723 K and the strain rates of 0.018～0.563 s-1.

6) According to the optimum hot-processing range,three kinds of deformation parameters are selected to perform extrusion tests.The results show that the as-extruded alloy at 603 K and 0.1 mm/s exhibits the best mechanical properties (i.e.,yield strength of～232.1 MPa,ultimate strength of～278.2 MPa and elongation-to-failure of～20.1%)than other two cases.A homogeneously fine-grained structure with a typical basal fiber texture and a certain number of nano-scale second phases (Al2Ca and Al8Mn5) provides an obvious grain boundary strengthening,texture strengthening and second phase strengthening.The maintenance of ductility is mainly attributed to a suitable grain refinement and microstructural homogeneity.

7) The relations between the DRXed grain size,yield strength and Z parameter can be expressed as follows:

When the deformation parameters are given,the DRXed grain size and yield strength can be predicted easily at an optimal hot-processing range.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This research was funded by the Postgraduate Research&Practice Innovation Program of Jiangsu Province (No.SJCX22_1720),the National Natural Science Foundation of China (No.51901204),the Chongqing Science and Technology Commission (Nos.cstc2020jcyj-msxmX0184 and cstc2019jscx-mbdxX0031) and the University Innovation Research Group of Chongqing (No.CXQT20023).

Supplementary materials

Supplementary material associated with this article can be found,in the online version,at doi:10.1016/j.jma.2022.07.013.