不对称独塔斜拉桥的结构参数敏感性分析

陈李俊

长沙理工大学 湖南 长沙 410004

独塔斜拉桥常建造较低高度的索塔，并使用预应力混凝土主梁，这导致了更高的刚度，一般有着三个无索长度。

与连续梁相比，部分斜拉桥的支点梁高约为梁高的0.6-0.4。斜拉桥近年得到了广泛的运用，越来越多的学者从各个因素响应进行研究，去评估桥梁结构在建造过程中的合理性及可靠性。

2006年，Chen,C.C ; Chou,H.Z[1]等人研究了不同刚度对桥梁的响应，发现了刚度到了临界值以后桥的荷载响应越来越小。

2013年，项海帆，肖汝诚，陈红[2-4]等在研究了双跨斜拉桥刚度，辅助墩数量，边中跨比各种单因素在不同环境下结构响应的影响，并建立了一套完整的斜拉桥结构体系。

2023年，李湘龙等人[5]，研究了斜拉桥施工过程中合拢桥梁线性和应力影响因素，并给出温度和一些外荷载是主要的影响因素，索力相对来说是次要影响因素。

以上所述，现有的研究集中在各种荷载和结构参数上的敏感性分析，很少或几乎没有考虑到两者之间的交互作用的影响和无索区长度这一因素，因此本文将以一座不对称独塔斜拉桥为背景去讨论这些随机变量，利用弯矩和变形来表征结构的可靠和安全性。并分析无索区长度、梁刚度、索刚度交互作用下敏感性分析，提出合理区间范围从而改进塔弯矩使其均匀并保证桥梁的安全性。

1 工程概况

建立的斜拉桥为两跨三部分，196+101+62m的跨度布置，主跨为196m图1为桥梁高程平面布置图，图2为主梁标准截面图。整体的静力研究使用了有限元的离散结构模型，主梁和桥塔是通过空间梁单元进行模拟的，斜拉索则是通过空间杆单元进行模拟的。主梁和塔是固定的，而且它们与辅助墩和边墩都是垂直约束和水平自由的约束形态。无索区长度为L=34m，主梁为宽度为29m的变截面预应力混凝土，图2为主梁标准截面图，主塔高127.586m，主塔截面为塔下柱为单箱单室，塔上柱部分为单箱三室的变截面预应力混凝土，主塔高度为127.586m。主跨和边跨分别有26对斜拉索，根据设计图纸，其中为了更符合真实的情况，张拉1486根预应力钢筋。

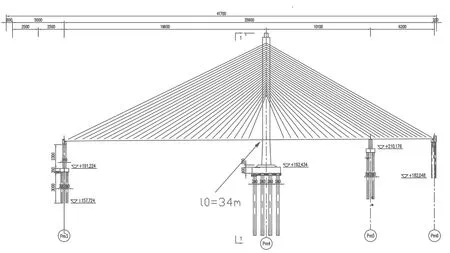
图1 桥梁平面布置图（单位：cm）

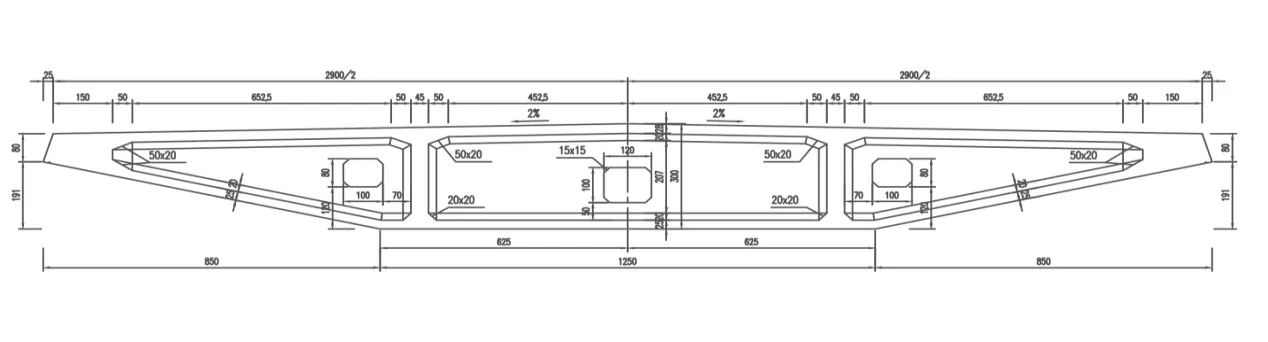
图2 主梁标准截面图（单位：cm）

图3 有限元模型

2 有限元分析模型的建立

本桥使用有限元软件（midas civil2020）模拟，斜拉索采用索单元模拟，主梁，主塔，桥墩，承台采用梁单元实现模拟，主塔与梁的连接采用刚性连接来模拟，边墩用一般支座来模拟。

混凝土容重为（25KN/m3），二期恒载考虑 10cm 厚铺装层与两侧护栏，合计按 100kN/m计入。

压重荷载为避免边跨辅助墩、边墩在最不利组合工况下出现负反力，在靠近过渡墩一定范围内施加压重荷载。其中离跨中80.225m-100m施加70KN/m均布力，102m-127.7m施加520KN/m均布力,128.3-320m处施加320KN/m均布力。

3 有限元单参数计算结果分析

利用主梁刚度EGIG、斜拉索刚度ECAC、塔根处无索区改变长度ΔL，分析了各载荷效应作用下主梁最大应力σB、主塔最大应力σT、塔顶挠度γT、主梁最大弯矩MB、塔根部梁的弯矩MBT、主塔最大弯矩MT的变化。主要参数的变化如表1所示。

表1 参数变化

3.1 斜拉桥主梁刚度结构刚度的影响

首先研究了主梁刚度的变化对整体结构力的影响。根据桥梁的有限元模型，改变主梁EG的弹性模量，主梁刚度为原刚度的0.1、0.5、1.0、2.0、3.0、4.0、5.0、6.0、8.0和10.0倍，其他参数保持不变。比较了主梁和索塔的内力和变形。计算结果如图4所示，其中M/∑M、γ/∑γ、σ/∑σ和分别表示当前EGIG'/EGIG条件下各临界部分的最大弯矩、变形和应力的比值，以及各计算组的最大弯矩和变形之和[5-6]。为了消除计算结果在数量级、单位、正负上的差异，采用归一化无量纲处理方法；表达式为

其中xij为第i组的第j个原始数据；yij是第i组的第j个原始数据的无量纲变换的结果；m是每组的数据数。

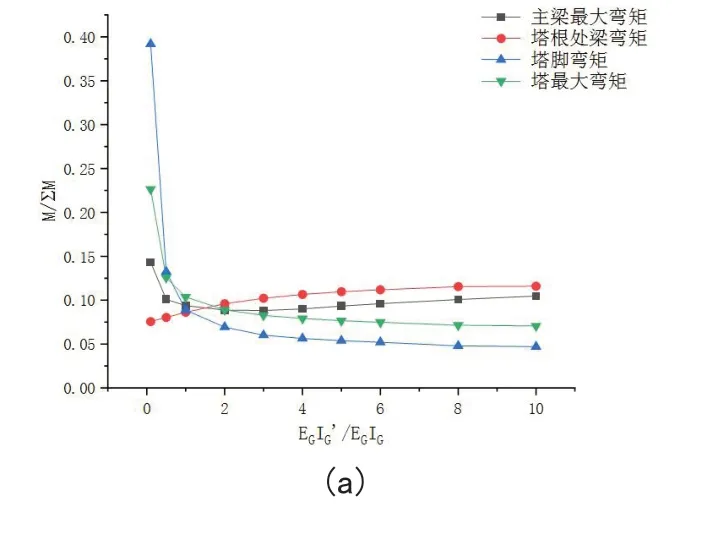
在图4中，随主梁的刚度的增大，当EGIG'/EGIG＜0.5时，主梁最大弯矩先呈现出下降的趋势，当EGIG'/EGIG＞1时，主梁最大弯矩缓慢上升，塔根处主梁弯矩随梁刚度的增加一直成上升的趋势，当EGIG'/EGIG＞4时，塔根处弯矩开始没有明显趋于稳定状态。当塔的最大弯矩出现在上塔柱和中塔柱交接处，塔的最大弯矩和塔脚处的弯矩随着梁刚度的变大，先呈现巨幅的下降，当EGIG'/EGIG＞1逐渐开始趋于稳定状态。时当 EGIG'/EGIG＜1时，主梁最大应力敏感性较高，梁最大应力最大值和最小值之间的差值为2%，当EGIG'/EGIG＞1,梁最大应力的增加趋势基本放缓。当EGIG'/EGIG＞4时，梁最大应力的变化趋于平稳。当 EGIG'/EGIG＜1时，塔顶挠度敏感性较高，塔挠度最大值和最小值之间的差值为33.5%，当EGIG'/EGIG＞2时，塔挠度在6.5%处趋于稳定的状态。当主梁刚度增大时，主梁承受的弯矩先剧烈减先后缓慢的增大随后趋于稳定的状态。然后塔根处的主梁弯矩则是一直增大的状态。由于主塔通过斜拉索承受的垂直荷载有限，因此主塔垂直荷载的变化较小，提高主梁的刚度将大大减少主塔的弯矩。

3.2 斜拉桥索刚度对结构的影响

一些斜拉桥的缆索在桥梁的整体受力中作用较小。然而，它们的轴向刚度对结构总体受力的影响不容忽视的影响。根据该桥的有限元模型，缆索刚度分别取为0.1、0.2、0.4、0.6、0.8、1.0、1.2、1.4、1.7和 2.0 倍，其他参数保持不变，计算结果如图5所示，其中M/∑M、γ/∑γ、σ/∑σ与上面含义相同。

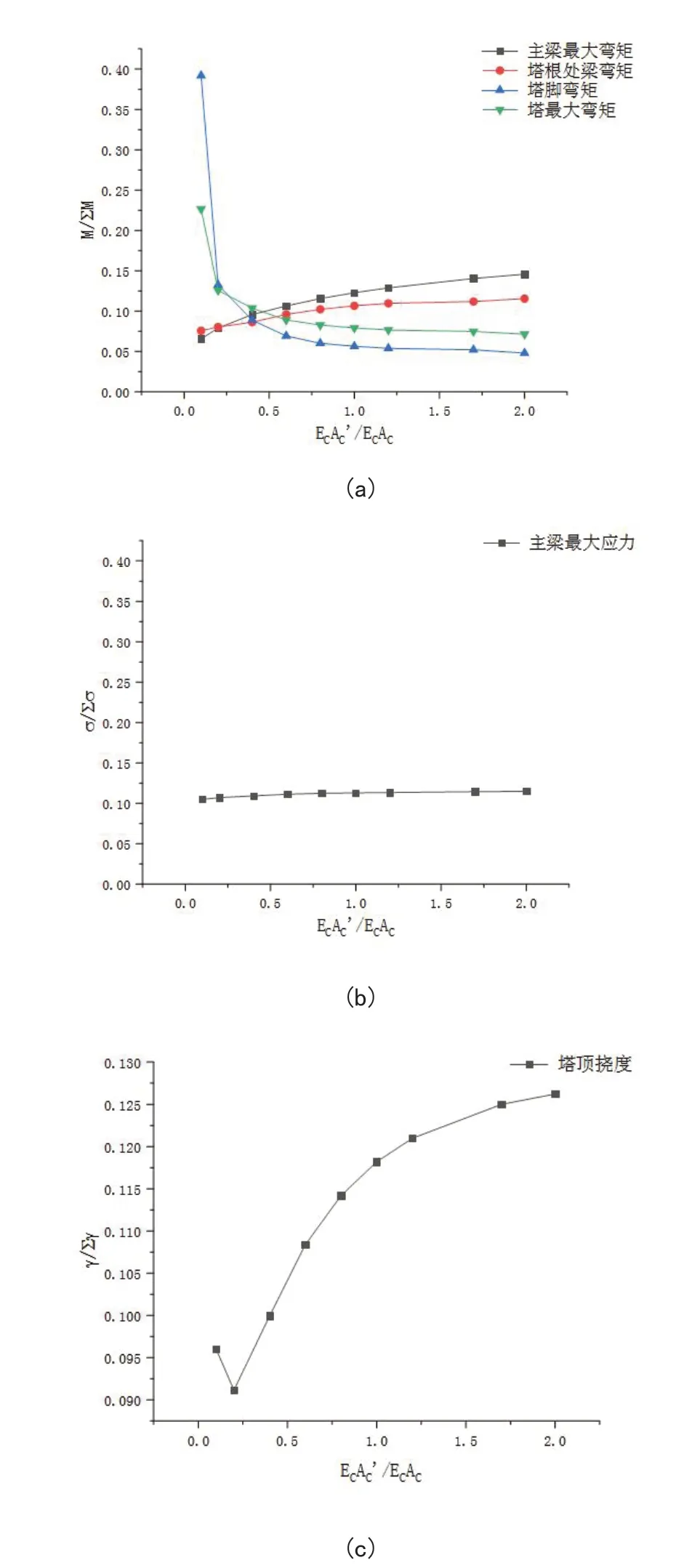
图5 索刚度对结构内力和变形的影响(a)弯矩;(b)应力;(c)挠度

在图5中，随索的刚度的增大，主梁最大弯矩和塔根处最大弯矩都呈现缓慢上升的趋势，ECAC'/ECAC＞1趋于稳定状态。主梁最大应力对索刚度敏感性基本为零。塔顶挠度随索刚度的上升，当ECAC'/ECAC＜0.25时，塔顶挠度呈下降趋势，ECAC'/ECAC＞0.2时，塔顶挠度呈上升趋势，在ECAC'/ECAC＞2.0时趋于稳定状态。由于缆索是柔性的，其内力并不遵循线性变化规律。随着刚度增大，缆索对力的传递效果增强，缆索将更多的垂直荷载传递给塔架，从而使梁的内力增加。将更多的垂直荷载传递给梁，从而导致缆索力的变化，进而引起结构力的变化。

3.3 斜拉桥塔根处无索区长度对结构的影响

计算结果如图6 所示，图中 M/∑M、γ/∑γ、σ/∑σ的含义与上表相同。与上图相同。改变无索区长度对主梁弯矩和对主梁弯矩和塔架弯矩的影响不同。探索改变塔根部的无索区长度对结构内力的影响，通过改变无索区长度变化值ΔL取为-1、2、4、8、12、14、16、20、24和28倍，其他参数保持不变，计算结果如图6所示。

图6 塔根处无索区长度内力和变形的影响。(a)弯矩;(b)应力;(c)挠度

图6 显示了主跨内力和主塔的内力和变形比较。随着ΔL/L 的增大，主梁弯矩和塔根部梁弯矩增大。随着而桥塔最大弯矩的弯矩则随着 ΔL/L 的增大而减小，塔脚处的弯矩则与塔身最大弯矩相反。塔脚的弯矩变化相反，主要是因为较长的斜拉索在无索区所承受的垂直荷载减小了。在无缆区内的斜拉索所承受的垂直荷载减小，而主梁所承受的垂直荷载增大，主梁承担了更多的垂直荷载。随着ΔL/L 的增大，塔顶的挠度和梁的应力基本保持稳定的状态。

3.4 总结

前面的计算结果总结并包含在下面的表2 中， 各关键部位的受力影响用强、中、弱来表示。

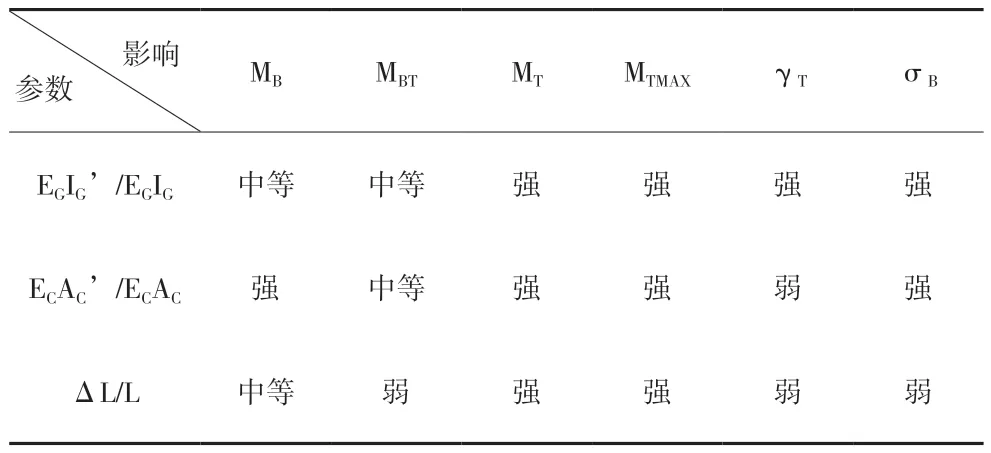
表2 参数总结

表3 优化参数的确定

4 优化方案数值模拟的确定和对比分析

建立表征最优参数组合的指标体系桥梁的整体静力性能。根据之前的计算结果包括刚度主梁、斜拉索刚度、无拉索区长度，并进行比较分析，图3得给出1.5＜EGIG'/EGIG＜3主梁最大弯矩不会明显增加，而塔的弯矩得到了明显的减小，且主梁应力的最大值和塔顶的挠度同时处于相比很小的状态。同理0.2＜ECAC'/ECAC＜0.4,索的刚度，然后塔根部无索区长度尽可能小一点取0.2＜ΔL/L＜0.3。

如下图7（a）可得出主最大正弯矩60000+远大于主梁负弯矩，达不到塔直梁平的理想状态，然后根据公式（2）

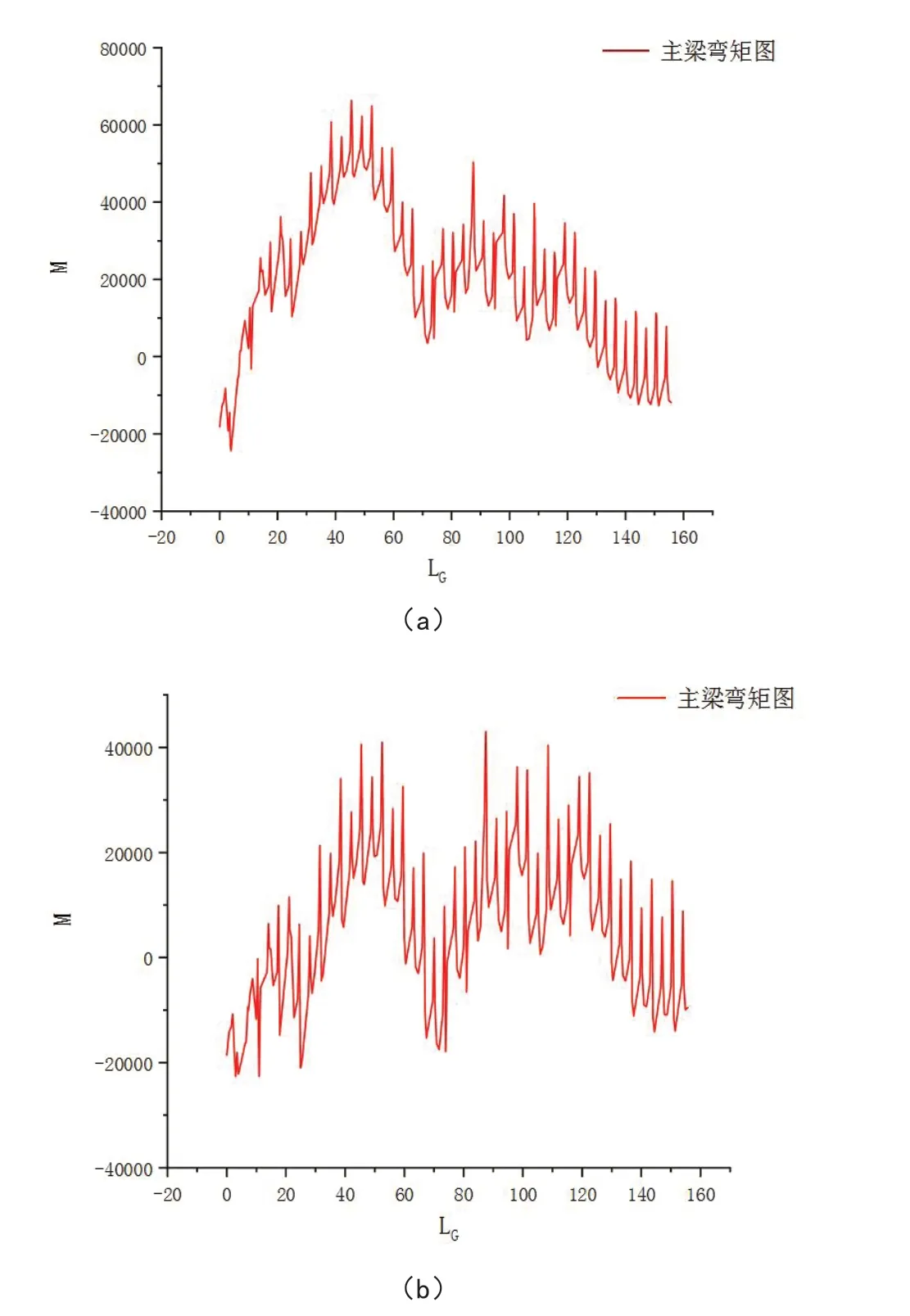
图7 原始模型和优化模型的主梁弯矩对比图（a）原始模型（b）主梁模型

式中[C]索力对弯矩的影响矩阵，施调向量{T},{M0}调索前弯矩[6]

式中[B]可以看做单元柔度对单元弯矩的加权矩阵[7]，也关于刚度的矩阵，证明了调节结构刚度能够给出合理的结构刚度的优化加权量，能得到相对理想的成桥弯矩，也从侧面反应了本文敏感性的意义所在。

然后本文优化的参数取值。

从图7中看出（b）图的主梁最大弯矩很明显的得到了下降从66331.4减小到了41153.2，达到了梁弯矩的相对理想的状态，正负最大弯矩相差不大。

5 结论

综上所述，通过比较分析，得出以下结论:

(1)当改变梁刚度EGIG时，0＜EGIG'/EGIG＜2内部结构力和变形敏感性较，当EGIG'/EGIG＞2当满足该条件时，刚性梁主梁刚度的变化对柔性独塔式斜拉桥对桥梁内力影响较小。

(2)索刚度对主梁弯矩和变形影响较大。随着刚度的增加，ECAC'/ECAC＜0.25主梁最大弯矩和塔根部梁弯矩增加趋势和塔顶挠度呈大幅度下降；主塔最大弯矩和塔脚处弯矩则与主梁最大弯矩相反呈现出更加敏感的下降趋势。ECAC'/ECAC＞1时，独塔斜拉桥的内力开始逐渐趋于稳定状态而塔顶挠度逐渐增加到ECAC'/ECAC＞2时趋于稳定。主梁的最大拉压应力一直处于平稳的状态。

(3)随着塔根部的无索区长度变化影响较大是塔脚处的弯矩和塔身最大弯矩而主梁的最大弯矩和塔根处的弯矩则是

(4)根据60个有限元模型和构件的独立参数比值的图例。主要的三个参数 梁刚度(EGIG)、斜拉索刚度 (ECAC) 和塔根处无索区长度变化值（ΔL）。根据此计算，最佳值范围为 参数如下： EGIG'/EGIG=1.5～3, ECAC'/ECAC=0.2～0.4且ΔL/L=0.2～0.3。三者呈耦合协调，并选取了EGIG'/EGIG=3、ECAC'/ECAC=0.2、ΔL=0.2，去比较了原始模型得出该取值范围能够对不对称独塔斜拉桥设计带来一定的帮助并且也可以给调整索力的给出方向。

不足之处没有建立三者的耦合模型，去对比耦合程度的高低，并没有考虑运营阶段的三者的灵敏度关系。