基于WOA-BP神经网络的板式定制家具车间电力预测模型

秦耀凯 陶 涛* 陈星艳 周昭龙 王雷东

（1.中南林业科技大学，湖南 长沙 410004；2.索菲亚家居股份有限公司，广东 广州 511358）

近年来，为推进生态文明建设和节能减排，我国提出了“双碳”（碳达峰、碳中和）战略目标，这对家具行业来说既是机遇又是挑战[1-2]。随着人民生活水平的不断提升，定制家具得到了越来越多消费者的青睐，源源不断的订单给工厂带来了大量的生产任务[3]。同时，工厂也产生了大量的电力消耗，不但增加了生产成本，还不利于企业落实“双碳”战略和节能减排。因此，车间电力节能和优化工作成为板式定制家具企业亟须解决的问题。板式定制家具生产属于传统制造业，主要能源消耗为电能。目前，绝大多数板式定制家具车间仍存在生产效率低下、能耗浪费严重等情况。此外，影响生产能耗的因素复杂多样，企业的关注度不高，相关研究较少，进一步导致了生产能耗的浪费[4-5]。

针对车间节能和能耗管理问题的研究主要有：车间节能优化调度、绿色和柔性生产、能耗预测、能耗分析和多目标优化[6-7]。其中，关于能耗预测的研究最多且最有效。用于车间电力预测的方法和模型有很多，传统预测模型有回归分析法、时间序列法、灰色预测法等；机器学习预测模型有小波分析法、支持向量机、人工神经网络等[8]。为了提高预测精度，一些学者会引入智能优化算法对神经网络进行优化[9-10]。尽管有关电力预测的研究较多，但大部分集中在建筑、能源、精密制造等领域，在定制家具行业的电力预测研究鲜有报道[11-12]。鉴于此，本文在深入探究电力预测模型原理及国外电力预测方法的基础上，使用一种基于WOABP神经网络预测模型对车间生产板件的电力能耗预测问题进行研究，以期解决车间生产的节能问题和能耗管理问题，从而推动板式定制家具企业积极落实国家的“双碳”战略。

1 板式定制家具生产过程电力能耗问题分析

1.1 问题描述

笔者对板式定制家具企业生产车间电力能耗的现状进行了调研和分析。调研发现，M企业几大生产基地每年电力能耗成本总和将近1.7 亿元，而每降低1%的能耗，则可节省170万元。目前，家具行业发展仍未完全摆脱粗放型生产模式[13]，车间自动化和信息化水平较低，因而无法对车间电力能耗进行数据采集、分析和管理。以上因素导致了板式定制家具企业生产制造车间的能耗使用效率低、电力能耗的成本居高不下等问题，给定制家具企业落实“双碳”战略、提质增效、节能减排和转型升级带来了挑战[14-15]。

1.2 板式定制家具生产加工过程和能耗现状

本文研究的板式定制家具企业的能耗主要为车间生产制造中所产生的能耗。板式定制家具的生产是车间加工制造设备通过消耗大量能量（主要为电能），将原材料转变为家具产品的零件或连接结构的过程[16-17]。在M企业中，车间生产主要有开料、封边、排钻和检验四大工序。本文研究的柜身自动车间，其主要使用设备为开料南兴380电子锯、封边610连线机和排钻拓雕双通道六面钻[18-19]。

1.3 加工设备电力能耗的影响因素分析

板式定制家具产品加工设备所产生的能耗主要分为固定能耗和非固定能耗[20-21]。固定能耗为待机状态下机器待机所产生的待机能耗和机器空载状态下所产生的空载能耗[22]；而非固定能耗为机器运转时各个加工单元所产生的可变能耗，主要由切削系统、进给系统、升降系统、温度系统等运行过程中所产生的能耗组成。影响开料工序能耗的主要因素有：1）原材料尺寸和厚度；2）原材料类型；3）锯切单元的锯切速度；4）推板单元的推板速度。随后，板件流转到封边工序。影响封边工序能耗的主要因素有：1）原材料尺寸、厚度和类型；2）进料速度；3）预铣刀速度；4）环境温度；5）开槽锣刀类型和速度。影响排钻工序能耗的主要因素有：1）原材料类型；2）打孔数量；3）打孔深度；4）钻头速度和类型。检验包装工序主要为人工操作，能源消耗较少，本文暂不考虑。

影响板式定制家具生产制造设备能耗的因素有很多，而其中有些影响因素，如原材料类型和刀具的种类等为非数字特征的数据结构，所以要对其进行预处理，将其转化为可识别的数字编码。经过梳理分析，板式定制家具生产车间的能耗影响因素和因素的取值范围如表1 所示。

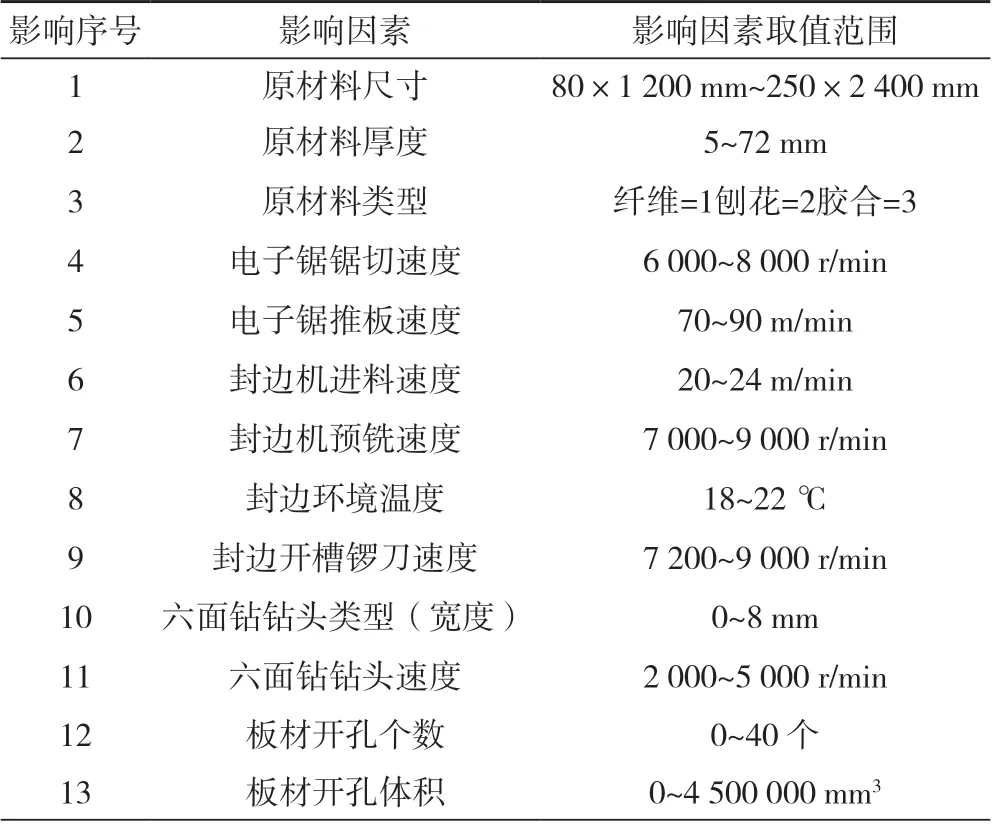
表1 板式定制家具生产加工过程能耗数据取值范围Tab.1 Range of energy consumption data values for the production and processing of customized panel furniture

1.4 问题求解思路

本文的研究对象为M企业的柜身车间。由于车间生产的加工设备在实际生产中会出现一些不可避免的数据丢失或异常等情况，为保证采集数据的真实性和可信性，采用日本横河生产的便携式电能质量分析仪对板件生产时加工设备的功率信号进行采集。通过实时采集，共采集到开料工序数据230组，封边工序数据454组，排钻工序数据207组。

针对上文提出的车间生产效率低下、电力能耗浪费严重、能耗影响因素复杂多样、企业关注度不高等一系列原因造成的电力能耗预测和管理困难的问题[23]，本文首先对板式定制家具的生产过程进行分析，梳理出影响车间生产能耗的主要因素。然后，采用电能质量仪对板件加工的实时数据进行采集，并对其进行预处理和分析。选用符合家具生产能耗特性的BP神经网络预测模型对板式定制家具车间生产能耗进行预测，并使用WOA算法对BP神经网络预测模型的阈值和最优权值等参数进行优化，并将其与传统的BP神经网络预测模型的结果进行对比，从而验证其有效性。板式定制家具车间生产的能耗问题具体研究求解步骤如图1所示。

图1 问题求解步骤Fig.1 Problem solving steps

2 WOA-BP电力能耗预测模型的建立

2.1 BP神经网络

BP神经网络（Back Propagation Neural Network，BPNN）是一种按误差反向传播训练的多层前馈网络，基本思想是梯度下降法，利用梯度搜索技术，以使网络的实际输出值和期望输出值的误差均方差为最小[24]。通过调整输入节点与隐层节点的联接强度和隐层节点与输出节点的联接强度以及阈值，使误差沿梯度方向下降。经过反复学习训练，确定与最小误差相对应的网络参数（权值和阈值），至此BP网络训练完成。

信号正向传播时，BP神经网络各隐含层的输入如公式 （1）：

式中：Ai为第i个隐含层的输入；m为输入层神经元数量；ωij为输入层神经元节点i到隐含层神经元节点j之间的权值；xi为输入层各向量；bt为隐含层神经元阈值。

各隐含层的输出如公式 （2）：

式中：Yi为第i个隐含层神经元的输出；f1为输入层至隐含层的传递函数。

输出层各节点的输入如公式 （3）：

式中：Sk为第k个输出层的输入；q为隐含层神经元数量；ωki为隐含层神经元节点k到输出层神经元节点i之间的权值；ak为输出层神经元阈值。

各隐含层的输出如公式 （4）：

式中：Qk为第k个输出层神经元的输出；f2为隐含层至输出层的传递函数。

单层输出与期望值之间的均方差如公式 （5）：

因此训练样本的误差如公式 （6）：

式中：E为均方差；b为输出层神经元节点数；Tk为第k个神经元输出期望值；N为训练集样本数量。

BP神经网络工作流程如图2所示。导入数据后，首先对BP的权重和阈值进行初始化。随后，确定神经元节点的数量和层次结构，并选择合适的传递函数来实现网络的非线性映射。对于输入数据的预处理，通常需要进行归一化或标准化操作，以避免特征值过大或过小而导致的精度问题。在训练过程中，需要设置合适的学习率、最大迭代次数等参数，并利用反向传播算法来进行误差反向传递和权重更新。最后，在预测阶段，进行反归一化操作以得到正确的输出结果。

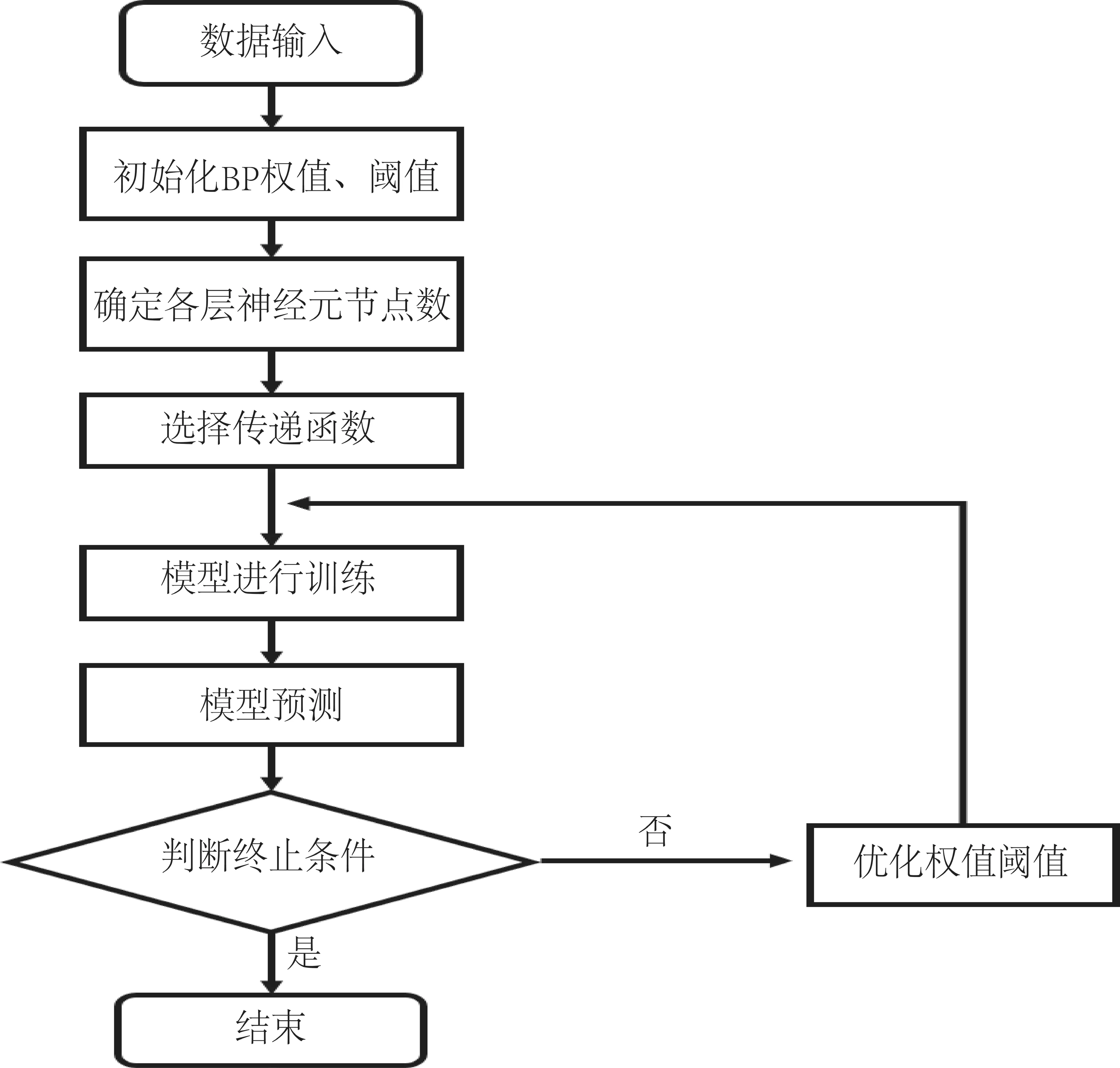
图2 BP神经网络工作流程Fig.2 BP neural network workflow

2.2 鲸鱼算法WOA对BP神经网络的优化和改进

BP神经网络功能十分强大，但也有局限性。例如，BP神经网络训练速度慢、测试稳定性较差、算法易陷入局部最优等[25]。为此，引入鲸鱼优化算法WOA（Whale Optimization Algorithm），建立WOA-BP神经网络模型。利用鲸鱼优化算法寻找确立BP神经网络的最优权值和阈值，并将该最优值应用于设定好参数的BP神经网络中，从而设计出最终的WOA-BP神经网络模型。

WOA算法的核心思想就是源于座头鲸特殊的泡泡网觅食法，通过随机或最佳搜索代理来模拟鲸鱼的围捕行为，通过螺旋来模拟泡泡网觅食的攻击机制，以此进行数学建模达到优化目的[26]。在WOA算法中，每只鲸鱼的位置可看做一个可行解，猎物的位置代表全局最优解，寻优过程为：

1） 包围猎物。首先确定好初始最优鲸鱼的位置，群体中的其它鲸鱼向其移动以包围猎物，则个体与猎物之间的距离D可表示为：

式中：d为当前迭代次数；X*为目前最优鲸鱼的位置向量；X为当前鲸鱼位置向量；A和C为表示系数；可计算为：

式中：r1和r2是(0,1)内的随机数；a的值从2～0 线性下降；dmax代表最大迭代次数。

2） 狩猎行为。鲸鱼通过螺旋游动的方式逼近猎物进行狩猎行为，数学模型可表示为：

式中：Dp为鲸鱼与礼物之间的距离；b为螺旋线形状；l为(-1,1)内的随机数。

鲸鱼通过螺旋游动的方式逼近猎物以缩小包围圈，在此过程中，假设由Pi的概率选择缩小包围机制和1～Pi的概率选择螺旋模型来更新鲸鱼位置，可表示为：

狩猎时，靠近猎物设定a减小，则A的波动范围下降。迭代过程中a从2到0下降过程中，A在(-a,a)内随机变化，当A在(-1,1)内时，鲸鱼的下一个位置是现在位置和猎物位置之间的任意点，因此设定A<1时，鲸鱼对猎物进行攻击。

3） 搜索猎物。搜索猎物时数学模型如下：

式中：Xrand为鲸鱼所处的随机位置，设定A≥1 时，随机选择鲸鱼的位置来更新其它鲸鱼的位置，迫使鲸鱼群体远离猎物以找到更合适的猎物，以加强算法的勘测能力对全局进行寻优。

WOA算法优化BP神经网络的流程图如图3所示，具体流程为：

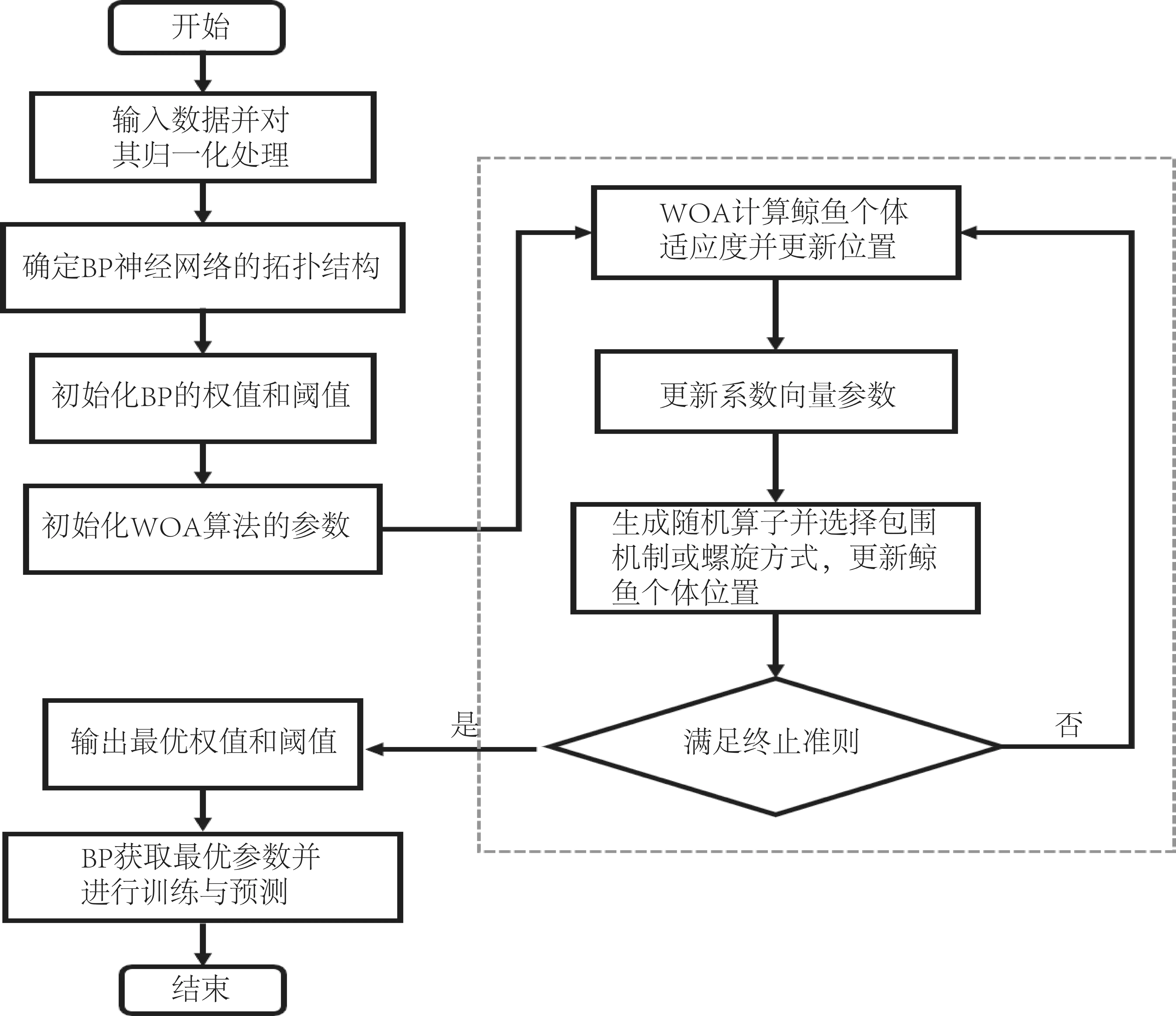
图3 WOA算法优化BP神经网络的流程Fig.3 Optimization of BP neural network process using WOA algorithm

1） 数据归一化，建立BP神经网络，确定拓扑结构并初始化网络的权值和阈值；

2） 初始化WOA参数，计算算法的决策长度，选取均方误差作为优化的目标函数；

3） 设置算法停止准则，利用WOA优化BP神经网络的权值阈值参数；

4） WOA算法优化后的最优权值阈值参数赋予BP神经网络，即输出最优的WOA-BP模型，利用WOA-BP进行训练和预测并与优化前的BP网络进行对比分析。

2.3 模型网络拓扑结构的确立

建立BP神经网路模型时，隐含层神经元数量的选择非常重要，数量较少时会导致网络学习程度降低，而数量较多则会导致训练过程较慢。隐含层节点数没有明确的要求，只能通过多次训练进行调整。隐含层神经元节点的设定有一个区间，可基于经验公式 （14）得出：

式中：m为输入层节点数；l为输出层节点数；a的取值范围为1～10。

开料工序能耗预测中，输入因素分别为板材厚度、板材尺寸、原材料类型、锯切单元锯片速度、推板单元进给速度5个因素，输出为能耗预测。通过经验公式可计算出本研究的隐含层神经元节点范围为3～12，带入到模型中进行训练寻优，计算不同隐含层节点的训练误差。在开料工序能耗预测中，当隐含层神经元节点数为10时，模型均方误差最小，为0.001 6。因此，开料工序能耗预测模型的网络拓扑结构为5-10-1。同理计算得出，封边工序能耗预测模型的网络拓扑结构为7-12-1，排钻工序能耗预测模型的网络拓扑结构为5-12-1。

2.4 WOA算法进化过程

WOA算法中的黑盒参数成为适应度函数，WOA算法的进化过程即为寻找函数最优解的过程。本研究中预测模型的适应度函数取为训练集和测试集整体的均方误差，WOA进化过程中，适应度越小，表明训练的模型越准确，模型的预测精度越高。本文参数设置为：训练次数为1 000，误差精度为0.01，学习率为0.01，显示频率为25，动量因子为0.01，最小性能梯度为1e-6，最高失败次数为6。初始化鲸鱼算法WOA参数：初始种群规模为30，最大进化代数为50。

初始化位置向量和领导者得分进行WOA进化。图4、图5、图6分别为开料、封边、排钻工序WOA算法的迭代进化曲线。由图可知，开料工序能耗预测模型的初始适应度值为0.70，进化第28代后曲线趋于平稳并保持不变，最佳适应度值为0.20。封边工序能耗预测模型的初始适应度值为0.24，进化第39代后曲线趋于平稳并保持不变，最佳适应度值为0.059。排钻工序能耗预测模型的初始适应度值为2.26，进化第35代后曲线趋于平稳并保持不变，最佳适应度值为0.17。

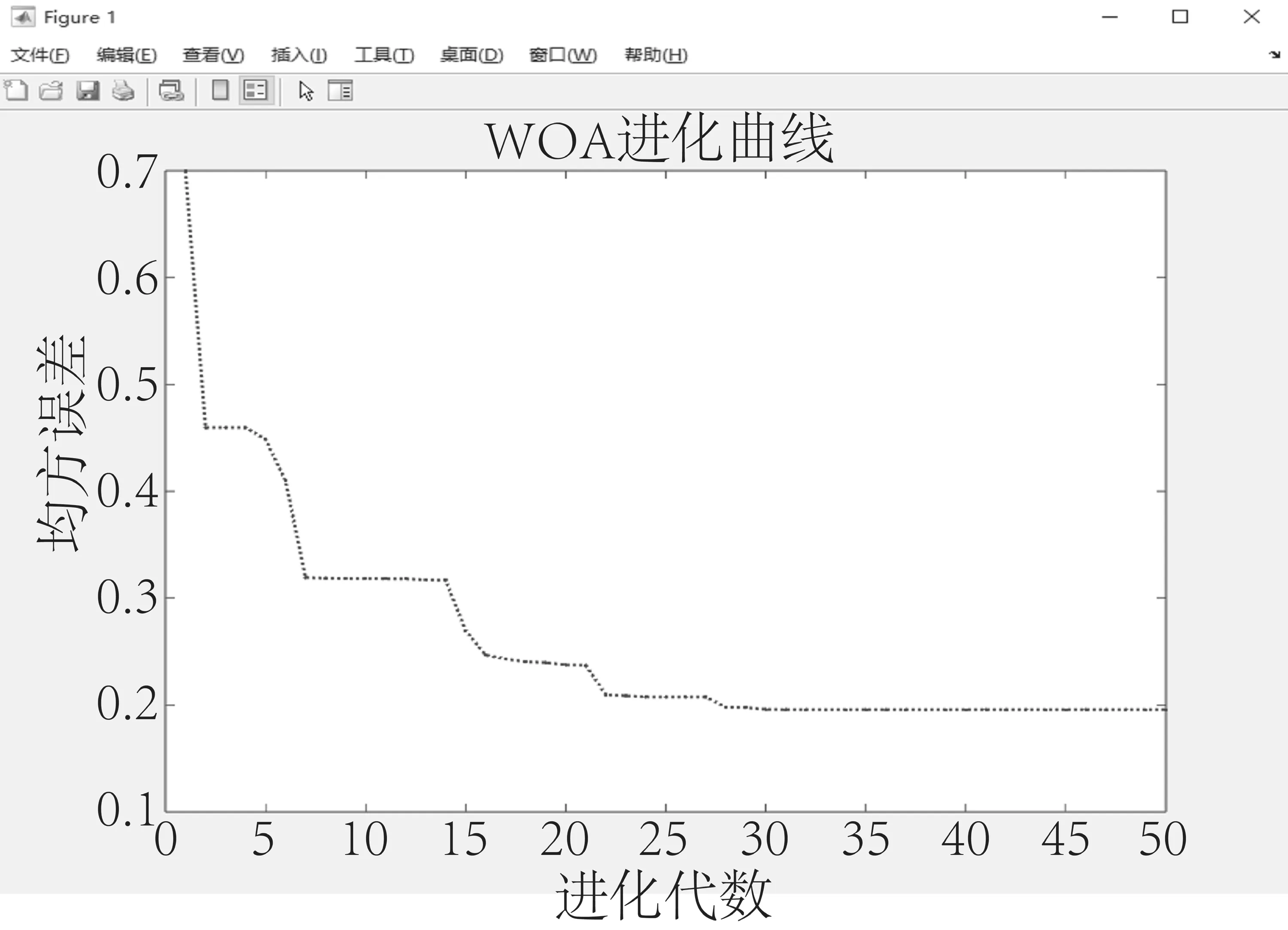
图4 开料工序预测模型适应度图Fig.4 Fitness of the cutting process prediction model

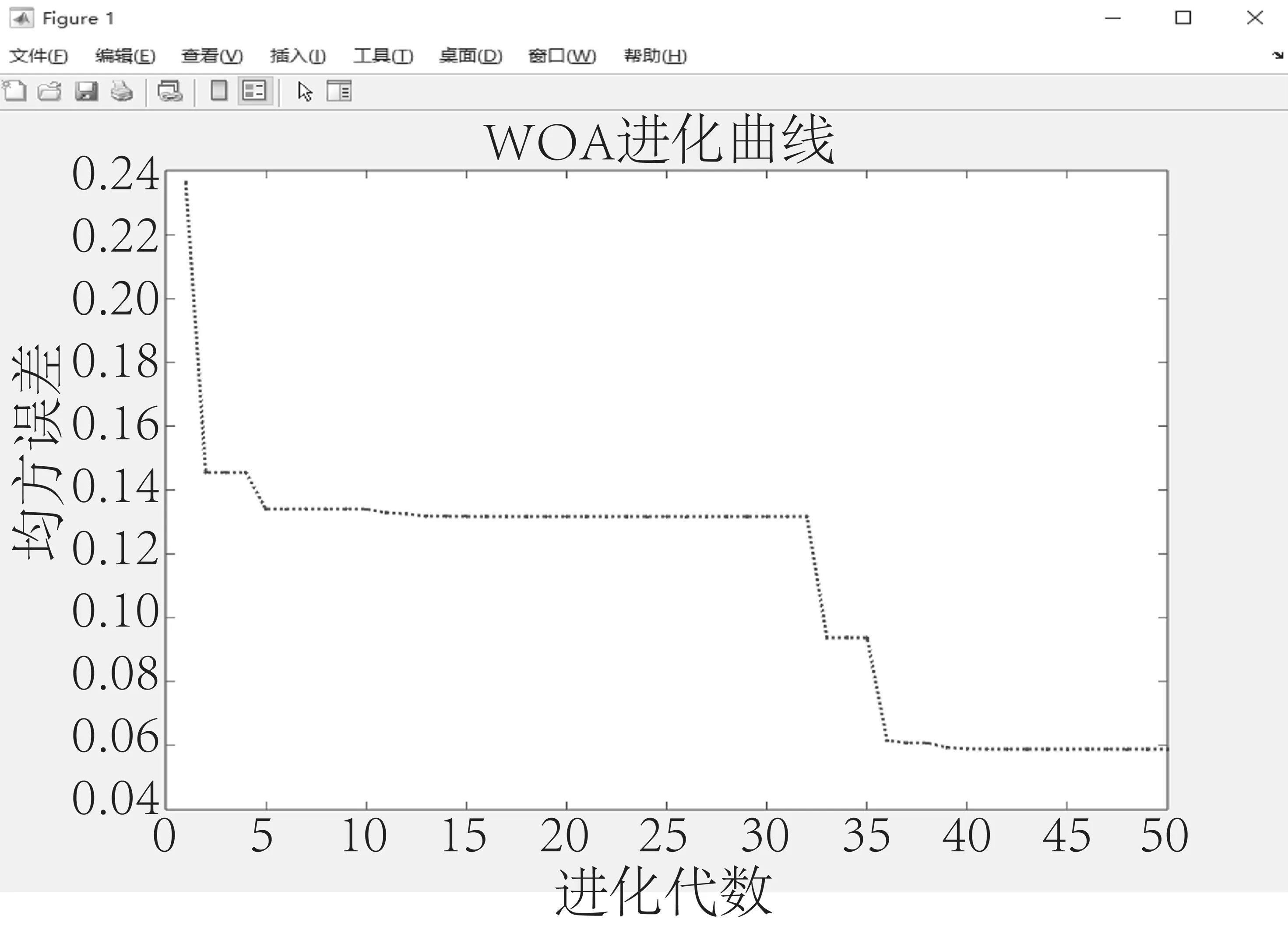
图5 封边工序预测模型适应度Fig.5 Fitness of the edge sealing process prediction model

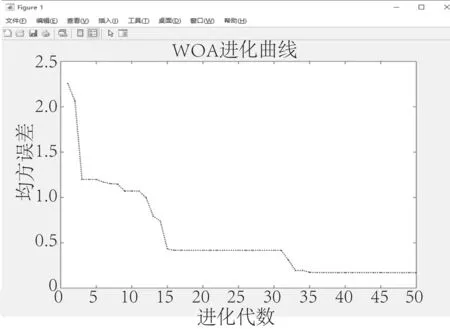
图6 排钻工序预测模型适应度Fig.6 Fitness of the drilling process prediction model

3 案例仿真结果分析

为验证WOA-BP预测模型的效果，将BP模型与WOA-BP模型在Matlab 2017平台上分别进行仿真试验。对板式定制家具生产车间设备进行能耗数据采集，开料工序能耗共有230组数据，其中随机选择180组作为WOA-BP预测模型的训练集，剩余50组作为测试集来评估模型对未知样本的预测精确度，即泛化能力。BP模型和WOA-BP模型对开料工序能耗的预测结果和预测误差如图7所示。从预测对比图中可以看出，WOABP模型的预测值更接近实际值，且误差曲线一直在0附近，误差非常小。经计算，BP模型的平均预测差值为1.70，预测准确率为95.28%，而WOA-BP模型的平均预测差值为0.23，预测准确率为99.44%。因此，WOA-BP模型的预测精度远优于BP模型。

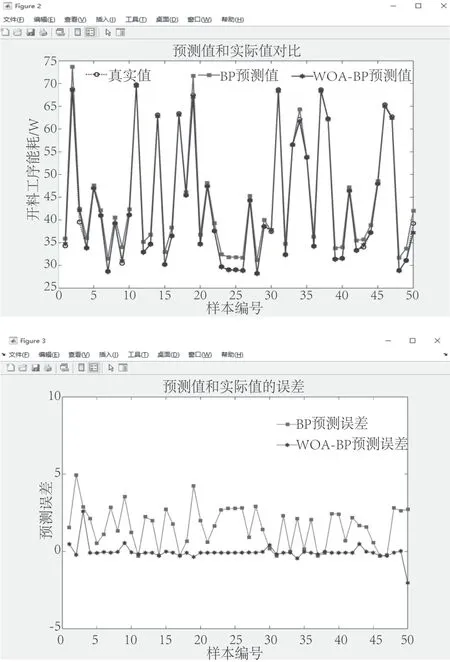
图7 开料工序能耗预测结果Fig.7 Prediction results of energy consumption in the material opening process

封边工序能耗共有454组数据，其中随机选择354组作为训练集，剩余100组作为测试集。测试集预测结果和预测误差如图8所示。从预测对比图中看出，WOABP模型的预测结果更接近真实值。经计算BP模型的平均预测差值为2.42，预测准确率为91.57%，而WOA-BP模型的平均预测差值为0.09，预测准确率为99.470%，表明WOA-BP模型的预测精度更优。

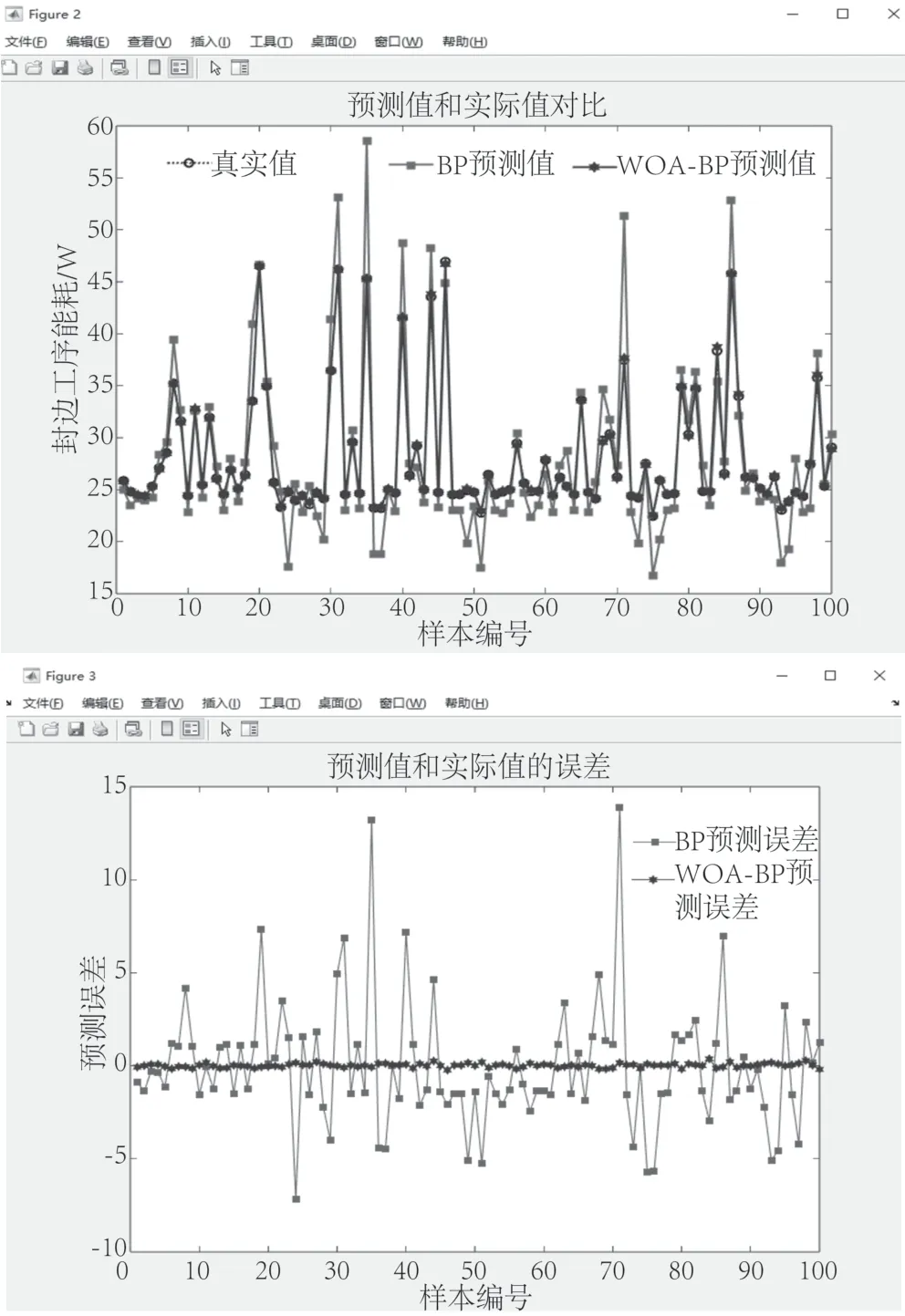
图8 封边工序能耗预测结果Fig.8 Prediction results of energy consumption in edge sealing process

排钻工序能耗共有207组数据，其中随机选择157组作为训练集，剩余50组作为测试集。测试集预测结果和预测误差如图9所示。从预测对比图中看出，BP模型的平均预测差值为5.85，预测准确率为90.73%，而WOA-BP模型的平均预测差值为0.32，预测准确率为99.44%，表明WOA-BP模型的预测精度更优。

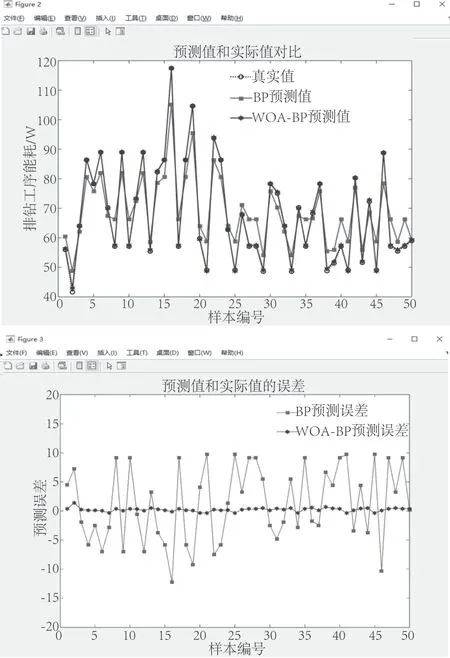
图9 排钻工序能耗预测结果Fig.9 Prediction results of energy consumption in the drilling process

如表2所示，WOA-BP预测模型的平均预测差值整体都远远小于BP预测模型，且WOA-BP预测模型平均预测差值在0.2以下。从表3中可以看出，WOA-BP预测模型的准确率整体都大于BP预测模型，其准确率在99%以上。可见，本文建立的WOA-BP能耗预测模型和选择的影响能耗因素都非常合适，也验证了WOA-BP能耗预测模型对于板式定制家具车间生产的电力能耗预测的有效性。

表2 BP预测模型和WOA-BP预测模型平均预测差值对比Tab.2 Comparison of average prediction difference between BP prediction model and WOA-BP prediction model

表3 BP预测模型和WOA-BP预测模型准确率对比Tab.3 Comparison of accuracy between BP prediction model and WOA-BP prediction model

4 结论

本文首先通过对板式定制家具企业生产设备能耗的主要影响因素进行分析，筛选出最优的影响因子。然后，选用BP神经网络预测模型对板式定制家具车间生产电力能耗进行预测，并使用WOA算法对BP神经网络预测模型的阈值和最优权值等参数进行优化，克服了传统的BP神经网络预测模型容易陷入局部最优解和稳定性差等缺陷。最后，通过对比仿真试验，进一步验证了WOA-BP神经网络预测模型的可靠性和准确性。因此，WOA-BP神经网络预测模型在板式定制家具企业生产制造车间的节能领域具有广阔的应用前景。

然而，本研究还存在一定的局限性。例如，没有使用更多的预测模型进行对比分析，预测模型的类型比较单一。因此，未来将对比更多的预测模型，使得算法的收敛速度更快，预测结果更加精准。