初中数学教学中数学思想的渗透

朱静军

⦿河北省唐山市第四十九中学

《义务教育数学课程标准》中明确提出把数学思想和方法作为基础知识的重要组成部分,可见其重要性非同一般.数学思想和方法是解决数学问题的重要工具[1],掌握数学思想和方法,既有助于教师的教学,又能够帮助学生形成良好的认识结构,促使其将书本知识转化为解决问题的能力,因此,在初中数学的教学过程中,教师要注重数学思想的渗透.

1 分类思想

分类思想主要体现在一些概念、定理、性质的应用中.在教学过程中,通过适当的说明和渗透,使学生对分类思想有一个较清晰的认识和掌握,更重要的是随着分类思想在学生头脑中的萌芽、生根、发展,使学生的思维能力逐步得到提高.

例1如图1,ABCDE是正五边形,问:以图中标明的字母为顶点、以已有线段为边的不同三角形有多少个?

图1

解法1：按三角形的顶点所在的位置来分类.

当三角形的三个顶点都在A,B,C,D,E中时,与△ABC全等的有5个,与△ACD全等的有5个,共10个;

当有两个顶点在A,B,C,D,E中,一个顶点在A′,B′,C′,D′,E′中时,与△A′CD全等的有5个,与△E′CD全等的有10个,与△D′CE全等的有5个,共20个;

当有一个顶点在A,B,C,D,E中,有两个顶点在A′,B′,C′,D′,E′中时均与△AC′D′全等,共5个.

所以,共有三角形10+20+5=35(个).

解法2：按三角形的边的位置分类.

当三角形有两边与正五边形的边重合时,均与△ABC全等,共5个;

当三角形只有一边与正五边形的边重合时,与△A′CD全等的有5个,与△E′CD全等的有10个,与△ACD全等的有5个,共20个;

当三角形没有边与正五边形的边重合时,与△AC′D′全等的有5个,与△A′BE全等的有5个,共10个.

所以,共有三角形5+20+10=35(个).

点评：这个图形并不复杂,但包含的三角形的个数却不少.如果硬数,常常会出现重复和遗漏.为了避免以上弊端,宜采取分类的方法,并且充分利用图形的对称性.从本题的解题过程中我们也能看到,同一个问题可以按不同的标准分类,当然,不能同时按照两种标准分类.

2 数形结合思想

数形结合思想贯穿于整个数学内容之中,运用数形结合法,借助“数”的精确性来阐明“形”的某种属性,能够把抽象的“数”的问题转化为直观的“形”的问题来解决;借助“形”的几何直观性来阐明“数”之间的某种关系,又能把复杂的“形”的问题转化为具体的“数”的问题来解决.

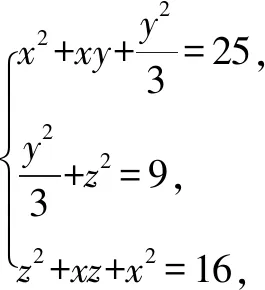
试求xy+2yz+3xz的值.

解析：将原方程组改写为

① ② ③

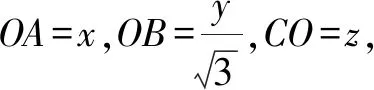
图2

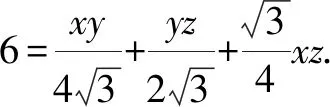
点评：本题已知条件是由三个二元二次方程组成的方程组,如果想尝试用解方程组再求值的方法来解题,在初中阶段显然很困难.因此可联想到利用勾股定理,通过对原方程组中的三个式子进行变形,构建以3,4,5为边长的直角三角形,即可化“数”为“形”,得到一种简捷解法.

3 方程思想

方程思想就是把研究的数学问题中已知量和未知量之间的数量关系,转化为方程等数学模型,让未知数参与运算,从而使问题得到解决的思维方法.方程思想贯穿于整个初中代数部分,通过方程的教学,使学生逐步形成方程意识,不仅能够简化和加速思维的进程,还能够解决一些较复杂的数学问题和实际问题.

例3如图3,已知AC切⊙O于点C,CP为⊙O的直径,AB切⊙O于点D与CP的延长线交于点B,若AC=PC.

图3

求证:(1)BD=2BP;

(2)PC=3BP.

证明：(1)如图4,连接DO,设PO=OC=DO=x.

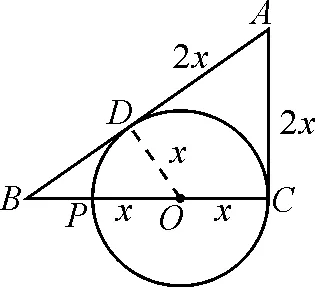
图4

∵AC,AB切⊙O于点C,D,AC=PC,

∴AC=PC=AD=2x,∠ACO=∠ADO=90°.

∴△BOD∽△BAC.

∴BO∶AB=OD∶AC.

即(BP+x)∶(2x+BD)=x∶2x,化简得BD=2BP.

(2)在Rt△BOD中,由勾股定理,得

OB2=OD2+BD2.

即(BP+x)2=x2+(2BP)2,化简得2x=3BP.

点评：本题的证明中充分利用了方程思想,通过寻找相等关系,以运算代替论证.例如,题中的PO=OC=DO=x,AC=PC=AD=2x,BP,BD这些未知数都参与了运算.

4 转化思想

数学问题的解决过程就是一系列的转化过程,转化是化繁为简、化难为易、化未知为已知、化陌生为熟悉的有力手段,是解决问题的一种最基本的思想.前苏联著名数学家C·A娅诺夫斯卡娅曾一语道破解题的本质:“解题,就是意味着把所要解的问题转化为已经解过的问题.”问题转化得好,就能得心应手,游刃有余.而具体转化的方法也有很多,例如添加辅助线、构造方程或不等式、图形的分割拼合、画图象、代数式的变形等.

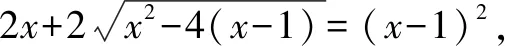
2x+2|x-2|=(x-1)2.

④

若x-2≥0,则④式可化为4x-4=(x-1)2,解得x=5,或x=1(与x≥2矛盾,舍去).

若x-2<0,则④式可化为(x-1)2=4,解得x=3,或x=-1.由于x=3与x-2<0矛盾,x=-1与x-1>0矛盾,故都舍去.

综上所述,方程的解为x=5.

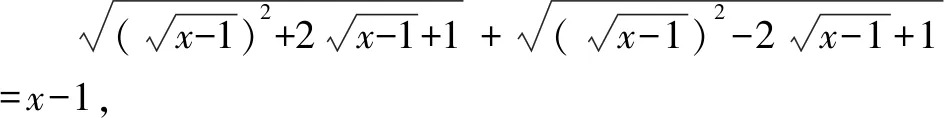
《暂行办法》规定，在一个纳税年度内，与基本医保相关的医药费用，扣除医保报销后个人负担累计超过15000元的部分，由纳税人在办理年度汇算清缴时，在80000元限额内据实扣除。此前的征求意见稿中，限额为60000元。

化简得

⑤

综上所述,方程的解为x=5.

点评：本题的两种解法,都是通过以下转化途径,即由二重根式的无理方程—一重根式的无理方程—绝对值方程—整式方程,将复杂的问题转化为简单的问题,将不熟悉的问题转化为熟悉的问题.

5 整体思想

初中数学教材中应用整体思想的知识也很多,在解决某一问题时,不能独立、孤立地看待,而是要通过观察,把着眼点和注意力放在问题的整体结构上,才能触及到问题的本质,从而达到求解的目的,这就是整体思想.整体思想是解决数学问题的一个重要策略,也是提高解题速度的有效途径[2].

5.1 整体代换,化难为易

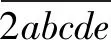
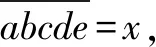
故所求六位数是285 713.

点评：本题中的a,b,c,d,e是五个未知数,按照通常的思路需要列五个方程才能获解,但是这样做很困难,关键是根本就找不到五个方程.如果换个思路看,观察出这五个字母结合的顺序没有变动,不妨把这五个字母看成是一个数,也就是把它当作一个整体,这样就化难为易了.

5.2 整体代入,化繁为简

例6已知x2+3x+5=7,求3x2+9x-2的值.

解析：3x2+9x-2=3(x2+3x+5)-17
=3×7-17
=40.

点评：本题如果按照我们平时的解题习惯,通常是先解方程x2+3x+5=7,得出x的值,再代入代数式3x2+9x-2中求值,这样显然很繁琐.稍加观察我们发现,两个代数式中的二次项和一次项的系数成比例,因此可以考虑用整体代入法.当然,本题还可将x2+3x作为整体(=2)代入求解.

5.3 整体思考,打破常规

例7试证明:两个一元二次方程x2+ax+a=0,x2-x-2a-1=0中至少有一个方程有实数根.

证明：由题意得,Δ1=a2-4a,Δ2=1-4(-2a-1),则Δ1+Δ2=(a2-4a)+[1-4(-2a-1)]
=a2+4a+5
=(a+2)2+1.

因为(a+2)2≥0,所以(a+2)2+1>0.

故Δ1,Δ2中至少有一个大于0,即两个方程中至少有一个方程有实数根.

点评：本题如果按照常规思路,逐一考虑两个方程,由于a值的不确定性很难证明.但如果换个思路,将两个方程的判别式的和作为一个整体考虑就容易多了.

除了上述数学思想,还有其他如类比、归纳、辩证、函数、构造、换元等数学思想可以运用.在数学教学中,应结合实际,重视这些数学思想的渗透,这样有助于发展学生的思维,培养数学能力,提高综合素质.