幽默引人入胜 留白发人深省 结语绕梁三日
——初中数学课堂教学语言艺术提升研究
陈秀海
⦿ 江苏丰县华山镇华山初级中学
作为一名初中数学教师,如何在课堂教学语言上体现特色,发挥语言的魅力,让数学教学更加深入浅出、通俗易懂,直接影响着数学课堂的质量.本文中就数学教学语言艺术提升问题着手进行研究分析[1].
1 幽默的讲解吸引学生注意力
1.1 言之有趣,妙趣横生
课堂的导入,特别是新课的导入,妙趣横生的导语能吸引学生的注意力,让其主动投入到数学学习之中.在讲授“解任意三角形”时,笔者先问:“同学们,你们不过河能测出河面的宽度吗?不上树能量出树高吗?不走近敌方阵地能测得敌我双方阵地之间的距离吗?”接着指出:我们通过这节课学习“解三角形”就可以解决这些问题了.这样的导入,能引起学生对所学内容的浓厚兴趣.
1.2 言之有情,情理交融
知识本身是无情的,但是我们的教学是有情的.教师的任务就是将无穷的知识转化到有情的教学过程中,让知识变得有“文气”“人气”,让学生能感受到知识的温度,从而在接受知识的过程中不再冷淡.因此,课堂教学需要“有情”“有温度”的语言.也许只有这样,才能让学生真正融入到教学中,感受到课堂的真正意义.
1.3 言之有启,因势利导
苏霍姆林斯基曾说过:“教学的技巧并不在于能预见到课堂的所有细节,在于能根据当时的具体判断,巧妙的在不知不觉中作出相应的变动.”课堂是多变的,其中一定存在着不可预设的意外,需要教师针对性的启发引导,需要有一双慧眼,透视课堂,敏锐捕捉.
1.4 言之有度,展示艺术
数学课堂教学语言艺术的风趣体现在教师独具匠心的创造力上.严密的符号体系、独特的公式结构、形象的图象语言,如果用学生喜欢的、生动有趣的而又不失数学知识精髓的语言表达出来,那么数学课堂就不会再让学生感到枯燥无味、繁琐杂重.在教学过程中笔者也在想一些点子让学生接受更简单的数学知识,如编成谚语、古诗等样式来引导学生掌握.例如,在学生解分式方程时,笔者编写了“锄禾日当午,同乘公分母,解个小方程,验根解写出”.
2 简单的留白发人深省、促进思考
2.1 提问过程中的留白艺术
(1)教学语言严谨中不失留白
严谨,顾名思义,严肃谨慎,不但要求准确,更要体现规范.例如,在讲述圆心角和圆周角的关系时,将圆周角顶点A的位置故意留白,引导学生体会弧BC所对的圆周角的位置关系,从而引导学生在理解点A的位置上体会严谨性.
(2)注重教学语言的灵活性
要用形象化的语言去解释抽象的数学概念、数学公式.一般来说,对人的感官富有刺激性的语言,最能引起学生的兴趣.在学习探寻数据规律时,笔者给学生展示了1+2+3+……+2 020,让学生来计算,很多学生却摇头无语.其实,这个问题学生在小学三四年级就可以很简单地计算出来了,现在怎么不会呢?笔者将梯形公式展示出来,结果同学们一验证,还真是,从算法到意义,巧妙地将一些常见的公式用在复杂问题中,让学生记忆深刻,终生不忘.
(3)注重教学语言的启发性
要精心锤炼描述性的语言,把学生带入美的意境,数学教学中偶尔出现几句诗情画意的语言,效果更是不同凡响.据说陈景润的老师曾经用诗一般的语言向学生介绍了哥德巴赫猜想:自然科学的皇后是数学,数学的皇冠是数论,而哥德巴赫猜想则是皇冠上的明珠.他还意味深长地说:“昨天晚上,我做了一个梦,梦见你们中的一位同学了不得,他证明了哥德巴赫猜想.”这句话产生的神奇的力量,激励陈景润开始摘取皇冠明珠的万里长征,他矢志不渝,百折不回,终于创造了数学的辉煌.
(4)注重教学语言的规范性
对于数学语言,要求得非常规范.常常出现的“除”与“除以”、“切线”与“切线长”等如果混为一谈,就违背了同一律;又如有的教师讲“圆中相等的圆心角所对的弧相等”“圆锥的体积等于圆柱体积的三分之一”,就忽略了“同圆或等圆”“同底等高”的条件;再如对“90°”和“垂直”两个概念的理解,都必须用规范的语言进行说明.
2.2 讲述过程的留白艺术
(1)情感方面的留白
情感留白,有时候在课堂上可以让学生对问题更加关注,思考更认真,体验更深刻,从而实现对数学文本的更深层次的理解与把握.例如,在讲述销售问题时,面对“要获得利润5 000元”,我们该怎么安排物品的售价呢?按照常规根本不能实现这一要求呀?怎么办?在关键环节故意流露出难以解决的表情,激发学生的情感,与之共鸣,进一步调动学生的思考力.
(2)内容方面的留白
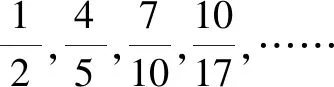
(3)问题研究的留白
问题留白,可以历练学生的思维品质.针对一些问题,也可根据问题情境设计不同的留白,特别是在旋转问题、动点问题的研究过程中,注意适时留白,让学生自己来思考研究,这样会给学生更多的表现机会.诸如像常见的“45°模型”“一线三直角模型”等,面对出现的疑问该怎么处理呢?将问题留白,引导学生小组内研究分析,找到方法并进行归纳,形成模型,让学生能够举一反三.
3 巧妙的结语引导学生学思结合、拓展延伸
数学知识的前后联系密切,特别是一些螺旋上升的知识串,更是交叠在一起的,讲述过程需要逐步深入,循序渐进,让学生在把握过程中进行类比,得到感悟与启迪,如果语言再具有诗情画意的感染与启发性,那效果就会更好.
例如,在讲述整式的加减运算过程中结合图形探究整式规律性问题时,从简单的问题提起,学生很容易把握,但是随着数字的变化,学生的思维似乎变得迟钝,于是就将要求变成“求救”:如果我要得到第100个图形,怎么计算其中的个数呢?面对疑难求助,学生深入思考的力度就大了.再追问:第2 023个图形呢?我们将这些具体的数字用字母替换一下会怎么样呢?学生在分析过程中就会得到启示,用字母表示数的思维变换就得到了推进,问题就会迎刃而解.
如果语言能将学生带入诗情画意之中,那么学生会更铭记深刻.据说我国数学家陈景润曾用诗意的语言介绍哥德巴赫猜想,进一步激发学生的数学求知欲.
课堂的结语,往往是课堂知识精髓的最后呈现,体现的内容是重点、难点、关键点甚至是画龙点睛的内容.巧妙的结语不仅让学生对知识的记忆更加深刻,更能让学生对所学知识进一步升华,似乎感觉余音绕梁,再有奋力探究的劲头.
3.1 画龙点睛式的结语
一堂课的结束,不能简单地用几句话做个总结就可以了,还需要深化课题内容,让学生进一步得到余味,更要从这节课的主题思想中感受到数学的博大精深,将学生带入到另一个层面的未知王国之中.在学习勾股定理后,展示了数学家毕达哥拉斯根据勾股定理所画的“勾股树”.当一个巨大的“勾股树”展现在学生面前时,直观的画面让学生眼前一亮.这种画龙点睛之笔的结语虽然没有铿锵的语言,但也让学生产生震惊的同时,记忆深刻,感悟颇深[2].
3.2 承上启下式的结语
(1)知识上的承上启下.问题是数学的心脏,可见提问方式的不同,取得的效果也不同.大多数的新知识都是在旧知识的基础上延伸和发展的,在新旧知识的衔接处要注重提问的技巧,尤其在一些暗示性的问题上要寻求突破,将知识点上下贯通,从而使得学习有序巩固落实.
(2)方法上的承上启下.整个教学过程中,将课堂还给学生,放手让学生自主学习,让他们真正成为学习的主人.通过问题,引导学习从已有经验出发,尽情表达对于知识的理解,真正感受到自己是学习的主人,哪怕有的学生只说一句,或者知道意思但表述不清楚的,都要给予充分的肯定和鼓励.
(3)思维上的承上启下.当学生对问题的把握不是很准确时,往往停留在原来的思维定势之上.若采用承上启下的引导,思维有了变通,新旧知识有了联系,解决问题的设想就变得丰富多彩.如遇到求解两条线段求和的最小值问题,往往想到“将军饮马”,看到类似“PA+kPB”形式求最值,通过思维定势,会思考“胡不归问题”与“阿氏圆”等等.当思维能够承上启下时,问题就会在解答过程中变得通透.
总而言之,课堂教学是教育者的人生舞台,教学是一门永无止境的艺术,想在课堂之上真正实现知识的传授,学生能力的培养,就要不断提升课堂语言表达的艺术魅力.只有这样,课堂才会焕发出生命活力,“柳暗花明”,这样的课堂才能变得枝繁叶茂.

