基于CCA和多通道循环维纳滤波的滚动轴承故障源分析

张伟涛, 张东江, 纪晓凡, 黄 菊

(1．西安电子科技大学 电子工程学院,西安 710071; 2．中国航发贵阳发动机设计研究所,贵阳 550081)

航空发动机主轴轴承长期工作在高温、高速、重载的严苛工况下,由于疲劳剥落或异物进入等原因,很容易同时在轴承滚道和滚子上产生缺陷,缺陷多为复合缺陷,微弱的故障会在较短时间内发展为严重故障,因此对轴承故障的及时诊断成为近年来的研究热点。针对航发主轴轴承的故障诊断问题,可以通过分析温度、振动、声发射等不同传感器的数据来实现,其中利用振动信号实现的故障诊断方法得到了广泛应用。

由于航发主轴轴承运转环境的复杂性,用于轴承状态监测的振动传感器一般只能布置在轴承座或设备机壳上,因此传感器阵列采集的多通道信号一般是包含多个信号源的混合振动信号,其中包含轴承结构本身引起的振动,也包含除轴承以外的其他发动机附件引起的振动,当轴承的某些部件存在故障时,采集信号中也包含了由于轴承缺陷引起的振动。例如异物进入滚道很可能同时造成内圈和外圈划伤,因此采集的信号将包含多个故障源的振动信号。在滚动轴承复合故障诊断中,为了更好地分析轴承故障特征,完成故障定位,有必要从采集的信号中恢复单一故障源信号。

近年来针对轴承复合故障诊断在各不同行业的应用,文献中提出了一些可行的方法[1-4],主要分为传统信号处理方法和基于机器学习的处理方法。传统信号处理方法[5-8]是将各种信号分解方法(包括:短时傅里叶变换、小波变换、经验模态分解、局部均值分解、固有时间尺度分解、变分模态分解等)与包络谱分析相结合,进行信号降噪和干扰抑制,然后提取故障特征频率,与轴承组件的理论故障特征频率进行比对实现轴承缺陷识别。这类方法计算高效,适用于轴承状态在线监测,工程应用性强,一直是研究的热点,但这类方法的故障诊断效果对信噪比和干扰强度比较敏感,故障诊断的可靠性有待提高。基于机器学习的处理方法[9-14]从时域、频域或时频域进行信号降噪和故障特征提取,或通过信号处理方法降噪后与非线性动力学方法相结合完成故障特征提取,然后利用提取的特征训练一个故障判别模型,例如:支持向量机、循环神经网络、卷积神经网络、自编码器等,最终使用训练好的模型进行故障分类。这类方法属于数据驱动型故障诊断方法,前期需要大量的样本数据对模型进行训练,其性能依赖于可获得的样本数量以及质量,比较适合单一故障和恒定工况下的故障诊断,但不适合复合故障和复杂多变工况下的诊断。

由于航发主轴轴承的工况复杂多变,获得宽转速范围和载荷下主轴轴承多个不同故障模式的大量振动数据变得异常困难,因此本文聚焦于复合故障分析的传统信号处理方法。循环维纳滤波算法[15-20]是一种典型的信号处理方法,它主要利用轴承故障信号的循环平稳特性恢复观测信号中的故障源信号,根据期望信号选取方式的不同,可以分为两种:第一种是以观测信号本身作为期望信号的直接循环维纳滤波方法,这种方法能够消除观测信号中的环境噪声,但只适用于轴承单一故障诊断,不适合轴承复合故障诊断;第二种是以人工合成信号作为期望信号的循环维纳滤波方法,其提取效果十分依赖轴承的先验信息。为解决循环维纳滤波方法中期望信号无法有效获取的问题,本文提出了基于规范相关分析(canonical correlation analysis, CCA)盲信号提取的期望信号生成方法,推导了基于共轭梯度的优化算法,以CCA盲提取得到的故障特征信号作为期望信号,克服了现有循环维纳滤波算法的不足。此外,在轴承振动信号采集过程中,由于传感器安装位置不同,不同通道的观测信号信噪比差异较大,因此单通道循环维纳滤波方法的故障诊断效果对通道选择非常敏感。针对这个问题,本文提出了基于多通道循环维纳滤波的滚动轴承复合故障诊断方法,该方法利用所有通道采集的振动数据,自适应地调整不同通道权重,进一步提高了故障诊断的可靠性。

1 轴承振动信号数学模型

本文主要考虑航发轴承试验机上的振动信号采集与分析。轴承振动信号采集示意图如图1所示。源信号包括轴承故障源信号和其他振动干扰信号,根据故障点所在组件的不同,常见的轴承故障源主要包括外圈故障源s1(t)、内圈故障源s2(t)以及滚动体故障源s3(t),振动干扰信号来自于机匣上的各种附件设备,主要是油泵振动干扰s4(t)。用于轴承状态监测的传感器一般只能布置在轴承座或机壳上,例如图1中轴承座上布置了加速度传感器AC1,外壳上布置了加速度传感器AC2和AC3,t时刻传感器AC1采集得到的振动信号x1(t)可表示为

图1 轴承振动信号采集示意图Fig.1 Schematic diagram of bearing vibration signal acquisition

(1)

式中:a1q为第q个源信号到传感器AC1的路径衰减系数;n1(t)为AC1的传感器噪声。假设在不同位置共布置M个传感器,采集N个不同振动源的振动信号,则第m个传感器接收的观测信号xm(t)可表示为

(2)

式中:sn(t)为第n个振动源信号;amn为第n个源信号到第m个传感器的路径衰减系数,它一般是未知的。令x(t)=[x1(t),…,xM(t)]T为同时采集M个通道获得的信号向量,那么x(t)可为

x(t)=As(t)+n(t)

(3)

式中:s(t)=[s1(t),…,sN(t)]T为N维振动源信号向量;A为M×N维混合矩阵,表示N个源信号到M个传感器的未知路径衰减系数;n(t)=[n1(t),…,nM(t)]T为M维传感器噪声向量。

滚动轴承的故障形式包括点蚀、磨损、裂纹等,轴承在旋转过程中会产生脉冲信号,在不同元器件上的故障会产生不同的脉冲信号,对应频率称为故障特征频率,其中内外圈故障较为常见,其对应的故障特征频率计算公式分别为

(4)

(5)

式中:fi为内圈故障特征频率;fo为外圈故障特征频率;v为轴承转速;a为接触角;Dm为节圆直径;z为钢球数量;d为钢球直径。轴承滚动过程中产生周期性脉冲信号,其二阶统计量呈现周期平稳性,因此轴承振动信号属于循环平稳信号。也已证明[21],故障轴承的振动信号会以调幅波的形式出现,其循环频率对应故障特征频率及其倍频,因此本文使用故障特征频率及其倍频作为循环频率,采用不同的循环频率作为多通道循环维纳滤波参数,可以从观测信号中提取出不同类型的故障源信号。

2 基于CCA盲提取的多通道循环维纳滤波器

2.1 多通道循环维纳滤波器

循环维纳滤波器是从观测信号中恢复和分析轴承故障源信号的重要方法,传统循环维纳滤波器采用单一通道观测信号来提取故障源,一般是从多个观测通道中选择某一路观测信号,其故障源信号恢复的效果严重依赖所选择的观测通道,若选择的观测信号包含了较强的故障源分量,那么循环维纳滤波可以给出较好的故障源恢复效果,否则故障源提取一般不准确,尤其对于早期微弱故障诊断,单通道循环维纳滤波往往失效。为了避免循环维纳滤波器对通道选择的依赖性,并提高其对早期微弱故障的诊断能力,提出多通道循环维纳滤波器,其结构框图如图2所示。

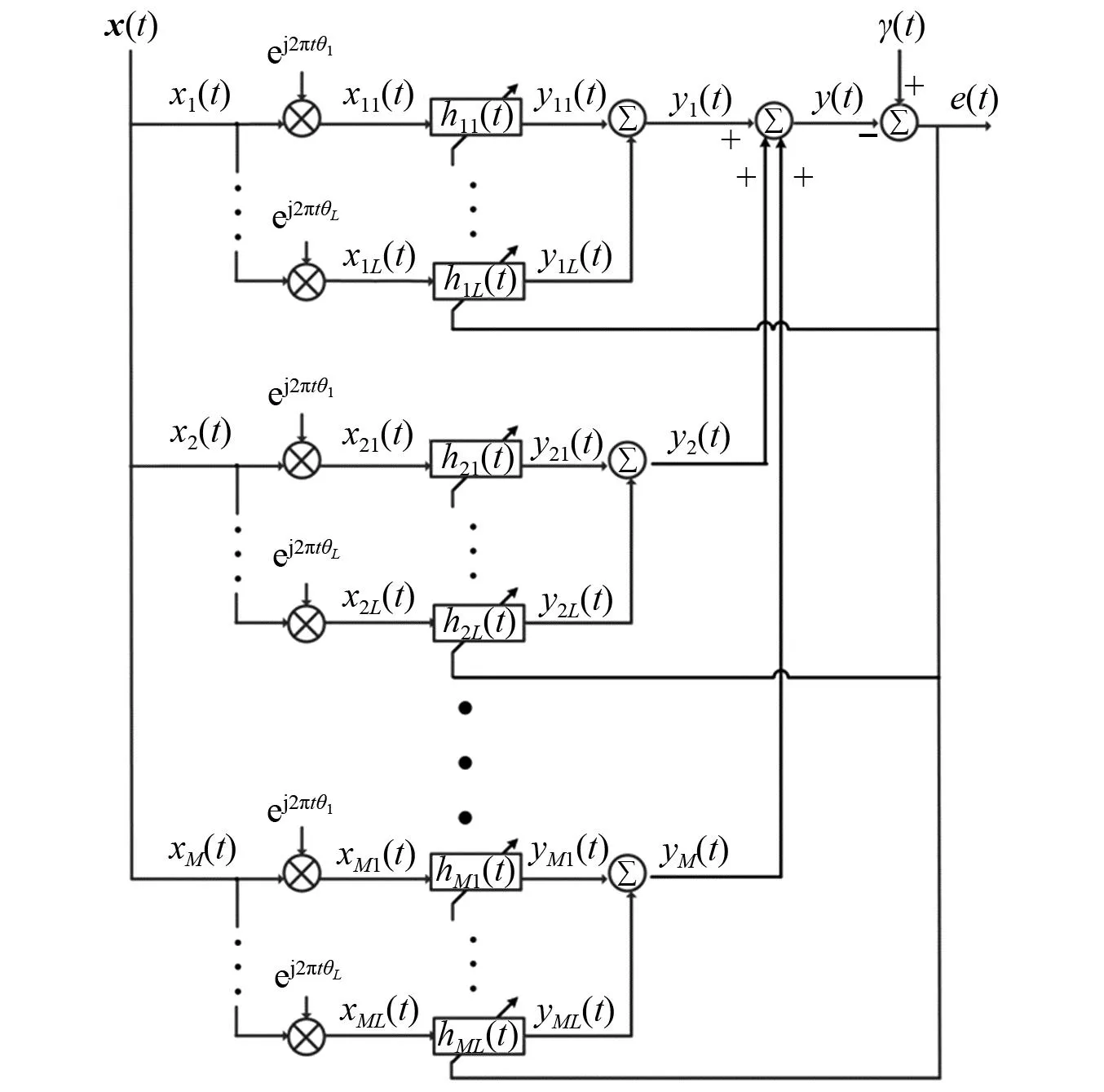
图2 多通道循环维纳滤波器结构框图Fig.2 Block diagram of multi-channel cyclic Wiener filter

以某一故障源信号的提取为例,以下给出多通道循环维纳滤波的工作原理。根据轴承尺寸参数及转速计算故障特征频率f,循环频率取f及其倍频,假定共选择L个循环频率,则第l个循环频率可表示为ql=lf(l={1,…,L})。分别构建M×L个K阶的循环维纳滤波器,将每个观测信号的频移作为滤波器的输入信号。例如,令xm(t)的第l个频移信号表示为xml(t)=xm(t)ej2πθlt,将其输入滤波器hml(t),得到输出信号yml(t),那么第m个通道的滤波输出可通过卷积运算表示为

(6)

对所有通道的输出信号求和,得到多通道循环维纳滤波输出信号y(t)

(7)

令γ(t)表示循环维纳滤波器的期望信号,那么估计误差e(t)为

e(t)=γ(t)-y(t)

(8)

均方误差代价函数可表示为

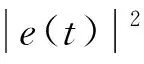
(9)

计算代价函数对滤波器权系数hml(k)的梯度

(10)

那么最优解满足条件

(11)

即循环平稳信号的正交性原理

(12)

式中,〈·〉为时间平均。将式(6)和式(7)代入式(12)得到

(13)

式(13)即为多通道循环维纳-霍夫方程,其中等号左边为滤波器输入信号与期望信号的互相关,等号右边是滤波器输入信号的自相关函数,求解该方程便可完成滤波器参数估计。

由于多通道循环维纳滤波器参数数量庞大,维纳-霍夫方程难以直接求解,本文采用随机梯度下降算法完成滤波器参数的数值优化。令所有滤波器权系数hml(k)形成M×L×K维列向量h(t),其中t为迭代次数,那么h(t)的梯度可表示为∇hJ2={∇hJ2[hml(k)]},则滤波器权系数可按照最速下降的方向更新

h(t+1)=h(t)-μ∇hJ2[h(t)]

(14)

式中,μ为迭代步长。

2.2 期望信号的CCA盲提取方法

期望信号γ(t)的选取对循环维纳滤波器提取结果有很大影响,明阳等提出将观测信号本身作为期望信号,这种方法只适用于轴承的单一故障诊断问题,不适合轴承复合故障诊断问题;郝芳等提出将人工合成的轴承单一故障振动信号作为期望信号,这种方法依赖轴承的先验信息和采样信息,且人工合成的期望信号很可能导致虚假故障的问题。

循环维纳滤波器的期望信号应能表征故障源的特征,且应该来源于采集的振动信号,最合适的期望信号应该是故障特征信号。本文提出CCA盲提取方法,从观测信号中提取故障特征信号。CCA盲提取的基本原理是多个非相干信号的和的自相关不超过单个信号自相关的最大值[22]。令w表示提取向量,可以通过求解以下优化问题得到最优提取向量

(15)

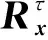
τi=1/fi

(16)

同理,选取不同的时延可以计算不同故障特征信号的提取向量。

d(1)=-∇w(1)J1[w(1)]=-g(1)

(17)

式中:g≜∇wJ1(w)为J1(w)关于W的梯度向量;∇为梯度算子;w(1)为任意给定的提取向量初始值,当t>1时,搜索方向d(t)在当前最速下降方向-g(t)上进行如下修正得到

d(t)=-g(t)+ρ(t-1)d(t-1)

(18)

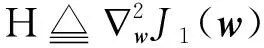
dT(t)H(t-1)d(t-1)=0

(19)

将式(18)代入式(19)可得到

(20)

计算得到搜索方向d(t)后,盲提取向量W按如下公式完成更新

w(t+1)=w(t)+ηtd(t)

(21)

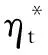
(22)

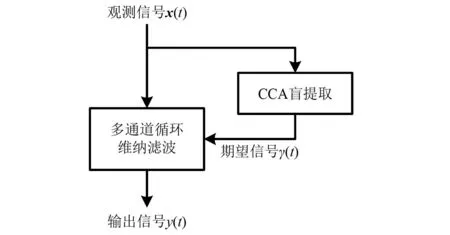
图3 基于CCA盲提取的多通道循环维纳滤波算法总体架构Fig.3 The block diagram of CCA blind extraction based multi-channel cyclic Wiener filter

3 仿真与试验结果

本章分别通过仿真和试验结果验证多通道循环维纳滤波方法在轴承复合故障诊断中的有效性。在第一部分仿真中,故障源信号采用凯斯西储大学提供的轴承振动数据[23],通过随机生成的混合矩阵来模拟不同故障源信号的混合过程。在航发轴承试验机上通过多个振动传感器采集得到复合故障轴承振动信号,分别使用基于CCA盲提取的单通道循环维纳滤波和多通道循环维纳滤波算法提取故障源信号,对比分析轴承复合故障诊断效果。

3.1 仿真结果

在仿真中,故障源采用凯斯西储大学数据中心提供的3种不同类型的单一故障源信号,其中包括内圈故障、外圈故障和无故障的转频信号,选取一路随机产生的高斯白噪声模拟环境噪声。源信号的时域波形和包络谱如图4所示。由图4(b)可知,源信号分别为特征频率为159.7 Hz的内圈故障源信号、特征频率为30.03 Hz的转频信号、特征频率为106.2 Hz的外圈故障源信号和随机生成的高斯噪声信号。

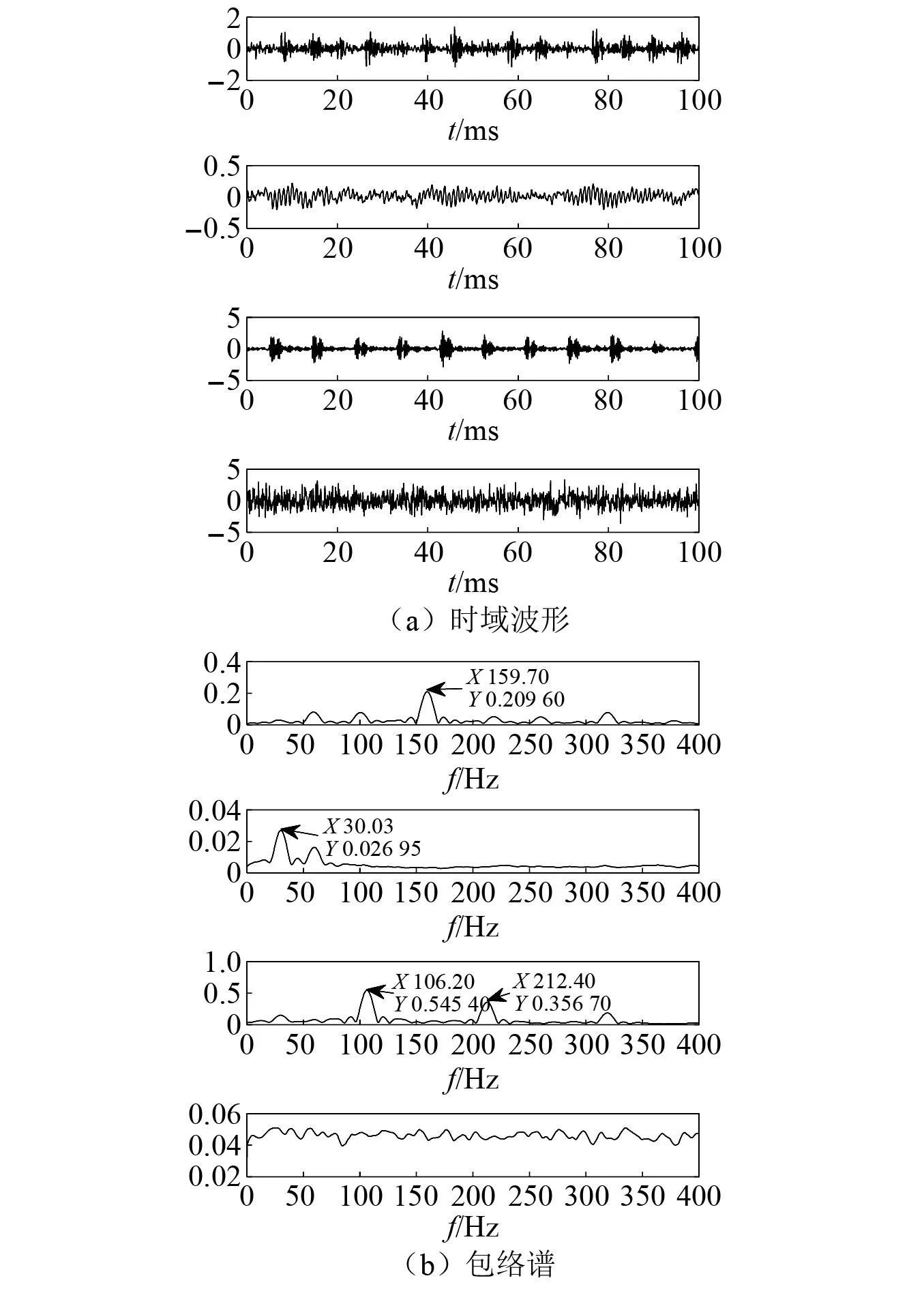
图4 源信号的时域波形和包络谱Fig.4 Time-domain waveform and envelope spectrum of the source signal

通道3观测的信号包络谱,可以看到频率为106.2 Hz的外圈故障频率成分较明显,但故障特征频率为159.7 Hz的内圈故障频率成分几乎被其他信号淹没,因此内圈故障源信号恢复难度更大,如图5(a)所示。将CCA盲提取得到的故障特征信号作为期望信号,单通道循环维纳滤波方法的提取结果,如图5(b)所示。采用提出的基于CCA盲提取的多通道循环维纳滤波方法提取结果,如图5(c)所示。对比发现,两种方法都可以从混合信号中恢复外圈故障源信号。

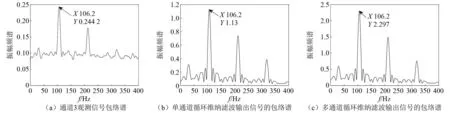
图5 外圈故障源信号提取结果Fig.5 The extraction results of outer ring fault source signal

内圈故障源信号的提取结果如图6所示。其中单通道循环维纳滤波方法提取的故障源信号包络谱(见图6(a));根据包络谱分析,单通道维纳滤波不能从观测信号中提取出内圈故障源信号;采用本文提出的多通道循环维纳滤波方法提取结果包络谱(见图6(b));从包络谱中可以看到故障特征频率为159.7 Hz的内圈故障源信号,与单通道循环维纳滤波方法相比,多通道循环维纳滤波对干扰信号的抑制效果更好。仿真结果说明单通道循环维纳滤波器提取效果严重依赖于观测信号信噪比,观测信号中频率成分较明显的外圈故障源信号提取效果较好,而内圈故障源信号在观测信号中较微弱,提取效果较差,但本文提出的多通道循环维纳滤波克服了这个问题,对内圈和外圈故障源信号都具有较好的提取效果。这是因为布置在不同位置的传感器采集到的观测信号不同,多通道循环维纳滤波利用了所有通道的信息,因此得到了更好的提取效果。

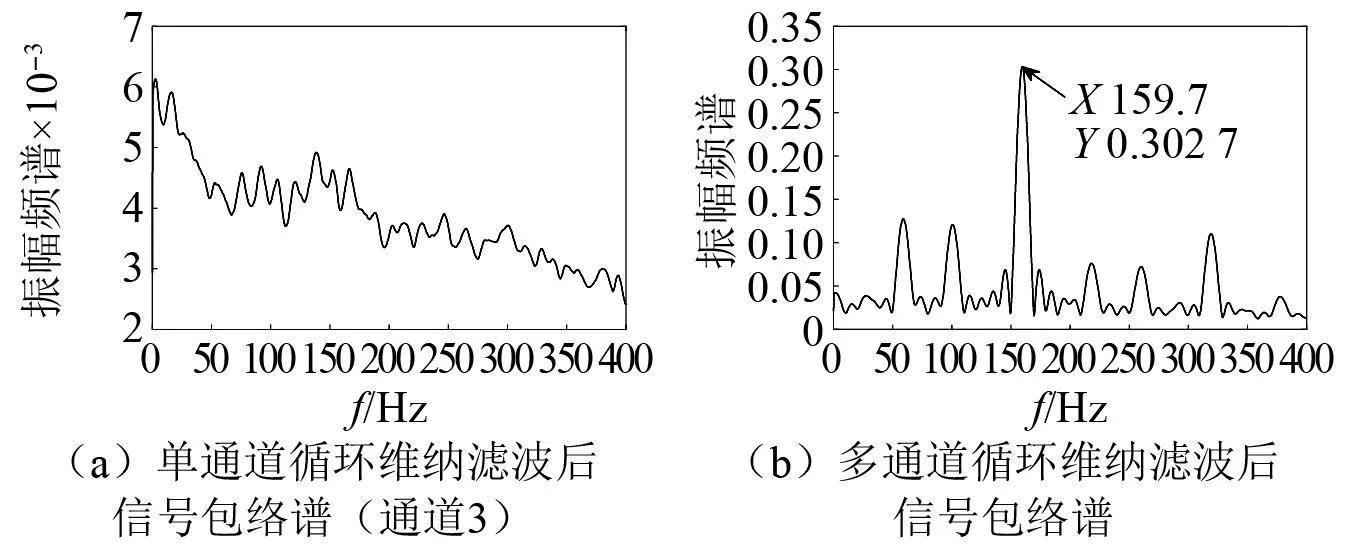
图6 内圈故障源信号提取结果Fig.6 The extraction result of inner ring fault source signal

为了比较提出的CCA盲提取多通道循环维纳滤波算法(记为CCA+MCWF)与传统单通道循环维纳滤波算法(记为SCWF,single channel Wiener filtering)的故障源恢复性能,定义源信号恢复的均方误差为

(23)

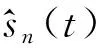
图7 不同信噪比下算法的故障源恢复性能Fig.7 The MSE performance for fault signal recovery under different signal to noise ratios

3.2 试验结果

在试验中,我们使用了型号为D276126NQ1U的双半内圈三点接触球轴承,该轴承是某型号航空发动机中支撑高压压气机的前支点止推轴承,轴承的内圈和外圈上均存在故障点,是一个典型的复合故障轴承,其尺寸参数如表1所示。

表1 轴承尺寸参数Tab.1 Bearing size parameters

通过轴承试验机上布置的8个加速度传感器采集试验轴承的振动信号,其中3个加速度传感器布置在轴承座上,另外5个加速度传感器布置在试验机外壳上,具体布置位置如图8所示。振动信号采样率为20 kHz,根据式(4)和式(5)计算得到轴承故障特征频率,其中内圈故障特征频率为159.9 Hz,外圈故障特征频率为123.4 Hz。采用本文提出的多通道循环维纳滤波从观测信号中恢复单一故障源信号。为了更好的衡量提取效果,试验中定义信号干扰比如下

图8 传感器布置图Fig.8 Sensor layout

SIR=ρs/ρi

(24)

式中:ρs为包络谱中目标故障源信号的幅值;ρi为除去目标故障特征频率成分及其倍频分量后的最大干扰源信号幅值。例如在试验中,观测信号包络谱中主要包含内圈故障源信号和外圈故障源信号,在提取内圈故障源信号时,最大干扰故障源信号为外圈故障源信号,在提取外圈故障源信号时,最大干扰故障源信号为内圈故障源信号。SIR(signal to interference ratio)越大表示对干扰成分的抑制越充分,对目标故障源信号的提取效果越好。分别采用单通道循环维纳滤波方法和多通道循环维纳滤波方法从观测信号中提取故障源信号,分析提取结果包络谱诊断轴承具体部件。

3.2.1 内圈故障源信号提取

分别采用单通道循环维纳滤波方法和本文提出的多通道循环维纳滤波方法提取观测信号中的内圈故障源信号,提取结果如图9所示。其中图9(a)为观测通道1信号包络谱,图9(a)中虚垂线、点垂线和点划垂线分别表示转频、外圈故障特征频率和内圈故障特征频率的理论值,从包络谱中可以看到频率为17.09 Hz的转频信号、频率为159.9 Hz的内圈故障源信号及其附近的频率为143.4 Hz和177 Hz的转频调制信号频率成分、频率为125.1 Hz的外圈故障源信号。内圈故障特征频率附近存在转频调制现象是因为内圈上缺陷的绝对位置会随着轴的转动而周期性变化;图9(b)为单通道循环维纳滤波方法提取结果包络谱,计算得到SIR=2.376;本文提出的多通道循环维纳滤波器采用全部8个通道的观测信号作为滤波器的输入信号,提取结果见图9(c),从包络谱中可以看到频率为159.9 Hz的内圈故障频率成分,计算得到SIR=2.611,与单通道循环维纳滤波方法相比,多通道循环维纳滤波有更好的恢复效果。

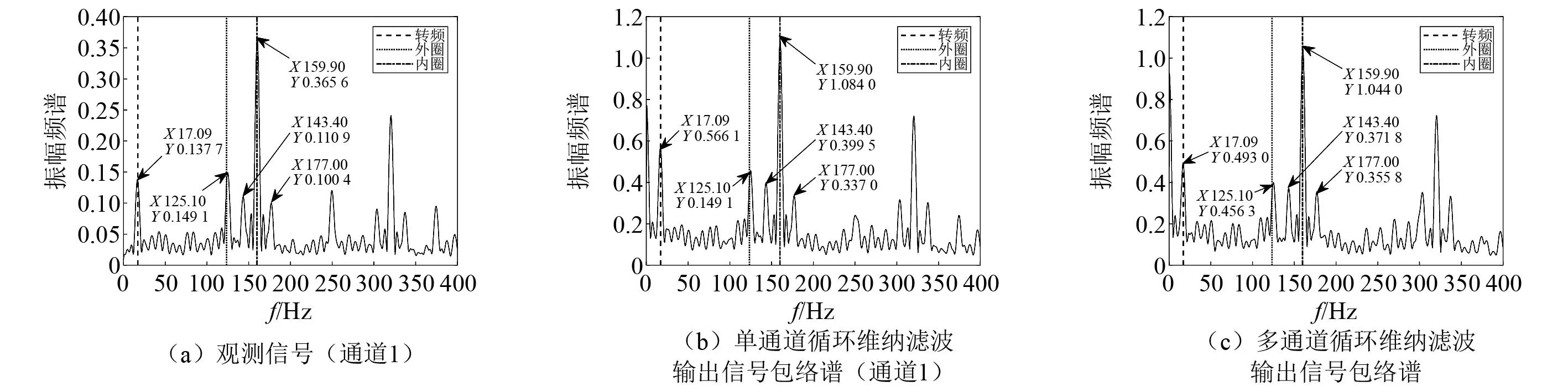
图9 内圈故障源信号提取结果Fig.9 The extraction result of inner ring fault source signal

3.2.2 外圈故障源信号提取

观察图9(a)发现,观测信号中外圈故障源信号的幅值比内圈故障源信号的幅值更小,这说明外圈故障源信号的提取对应着干扰更强的情况,难度更大。在外圈故障源信号提取过程中,首先利用CCA盲提取方法提取外圈故障特征信号,提取结果如图10所示。

图10 CCA提取结果包络谱Fig.10 CCA extraction result envelope spectrum

经过CCA盲提取,频率为125.1 Hz的外圈故障频率成分已被放大,同时频率为159.9 Hz的内圈故障频率成分被抑制,计算得到输出信噪比SIR=1.599。但CCA盲提取得到的故障特征信号包络谱仍较为杂乱,只能作为内圈故障源的初步估计,为了获得更好的恢复效果,采用提出的多通道循环维纳滤波方法进一步恢复外圈故障源信号。

采用图9(a)所示的观测通道1信号作为单通道循环维纳滤波器的输入信号,提取结果的包络谱如图11所示。从图11可知,经过单通道循环维纳滤波后,外圈故障源恢复效果得到提升,计算得到SIR=2.513。

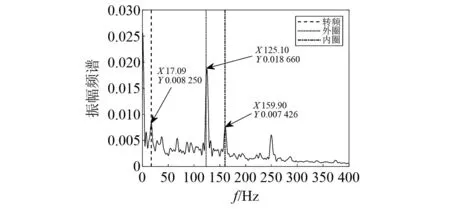
图11 单通道循环维纳滤波输出信号包络谱(通道1)Fig.11 Signal envelope spectrum after single-channel cyclic Wiener filter (channel 1)

观测通道4信号的包络谱,如图12(a)所示。由包络谱可知,频率为125.1 Hz的外圈故障频率成分几乎消失,将其作为单通道循环维纳滤波器输入信号,提取外圈故障源信号结果如图12(b)所示。由图12(b)可知,使用通道4的观测信号,单通道循环维纳滤波方法已经失效。对比图10和图11(b),可以发现单通道循环维纳滤波方法提取外圈故障源信号时,提取效果严重依赖观测信号的信噪比,其中图9(a)的观测通道1信噪比高,含有明显的外圈故障频率成分,对应于图11中故障源信号恢复效果较好,而图12(a)的观测通道4信噪比低,外圈故障频率成分及其微弱,对应于图12(b)故障源信号恢复效果差。因此若观测信号信噪比低,那么单通道循环维纳滤波将失效。提出的多通道循环维纳滤波器将全部8个通道观测信号作为输入信号,提取结果如图13所示。由图13可知,故障特征频率为125.1 Hz的外圈故障源信号成分,计算得到SIR=2.562,表明其他干扰源被有效抑制。

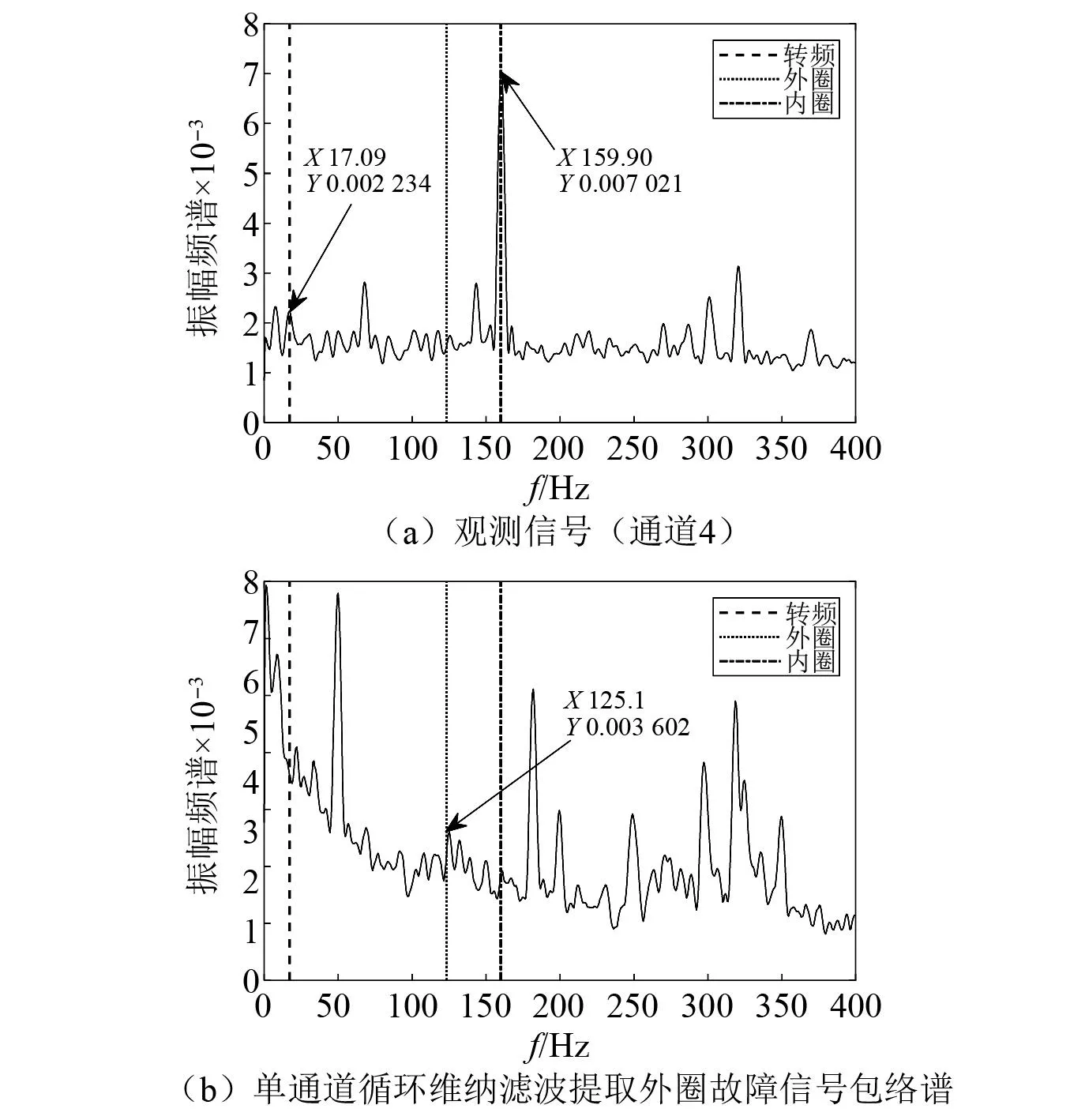
图12 外圈故障源信号提取结果(通道4)Fig.12 The extraction results of outer ring fault source signal (channel 4)

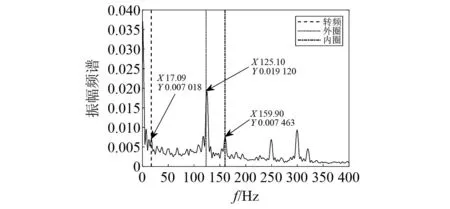
图13 多通道循环维纳滤波输出信号包络谱Fig.13 Signal envelope spectrum after multi-channel cyclic Wiener filter

为了进一步定量说明提出算法的故障源恢复性能,对内外圈复合故障轴承,在轴承试验机上采集了多个不同转速下的振动数据,试验机径向载荷固定为2.5 kN,轴向载荷固定为4 kN,转速范围为1 000～2 000 r/min,转速步进量为100 r/min,共设10个转速,每个转速上采集10组数据,每组数据时长1 s,共得到100组复合故障数据。将提出的方法(CCA+MCWF)与SCWF、经验模式分解(empirical mode decomposition,EMD)、变分模态分解(variational mode decomposition,VMD)和快速变分模态分解(fast variational mode decomposition,FVMD)等方法进行了性能比较,其中提出的算法使用8个通道的观测数据,其他算法均为单通道分析算法,均使用信噪比较高的通道1观测数据。

以上方法对100组数据进行内外圈故障分析的平均SIR性能,如表2所示。综合对比几种方法的SIR性能可以看出,对于内圈故障源的提取,几种方法均能有效抑制其他干扰成分,而对于外圈故障源的提取,几种方法的干扰抑制性能差别较大,SCWF几乎不能提取目标故障源信号,EMD,VMD和FVMD的干扰源抑制不充分,导致目标故障源恢复效果一般,而无论对于内圈还是外圈故障源的恢复,提出的方法都给出了最佳的SIR性能,这主要是由于两个方面的原因:一方面,通过CCA盲提取可以获得目标源信号的一个较好的初步估计,以此作为循环维纳滤波的期望信号,消除了对高信噪比观测数据的依赖;另一方面,提出的方法采用多通道观测数据,故障特征的提取是在多个通道数据间自适应加权实现的,提高了故障源恢复的可靠性。

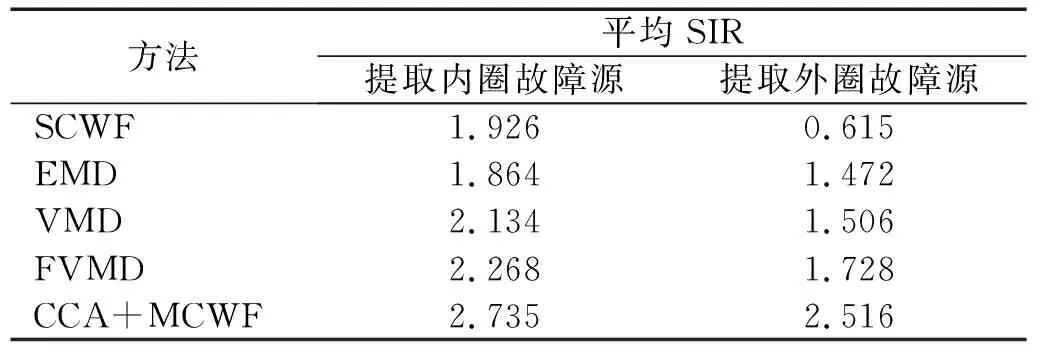
表2 不同方法对内外圈复合故障分析的平均性能比较Tab.2 Averaged performance of five competitors for inner and outer race compound fault analysis

4 结 论

针对低信噪比和强干扰下的轴承复合故障诊断难题,提出了一种基于CCA盲提取的多通道循环维纳滤波轴承故障分析方法,将CCA盲提取得到的故障特征信号作为多通道循环维纳滤波器的期望信号,从而恢复故障源信号,通过对故障源信号的包络谱分析完成轴承复合故障诊断。仿真和试验结果可以得出以下结论:

(1)使用CCA盲提取得到的故障特征信号作为期望信号,避免了现有方法的诊断效果严重依赖于轴承参数和信号采样参数的问题。

(2)单通道循环维纳滤波方法仅在信噪比较高时有效,而提出的多通道循环维纳滤波方法充分利用了观测信号中所有通道信息,自适应调整各通道权重,即使在低信噪比下也可以获得较好的故障源恢复效果,提高了故障诊断的可靠性。

鉴于航空发动机对其部件的高可靠性要求,获取缺陷轴承的发动机振动数据相当困难,论文仅利用了轴承试验机数据验证了算法的可行性和性能提升,由于试验机和航空发动机主轴承支承结构的差异较大,论文建立的信号模型虽有一定的普适性,但算法在实际工程中的轴承故障分析性能仍需进一步验证。