支座激励下端部带水平减震装置悬索的动力分析

张 鹏, 王国威, 卢文胜, 周 祺

(1. 江西理工大学 土木与测绘工程学院, 江西 赣州 341000; 2. 同济大学 土木工程防灾国家实验室, 上海 200092)

将索网幕墙直接支承在两相邻结构上,形成以两相邻结构为主结构、中部索网幕墙为次结构的新体系,是近年来索网幕墙结构应用的新发展,典型的工程案例有北京融科C座[1]、北京土城电话局[2]、天津国际金融酒店大厦[3]以及福州东部新城大厦[4]等。在地震激励作用下,索网结构需要承担两相邻结构的相对位移输入,可能引起索网结构出现断裂、松弛或变形[5],带来安全隐患。为此,有必要采用减震措施提升索网幕墙结构的抗震性能。

关于索网幕墙的抗震性能,由于其质量轻、刚度柔,直接地震响应较小。振动台试验研究表明[6-7],其地震响应主要以对称振型为主,且以第一阶振型占主要成分,索网幕墙具有较好的抗震性能,可以在地震烈度较高的地区使用。但当索网幕墙依附于建筑主体结构时,地震作用下主体结构的变形可能会引起其破坏。为了减小主体结构变形输入引起索网幕墙的响应,李明等[8-9]提出了两种拉索保护装置,分别为拉索弹簧缓冲装置和防破断装置,通过在拉索端部串联保护装置来减轻主结构对索网的影响,并应用在实际工程中。李明等对附加索端弹簧装置悬索的静力性能进行了研究,张鹏等[10-11]对动力荷载作用下附加弹簧装置悬索的动力特性和动力响应进行研究,研究表明该装置可明显降低拉索的索力,但是相应的变形会增大。

在减轻爆炸荷载及风荷载作用下索网幕墙的动力响应研究方面,Bcdon等[12-13]提出由线性弹簧和摩擦阻尼器串联组合的新型摩擦耗能装置,被安装在拉索端部,实现减轻爆炸荷载下的振动,然而,一旦摩擦阻尼器滑动,索网很难恢复到原来的位置。Dos Santos等[14]提出了一种新型的主动控制系统,该系统可减轻玻璃面板在爆炸荷载下的应力以及能使索网恢复到初始状态。Gong等[15-16]开发了一种具有可变阻尼的半主动摩擦连接器,可以控制系统改变摩擦装置的法向力,通过改变装置阻尼力实现对风振响应的控制。Khalkhaliha等[17]提出在拉索端部设置智能滑动支座,通过控制支座位移来改变索力大小,实现平面索网幕墙风振响应的主动控制。但是以上主动或半主动的减振方法需要复杂的控制装置和能量输入,被动减振技术装置简单,可靠性较高,应进一步研究索网幕墙被动控制技术。

针对相邻结构间单向索采光顶,为了减轻地震作用下悬索的地震响应,本文提出在悬索端部附加水平减震装置(包括弹簧装置和弹簧阻尼装置)来减小单索的地震响应,弹簧装置可以减少单索的地震输入而阻尼装置可为结构提供附加阻尼。悬索是该幕墙体系的基本受力单元,通过推导端部带减震装置悬索结构的动力方程,得到结构频率和模态阻尼比计算公式,分析结构阻尼特性,通过开展支座激励下附加水平减震装置悬索的动力响应试验,验证该装置的减震效果。本文的研究将为此类新型装置在单索幕墙工程应用提供参考依据。

1 端部带水平减震装置悬索的动力分析模型与试验验证

1.1 动力方程的建立与求解

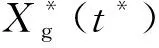
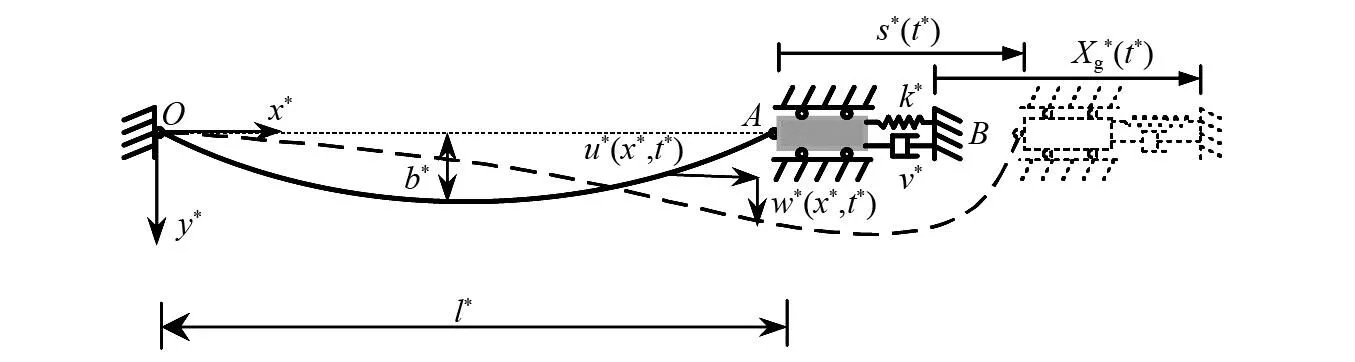
图1 端部带水平减震装置悬索的分析模型Fig.1 Analysis model of cables with horizontal mitigation devices

悬索平面内的动力方程如式(1)和式(2)所示[18]。

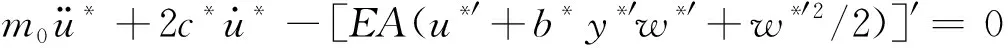
(1)

[H*w*′+EA(b*y*′+w*′)(u*′+b*y*′w*′+w*′2/2)]′

(2)

边界条件如下所示。

(1) 悬索在O点处的水平和竖向位移为0,悬索在A点处的竖向位移为0,表示如下

u*(x*,t*)|x*=0=w*(x*,t*)|x*=0=w*(x*,t*)|x*=l*=0

(3)

(4)

(3)A点处的力平衡条件如下

(5)

(6)

假定无量纲参数

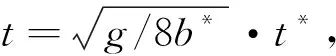
式中:γk为弹簧刚度与悬索线刚度的比值,定义为减震装置的刚度系数;v为减震装置的阻尼系数。

将式(3)～式(6)及无量纲参数代入式(1)和式(2),得到考虑端部带水平减震装置的悬索动力方程和边界条件方程分别如式(7)和式(8)所示。

(7)

(8)

为求解结构自由振动的频率和模态阻尼比,将动力方程式(7)和边界条件方程式(8)的荷载项、结构阻尼项以及非线性项删除,可以得到结构的线性自由振动方程和边界方程分别如式(9)和式(10)所示。

(9)

(10)

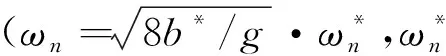
(11)

φn(x)=κn[1-cos(ωnx)-tan(0.5ωn)sin(ωnx)](12)

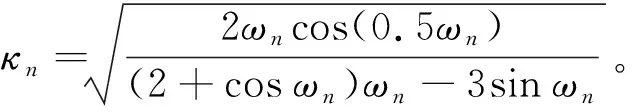
式(11)为复数公式,计算出的对称振型频率值也是复数,可以表示为式(13),复频率的实部和虚部数值分别表示为实数pn和qn。由式(11)可知,结构的复频率主要与悬索动力特征系数αb2、刚度系数γk及阻尼系数ν有关,因此,确定该3个无量纲参数为控制悬索振动的关键参数。

ωn=±pn+iqn

(13)

当该频率计算出后,可以直接计算振型的模态阻尼比,模态阻尼比的计算如式(14)。

(14)

1.2 频率及模态阻尼比公式的试验验证

进行端部带减震装置悬索的自由振动试验,检验频率和模态阻尼比计算公式的正确性。试验分为两步:①进行减震装置的滞回性能试验,得到装置的恢复力模型;②对减震悬索进行自由振动试验。

(1) 减震装置试验

减震装置由线性弹簧和黏滞阻尼器并联组成如图2(a)所示。力学简图如图2(b)所示。为更好的模拟理论模型,减震装置采用线性弹簧和线性阻尼。选择两种规格线性弹簧[19]:①弹簧K1的线圈直径为30 mm,弹簧中径为140 mm;②弹簧K2的线圈直径为35 mm,弹簧中径也为140 mm。装置的阻尼由多个黏滞阻尼器并联组成,单个阻尼器的最大出力为2 kN,最大行程为±25 mm。试验按正弦位移加载,加载幅值取5 mm,8 mm,10 mm和12 mm。加载频率取0.3 Hz,0.5 Hz和0.8 Hz 3种,每级荷载加载3个循环。

图2 减震装置Fig.2 Horizontal mitigation devices

弹簧K1和弹簧K2(以下称弹簧减震装置)在加载频率为0.3 Hz,典型的力-位移恢复力曲线如图3(a)所示。其恢复力与位移关系基本上为线性关系。阻尼装置在0.7Hz加载频率下的典型恢复力曲线如图3(b)所示。滞回曲线呈现“类椭圆形”形状。弹簧装置和阻尼器并联装置(以下称弹簧阻尼减震装置),典型的力-位移恢复力曲线,如图3(c)所示。由图3(c)可知,与弹簧减震装置相比,弹簧阻尼减震装置的滞回曲线呈现“梭形”,有明显的滞回耗能面积,具有耗能能力;与黏滞阻尼的滞回曲线呈现“类椭圆形”相比,弹簧阻尼减震装置有更大的刚度。因此,该装置不仅可以实现较大的刚度同时也具有较好的耗能能力。

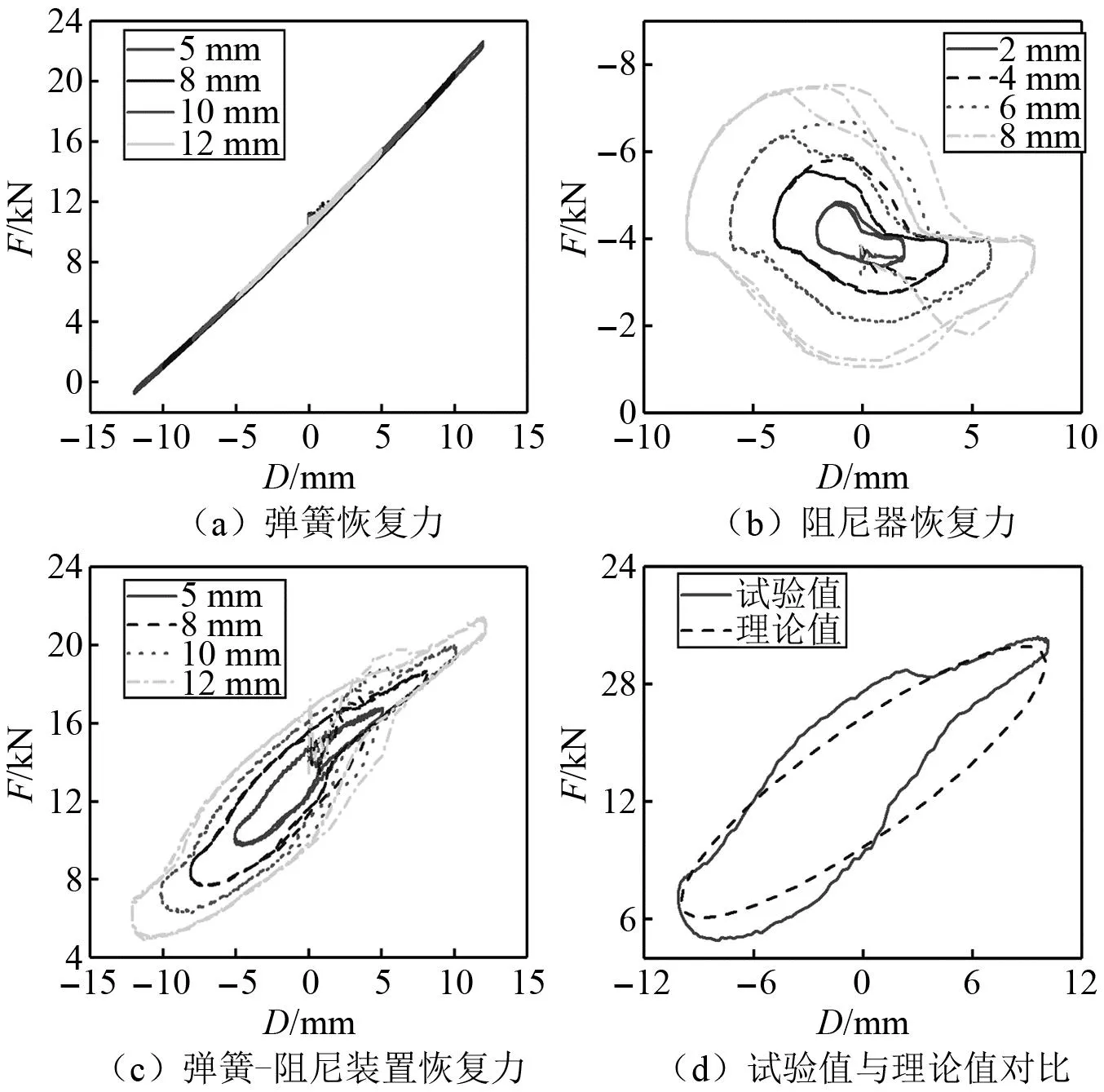
图3 减震装置的恢复力模型Fig.3 Hysteretic model of mitigation devices

采用理想黏弹性模型来模拟减震装置的理论模型,减震装置恢复力F(t)计算公式如式(15)所示。

F(t)=KAsin(2πft)+2πcfAcos(2πft)

(15)

式中:K为弹簧刚度;c为阻尼器的黏滞阻尼系数;A为加载幅值;f为加载频率。

通过试验数据拟合得到弹簧K1和弹簧K2的刚度分别为609 kN/m和965 kN/m,单个阻尼器的黏滞阻尼系数为17.6 kN(s/m)。装置的理论计算值与试验对比,如图3(d)所示。装置的理论计算值和试验值较吻合。

(2) 自由振动试验

端部带减震装置悬索的自由振动试验装置,如图4所示。试验采用M10钢丝绳索,横截面积为59.69 mm2,弹性模量为1.35×105MPa。减震装置两端分别与滑动构架1和滑动构架2相连接。悬索一端与滑动构架2连接,另外一端固定在反力墙上。在悬索上放置配重块,使得悬索具有一定的垂度。将滑动构架1固定,滑动构架2可在导轨上自由滑动。试验开始在悬索中部施加一定的初位移,而后让悬索自由振动。在悬索的两端布置了力传感器以监测索力,在悬索的1/3,1/2和2/3跨处及减震装置两端布置位移计。

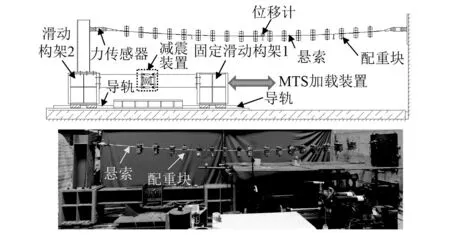
图4 支座激励下端部带减震装置悬索的加载装置Fig.4 Loading equipment for the suspended cable with mitigation devices under support excitation

由式(11)可知,控制体系动力特性的3个主要参数分别为:悬索的动力特性系数αb2、弹簧刚度系数γk及端部阻尼系数ν,通过悬索上的荷载、弹簧刚度以及阻尼器的数量来实现该三控制参数的变化,试件参数如表1所示。悬索的初始张拉力均为24 kN,工况1～工况7悬索上的线荷载为0.256 kN/m,静载作用下悬索的跨中变形为0.08 m,垂跨比b约为1/94,动力特性系数αb2为0.04。工况8～工况14悬索上每米的荷载为0.567 kN/m,静载作用下悬索的跨中变形为0.168 m,垂跨比约为1/45,αb2为0.17。

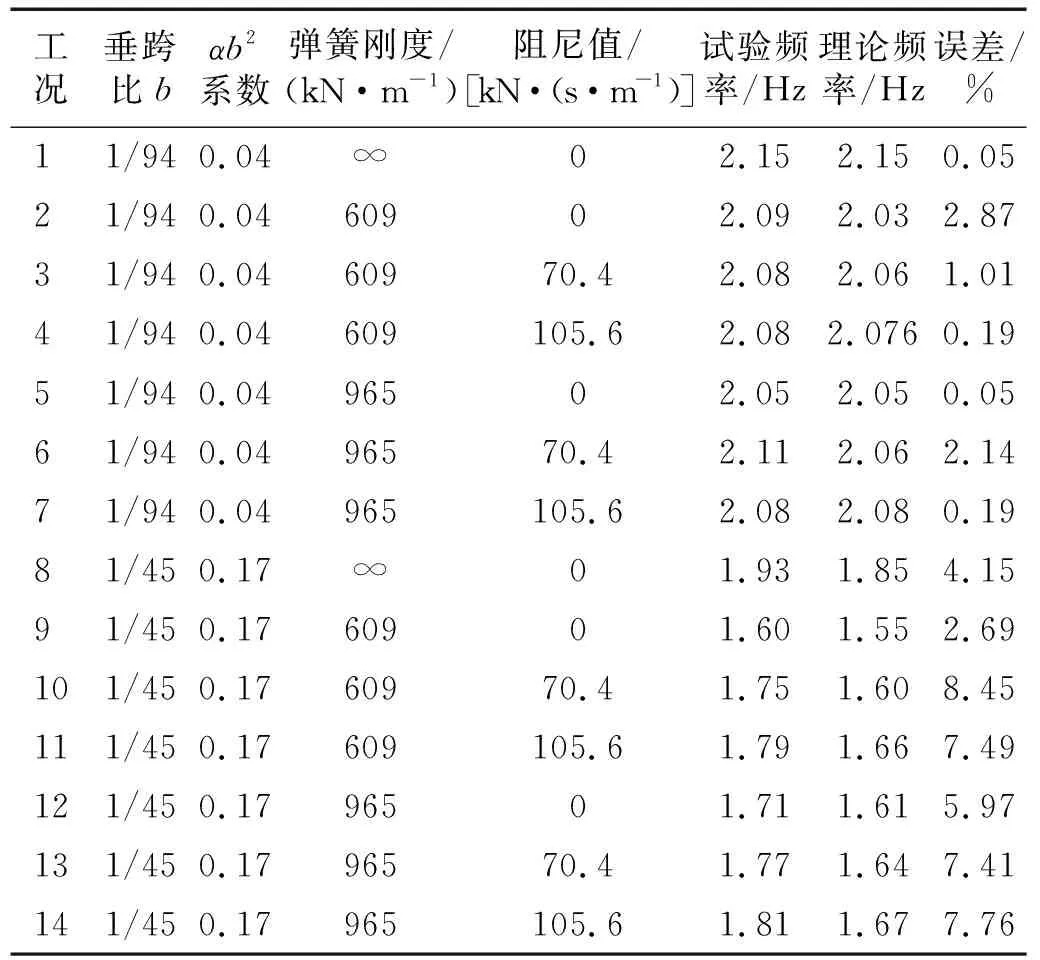
表1 自由振动试验参数及结果表Tab.1 Parameters and results of free vibration test

1.3 理论公式与试验对比

典型悬索的自由振动时程曲线及其频谱如图5所示。各工况频率的试验值和由式(11)计算的理论值之间的误差见表1,对于较小垂度的悬索工况,理论值与试验频率值误差非常小,均小于3%,对于较大垂度的悬索工况,3种方法计算的频率误差也基本小于8%。总体上看,采用理论公式计算的悬索频率值与试验值基本可以吻合,验证了理论计算公式的正确性。

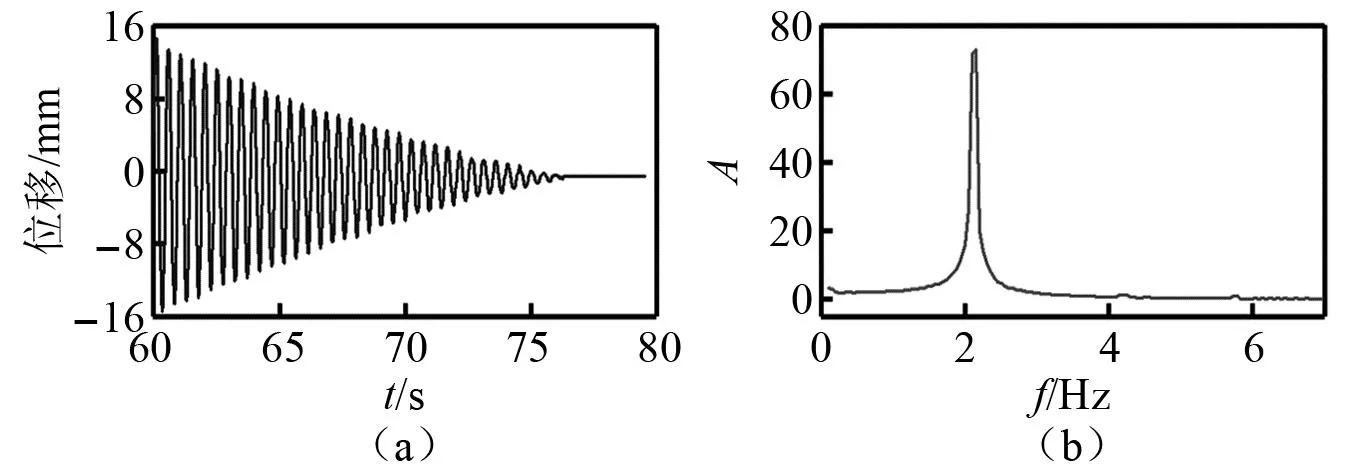
图5 悬索跨中位移时程及频谱曲线Fig.5 Time history and frequency spectrum curve of mid span displacement of suspension cable

2 端部带水平减震装置悬索的阻尼特性分析

在斜拉桥索的减振研究中,常通过分析模态阻尼比来确定阻尼器的贡献。Yoneda等[20]使用数值方法来确定悬索-阻尼器系统的最佳模态阻尼,并发现最优阻尼与阻尼器和悬索锚固端的距离有关。Krenk[21]通过解析法推导了悬索-阻尼器系统的模态阻尼比与附加阻尼系数的解析公式。本部分将基于复频率计算公式式(11),分析悬索的阻尼特性。

2.1 关键参数对悬索频率和模态阻尼比的影响

我国JGJ 257-2012《索结构技术规程》[22]要求悬索结构垂跨比的变形限值为1/50,对应于悬索动力特性系数αb2假定小于0.34。以下将分析3个关键参数对悬索的频率和模态阻尼比的影响。

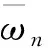
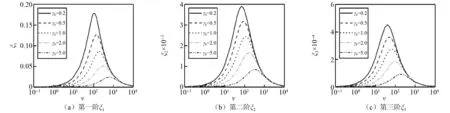
图6 当αb2 =0.24时,γk和ν对模型阻尼比ξn的影响Fig.6 Effect of γk and ν on modal damping ratio ξn when αb2 =0.24

图7 当αb2 = 0.24时,γk和ν对无量纲频率的影响Fig.7 Effect of γk and ν on frequency when αb2 =0.24

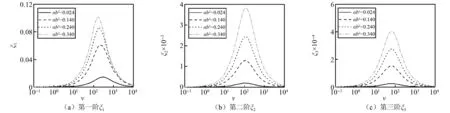
图8 当γk=1时,αb2和ν对模型阻尼比ξn的影响Fig.8 Effect of γk and ν on the modal damping ratio ξn when γk=1

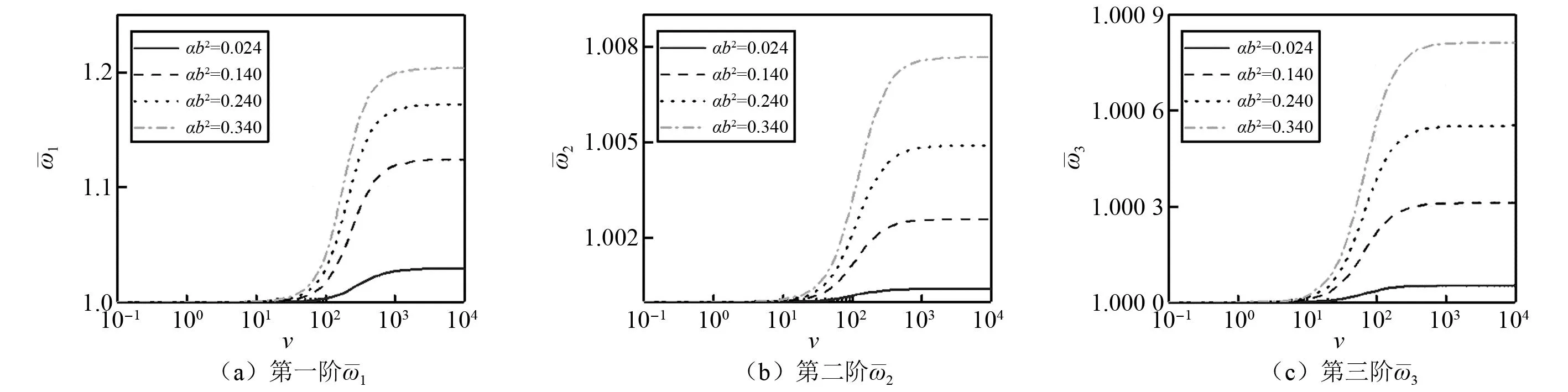
图9 当γk=1时,αb2和ν对无量纲频率的影响Fig.9 Effect of γk and ν on the frequency when γk=1

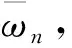
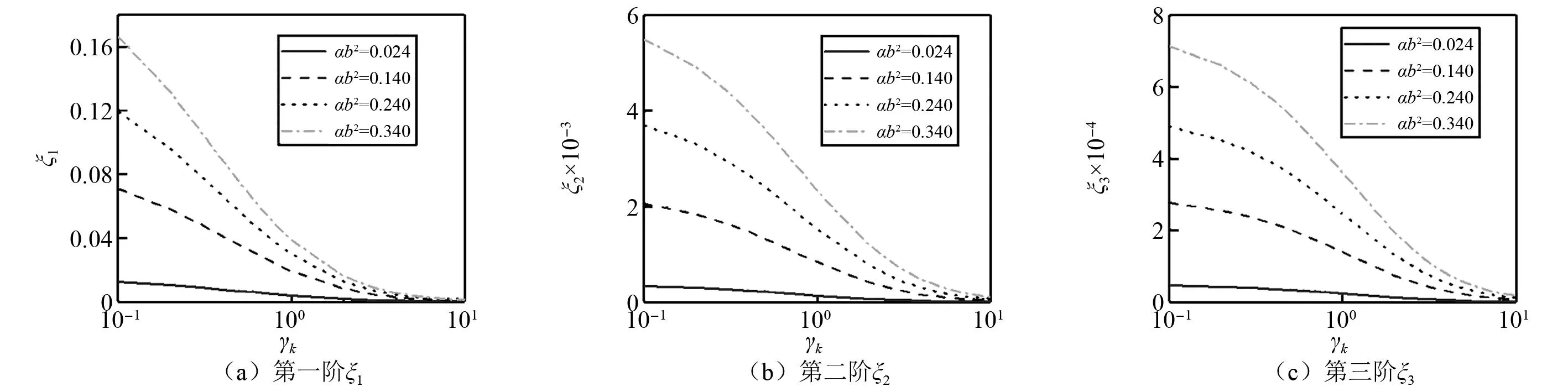
图10 当ν=40时,γk和αb2对模型阻尼比ξn的影响Fig.10 Effect of γk and αb2 on the modal damping ratio ξn when ν=40

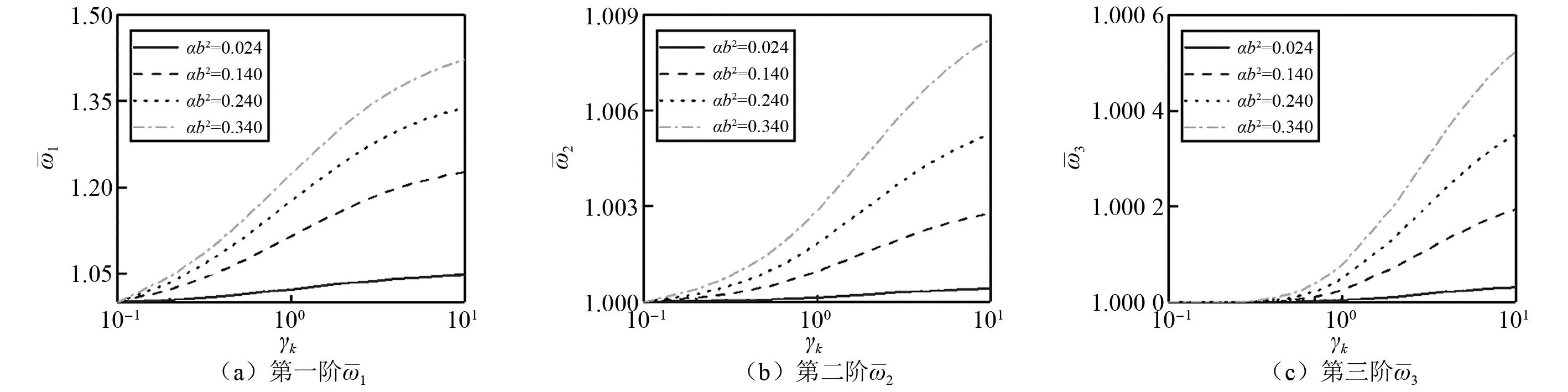
图11 当ν=40,γk和αb2对无量纲频率的影响Fig.11 Effect of γk and αb2 on the frequency when ν=40

2.2 关键参数的建议取值范围

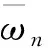
3 支座激励下端部带水平减震装置悬索的动力响应分析

为进一步检验减震效果,进行支座激励下端部带减震装置悬索的动力试验研究。加载装置见图4,通过液压伺服作动器加载装置对悬索施加支座激励,按正弦位移曲线进行加载,加载位移时程为U(t)=Asin(2πft),其中:A为加载位移幅值;f为加载的频率。加载工况如表2所示。刚度系数γk及阻尼系数ν均满足建议取值范围。可分别按下式计算

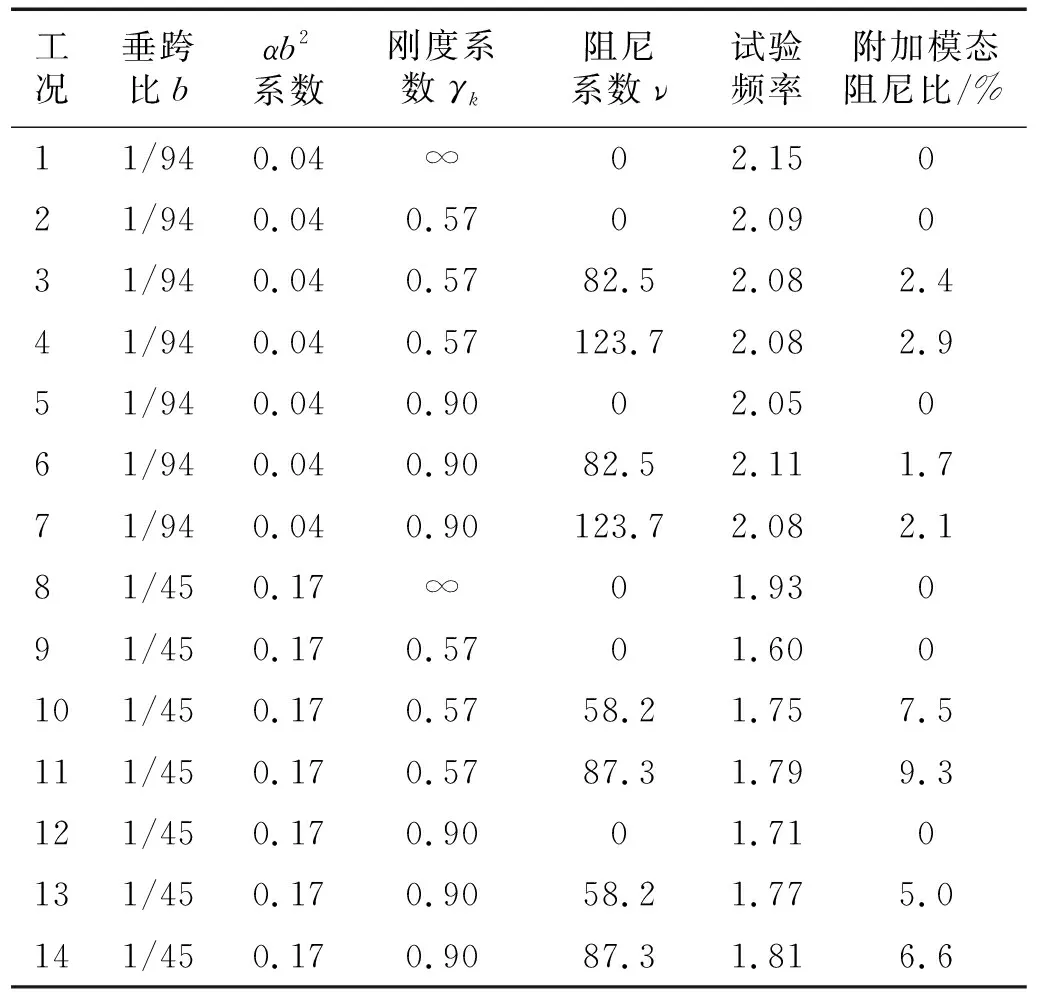
表2 支座激励动力试验工况Tab.2 Dynamic test parameters of support excitations

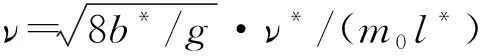
3.1 刚度系数γk对悬索响应的影响分析

选择端部不带阻尼的工况1、工况2、工况5、工况8、工况9、工况12为分析对象,研究刚度系数γk对支座激励下悬索动力响应的影响。共有4种加载制度,分别为:① 幅值A=12 mm,频率f=0.5 Hz; ②A=5 mm,f=0.5 Hz; ③A=5 mm,f=1 Hz; ④A=5 mm,f=1.2 Hz。每种加载制度循环30次。定义动位移ΔD为一次加载中悬索最大位移Dmax与最小位移Dmin之差,反映位移的变化量。动索力ΔF为最大索力Fmax与最小索力Fmin之差,反映索力的变化量。在各种加载制度下,各工况悬索的位移和索力响应如表3所示。δD定义为动位移减震率,为减震工况相对于对应未减震工况(工况2和工况5对应于工况1,工况9和工况12对应于工况8)的动位移减少率。同理,δF为动索力减震率,为减震工况相对于对应未减震工况的动索力减少率。4种加载工况下悬索动力特征系数αb2为0.04的索力和位移时程,如图12和图13所示。由图表可知:

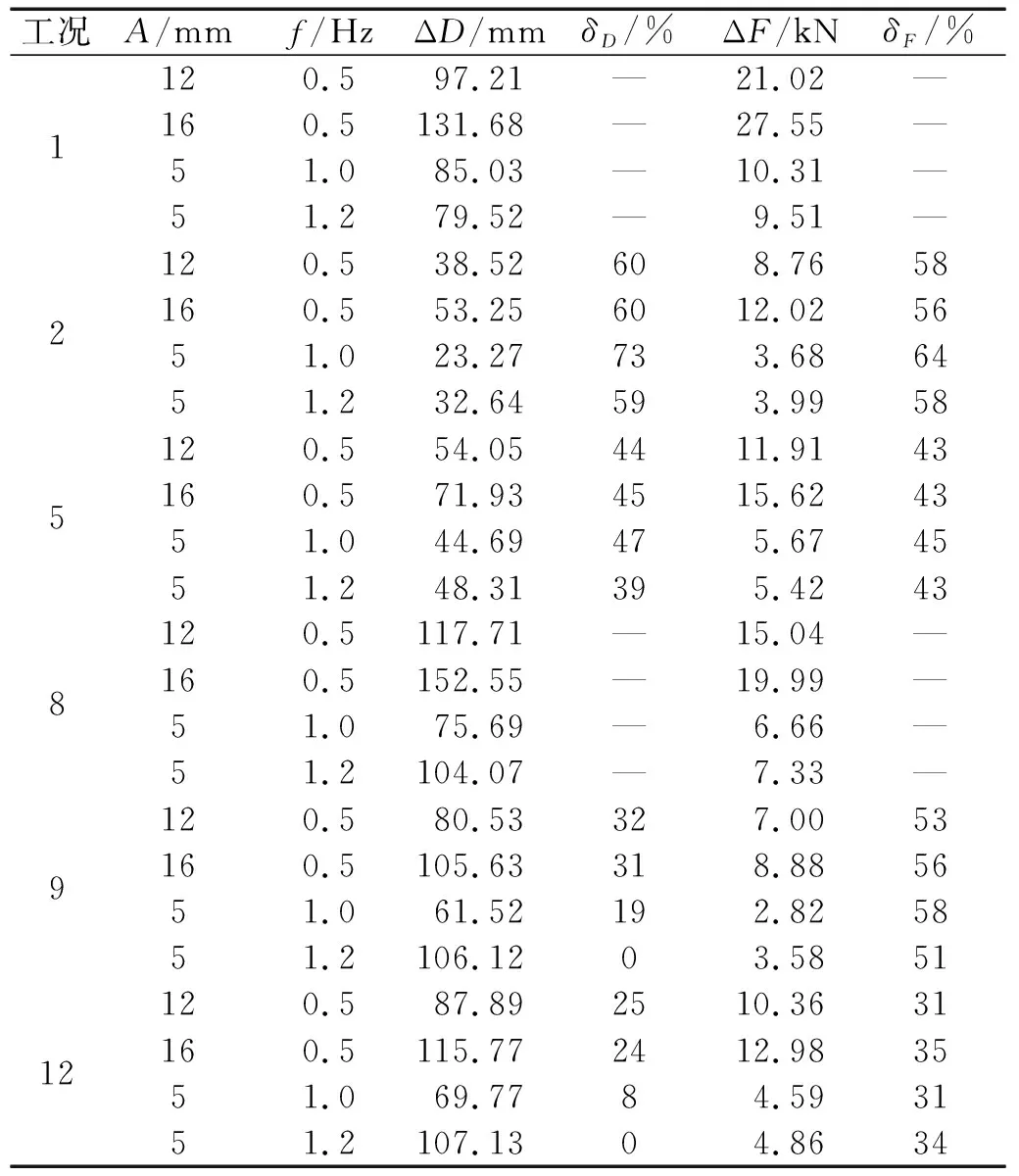
表3 不同端部约束条件下悬索的位移和索力响应Tab.3 Displacement and force of the cable under different end conditions

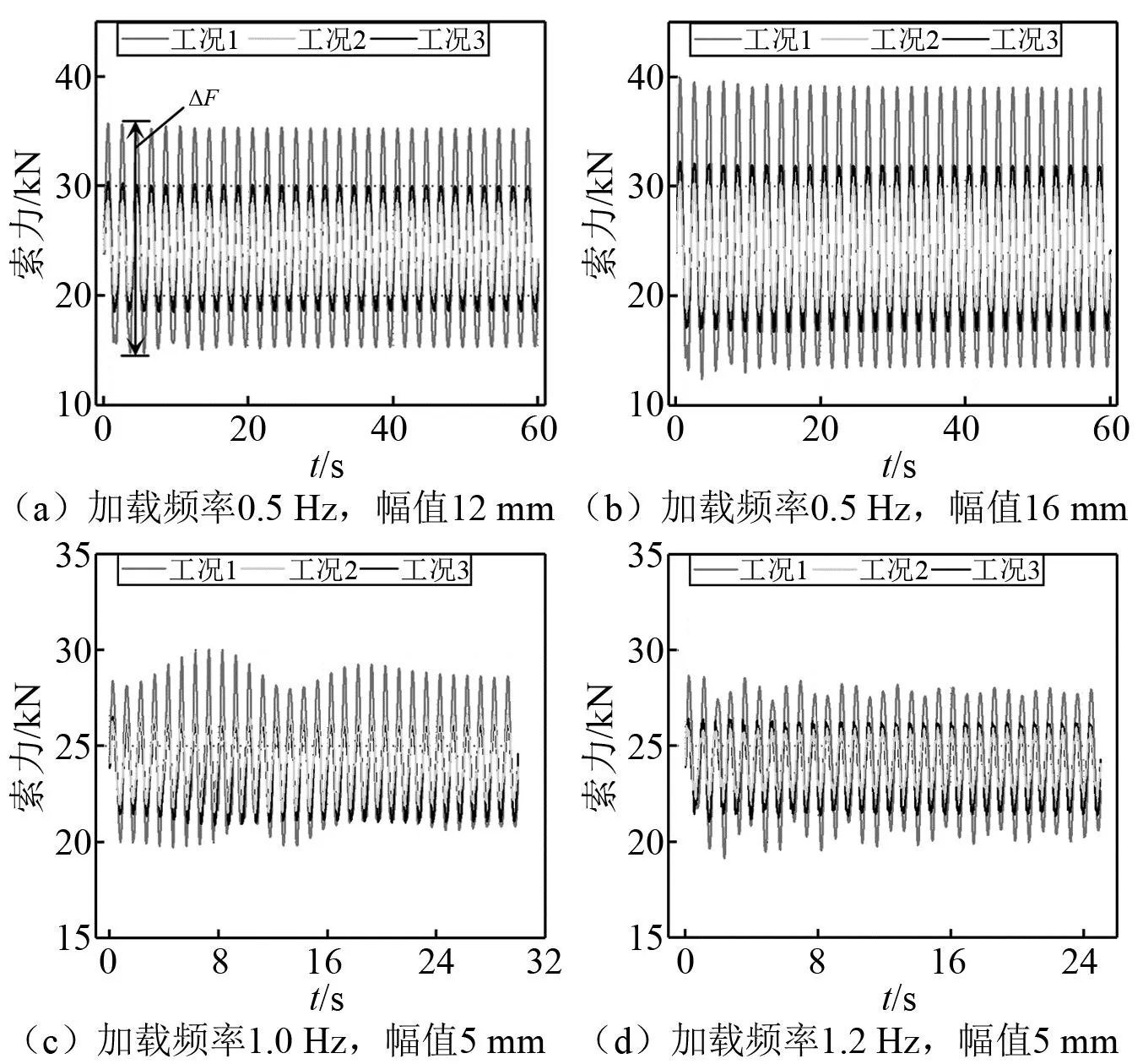
图12 αb2 为0.04悬索索力响应Fig.12 Force response of the cable with αb2=0.04

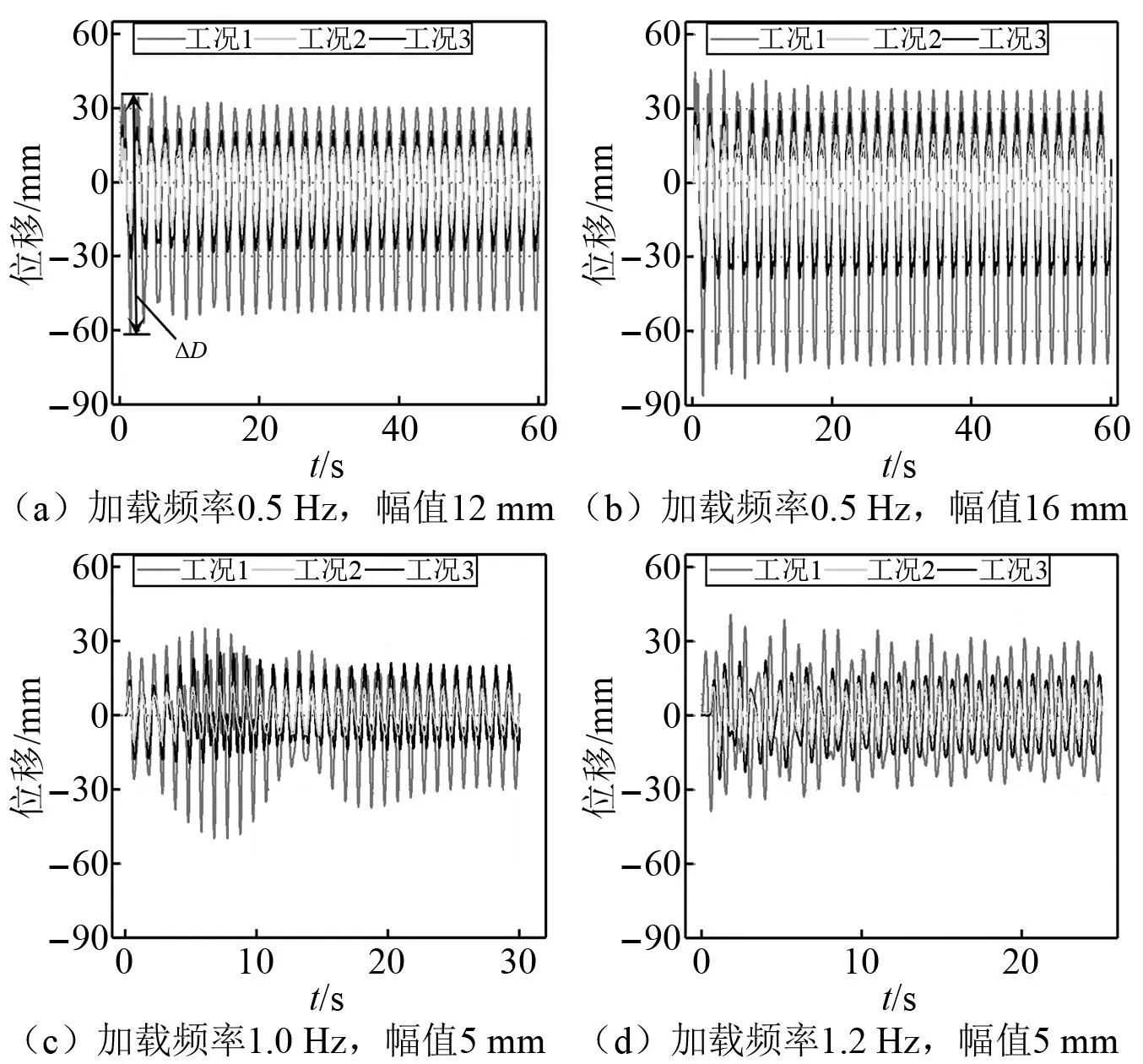
图13 αb2 为0.04悬索位移响应Fig.13 Displacement response of the cable with αb2=0.04

(1) 相同加载条件下,端部带弹簧装置的减震工况2和工况5,工况9和工况10基本上均比未减震工况1,工况9的动位移和动索力更小,反映了端部弹簧装置可以有效降低支座激励下悬索的位移和索力响应。

(2) 刚度系数γk越小,支座激励作用下悬索的动位移和动索力的减震率越大,其原因为刚度系数越小,弹簧变形能力越强,吸收支座变形的能力越强,从而悬索的动位移和索力也越小。例如,如表3所示,刚度系数γk为0.9的工况5比工况1在4种加载条件下的δD为44%,45%,47%和39%,δF分别为43%,43%,45%和43%。而刚度系数为0.57的工况2的δD为60%,60%,73%和59%,δF为58%,56%,64%和58%,动位移和动索力的减震率大于工况5。

(3) 随着激励频率接近悬索的一阶自振频率,弹簧减震装置对悬索的动位移减震性能减低,对动索力减震性能影响不大。例如,工况5的一阶频率为2.05 Hz,在激励频率为1 Hz时的δD和δF分别为47%和45%,而在1.2 Hz时减震率分别为39%和43%;工况9的一阶频率为1.6 Hz,在激励频率为1 Hz的δD和δF分别为19%和58%,在1.2 Hz时减震率分别为0和51%。

3.2 悬索动力特征系数αb2对悬索响应的影响

选择工况1、工况2、工况5、工况8、工况9、工况12为分析对象,研究悬索动力特征系数αb2对悬索响应的影响。由表3可知:

(1)在相同的激励条件和端部约束条件下,悬索动力特征系数αb2越小,悬索的动位移越小,但是动索力越大。例如在加载幅值为12 mm时,工况1的动位移和动索力分别为97.21 mm和21.02 kN,而工况8的动位移和动索力分别为117.9 mm和14.52 kN。相比工况1,工况8的动位移增大了17.5%,动索力减小了45%。对于工况5和工况12以及工况2和工况9也具有相同的规律(见表3)。主要原因为悬索的α相同,动力特征系数αb2越大,则初始垂跨比b较大,具有更强的变形能力。在相同的支座激励作用下,αb2较大的悬索变形更大,从而使得索力更小。对于αb2较小的悬索,端部激励对动索力的影响更大。

(2)悬索动力特征系数αb2越小,弹簧减震装置对悬索的减震效果越好。例如,在12 mm激励幅值作用下,αb2为0.04的工况5相比于工况1的δD为44%,δF为43%。而αb2为0.17的工况12相比于工况8的δD仅为10%,δF为28%。工况2和工况9对比也有相同的规律(见表3)。

3.3 阻尼系数ν对悬索的位移和索力响应的影响

(1) 阻尼系数ν对动力特征系数αb2=0.04悬索响应的影响

选择工况2、工况3、工况4、工况5和工况7为分析对象,研究阻尼系数ν对动力特征系数αb2=0.04悬索响应的影响。在A=12 mm,f=0.5 Hz及A=5 mm,f=1 Hz的两组加载制度下,上述6种工况的位移和索力响应对比,如表4所示。

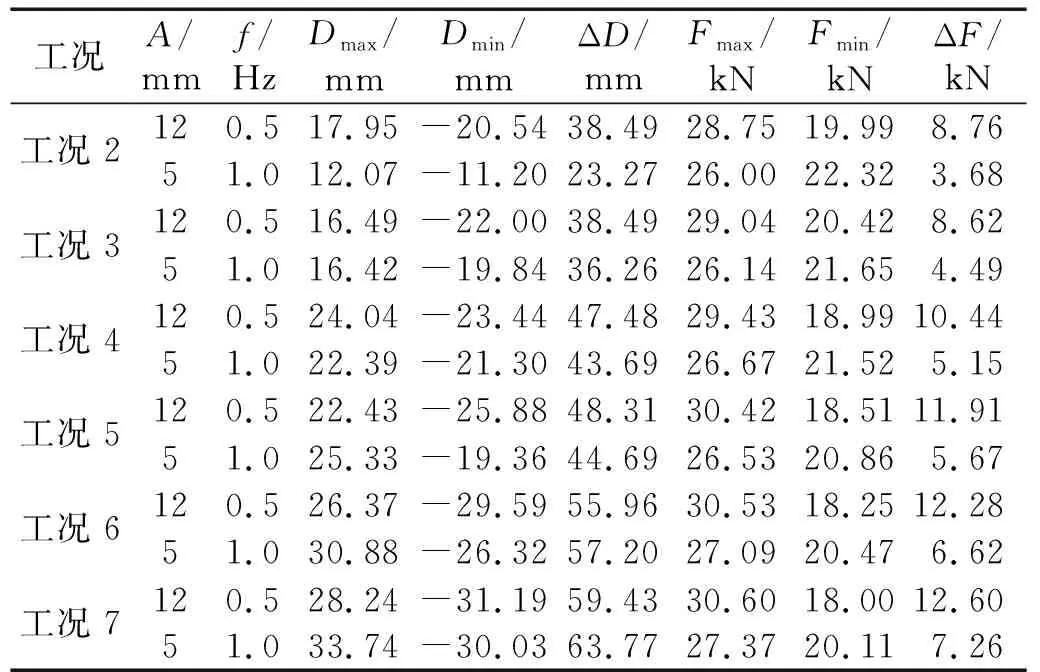
表4 附加阻尼对αb2=0.04悬索响应的影响Tab.4 The effect of additional damping on the cable response with αb2=0.04

由表4可知,在两种激励荷载作用下端部无黏滞阻尼工况(工况2和工况5)悬索的动位移和动索力均基本小于相应端部带黏滞阻尼工况(工况3、工况4、工况6和工况7),且对于端部阻尼系数更大的工况4和工况7(阻尼值均为105.6 kN(s/m)),其动位移和动索力要大于端部阻尼系数更小的工况3和工况6(阻尼值均为70.4 kN(s/m))。其主要原因为:一方面当悬索的初始垂跨比较小时,在悬索端部附加黏滞阻尼装置对悬索模态阻尼比的影响非常小(见表2,工况3、工况4、工况6和工况7的附加模态阻尼比分别为2.4%,2.9%,1.7%和2.1%),不能为悬索提供足够的附加阻尼比,减震效果不好;另外一方面,端部增加黏滞阻尼后,端部的约束刚度有所增加,因此造成了端部带弹簧和阻尼装置悬索的动位移和动索力比仅带弹簧装置悬索大,且附加阻尼越大,约束刚度越大,减震效果反而更差。通过以上分析,可以得到对于较小垂度的悬索,在端部仅设置弹簧装置减震即可,且弹簧刚度越小,悬索的减震性能也越好。

(2)阻尼系数ν对αb2=0.17悬索响应的影响规律

选择工况9、工况10、工况11、工况12、工况13、工况14分析阻尼系数对较大垂度悬索的响应影响规律。在A=12 mm,f=0.5 Hz及A=5 mm,f=1 Hz的两组加载制度下,上述6种工况的位移和索力响应对比,如表5所示。由表5可知,对于f=0.5 Hz低频加载,端部不带黏滞阻尼装置工况(工况9和工况12)的悬索动位移和动索力均接近相应的端部带黏滞阻尼工况(工况10、工况11、工况13和工况14),且端部阻尼值更大的工况(工况11和工况14)的动位移和动索力要大于端部阻尼值更小的工况(工况12和工况13),减震效果不明显。但是对于f=1.2 Hz高频加载,端部不带黏滞阻尼装置工况(工况9和工况12)的悬索动位移基本上要大于相应的端部带弹簧阻尼减震装置的工况(工况10、工况11、工况13和工况14),但是减震工况的动索力减震效果不明显。其主要原因为:①端部阻尼对较大垂度悬索提供的附加阻尼效果明显,工况10、工况11、工况13和工况14对应的1阶模态阻尼比ξ1分别为7.5%,9.3%,5%和6.6%;②当激励频率较小时,端部阻尼对悬索响应的减震效果不明显,随着激励频率(f=1.2 Hz)逐渐增大,激励频率接近悬索自振频率,端部阻尼对悬索减震作用逐渐增加。

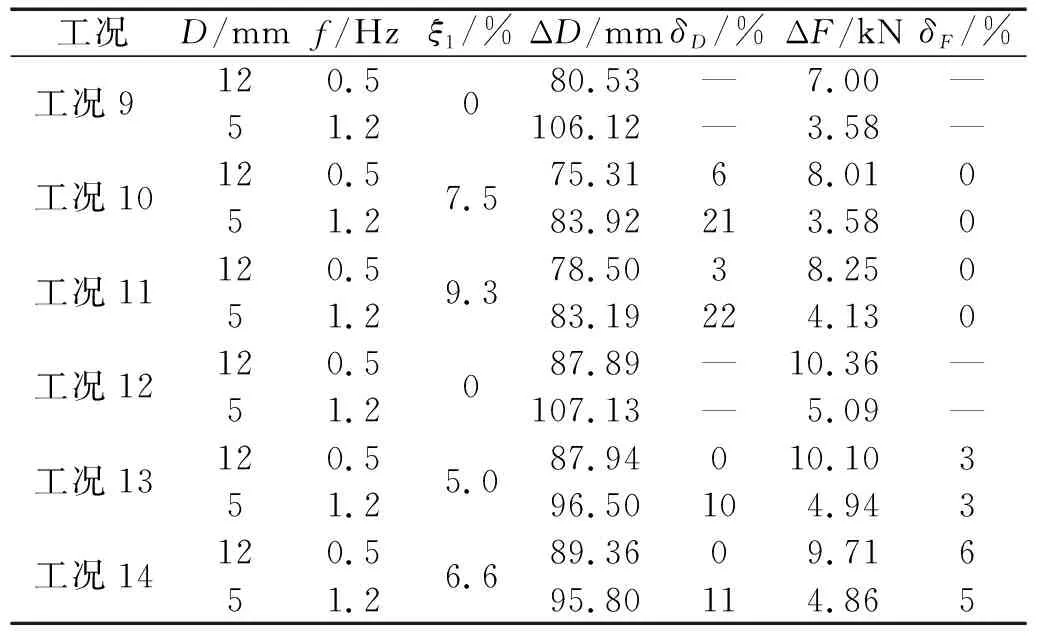
表5 附加阻尼对αb2=0.17悬索响应的影响Tab.5 The effect of additional damping on the cable response with αb2=0.17

为进一步研究悬索在近共振时的动力响应,对以上6种较大垂度的悬索工况进行了1.5 Hz激励频率的加载试验,该频率基本上达到了悬索的自振频率,悬索的位移和索力响应,如图14和图15所示。对于两个端部无黏滞阻尼工况(工况9和工况12),随着加载试验进行,悬索位移响应和索力响应的峰值均迅速增大,最大峰值响应不能收敛,最后出现了质量块旋转,悬索平面外扭转等现象,则终止了试验。工况9在试验终止前的动位移达到300.8 mm,动索力为14.3 kN;工况12的动位移达到348.6 mm,动索力为23.1 kN。而对于端部带弹簧-黏滞阻尼装置的工况(工况10、工况11、工况13和工况14),随着加载进行,位移和索力的峰值响应逐渐收敛,端部阻尼有效地控制了悬索的位移和索力响应。其中,工况10的动位移为119.3 mm,动索力为6.42 kN。与工况9相比分别降低了60%和55%。工况13的动位移为183.5 mm,动索力为13.9 kN,与工况12对比,分别降低了47%和40%。随着端部阻尼的进一步增加,悬索的位移响应进一步降低,但是索力响应降低不明显,其中,工况11的动位移和动索力分别为108.9 mm和6.2 kN,与工况10相比,分别降低了9%和0.3%。工况14的动位移和动索力响应分别为171.5 mm和13.9 kN,与工况13对比,降低了7%和0。可以看出端部阻尼增大后,悬索的附加模态阻尼比增大,悬索的动位移减小了8%左右而动索力降低较少。因此,当悬索在近共振时,端部仅带弹簧装置的悬索会出现振动不收敛现象,而端部阻尼可以有效抑制过大的振动变形,减震效果明显。

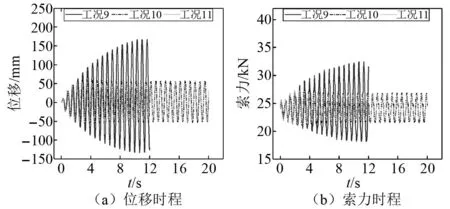
图14 端部带K1弹簧、αb2=0.04的悬索响应曲线Fig.14 Responses of the cable with spring K1 and αb2=0.04

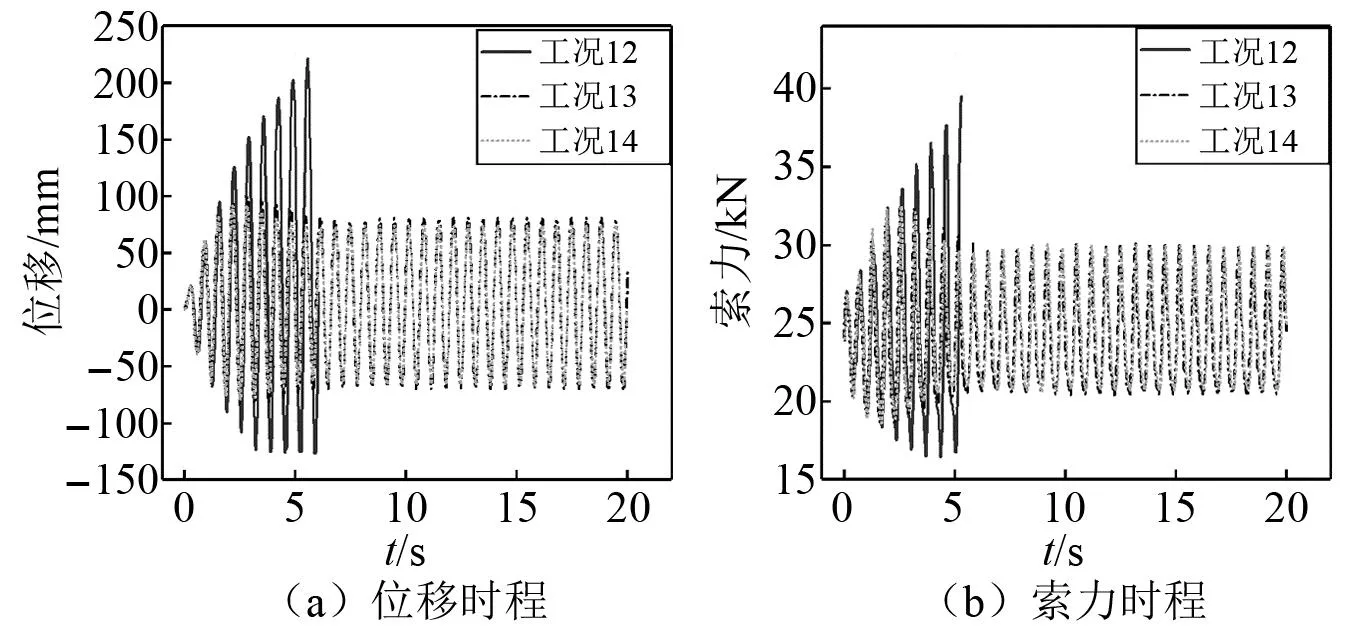
图15 端部带K2弹簧、αb2=0.04的悬索响应曲线Fig.15 Responses of the cable with spring K2 and αb2=0.04

4 结 论

针对相邻主结构间单向索采光顶的抗震问题,提出悬索端部附加减震装置的减震措施,通过理论分析及试验研究了减震体系的动力特性和动力响应,主要得到以下结论:

(1) 推导了端部带减震装置悬索结构频率和模态阻尼的无量纲计算公式,并通过自由振动试验检验了公式的正确性,研究表明悬索的振动特性由悬索动力特征系数αb2、刚度系数γk以及阻尼系数ν3个无量纲关键参数起控制作用。

(2) 基于理论公式研究了3个无量纲参数对体系频率和模态阻尼比的影响规律,分析了体系的阻尼特性。随着ν的增大,体系的模态阻尼比先增大后减小,存在一个ν值使得体系的模态阻尼比达到最大值。体系的模态阻尼比随着αb2的增大而增大,随着γk的增大而减小。针对αb2<0.34的小垂度悬索,建议了无量纲参数ν和γk的取值范围为:0≤ν≤150;0.2≤γk≤1.0,可为该类结构的工程设计提供参考。

(3) 进行了支座激励下端部带减震装置悬索体系的动力试验研究,研究激励频率和3个关键参数对悬索动位移和动索力的影响。结果表明,通过合理的设置减震装置参数,悬索的动索力和动位移可以减小30%以上。

(4) 当激励频率远离体系的自振频率或αb2较小时,减震装置的弹簧可以有效降低支座激励下悬索的动位移和动索力,且γk越小,装置的减震效果越好,减震装置的阻尼作用不明显。当激励频率接近体系的自振频率时,悬索端部仅附加弹簧减震装置发生了不稳定振动现象,而端部附加弹簧阻尼减震装置可以有效控制悬索的振动。因此,对于悬索的αb2较小或激励频率远离悬索自振频率,可仅在悬索端仅设置弹簧减震装置;对于激励频率接近悬索自振频率且悬索的αb2较大时,可在端部设置弹簧阻尼减震装置。