基于ANSYS Workbench下盐河尾水南地涵结构响应特征及疲劳特性研究

宋焰龙，赵泽月，潘 辉

(1.江苏省灌溉动力管理一处，江苏 泰州 225300；2.江苏省泰州引江河管理处，江苏 泰州 225300)

水工建筑的安全可靠性与荷载类型、作用时间以及运营特点密切相关，考虑水利结构的动力响应变化，则是应对变荷载、往复荷载的工况。地涵工程运营时，常受上部交通循环荷载影响，从而改变结构运营效率，乃至结构寿命[1-2]。杜为彬[3]、赵天玉[4]为研究地涵结构设计特征，考虑水工设施所处工程环境，开展了结构应力、位移特征研究，从宏观设计分析涵洞结构的最不利工况，探讨地涵结构的最优设计方案。熊磊等[5]、曹睿哲[6]为研究水闸等水利-交通多用途设施，考虑动荷载变化特点，采用仿真计算方法对闸室开展了动力响应计算，分析闸体结构自身加速度、位移响应变化，为工程加固、除险提供依据。陈敏等[7]、吴小龙[8]为研究涵洞、水闸等结构在往复荷载下振动变化，并耦合流固耦合场等实际问题，分析了交通往复荷载下涵洞等结构模型的应力、位移变化，并提出了变荷载与涵洞运营疲劳寿命之间关系，为工程运营提供参考。本文为研究盐河尾水南地涵工程受上部交通荷载影响特性，分析了往复荷载作用距离、闸门开度两因素与之关联性，并探讨了涵洞运营疲劳寿命影响变化，针对工程设计提供了相应建议。

1 研究方法

1.1 工程概况

盐河尾水南地涵工程乃是灌云县境内新沂河、盐河以及岑池河交汇区重要水利控制枢纽，对调节上游尾水交汇、新沂河入海以及岑池河泄洪均具有重要水利价值。该地涵洞顶高程为10.6m，上方有供通行交通桥，宽度为4m，采用独立式抗震构件与洞顶下方承压板搭接，确保上方交通桥面具有独立抗震验算构件，交通桥高度为6.4m。涵首设置有平面钢闸门，高度可达4.2m，匹配有16t级启闭机，工作时启闭机振动引起的自振位移不超过2.5mm，即使在满开度工况下，启闭机运营不会造成地涵结构底板或洞口上方交通桥发生较大自振变化，故可不考虑启闭机引起的自振响应特性。作为区域内多条地表干流的重要水利控制设施，在盐河尾水地涵工程运营期，进行了全周期全寿命的智慧水利监测分析，结构剖面监测点分布示意如图1所示，获得了上部交通桥、闸室底板以及洞墩的结构位移、渗流特征，数据表明，该地涵工程存在较显著危害的为上部交通桥的反复荷载间歇性变化，在时速为60、80km/h行车荷载下，地涵结构各测点均能获得X、Y、Z向加速度响应特征，3#、7#测点所获得X向峰值加速度可达0.08m/s2，不论是通过功率谱或傅里叶变换分析，监测数据均表明，该地涵工程上方交通桥的循环荷载，很容易导致闸洞内发生明显振动响应，结构变化以及疲劳寿命随之会有影响变化。为此，地涵管理部门考虑开展对上部交通往复荷载引起的地涵结构响应特征影响进行仿真分析。

图1 结构剖面监测点分布示意

1.2 建模方法

为准确分析上部往复荷载对下部地涵闸洞结构影响，引入流固耦合仿真计算方法，对闸室结构动力响应水平开展分析。在流固耦合场内，流体运动方程满足下式：

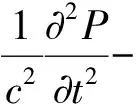
(1)

式中，c—介质中声速，m/s；P—声压，Pa；t—时间，s。

依据有限元插分求解方法，离散化上式，获得下列向量表达式：

(2)

对式(1)的运动微分方程离散化表达，获得下式：

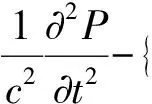
(3)

基于地涵闸洞内流体分布域，考虑边界条件存在，获得积分解：

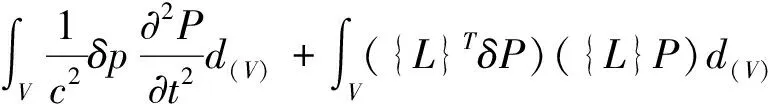
(4)

式中，V—流体分布域，无量纲；δp—压力增减量，Pa；s—体积模量，Pa；{n}—接触面法向量，无量纲；{L}—Laplace算子，无量纲。

由于流固耦合场内不仅存在流体运动控制方程，同样还有固体运动解，因而借助流、固接触面质点运动方程表达式，获得下式：

(5)

式中，{W}—接触面位移矢量方向。

可采用向量表达式，即上式为：

(6)

联立(4)(6)式后，可得到：

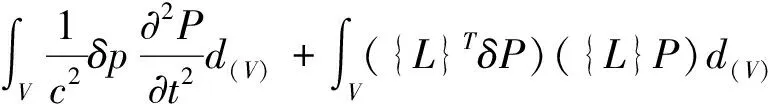
(7)

在地涵闸洞内，受限于上部往复荷载的动力影响，其渗流场、运动场均会发生变化，以运动位移U以及水头压力P为分析参数，得到下式：

(8)

式中，{N}、{N′}—压力、位移的形函数，Pa、m；{Pe}、{Ue}—压力、位移的矢量式，无量纲。

在流固耦合场内，流固相互作用下仍满足能量守恒，并假定耗散能仅存在于流固场交界面，联立(7)(8)式可得到：

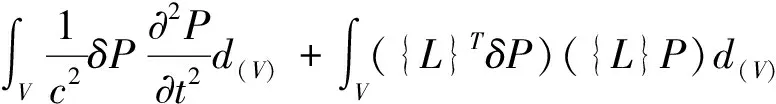
(9)

式中，r—边界处阻抗系数，无量纲。

切换为向量表达后，上式为：

(10)

综合上述运动方程，可得到流固耦合场质点作用表达式[9-10]：

(11)

式中，ρ0—密度；[Re]—边界阻抗系数矩阵；N′、N—与工程结构相关的参数矩阵；以上参数均无量纲。

基于上述流固耦合理论分析，借助ANSYS仿真计算平台开展建模计算[11]，该地涵工程简化部分附属建筑后，所建立的交通桥-地涵联合模型如图2所示，模型影响域内的顺水流方向宽度为8m，垂直水流向长度为12m，涵洞结构高度按照4.5m设定，所在场地影响范围土层深度为15m，依次从第四系沉积土至粉质砂土层。结合盐河尾水南地涵工程实际用材，采用四面体单元为网格体，具有三维10节点的自由度，计算参数按照工程实际用料设定。模型的X、Y、Z正向分别取顺水流、涵洞闸门开启向以及竖直上方向。基于上述参数设定，对计算模型进行网格划分如图3所示，获得了有限元仿真模型，地涵结构整体与独立模型如图4所示，共获得了单元数达126432个，节点数168527个，网格精度及质量均满足计算收敛条件。

图2 交通桥-地涵联合模型

图3 地涵结构整体与独立模型

图4 人工粘弹性边界条件模型

考虑人工边界影响，采用人工粘弹性修正边界，相应的边界法、切向系数分别设定为1.35、0.65，施加边界条件后模型如图4所示。计算荷载包括了上部交通往复荷载以及自身结构自重，第一部分往复荷载为本文研究重点，后部分结构自重直接按照静荷载考虑；由于往复荷载受多因素影响，如荷载作用点以及涵洞启闭状态等，均会影响往复动荷载对结构计算结果。因而，本文研究对象设定有往复荷载的作用距离L以及涵洞闸门开度α，分别探讨两因素下涵洞结构动力响应水平。

2 地涵结构响应特征分析

为研究地涵结构在交通往复荷载作用下响应特征差异，分别设定了往复荷载的作用距离L与涵洞闸门开度α研究组，其中前者距离组分别有0、10、20、30、40、50、60、70、80、90m共10组，此距离指荷载作用点与交通桥面中心点间距；后者闸门开度α组分别设定开度0、0.1、0.2、0.4、0.6、0.8、1，开度α以多孔闸门全部开启时为1进行换算[12]。

2.1 往复荷载作用距离

基于交通往复荷载不同作用距离方案下仿真计算，获得了往复荷载作用距离与涵洞结构等效应力、位移响应关系，如图5所示。分析图5(a)可知，总体上往复荷载作用距离愈远离桥面中心，则等效应力愈低，尤以作用距离L为60m后，等效应力响应值实质上处于较低水平，稳定在0.009MPa。在往复荷载作用距离L为0～50m时，等效应力随作用距离依次递减，但降幅逐步减弱，如作用距离0～30m时，等效应力分布为0.14～0.019MPa，降幅依次为63.7%、41.9%、32.8%，而在作用距离40、50m时，降幅分别为26.4%、15.7%，甚至在作用距离80～90m时，等效应力响应值降幅仅为5%左右。由此可知，往复荷载作用距离对涵洞结构影响为逐步减弱，荷载作用距离安全区间应在60m内。

图5 作用距离对结构响应特征影响

从图5(b)可看出，在荷载不同作用距离下，涵洞结构高度方向上位移响应变化趋势各有不同，在作用距离L为0～40m时，位移响应变化以结构高度3m为分界点，在结构高度3～4.5m上，结构位移响应具有更显著增幅，实质上该区间内位移响应值早已超过涵洞允许值。不同的是，在作用距离为60、80m时，位移响应增长较稳定，且增幅弱于前者方案，如作用距离80m方案下，涵洞结构位移响应分布为0.084～0.174mm，结构高度方向上位移平均增幅仅为5.4%。由此可知，往复荷载作用距离差异性，会导致结构高度方向上结构响应幅度以及趋势变化的不同。

2.2 涵洞闸门开度

同样的，从计算结果中提取获得了不同开度方案下涵洞模型的动力响应变化，如图6所示。由图6(a)中等效应力变化可知，当闸门开度增大，等效应力均为递增，尤以闸门开度0.4后，应力增幅最显著。在闸门开度0～0.4时，等效应力分布于0.015～0.018MPa，平均增幅仅为5.8%，而闸门开度0.6～1下，等效应力增幅一级比一级高。不难看出，当闸门开度增大，实质上涵洞内流固耦合场作用效应更强，动、静水压力的变换，对涵洞模型等效应力有一定叠加作用影响。

图6 闸门开度对结构响应特征影响

分析图6(b)可知，不论闸门开度α如何变化，涵洞高度方向上位移响应变化趋势并不会发生较明显差异，均较稳定递增，洞顶位移始终高于洞底。另一方面，闸门开度α递增或递减，结构位移响应值差异也较小，如闸门开度α为0、0.2时，位移响应值分布为0.139～0.182、0.149～0.196mm，在高度方向上位移平均增幅分别为1.9%、2.3%，而闸门开度为0.4、0.8时，位移值较前两者增长并不显著，平均增幅甚至基本接近，为2.4%、2.3%。分析表明，闸门开度α变化，涵洞高度方向上位移响应值差异性较小，位移增幅以及位移值均受之影响较弱，主要影响仍在于应力水平。

3 地涵结构疲劳特性分析

在交通往复荷载作用下，实质上涵洞结构运营寿命会有一定影响，分析地涵结构疲劳特性有其工程意义，在ANSYS Workbench中，通过自定义线性结构材料因子，考虑载荷作用距离以及闸门开度因素影响，获得了涵洞结构疲劳寿命，并以循环次数N作为寿命衡量指标，如图7所示。

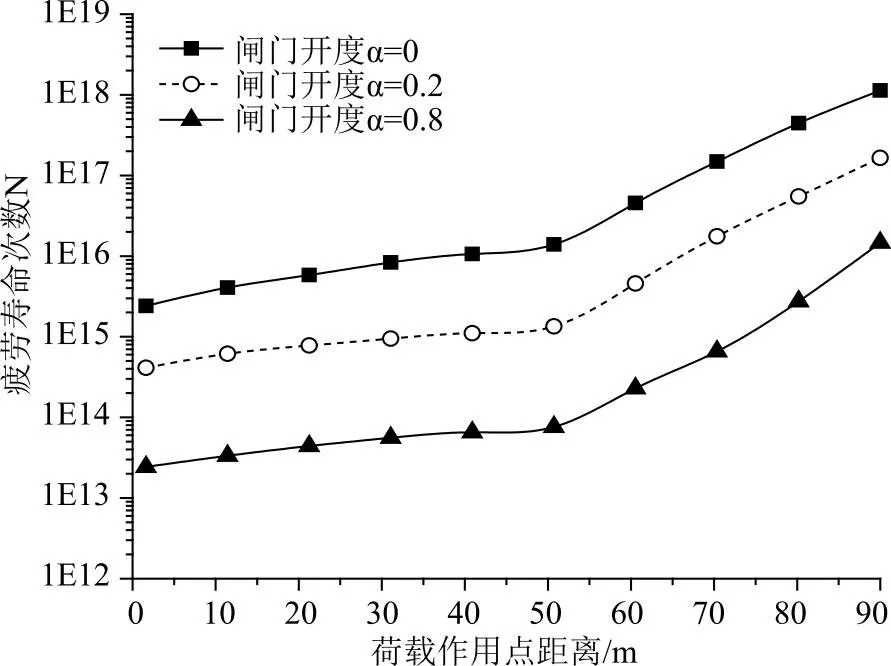
图7 涵洞结构疲劳寿命影响变化

由图7中疲劳寿命N变换过程可知，荷载作用距离与疲劳寿命为正相关特征，尤以疲劳寿命60m后，疲劳寿命随之增长更明显，在闸门开度α为0.2时，作用距离0～50m时，疲劳寿命N分布于4.18×1014～1.37×1015，平均增幅为27.3%，而在作用距离60～90m时，疲劳寿命平均增幅可达2.35倍，分布于4.66×1015～1.69×1017。当闸门开度增大，疲劳寿命与荷载作用距离关联性并未发生变化，且整体上疲劳寿命N变幅基本较为接近其他开度方案。当闸门开度增大，涵洞结构疲劳寿命N均为递减，如开度α为0时，荷载作用距离40m下疲劳寿命为1.08×1016，而同作用距离下的开度α为0.2、0.8方案下疲劳寿命较前者分别减少了89.6%、99.4%。由此分析，闸门开度会改变涵洞结构运营疲劳寿命，但影响效应弱于荷载作用距离因素；从工程设计考量，应着重于涵洞上方交通往复荷载的控制，闸门开度保持在合理、规范运营即可。

4 结语

(1)荷载作用距离愈大，则涵洞结构应力响应愈低；荷载作用距离会影响涵洞高度方向上位移响应变化，尤以作用距离60m后，位移响应增幅减弱且趋于稳定。

(2)闸门开度增大，等效应力递增，开度0.4后增幅最显著；闸门开度变化，不会改变涵洞结构位移响应变化趋势，对位移响应值影响也较低，各方案下位移响应值增幅接近，为2%左右。

(3)研究得到荷载作用距离与涵洞疲劳寿命参数N为正相关关系；同时，闸门开度增大，疲劳寿命N递减，整体递减效应较弱，影响幅度不及往复荷载作用距离因素。