最优化岩石爆破的理论及方法探索

董少南，高 烈，李向明，张敢生

(1.本钢技术中心，辽宁 本溪 117000；2.辽宁安达爆破工程有限公司，辽宁 本溪 117000；3.中国矿产资源集团有限公司，河北 雄安 071799；4.本钢歪头山铁矿，辽宁 本溪 117005；5.辽宁科技学院，辽宁 本溪 117004)

0 引言

在岩石爆破中，追求综合爆破危害效应最小、综合破碎效果最佳称之为最优化爆破。最优化问题是岩石爆破领域最难解决的难题，现有理论还不能完全给予科学合理的解答。由于现有理论的局限性导致在工程实践中许多情况下不知应当如何处理，造成质量事故及安全事故频繁发生。因此，最优化爆破是岩石爆破领域最亟需解决的重要问题。

1 岩石爆破最优化方法的选择

在探索初期试图应用现代系统工程论中的最优化方法来解决问题，但经过多年研究后发现这种方法对于解决岩石爆破的最优化问题无能为力。

笔者转向对岩石爆破系统各个阶段的运行规律进行研究。在这种思想指引下并经过长期的爆破实践，发现了岩石爆破各个阶段的基本规律。它们是爆区岩石最佳破碎原理、最优炸药单耗原理、能量平衡分配原理、可碎能带分布原理、单孔爆破最佳破碎原理及面能比中值化原理，分别对这几个基本原理的内容、提出的原因和依据、能够解决的问题进行阐述。

2 最优化岩石爆破理论的基本内容

2.1 爆区岩石最佳破碎原理

2.1.1 提出的原因和依据

原因：解决爆破的最优化问题，首先必须解决如何布孔、如何起爆，才能使整个爆区的岩石处于最佳破碎状态问题，为此提出爆区岩石最佳破碎原理。

依据：一是在探求布孔参数与爆破效果关系时发现，虽然最小抵抗线、孔网参数、布孔方式、药包直径和岩石赋存条件等都是与爆破效果相关的影响因素，但是如果其它参数不变，单独改善某一个参数都不能改善总体爆破效果。因此，这些参数都不是在布孔方面决定爆破效果好坏的根本因素，一定存在一个与这些参数相关而决定爆破效果好坏的根本因素，这个因素就是爆炸能量的分布均匀度，标定爆炸能量分布均匀度的参数就是标准爆能体的空间利用率。二是在探求起爆参数与爆破效果关系时发现，与前述布孔参数类似，也一定存在一个与这些参数相关并决定爆破效果好坏的根本因素，这个因素就是相邻起爆炮孔的综合能量梯度。

2.1.2 内容

根据爆破实践，得出整个爆区的岩石最佳破碎原理：在炸药和岩石一定的条件下，以综合效果为最优的岩石爆破中，爆区的岩石破碎效果与整个爆区的炸药能量分配均匀度、相邻起爆炮孔的综合能量梯度成正相关。因此，要实现最优化爆破必须使炸药能量分配均匀度和相邻起爆炮孔的综合能量梯度值均达到最大化，这个原理就是爆区岩石最佳破碎原理。

1)能量分配均匀度的概念及计算。能量分配均匀度是指爆炸能量在整个爆区岩石中分布的均匀程度。

爆能体与标准爆能体的概念。爆能体是爆炸能量在岩石中各个方向传播的能量波波阵面所构成的空间结构体。标准爆能体是在标准布孔方式下，两个相邻且同时起爆的药包相切时的爆能体。

绝对均匀度的计算：

(1)

式中：J—爆炸能量分布的绝对均匀度；V标准—爆区内所有药包的标准爆能体所占据的空间体积；V曲面空间—爆区内与最外侧标准爆能体相切的曲面空间所围成的空间体积。

2)能量梯度的定义及计算。能量梯度是指爆炸能量密度在单位距离上的变化量。

能量梯度的计算：

(2)

式中：G—能量梯度；△e—两相邻炮孔在同一瞬间能量密度的差值，可根据能量密度变化曲线方程进行计算；L—炮孔间距。

3)爆炸能量密度的变化曲线。从微观上看，每个药包的爆破过程都是一个由压应力为主向拉应力为主的转换过程。这个过程可用能量密度变化曲线方程表示，经验公式如下：

(3)

式中：e—能量密度；u—爆炸能量综合效应的传播速度；Pr—岩石中冲击波峰值压力；T—岩石破碎时间；t—爆破过程各瞬间；x—爆区各点距离药包中心距离；k—修正系数。

4)解决的问题。根据爆区岩石最佳破碎原理可解决布孔方式和起爆顺序的最优化设计问题。

2.2 最优炸药单耗原理

2.2.1 提出原因和依据

原因：解决岩石爆破的最优化问题，必须解决的第二个问题是爆区的最优炸药量计算问题，为此提出最优炸药单耗原理。

依据：当前最优炸药量的计算主要是根据利文斯顿爆破漏斗理论，但是结果与实际用量存在一些差距。分析造成这个差距的原因不是最优爆破漏斗理论存在错误，而是把单药包的爆破漏斗理论应用到多药包的爆区存在系统误差。原因是在单药包爆破漏斗实验中已被利用但没显现出来的爆炸能量，在多药包的爆区中就会显现出来。因此为了解决爆区最优炸药量的计算问题，提出了最优炸药单耗原理。

2.2.2 内容

通过实践得知每个炮孔的有用能量利用率随着炸药量和周围抵抗线的变化而变化，只有当每个炮孔的有用能量利用率达到最大时，爆区的炸药单耗才能达到最优，而炮孔的有用能量利用率达到最大化的条件是爆炸能量在自由面法线方向和水平方向有用能量的分量乘积达到最大，即在一个水平自由面的情况下爆破作用指数n=0.5时炸药单耗最优。这个结论可从理论和实践两个方面得到证明。

2.2.3 解决的问题

能够解决爆区及每个炮孔最优炸药量的计算问题。

2.3 能量平衡分配原理

2.3.1 提出的原因和依据

原因：解决岩石爆破的最优化问题，必须解决的第三个问题是爆炸能量在各个方向的计算问题，为此提出能量平衡分配原理。

依据：多自由面硐室爆破实践表明，爆炸能量在岩石中各个方向的分配与此方向的岩石阻力存在一定规律，这个规律就是能量平衡分配原理。

2.3.2 内容

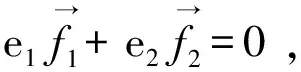
2.3.3 解决的问题

此原理可解决岩石爆破中随着自由面、岩石赋存条件及岩石应力的变化，导致炸药量发生变化的问题。

2.4 可碎能带分布原理

2.4.1 提出的原因和依据

原因：解决岩石爆破的最优化问题，必须解决的第四个问题是爆破漏斗区域内爆炸能量的径向分配问题，为此提出了可碎能带分布原理。因为这个问题不解决，就不知道何种状态有利于岩石破碎、何种状态不利于岩石破碎，因而也就不知道应当如何调整装药结构以改善爆破效果。

依据：一是根据岩石的开裂速度与岩石的破碎时间，可确定从自由面到爆源间的岩石开裂点是多点，而不是一点。二是根据距离爆源相同距离区域的岩块大小存在近似相同现象，推断距离爆源相同距离的一定范围内具有大致相同的能量密度。三是根据距离爆源越近的区域岩块越小，距离爆源越远的区域岩块越大现象，推断距离爆源越近的地方能量密度越高、距离爆源越远的地方能量密度越低。四是根据距离自由面不同距离的各级岩块几何尺寸大小具有近似等比关系现象，推断能量密度从爆源到自由面依次呈等比级数降低的关系。五是根据爆破漏斗半径与炸药量关系曲线存在突变现象，断定由岩石与炸药组成的系统整体(而非局部)存在一个状态转折点。当系统药量达到转折点处药量时，系统岩石处于可碎状态；当系统药量达不到转折点处药量时，系统岩石处于不可碎状态，而这个状态转折点就是岩石形成可碎能带体系的重要标志。

2.4.2 内容

可碎能带分布原理的内容：在爆破漏斗区域内岩石破碎的首要条件是必须形成可碎能带体系，且体系能量呈现如下分布特征：①爆炸能量从爆源到自由面呈现不同能量密度的多级条带分布。②每个条带能量密度值都大致相同，且数值大于岩石破碎所需的最小能量密度值。③能量密度从爆源到自由面依次呈等比级数降低的关系。④爆炸能量在爆破漏斗区域内具有量子化分布特点，能带级数只能在大于1的正整数范围内取值。

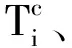
2.4.3 单孔爆破岩石最佳破碎原理的内容

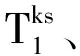
2.4.4 解决的问题

应用可碎能带分布原理和单孔爆破最佳破碎原理可解决单孔爆破最优装药结构的问题，并依此提出主辅药包法是在安全前提下最有利于岩石破碎的一种装药方法。

2.5 面能比中值化原理

2.5.1 提出的原因和依据

原因：在岩石爆破过程中，为什么会产生不同的岩块形状和数量？是什么因素在控制岩石的破碎形状和数量？为了解决以上问题，提出了面能比中值化原理。

依据：一是爆破岩块之间形状存在相似性。这种现象表明有某种因素在控制岩石的破碎形状，这种作用因素就是面能比最小化原理。二是在爆破漏斗内岩石是多级多块度破碎而不是单级单块度破碎，这种现象表明有某种因素在控制岩石的破碎数量，这种作用因素就是面能比最大化原理。

2.5.2 面能比中值化原理的内容

所谓面能比中值化原理就是在由岩石和炸药组成的系统中，为了同时满足两个对立统一的相互作用而趋于平衡的一种破岩原理，这两个对立统一的相互作用就是使爆炸能量获得最大释放的面能比最小化原理和捕获更多爆炸能量的面能比最大化原理，在这两个原理的共同作用下使特定的岩石爆破系统的面能比趋于特定的常数。

从功能来讲，面能比最小化原理对岩块形状起主要作用而对岩块数量起辅助作用，同时面能比最大化原理对岩块数量起主要作用而对岩块形状起辅助作用。

2.5.3 解决的问题

解决了岩石破碎成块的机理问题，应用此原理并结合二次破碎及岩石弱面的数理模型可以精确预测爆堆岩块形状和数量。

3 方法简述

根据上述原理，提出实现最优化岩石爆破的方法：①根据爆炸能量分布均匀度最大化原则布置炮孔。②根据相邻炮孔的综合能量梯度最大化原则安排起爆网络。③根据主辅药包法原则设置装药结构和填塞方法。④根据面能比中值化原理、岩块二次碰撞破碎数理模型及岩体结构弱面数理模型预测爆堆岩块形状和数量。

4 结语

文中提出的每条原理都是多年爆破实践经验的总结和严谨逻辑推理的结果。比如爆区布孔原理的提出就是在长期的实践中发现现有的“大孔距小抵抗线布孔原理”存在以下不足：一是不知炮孔临近系数m值为何时布孔最优。二是无法解释在相同m值不同布孔方式下，爆破效果不同的现象。三是无法解决随着岩石赋存条件的变化，布孔参数和方式应当如何变化问题。由此必须引入新参数，这个参数必须具有以下功能：一是这个参数必须是客观存在的，二是这个参数的变化必须能够同时兼顾炸药和岩石的变化。三是这个参数必须与爆破效果成正相关。因为只有满足这三个功能才能把各种不同布孔的爆区区别开来，也才能知道哪个更好，否则何谈最优。通过对所有爆破参数进行现场考察，发现只有能量分布均匀度具备上述功能，而且只有根据标准爆能体的空间利用率进行计算才更合理，故此提出根据能量分布均匀度进行布孔的原理。其它几个原理的提出亦是如此，都是客观现实的需要，并非为了创新提出的新概念。由于篇幅限制，无法把每个细节进行展开，只能予以概述。

在提出这套理论和方法后，又经过500余个复杂环境下岩石爆区的检验，证明采用这种方法爆破的爆区均能获得较好的爆破效果，所以这套理论和方法是能够经受住实践检验的。客观来说这套理论和方法还有一些不足，主要表现为以下方面：一是由于存在大量复杂的数学计算，不实现计算机程序化难以推广应用。二是由于引入一些新参数，而参数的现场测定技术还需要解决。三是结论更多源于实践经验而缺乏精密的实验验证。四是由于研究的水平和条件限制，暂时还解决不了所有存在的问题。