弱电网下LCL型并网逆变器的改进稳定性控制方法

石锋杰，马 雁，许 多，辛业春

(1.郑州电力高等专科学校 电力工程学院，河南 郑州 450000；2.东北电力大学 电力工程学院，吉林 吉林132012）

0 引言

光伏并网逆变器在光伏发电系统中承担着能源转换的重要作用，一方面光伏并网逆变器需要将光伏板所产生的直流电经过Boost电路升压后转换成交流电汇入电网，另一方面光伏并网逆变器需要维持交流电的电能质量，减小对电网的污染[1]，[2]。然而，随着光伏发电系统或其他新能源分布式发电系统的大量并网，电网电压的电能质量呈现弱电网形式，主要表现为电网阻抗以及并网点电压出现谐波[3]，其中，前者会使并网逆变器谐振点发生偏移，后者会对电网电压前馈的控制回路产生影响。

弱电网下，电容电流反馈有源阻尼法是应对LCL滤波器谐振效应的有效方法，通过在滤波器电容上并联虚拟电阻，避免了无源阻尼法的功率消耗[4]。文献[5]在此基础上提出了外环全局鲁棒滑模控制和内环电容电流的比例-惯性反馈控制，但是未考虑弱电网下电网阻抗的影响。文献[6]为提高电容电流反馈法的有效阻尼区，提出了将相位超前补偿环节加入电容电流反馈支路，提高了电网阻抗变化时的系统稳定性。但是相位超前补偿环节引入了较多的补偿参数，参数设计增加了控制复杂度。电网电压前馈法也是应对谐振的有效手段，但额外引入正反馈回路会降低相角裕度[7]，[8]。文献[9]提出采用多谐振电网电压前馈结合相位补偿器以提升系统的稳定性和相位裕度，但未提及电容电流反馈系数的选取方法。

本文针对弱电网下的并网逆变器控制特性，分别采用修改电容电流反馈系数和多谐振电网电压前馈的方式应对电网阻抗和电网电压谐波。根据电网阻抗值修正电容电流反馈系数，提出了一种查表法参数选取方法以满足电网阻抗变化时的稳定性要求，利用准比例谐振控制器的多谐波控制性能应对并网点电压谐波。

1 弱电网下并网逆变器模型

图1为弱电网下并网逆变器的结构图。本文以T型三电平逆变器作为并网逆变器，图中：Lxwg和Rxwg组成了弱电网阻抗；ex为理想电网电压；逆变器侧电感Lxi、电容Cx以及电网侧电感Lxg组成了交流侧LCL滤波器；Udc为直流侧电压；uC1和uC2分 别 为 直 流 侧 上、下 电 容 的 电 压；x=a，b，c。

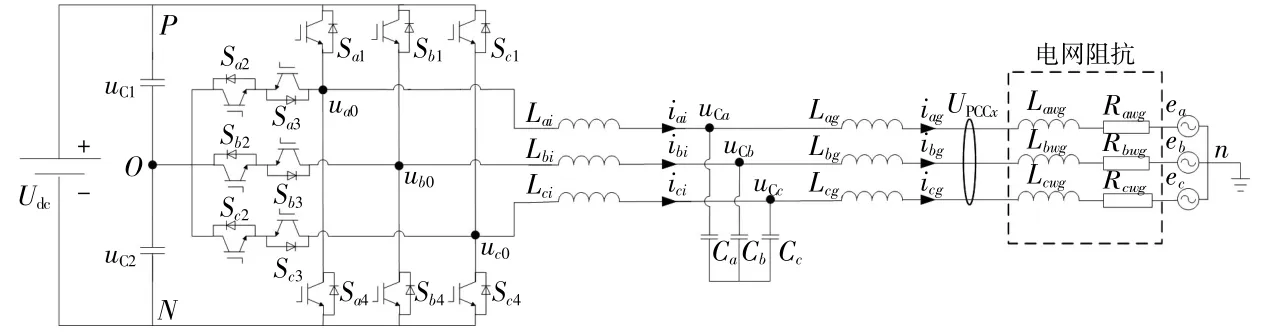
图1 弱电网下并网逆变器结构图Fig.1 Structure diagram of grid-connected inverter under weak grid

LCL型并网逆变器谐振问题的解决方法一般分为无源阻尼法和有源阻尼法。无源阻尼法通过在LCL滤波器的滤波元件上串联或者并联电阻以实现阻尼的效果，显然无源阻尼法会对系统产生损耗，因此无源阻尼法通常不被单独使用。有源阻尼法通过增加虚拟电阻模拟6种无源阻尼法(图2），在6种无源阻尼法中，电容并联电阻法可以抑制谐振峰，保证低频和高频段的增益效果。

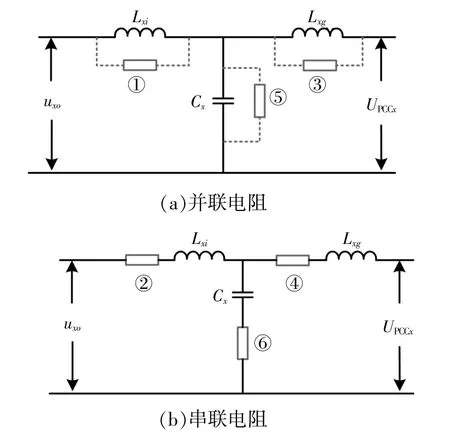
图2 6种无源阻尼法Fig.2 Six passive damping methods

2 考虑电网阻抗的谐振抑制方法

图3为弱电网下考虑电网阻抗的s域单相电流控制框图。其中：并网电流采用比例谐振控制，电容电流反馈用于抑制谐振，反馈系数为H1，并网电流反馈系数H2=1；GQPR为并网电流控制器传递函数；Ginv为逆变器的传递函数；Gvol为并网点电压前馈控制器传递函数。

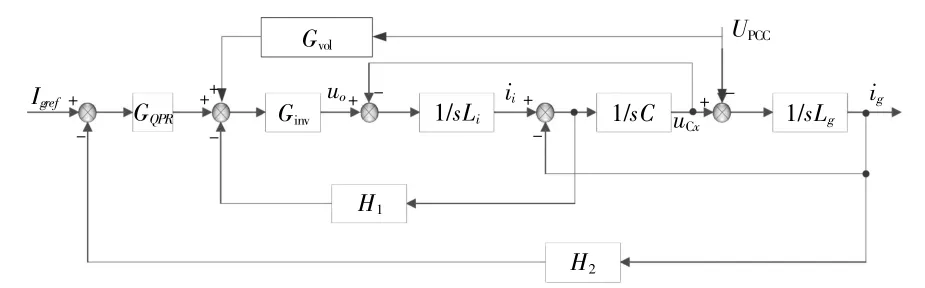
图3 考虑电网阻抗的s域单相电流控制框图Fig.3 Block diagram of s-domain single-phase current control considering grid impedance

为了方便表示，图中的参数均去除了相位信息x，Lg不仅包含电网侧电感Lxg，也包含了电网电感Lxwg，本文不考虑相当于阻尼作用的电网阻抗的阻性成分。

根据图3得到开环传递函数的表达式为

式中：Li为逆变器侧电感；C为滤波器电容；s为s域平面中的复数变量。

根据式(1），能够绘制出在固定的电容电流反馈系数下电网阻抗变化时的系统Bode图，如图4所示。当不考虑电网阻抗时，设计合适的控制参数能够使系统处于稳定状态；当考虑电网阻抗且采用固定的电容电流反馈系数时，随着电网阻抗的提高，LCL型并网逆变器系统的谐振峰向左偏移，且在相位裕度穿越-180°时幅值裕度随着电网阻抗的提高而升高，在幅值裕度大于0时，系统会发生失稳现象。当采用固定的电容电流反馈系数抑制谐振时，电网正常情况下的参数可以满足谐振抑制效果；当弱电网下的电网阻抗不可忽略时，固定的参数难以满足变化的电网阻抗带来的稳定性影响。因此，通过改变电容电流反馈系数应对弱电网下的电网阻抗变化是非常有必要的。

图4 考虑电网阻抗时的Bode图Fig.4 Bode diagram considering grid impedance

图5为电网阻抗为1 mH时，不同的电容电流反馈系数下系统的Bode图。从图中可以看出，当考虑电网阻抗时，较小的电容电流反馈系数不能满足系统稳定性要求。即在H1=0.05时，不考虑电网阻抗时系统不稳定。当升高H1时，如H1=0.07，由于控制参数的改变，Bode图的幅值裕度在相角裕度穿越-180°时系统得到稳定。继续升高H1至0.20，幅值裕度的峰值继续降低，增加了系统的稳定裕度。通过改变电容电流反馈系数的值能够应对变化的电网阻抗，证明了本文所述方法的有效性。当光伏并网逆变器系统设计完善，其硬件参数均固定时，只需要根据电网阻抗的值修改电容电流反馈系数的值即可保证系统稳定性。

图5 不同电容电流反馈系数对系统稳定性的影响Fig.5 Influence of different capacitive current feedback coefficients on system stability

本文在大量仿真及Bode图的汇总下，提出了一种查表法的电容电流反馈系数选取方法。当采用如表1所示的硬件参数时，可以得到电网阻抗与电容电流反馈系数之间的关系，如表2所示。其他硬件参数，也可以按照相同的方法进行选取。

表1 硬件参数Table 1 Hardware parameters

表2 电网阻抗与H1的关系Table 2 Relationship between grid impedance and H1

3 改进电网电压前馈方法

弱电网下，并网点电压存在的谐波将带来并网电流的发散，因此如何处理并网点电压谐波也相当重要。准比例谐振(Quasi Proportional Resonance，QPR）控制是一种针对交流信号的控制器，其特点是对特定基频倍数信号的控制效果较好。QPR控制器是来源于比例谐振(Proportional Resonance，PR）的 控 制 器，PR控 制器的传递函数为

式中：Kp为比例系数；Kr为谐振系数；ωo为被控信号的谐振角频率。

式(2）所述的PR控制器是一种理想的控制器，其在基频处的增益接近于无穷大，能够实现对基频信号的无静差跟踪。然而，实际中的PR控制器是比较难以实现的，因此，通常采用QPR控制器代替理想的PR控制器。QPR控制器的传递函数为

式中：ωc为截止频率。

为了抑制弱电网下并网点电压的谐波，本文采用多谐振控制器的准比例谐振控制器，使电压前馈通道在电网主要低次谐波频率处保持反馈特性，并对其余非基波频率处的频段进行有效抑制[9]。本文采用的多谐振控制器的传递函数为

式中：Kpu为电压前馈通道比例系数；n为谐波相对于基波频率的倍数。

图6为多谐振控制器传递函数的Bode图。从图中可以看出，当采用多谐振控制器时，在基波频率、3倍基波频率、5倍基波频率、7倍基波频率、9倍基波频率处的增益较大，证明了多谐振控制器能够对特定频率的交流信号实现无静差跟踪。因此，本文采用多谐振控制器能够实现对并网点电压谐波的抑制。

图6 多谐振控制器的Bode图Fig.6 Bode diagram of multi resonance controller

4 实验验证

为了验证本文所提方法的有效性，利用实验平台对其进行验证。系统硬件包括T型三电平逆变器主电路、LCL滤波器、直流稳压源、调压器以及控制板。其中，控制板由ARM芯片、CPLD芯片及相关系统配置所构成，ARM和CPLD芯片的型号分别为STM32F407ZG和EPM240T100C5N。首先通过在并网点与电网之间增加电感模拟电网阻抗的变化，修改电容电流反馈系数对比逆变器在电网阻抗存在时的控制效果；其次改变电网阻抗值，验证电容电流反馈系数修改方法的有效性；最后，在并网电压谐波存在时验证电压前馈方法的有效性。

图7为考虑电网阻抗前后的并网电流变化波形。由图中可以看出：当不考虑电网阻抗(图中前半部分）时，并网逆变器系统稳定运行；当考虑电网阻抗(如1 mH，图中后半部分）时，控制参数不变会导致系统不稳定。

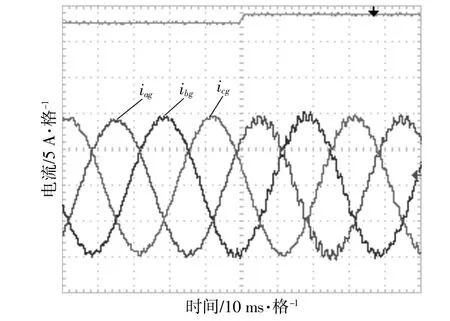
图7 考虑电网阻抗前后的并网电流变化波形Fig.7 Waveform of grid connected current changes before and after considering grid impedance

图8为考虑1 mH时的电网阻抗且改变H1后的并网电流变化波形。由图可以看出，采用本文所提方法改变电容电流反馈系数，系统能够重新达到稳定的状态。

图8 考虑1 mH的电网阻抗且改变H1时并网电流变化波形Fig.8 Change waveform of grid connected current when H1 is changed after considering 1 mH grid impedance

图9为电网阻抗为2 mH时的控制效果。图10为电网阻抗为3 mH时的控制效果。对于其他电网阻抗的值，采用本文的方法均能使系统稳定，不再重复叙述。

图9 考虑2 mH的电网阻抗且改变H1时并网电流变化波形Fig.9 Change waveform of grid connected current when H1 is changed after considering 2 mH grid impedance

图10 考虑3 mH的电网阻抗且改变H1时并网电流变化波形Fig.10 Change waveform of grid connected current when H1 is changed after considering 3 mH grid impedance

图11为并网点电压存在谐波时的并网电流波形。由图中可以看出，采用本文的多谐振控制器能够消除谐波对并网电流的影响。

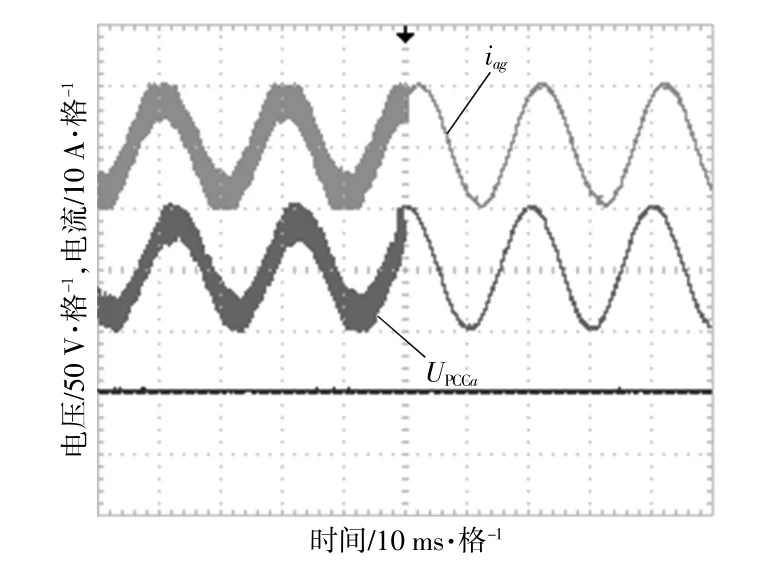
图11 并网点电压谐波抑制Fig.11 Harmonic suppression of voltage at parallel node

5 结语

弱电网存在并网点电压谐波与电网阻抗两个特征，均会对并网逆变器的稳定性带来影响。本文提出了采用变化的电容电流反馈系数应对电网阻抗，采用多谐振控制器消除并网点电压对并网电流谐波的影响。本文所提出的控制方法能够使并网逆变器在弱电网下安全稳定地运行。