基于等效风速的双馈风力发电机动偏心故障特性分析

绳晓玲，邓祖贤，万书亭，韩旭超，豆龙江，张 雄

(华北电力大学 电力机械装备健康维护与失效预防河北省重点实验室，河北 保定 071003）

0 引言

根据全球风能理事会(GWEC）发布的《2022年全球风能报告》[1]，2021年全球风电装机容量新增近94 GW。

风电行业蓬勃发展，大容量机型不断推陈出新，风力机大型化趋势愈发明显。叶片加长，塔筒加高，系统柔性也随之提升，这将使叶轮扫掠面内各点的风速差异与变化更为明显。这种差异主要是由风剪切、塔影效应以及湍流等因素导致，并且会随着时间和空间不断变化，简称为风速时空分布差异。

风速分布的差异性会进一步影响风电机组气动载荷，使得风电机组动态转矩、转速和偏航力矩等产生波动，也会导致机组功率损耗[2]和电力系统波动[3]。

本文选择双馈风力发电机的气隙偏心故障作为研究对象，对等效风速下的偏心故障特征进行分析。发电机正常运行时，定、转子间的气隙是均匀分布的。气隙偏心是发电机定子与转子间气隙空间分布不均匀的一种现象，约有90%的机械故障会导致气隙偏心。学者通过理论分析计算气隙磁场的变化，分析磁场特性，建立瞬态电磁场与多回路耦合的数学模型[4]，[5]来寻找偏心故障的电气特性。文献[6]通过建立时序电路模型来计算偏心量，并利用MATLAB/Simplorer进行电路联合仿真验证。文献[7]，[8]总结了双馈风力发电机气隙偏心的研究现状，给出了偏心故障特征频率的一般表达式。

针对风力发电机偏心故障的研究大多基于叶轮轮毂中心处的平均风速，由于未考虑风剪切、塔影效应等实际风速影响因素，分析的方法或者结果可能与实际有所偏离[9]。因此，本文首先研究了考虑风速时空分布的等效风速模型，然后基于等效风速模型研究双馈风力发电机气隙偏心故障特征的变化，并通过仿真与平均风速下的故障特征进行对比分析，最后用实验进行验证。

1 等效风速模型

本文针对叶轮扫掠面内的风速分布问题提出了普适的n-叶片等效风速模型来表示风速分布的时空差异，根据相关研究[2]，[9]，叶轮扫掠面内的等效风速VE可表示为轮毂平均风速VH、风剪切影响风速分量VQ和塔影影响风速分量VT之和。

式中：R为叶轮半径；H为轮毂高度；α为风剪切指 数；βb为 桨 叶 的 方 位 角；下 标b=1，2，3，分 别 代表3个叶片；D为塔筒半径；l为叶轮旋转平面到塔中心线的距离；ωY为叶轮转动角频率；r为分析点到风轮转轴的径向距离；M为轮毂风速与空间平均风速的转换差率。

对 式(2）和 式(3）化 简 得：

将 式(6），(7）带 入 式(1）并 化 简，得 到 等 效 风速的完整表达式。

根据式(8），绘制不同型号风力发电机在轮毂风速VH=11 m/s时的等效风速波动曲线(图1）。

图1 不同叶轮半径对应的等效风速曲线Fig.1 Equivalent wind speed curves for different impeller radii

使用MATLAB中的Fourier拟合工具对R=3 m时的风力机等效风速曲线进行拟合，结果见图2。

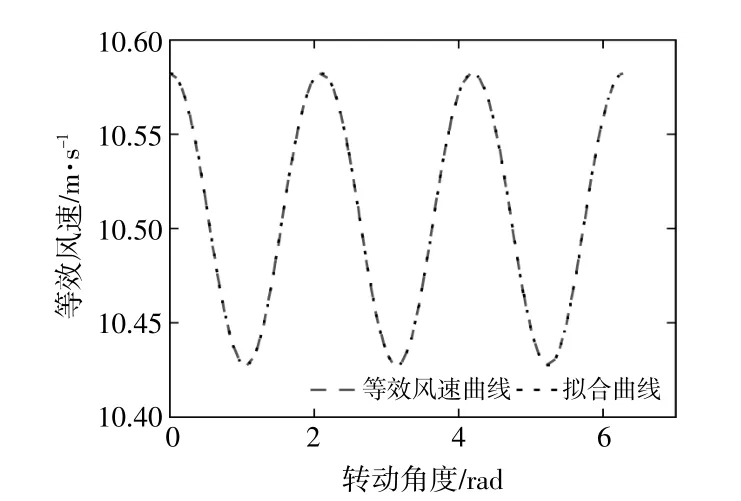
图2 风速曲线和拟合曲线Fig.2 Wind speed curve and fitted curve

图2中的拟合曲线表达式见式(9），式(9）中的参数见表1。

表1 拟合曲线参数Table 1 Fitted curve parameters

从图2可以观察到拟合曲线与原始风速曲线重合度非常高，a0值接近VH=11，拟合精度为1。其中x=ωYt。

因此，等效风速VE可近似为

式中：ak为风速第k项对应的系数。

2 机组特性分析

根据式(10）以及风力机输出机械转矩与风速二次方的正比关系，得到风力机输出的机械转矩T为

式中：T0为风机 气动 转矩 的稳 态 成 分 ，T0=0.5ρπR3CpV2H/λ；ρ为 空 气 密 度；Cp为 最 佳 风 能 利用系数；λ为最佳叶尖速比；Tk为转矩各谐波分量的幅值。

设角速度 ωY对应的频率为P，由式(11）可知，受等效风速的影响，风力机转矩也出现3kP的振荡波动。

双馈风力发电机的运动方程可表示为

式中：Te为电磁转矩；ωr为发电机转子角速度；J为机组的等效转动惯量。

根据式(12）可以得到双馈发电机的 ωr。

式中：ωr0为转子角速度稳态分量。

Ansoft中仿真的风力发电机功率为5.5 kW，叶轮半径为3 m，设两对极双馈发电机转子以vr=1 000 r/min正常运行，叶轮转动速度为60 r/min，则ωY=6.28 rad/s。根 据 式(9）～(13），由 表1中 的 风速拟合数据可以求得式(13）中电机角速度的各项附加参数，从而可以得到该转速下受等效风速影响的发电机波动转速，利用该波动转速可以在Ansoft中进行考虑等效风速影响的电机故障研究。

3 气隙偏心故障的影响分析

本文对动偏心故障下的电磁特性进行分析。双馈发电机动偏心简化结构如图3所示。

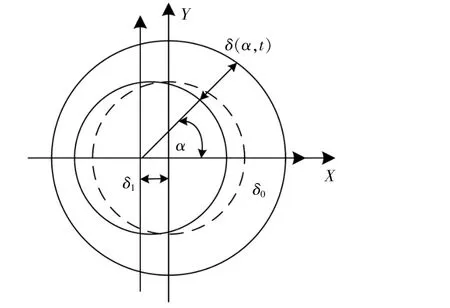
图3 动偏心简化示意图Fig.3 Simplified schematic of a dynamic eccentricity

图3中，δ1为转子旋转中心与转子几何中心的距离。以X轴水平方向为起点，得到气隙δ(α，t）随时间和转子转动位置变化的表达式：

式中：δ0为未偏心的平均气隙。

根据磁导与气隙之间的关系，并对其进行幂级数展开，忽略高阶分量，可得：

青岛中山路历史街区(以下简称中山路街区)位于青岛市南区中西部，西邻青岛火车站，南接栈桥公园.创始于1897年的德国占领时期，在改革开放以后逐渐萧条[1].天主教堂位于中山路的东侧山坡台地之上，塔身高56 m，是整个中山路街区的重要节点，构成中山路历史街区轮廓线的控制高度[2] (图1).

式中：μ为真空磁导率；Sδ为有效磁导面积；Λ0为未偏心下气隙磁导常值成分；Λ1为动偏心成分。

由磁路欧姆定律得到主磁通表达式：

式中：F为磁通势；ω1为风力发电机旋转磁场转速。

动偏心故障下的主磁通表达式中，出现了新的转速为 ω1±ωr的附加磁场。新的附加磁场将会导致定子绕组中出现对应频率的定子电流成分[10]。这部分定子电流会与基波磁通互相作用，导致主磁通受到相位调制，使定子电流中出现 ω1±kωr一系列成分。从结果而言，即转子动偏心故障下，定子电流受到了频率为转频fr的信号调制。

双馈风力发电机定子直接与电网相连，转子通过变流器与电网相连。当双馈发电机转速变化时，通过变流器调节馈入转子绕组的电流频率与相位，保持定子端输出频率稳定，即转子转频和转子励磁电流频率之和等于定子电流频率。

由上述分析可知，等效风速使发电机转子旋转频率中出现了3kP成分，导致转子绕组中励磁电流产生相应频率的波动。为了获得稳定的机电能量转换，并使定子与转子之间的旋转磁场保持相对静止，转子绕组中的谐波又会在定子绕组中感应出对应的谐波。因此，发电机定子绕组中也应存在调制频率为3kP的磁场分量。

等效风速下电机主磁通可表达为

式中：ck为系数Tk/(3kJωY）在定子中引起的波动系数。

式 中：dk=Tk/(3kJωY）。

引入等效风速后，动偏心故障下发电机主磁通的频率成分非常复杂，必然导致定子电流成分也发生相应变化。在定子电流频率中除了基频 ω1和偏心故障特征频率 ω1±k1ωr0之外，在这些频率的附近均会出现3kP的调制边带，也即 ω1±3kP和 ω1±ωr0±3kP，以及前两者进一步相互作用产生的 频 率 ω1±k1ωr0±3kP。

4 仿真及结果分析

为验证理论分析的正确性，在Ansoft中搭建了双馈风力发电机的2D仿真模型，模型结构如图4所示，参数见表2。

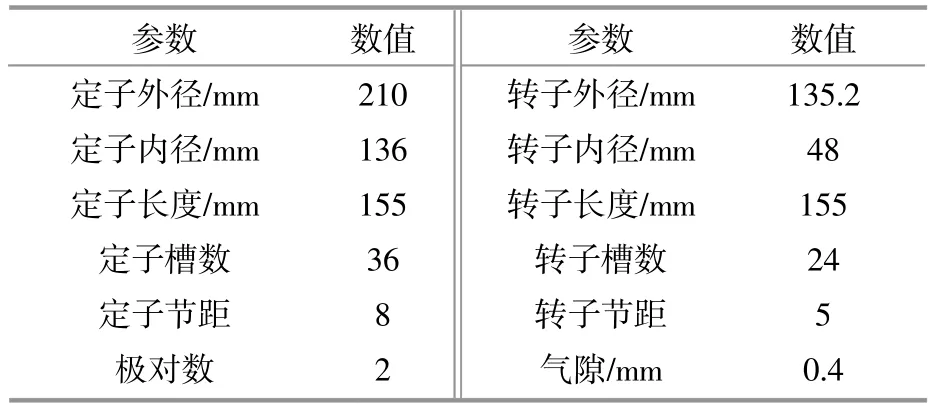
表2 模型参数Table 2 Model parameters

图4 风力机2D模型Fig.4 2D model of a wind turbine

对该双馈风力发电机模型分别进行正常工况、动偏心工况和等效风速叠加动偏心工况下的仿真，发电机转子转速为1 000 r/mim，采样频率为5 kHz。采集定子电流数据，并对结果进行功率谱密度(PSD）分析。正常运行的定子电流频谱见图5(a），单独添加动偏心故障(偏心距离为0.15 mm）情况下的定子电流频谱如图5(b）所示。由图5可知，偏心故障下，定子电流频率中出现了f±fr和f±2fr成分，符合理论推导中动偏心故障下定子电流新增f±kfr频率成分。

图5 定子电流PSD谱Fig.5 PSD spectrum of stator current

根据前述理论分析，将转子转速设置为受等效风速影响的转速，然后进行动偏心叠加等效风速工况下的仿真，结果如图6所示。

图6 等效风速影响下的动偏心故障定子电流频谱(0.15 mm）Fig.6 Dynamic eccentric fault stator current spectrum under the influence of equivalent wind speed(0.15 mm）

由图6可知，定子电流基频f附近出现由等效风速引起的f±3kP频率成分，动偏心故障特征f±2fr频 率 成 分 十 分 明 显，且 附 近 出 现f±2fr±3kP的频率成分，即仿真结果与理论推导一致。在此基础上，将动偏心增加到0.18 mm，重复实验，结果如图7所示。

图7 等效风速影响下的动偏心故障定子电流频谱(0.18 mm）Fig.7 Dynamic eccentric fault stator current spectrum under the influence of equivalent wind speed(0.18 mm）

为了进一步观测不同叶轮角速度下等效风速的影响，在0.15 mm偏心故障仿真基础上，将叶轮角速度设置为之前的一半，即 ωY=3.14 rad/s，转子转速不变，重新拟合等效风速，并进行仿真，处理后的结果如图8所示。

图8 等效风速影响下的动偏心故障定子电流频谱(0.15 mm，ωY=3.14 rad/s）Fig.8 Dynamic eccentric fault stator current spectrum under the influence of equivalent wind speed(0.15 mm，ωY=3.14 rad/s）

与图6相比，图7中的故障特征频率成分更为突出，且等效风速所引起的3kP调制边带十分明显。在图8中，能观测到动偏心故障特征频率成分，与图6相比，横轴上3P的值明显减小，等效风速引起的3kP调制边带更加密集，符合理论推导。

等效风速和动偏心故障均对发电机主磁通产生了影响，于是导出定子绕组的磁链数据，并对其进行处理，绘制其频谱(图9）。由图9可知，在等效风速影响下，动偏心故障的定子绕组磁链中出现了较为明显的动偏心故障频率成分f+2fr和f+4fr，且这两个频率周围也有3kP的边带，与理论推导吻合。

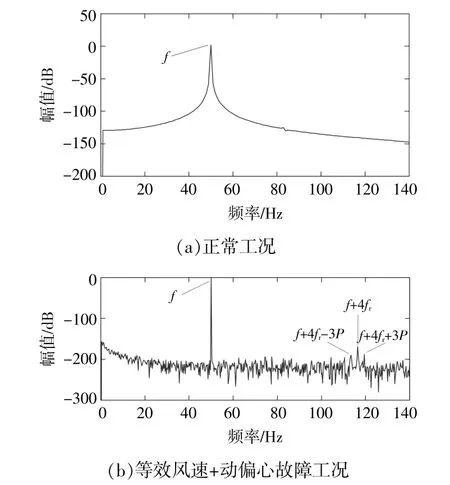
图9 磁链PSD谱Fig.9 Flux PSD spectrum

5 实验及数据分析

为了更进一步验证理论推导与仿真的正确性，本文利用双馈风力发电机实验台进行等效风速影响下的转子动偏心故障实验。图10为双馈发电机及偏心调节装置，在发电机转子加长部分切割了一段槽。

图10 发电机及气隙偏心故障模拟装置Fig.10 Generator and the air gap eccentricity fault simulation platform

正常运行时，这段切槽的转子在发电机定子的外侧。需要模拟动偏心故障时，通过图10所示的螺栓，推动发电机定子，使切槽的转子进入到定子，模拟定转子之间的动态气隙偏心。

本次实验模拟的 ωY值设定为1.05 rad/s，并在此转速基础上生成等效风速曲线。对应的3P值为0.5 Hz，发电机转子转频fr为20 Hz。采样频率为10 000 Hz，采样时间为20 s，将采集的定子电流数据进行处理并绘制频谱图(图11）。由图11可知：在基频50 Hz附近出现了因等效风速周期性波动导致的3kP边带；图11(b）中动偏心故障特征频率f-fr较为明显，且附近存在一系列3kP成分；图11(d）中f+fr频率成分不明显。

图11 实验台定子电流PSD谱(1.05 rad/s）Fig.11 Stator current PSD spectrum of test rig(1.05 rad/s）

在图11所示实验结果的基础上，又增加一组叶轮角速度ωY为0.525 rad/s的实验，并重新拟合等效风速。对应的3P值为0.25 Hz，发电机转子转频fr为10 Hz，实验结果如图12所示。

图12 实验台定子电流PSD谱(0.525 rad/s）Fig.12 Stator current PSD spectrum of test rig(0.525 rad/s）

由 图12可 以 观 察 到f±fr，f±2fr，f±3fr，以 及 周围的3P边频带，结果与图11基本类似。但与图11相比，随着叶轮角速度的降低，等效风速所引起的3P数值随之减小，3kP边带也随之变得更加密集。实验结果与理论推导和仿真结果吻合。

6 结论

本文从等效风速和双馈风力发电机组动偏心故障的机理出发，通过理论推导、仿真分析以及实验验证，得出以下结论。

①实际风况中的风剪切和塔影效应影响风力机的气动特性，造成气动转矩和转速波动，并进一步通过传动部件影响到发电机转子转速，导致电机电磁参量发生变化。

②考虑等效风速后，动偏心故障特征发生变化，且比较复杂。在定子电流中，除了定子电流基频外，还有动偏心特征频率转子转频、等效风速所引起的3kP调制频率以及上述频率的相互耦合产生的新频率。研究结果为实际工况下的动偏心故障诊断和监测提供了一定的理论依据。