基于VMD-STFT提升源-荷互动可靠性的混合储能优化配置
马永翔,唐浦容,闫群民,李宏刚,淡文国
(1.陕西理工大学 电气工程学院,陕西 汉中 723001;2.成都市水利电力勘测设计院有限公司,四川 成都610000;3.乌兰察布电业局,内蒙古 乌兰察布 012000)
0 引言
以风能、太阳能为代表的分布式可再生能源发电技术得到了众多青睐。微电网可以克服可再生能源发电的波动性、随机性。当微电网处于孤岛运行状态时,由分布式可再生能源构成的发电系统输出功率与负荷所需不能完全一致,导致独立运行的微电网内源荷两端匹配度较差[1]~[3],在负荷高峰和发电低谷时刻无法保证负荷的持续可靠供电,而储能系统能够有效解决这一问题[4]。
常见的储能元件可分为功率型储能和能量型储能。两种储能混合的方法可弥补单一储能的不足,是当前保证系统中能量供需平衡的重要手段[5]。文献[6]采用两种类型储能结合的混合储能系统,实现了微电网处于孤岛运行状态时的内部功率平衡。文献[7],[8]分别以系统总成本和电压偏移率最低作为优化目标,对风力发电和风光发电系统的储能容量配置进行寻优。文献[9]~[11]除将成本作为配置目标外,还分别在提高可再生能源利用率、系统供电可靠性和平抑联络线功率波动方面进行储能的优化配置。上述文献大多明确优化目标再进行储能的配置,也可先将参考功率进行分解,再各自分配给储能元件。文献[12],[13]使用低通滤波算法对微电网储能系统进行优化配置。文献[14],[15]使用EMD分解风电功率并配置混合储能,实现功率的平滑吸收。文献[16],[17]基于VMD,通过混合储能的容量配置分别平抑净负荷和风电出力的功率波动,但在确定分层数和分频界限的方法上还需要进一步考虑。有关微电网混合储能配置方面的问题,优化目标各有不同,配置方法也有新的研究成果,针对各种分解功率的方法,传统滤波法的时间常数难以确定,存在分解不彻底的问题。EMD法本身存在较严重的模态混叠问题,对功率的剖分效果不理想。VMD法可通过控制收敛条件,有效处理频率相近的信号,但在确定分层数和分量重构依据方面需要进一步的处理。
在实际工程应用中,对需求侧用电趋势进行分析预测后,再根据不同的需求进行混合储能配置也具有一定的现实意义。本文以储能配置成本和供电可靠性两个指标作为优化目标,提出使用确定最优分层数K的VMD法结合STFT对微电网需求侧混合储能系统进行优化配置,并验证了本文配置方法相较于其他两种传统方法的优越性。
1 独立微电网系统结构
1.1 直流微电网拓扑结构
本文含有混合储能的独立直流风、光发电微电网系统结构如图1所示。

图1 含混合储能的直流微电网结构图Fig.1 Structure diagram of DC microgrid with hybrid energy storage
1.2 混合储能系统
为克服光伏及风力发电的间歇性、随机性对负荷正常供电的影响,加设储能系统能够保证独立微电网的持续稳定运行[18]。在微电网中发挥功率型储能和能量型储能的优越性能,能有效的抑制功率短时间波动,延长储能的使用寿命。
1.2.1容量计算
本文功率型储能装置选用响应速度快的超级电容,能够对负荷突变提供瞬时的功率支撑,提供功率波动中的高频分量。能量型储能装置则选用储能时间长,且能量密度较大的铅酸蓄电池,用以平抑功率中的低频波动分量[5]。
在系统的整个工作过程中,净负荷功率为
式 中:PLoad(t)为 负 荷 功 率;PSolar(t)为 光 伏 发 电 的 有功功率;PWind(t)为风力发电的有功功率。
当P(t)>0时,表示储能系统需要提供的功率;当P(t)<0时,表示储能系统需要存储的功率。
根据已知储能装置每个采样时刻所需提供或消纳的有功功率P(t),高频分量记为PS(t),低频分量记为PB(t),可以得到从t0时刻起整个采样时间T中累积的总功率ΔP,总能量ΔE为
式 中:ΔPS,ΔPB,ΔES,ΔEB分 别 为 超 级 电 容 和 蓄 电池累积的总功率和总能量。方便后文描述,本文下标S统一指代高频分量,即超级电容的相关值;下标B统一指代低频分量,即蓄电池的相关值。
1.2.2可靠额定容量计算
计算储能装置的额定容量及功率须采用可靠容量计算方法。对设计储能装置额定功率的要求是须满足整个采样周期内等效净负荷最大值。在实际应用中,还应考虑电池的荷电状态(SOC),以保护储能元件并且延长其使用期限,设定超级电容SOC上、下限SOCminS,maxS和蓄电池的SOC上、下 限SOCminB,maxB。
经过储能的SOC约束后,可得到储能元件的额定功率为[19]
式 中 :Pdis,S/B,Pch,S/B分 别 为 储 能 装 置 的 实 际 输 出 和吸收功率。
能量型储能的额定容量为[19]
式 中:Edis,S/B,Ech,S/B分 别 为 储 能 装 置 的 实 际 放 电 电量和充电电量。
功率型储能的额定容量主要取决于其快速响应 特 性[19]。
式中:Δt为能量型储能滞后于功率型储能的时间差,可 取0.5 s。
由于能量型储能追踪电流指令慢于功率型储能的响应时间,在其时间差内会出现实际承担的最大电量值,故而在能量型储能捕捉到电流指令后,二者才会根据分频后负责的功率大小各自正常运行。
2 混合储能功率分配方法
根据两种储能装置互补的特性,可使用3种不同的分频方法。
2.1 变分模态分解
2.1.1变分模态分解原理
在处理变非线性、非平稳的波动信号方面,分模 态 分 解(Variational Modal Decomposition,VMD)是一种自适应的信号分解方法[20]。使用VMD分解净负荷功率序列信号再分配给混合储能,能够提高微电网需求侧的供电可靠性及配置经济性。整体的VMD法分解信号序列思路是将信号分解成K个具有固定中心频率 ωk的模态分量uk[21]。分解层数需要预先设置,若选取较小的K值,信号序列中的一些重要信息会被过滤,影响分解精度;当选取的K值较大,相邻模态分量的中心频率会过于接近,导致模态分量重复。为找出合适的分解层数从而得到准确的分解结果,本文采用中心频率法确定最优分层数K,同时为了防止出现通频带重合、模态混叠等现象,采用皮尔逊相关系数法(Pearson)进一步确定K。
2.1.2基于短时傅里叶变换(STFT)的分量重构
为研究各分解模态间的混叠情况,同时作为分量重构的依据,本文采用短时傅里叶变换的方法对序列信号进行时频分析,短时傅里叶变换将时域和频域联系起来,实质是对傅里叶变换的加窗处理,对信号进行分段的频谱分析,从而得出信号的时变信息[22]。通过STFT能够得出各分量信号频率随时间变化的情况、各时刻的瞬时频率及幅值。对使用了VMD分解的模态分量利用STFT进行时频分析,可得到各模态的混叠情况,同时根据不同类型储能元件的频率响应特性进行分量的重构和配置,以提升系统的性能。
2.2 经验模态分解
经验模态分解技术(EMD)能够无需任何先验信息,根据采样时间的不同尺度特征,将含有多个频率成分的原始信号分解为一系列的单频率信号,也即本征模态函数(Intrinsic Mode Function,IMF)[23]。当采用EMD对净负荷功率P(t)进行分解后,余量反映P(t)变化趋势,每个IMF都是P(t)的一种振荡模式,整个分解得出的IMF分量及一个余量的总和等于原始数据P(t)[20]。
在使用EMD分解法时,若输入信号存在间歇现象,则会导致分解结果模态混叠,造成信号时频分布错乱,得到不准确甚至错误的IMF分量,因此采用STFT分析的模态混叠情况并作为分量重构的依据。以开始发生混叠现象的分量为界,对功率进行高、低频的重构并合理分配给超级电容和蓄电池。
2.3 一阶低通滤波
低通滤波同样可以作为分解信号的方法,低频信号可以正常通过,而高频的超过设置临界值的信号被阻断或是减弱[24]。使用一阶低通滤波法对本文净负荷功率进行分配的具体过程是:净负荷功率P(t)经滤波后,得到低频分量PB(t),用滤波前的功率减去PB(t)得到高频分量PS(t)。使用一阶低通滤波算法后的高、低频功率分量表达式为[20]
由式(7)可知,TL的取值影响功率的分配情况[25],TL取值越大,低频分量波动幅度就越小,意味着蓄电池承担的功率分量较为平稳,而高频分量波动则较为剧烈,表示超级电容承担波动幅度较大的功率分量;相反,若TL取值越小,蓄电池承担的功率波动幅度会变大,而超级电容承担的功率波动幅度变小。为避免蓄电池频繁充放电,同时发挥超级电容的较快响应速度优点,在时间规定范围内,尽量取较大的滤波时间常数,同时,TL与分界频率fL[0~1/(2ts)]呈负相关特性,故选择较小的fL值,本 文 取0.5。
3 配置优化指标
在对混合储能进行配置时,不同的功率分频方法在不同方面也会呈现出各自的优势,本文给出以下几种评价指标,为实际应用中的不同需求提供参考。
3.1 混合储能投资运行成本
在配置混合储能时,由于超级电容和铅酸蓄电池的使用寿命周期不同,为防止其差异性给经济计算带来偏差,采取净年值法将购置成本折算为等年值。体现系统经济性的指标通常包含储能装置的购置成本、更换成本及维护成本[12]。
3.1.1购置成本
购 置 成 本Cg,S,Cg,B由 储 能 装 置 各 自 的 额 定 功率和额定容量决定,同时也与其必要的辅助设施成 本 相 关[12],即:
式 中:CE,S,CE,B分 别 为 超 级 电 容 和 蓄 电 池 的 单 位能量价格,本文分别取37 000元/(kW•h)和1 240元/(kW•h);ηe为 储 能 元 件 充 放 电 效 率,取0.85;Cp,S,Cp,B分 别 为 超 级 电 容 和 蓄 电 池 的 单 位 功 率 价格,分 别 取370,1 100元/kW;Cf,B为 蓄 电 池 辅 助 设施的单位能量成本,取350元/(kW•h);R为与项目周期及年利率相关的等年值折算系数,本文取0.117。
3.1.2更换成本
超 级 电 容 及 蓄 电 池 的 更 换 成 本Ch,S,Ch,B为[12]
式中:kS,kB分别为超级电容和蓄电池的更换次数;β为更换序数;q为储能装置的寿命周期,设置超级电容寿命20 a,蓄电池寿命5 a。
3.1.3维护成本
超 级 电 容 及 蓄 电 池 的 维 护 成 本Cw,S,Cw,B与 额定功率有关,包含人力管理成本[12],即:
式 中:Cz,S,Cz,B分 别 为 超 级 电 容 和 蓄 电 池 单 位 功 率下的维护成本,分别取50,30元/kW。
3.2 储能装置荷电状态
SOC反映装置的剩余容量[26]。计算整个采样周期某一时刻的储能SOC(t)为
式中:SOC(t-1)为上一时刻的SOC,初始SOC(0)取0.5;E(t)为t时储能需提供或消耗的容量;整个采样周期T内,储能需累积提供的最大或最小能量(若为负值,取绝对值);本文超级电容和蓄电池的SOC上、下限分别取0.1≤SOCS≤0.9,0.15≤SOCminS≤0.85。
3.3 系统供电可靠性评估指标
本文以系统的缺电时刻占总采样时间点的百分比作为评估系统供电可靠性的指标,即缺电概率(Loss of Power Supply Probability,LPSP)。当 发电系统提供的电能不足以承担负荷用电量,且储能系统也达到了放电上限,则此时的负荷处于缺电状态。本文将已知净负荷功率分解后再分配给储能,当采用的储能配置方案分析系统的缺电概率时,需要根据设定的SOC上、下限来判断。为描述整个采样周期的缺电情况,定义一个布尔量SLPSP。若某一时刻t超级电容及蓄电池的SOC均等于或低于设置的最小值,判定此时刻负荷处于缺 电 状 态,则SLPSP(t)=1,其 余 不 缺 电 时 刻SLPSP(t)=0。缺 电 概 率(LPSP)为
式中:T为整个采样周期总采样点数。
3.4 系统消纳水平评估指标
本文以系统的能源弃用率(Loss of Produced Power Probability,LPPP)作为评估系统光伏及风力发电消纳水平的指标。能源弃用是指风光发电系统提供的电能充足,不仅可为负荷提供电能,同时为储能充电,但储能系统达到了充电上限,此时不得不将多余的风电光伏发电资源舍弃。本文判断系统是否处于弃风弃光状态,同样依据储能系统的SOC值。为描述整个采样周期的能源弃用情况,定义一个布尔量SLPPP。若某一时刻t超级电容及蓄电池的SOC值均高于设置的最大值,判定此时刻储能饱和,系统处于能源弃用状态,则SLPPP(t)=1,其余时刻SLPPP(t)=0。能源弃用率表达式为
混合储能优化配置整体框图如图2所示。
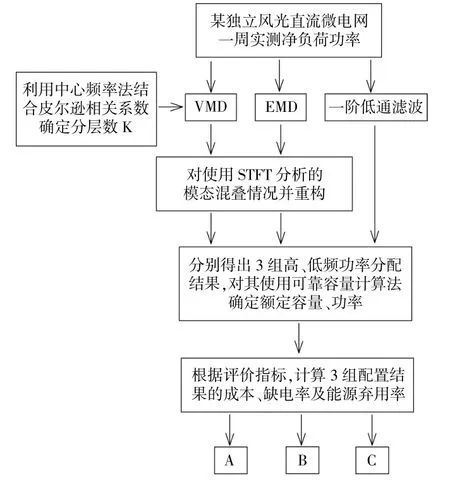
图2 混合储能优化配置整体框图Fig.2 Overall block diagram of hybrid energy storage optimization configuration
4 算例分析
本文基于某独立风光直流微电网一周的实测数据进行仿真实验。该微电网光伏发电系统额定功率为250 kW、风力发电系统额定功率为200 kW、系统最大负荷为300 kW,P(t)为净负荷功率,取一周的功率数据,采样时间ts均为15 min,假设项目周期为20 a,风光发电单元总功率及负荷功率曲线如图3所示。

图3 负荷及风光发电单元功率曲线Fig.3 Load and wind turbine units power curve
对负荷功率及发电单元功率作差,得到净负荷功率数据P(t),也即混合储能参考功率,如图4所示。

图4 净负荷功率曲线Fig.4 Net load power curve
4.1 方案设计
使用VMD分解法时,需要预先确定模态数K,K值过大或者过小都会影响分解结果,导致分解不完全或产生混叠现象。本文通过观察不同分解模态数时的中心频率分布确定最优的K值,对应K值的中心频率如表1所示。

表1 不同K值对应的中心频率Table 1 Center frequency corresponding to different K
由表1可知,当K值为7时,中心频率稳定在0.480 7,但观察分解结果0.242 6,0.327 7及0.480 7 Hz的3个频率相差较小,有可能出现通频带重合导致的模态混叠现象。为了进一步确定合理的模态数,本文使用Pearson相关系数法将相邻模态分量的相关性进行分析比较,如表2所示。

表2 相邻模态分量的Pearson相关系数Table 2 Pearson correlation coefficient of adjacent modal components
表中Cnm为分解出的第n和m个模态分量的相关系数,取值为-1~1,当所得数值越接近于1,表示两组变量趋于正相关的程度越高;越接近于-1,表示负相关程度越高;接近于0,表示线性相关度低[23]。当K<6时,相邻分量的相关系数均小于0.06,而K=7时,相关系数值较大,甚至C67超过0.1,表明当选定的模态数≥7时,分解出的模态分量相关性较高,易出现混叠现象。
本文选定K=6不仅满足中心频率的稳定,各相邻模态分量耦合程度也较低。VMD分解的参数α选用默认值2 000;τ设置为0.3,以保证信号序列分解的保真度。经VMD分解后的净负荷序列信号结果如图5所示。
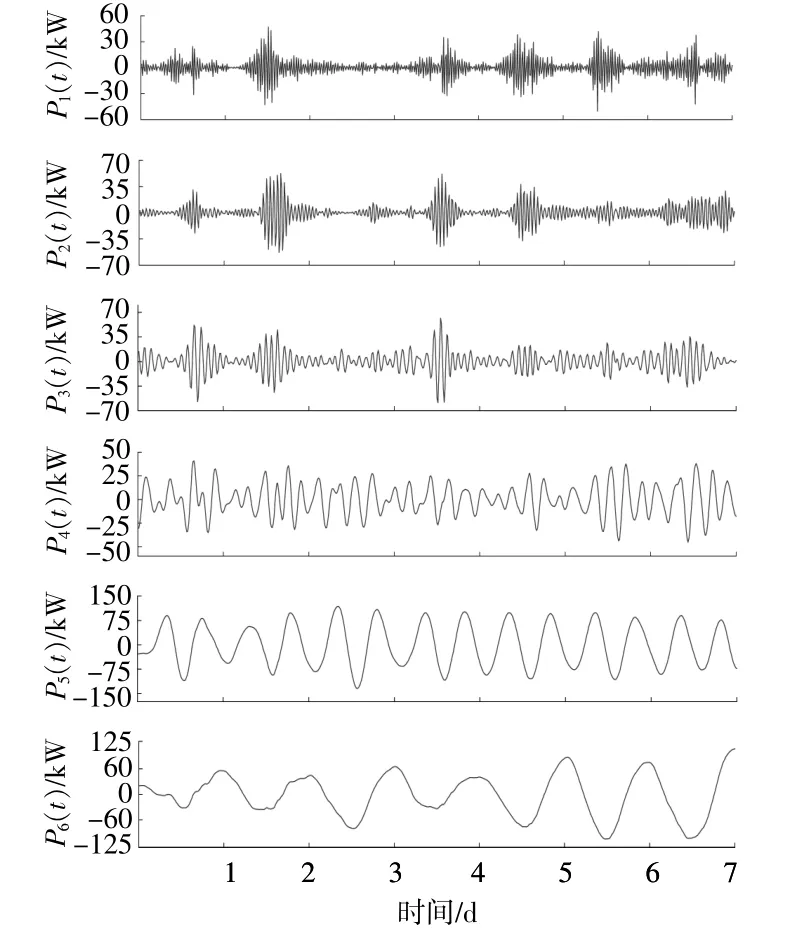
图5 基于VMD的净负荷功率分解结果Fig.5 Power decomposition of net load based on VMD
图中P1(t)~P6(t)分别为从高频到低频的功率分量IMF1~IMF6,虽能明显看出高、低频功率波动幅度的较大差异,但进行高、低频功率重构需要进一步通过STFT进行时频分析,并根据储能装置的频率响应特性进行功率的配置。
4.2 结果对比分析
为了对储能的功率进行配置,需要对分配结果进行重构。本文利用STFT分别对使用VMD及EMD分解后的各模态分量进行时频分析,结果如图6,7所 示。
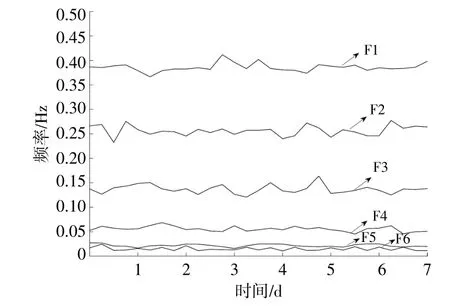
图6 经STFT分析后得到的VMD分解结果瞬时频率时间曲线Fig.6 The instantaneous frequency-time curve of VMD decomposition results obtained after STFT analysis

图7 经STFT分析后得到的EMD分解结果瞬时频率时间曲线Fig.7 The instantaneous frequency-time curve of EMD decomposition results obtained after STFT analysis
由图6,7可知,分量的时频分析曲线有重合部分,说明分解出的分量耦合程度较高,产生了模态混叠现象,同时根据选用的混合储能装置的性能差异,使超级电容承担频率较高、波动较为剧烈的高频分量;而蓄电池承担频率较低、波动较平稳的低频分量。对使用了VMD分解法的分量IMF1-IMF4重构、IMF5和IMF6重构,使用EMD分解法的分量IMF1和IMF2重构、IMF3-IMF8重构,最后进行不同储能装置的功率分配。分别用3种分配方法重构后的高、低频分量结果见图8~10。

图8 使用VMD分解后的净负荷功率分量Fig.8 Power component of net load after VMD decomposition
对比图8~10可知,经VMD和EMD分解后的低频功率分量更为平稳,分量曲线无明显尖峰,表明这两种分频技术很大程度上将功率按照频率波动的特性进行了分解。而经一阶低通滤波方法滤出的高、低频功率分量波动都较为明显,蓄电池会承担较多功率分量,不利于延长蓄电池寿命。
应用不同的分频方法,得到的配置结果也不相同。经过计算,3种方法下的系统缺电率、能源弃用率、配置总成本等结果如表3所示。

表3 混合储能系统配置结果对比Table 3 Comparison of hybrid energy storage system configuration results
由表3可知:使用一阶低通滤波方法虽然成本较低,但无法保证对负荷的可靠供电,能源弃用率也较高,结合图9,低频分量各时刻波动幅度较剧烈,表明蓄电池在工作过程中需要频繁的充放电,此举也不利于延长电池的使用寿命;使用EMD分解技术得出的储能配置结果在采样周期内无缺电时刻且能源弃用率降为1.79%,表明供电可靠性和能源消纳水平均略高于使用一阶低通滤波法,但所需的配置总成本高出47万元;而使用VMD法的配置方案不仅保证了系统的可靠供电,能源弃用率低至0.59%,配置总成本相较于3种方法中最经济的一阶低通滤波法也减少了23万元,表明此配置方法在能源消纳水平及经济性方面均有一定的优化效果,不同程度上提升了源-荷互动的灵活性和可靠性。

图9 使用EMD分解后的净负荷功率分量Fig.9 Power component of net load after EMD decomposition

图10 使用一阶低通滤波分解后的净负荷功率分量Fig.10 Power component of net load decomposed by firstorder low-pass filtering
5 结论
本文基于含有混合储能系统的独立直流微电网,提出了使用VMD分解法结合STFT的储能优化配置方案。首先利用系统的发电功率以及负荷功率数据得出微电网系统的净负荷功率,再根据储能装置的特性,采用超级电容和铅酸蓄电池作为系统的混合储能部分;然后分析VMD,EMD分解技术和一阶低通滤波方法的原理,其中,使用中心频率法结合皮尔逊相关系数确定VMD的最优分解模态数K,再通过STFT对EMD和VMD的分解结果进行时频分析,研究各分量的模态混叠情况并作为分量重构的依据。将使用以上3种方法得出的分解结果重构后分配给超级电容和蓄电池,最后对总配置成本、缺电率和能源弃用率等指标进行计算对比,从经济性和供电可靠性两方面体现了使用VMD分解法配置储能的优越性,也进一步提高了源-荷互动的灵活性,可为实际的工程项目应用提供参考。

