具备启发式路径优化的机械臂路径规划算法
邓鈃中 张伟军
(上海交通大学机械与动力工程学院,上海 200240)
0 路径规划算法发展现状
如今,机械臂和移动机器人在许多领域扮演着重要角色。移动机器人被广泛应用于未知环境的探测[1]、导航、定位[2]和制图等[3]。多关节机械臂在制造业领域发挥着重要的作用,能够完成搬运,组装和加工等任务。它们不仅能提高生产效率和产品质量,还能减少人力成本和操作风险。路径规划是一项必要而关键的技术,能帮助机器人在这些任务中更加高效智能地完成任务。
为解决路径规划问题,需要在给定状态空间中找到一条连接起始点和目标点的路径并保证路径不会与任何障碍物发生碰撞。从1970年开始,学术界涌现了各类路径规划算法包括基于搜索的算法、基于采样的算法、基于人工势场的算法。各类算法在不同场景各有优势[4-9],算法的耗时和路径的距离通常是评价该算法最有效的指标。基于搜索的算法如A*[10]和Dijkstra[11]算法需要把问题的状态空间划分成网格,所以基于搜索的算法的效率和可行性依赖于网格的划分,并且很难适应不同问题中状态空间的维度变化。
基于人工势场的算法APF的路径规划方法通过引力和斥力势场来实现机器人的导航和避障,根据环境感知实时计算势场,适用于动态环境中的移动物体。基于人工势场算法在构建地图势能场时需要获知全局地图,但这在机械臂运动的高维状态空间中是相当困难的。基于人工势场算法容易陷入局部最小值和陷阱,难以完成复杂环境中的规划任务。
基于采样的规划算法如RRT[12]通过在问题状态空间中采样增量式构建一个以机器人初始点为根节点并向无障碍可达空间扩展的搜索树。通过对状态空间的随机采样将极大降低算法的时间复杂度。基于采样的规划算法适用于高维状态空间的路径规划并能方便地扩展到不同维度的问题中。RRT能在大多数场景中高效地找到路径,但搜索时间和路径距离仍然存在较大优化空间。研究人员基于RRT提出了许多改进。改进的方向大概分为两类,即初始路径前优化OBIP(Optimize before Initial Path)和初始路径后优化OAIP(Optimize after Initial Path)。OBIP意味着在找到初始路径前或在寻找初始路径过程中进行优化。RRT*[13]在构建搜索树的过程中对新节点执行“Rwire”步骤能帮助新节点找到代价更低的父节点以进一步减小路径代价。RRT-Connect[14]算法分别以起始点和目标点为根节点生成两棵搜索树,当两棵树互相连接时认为路径规划成功,其中的启发式步骤极大加快了搜索速度,并在狭窄路径场景中表现出优异性能。FMT*[15]算法采用先采样,后连接的方法完成路径规划,添加新节点时只会发生一次碰撞检测,是一种更快的渐近最优路径规划算法。通常来说,想要一次性找到最优路径是比较困难的,OAIP意味着在找到初始路径后再对路径进行寻优。Informed RRT*算法利用RRT*算法找到初始路径,再根据初始路径划分出超椭球子集作为后续采样空间,Informed RRT*通过缩小采样空间的方法加快了路径的寻优速度[16]。RRT*-Smart[17]算法在RRT*算法基础上提出了智能采样和路径优化方法,在找到初始路径后快速寻优得到近似最优路径。BIT*[18]算法吸取了RRT*、Informed RRT*和FMT*算法的特点,使用多批多点采样方法和有序搜索方法提高了搜索效率。
为了尽可能搜索得到一条代价更小的路径,我们引入了Informed RRT*SR(Informed RRT*with Smart Rope)算法。基于Informed RRT*的工作,Informed RRT*SR能够高效地在高维空间中搜索到无碰路径,并通过在无碰路径附近的状态空间进行启发式探索对无碰路径进行进一步优化。Informed RRT*SR继承了Informed RRT*高效搜索的优点,并利用路径优化算法克服了路径蜿蜒曲折的缺点。在路径优化阶段,相比于其他基于采样的对状态空间进行完全随机搜索的路径探索算法,具备启发式探索规则的Informed RRT*SR能更有针对性地探索状态空间从而减少路径搜索时间。Informed RRT*SR通常能找到一条更快捷的无碰路径,且路径的转折点能很好地适应障碍物的外形。本文首先描述了通篇使用的Informed RRT*SR的符号和算法描述,给出了基于采样算法和Informed RRT*SR在实际问题中的仿真结果。
1 算法描述
1.1 算法符号说明
路径规划问题的目标是在状态空间中找到一条连通起始点和目标点的无碰路径,这条连续的路径被表示为P=(V,E),此处V表示路径中的节点,E⊂V×V代表连接两个节点的一条边。每个节点V均属于n维路径规划问题的状态空间,表示为X⊂n。在机器人路径规划问题中,n则代表机器人构型空间的维度数目。在路径规划问题的状态空间中存在的障碍表示为Xobs⊂X,无障碍空间则表示为Xfree=XXobs。
判断碰撞:函数Obstaclefree(xa,xb)用于判断Xline⊂Xfree是否成立,Xline的定义是公式1。
Xline={x|x=αxa+(1-α)xb,α∈[0,1]}
(1)
节点无碰连接检测:Connectfree(xi,xj,xk)表示对从xi、xj到xk,依次直接相连接的路径进行碰撞检测,如果全程没有碰撞则返回真,否则返回假。
空间取基:Base(A)表示取得向量空间A的所有基向量。
计算路径:Dist({A,B})表示计算由A和B组成的边的距离。
回溯路径:getPath(x)表示从节点x开始回溯得到路径P。
取路径终点:getEnd(P)表示取得路径P的终点x。
算法中的Cost、Sample、Nearest、Steer、Line、Parent、InGoalRegion函数均沿用于Informed RRT*论文[16]。

表1 Informed RRT*SR算法
Informed RRT*SR算法在Informed RRT*的基础上引入了路径优化步骤。算法1中的Line1-Line36为Informed RRT*算法。算法1中的Line38-42表明在Informed RRT*算法搜寻得到无碰路径后对该路径进行进一步优化以缩短路径距离。Informed RRT*算法依赖迭代过程中搜寻得到的最短路径的距离以压缩算法后续的搜索空间,在算法迭代过程中尽可能找到更短的路径能加速算法的搜索速度。Informed RRT*SR中的路径优化步骤能有效对路径距离进行优化,从而在相同时间内搜索到更短的无碰路径。
1.2 路径优化
算法1中的Line39代表路径优化的核心算法。SRTL(Smart Rope-Tightening-Loosening)算法的具体实现见算法 2。SRTL算法负责将得到的无碰路径进行进一步的优化。SRTL包含循环执行n次的两个步骤,即路径收缩SRT和路径松弛SRL。

表2 SRTL算法
1.3 路径收缩
路径收缩SRT(Smart Rope-Tightening)的作用是将无碰路径收缩,能有效缩短无碰路径的距离,其算法实现见算法 3。在算法 3中,Line2代表对路径的每个一节点进行遍历。Line4和Line5在边线{Xi-1,Xi}和{Xi,Xi+1}中分别取点得到Xleft和Xright。Line6到Line14尝试直接连接Xleft和Xright得到新的路径,如果该路径是无碰的,则对路径中节点和边线进行修改。

表3 SRT算法

表5 SRL算法

表6 MOVE算法

表7 FIND算法
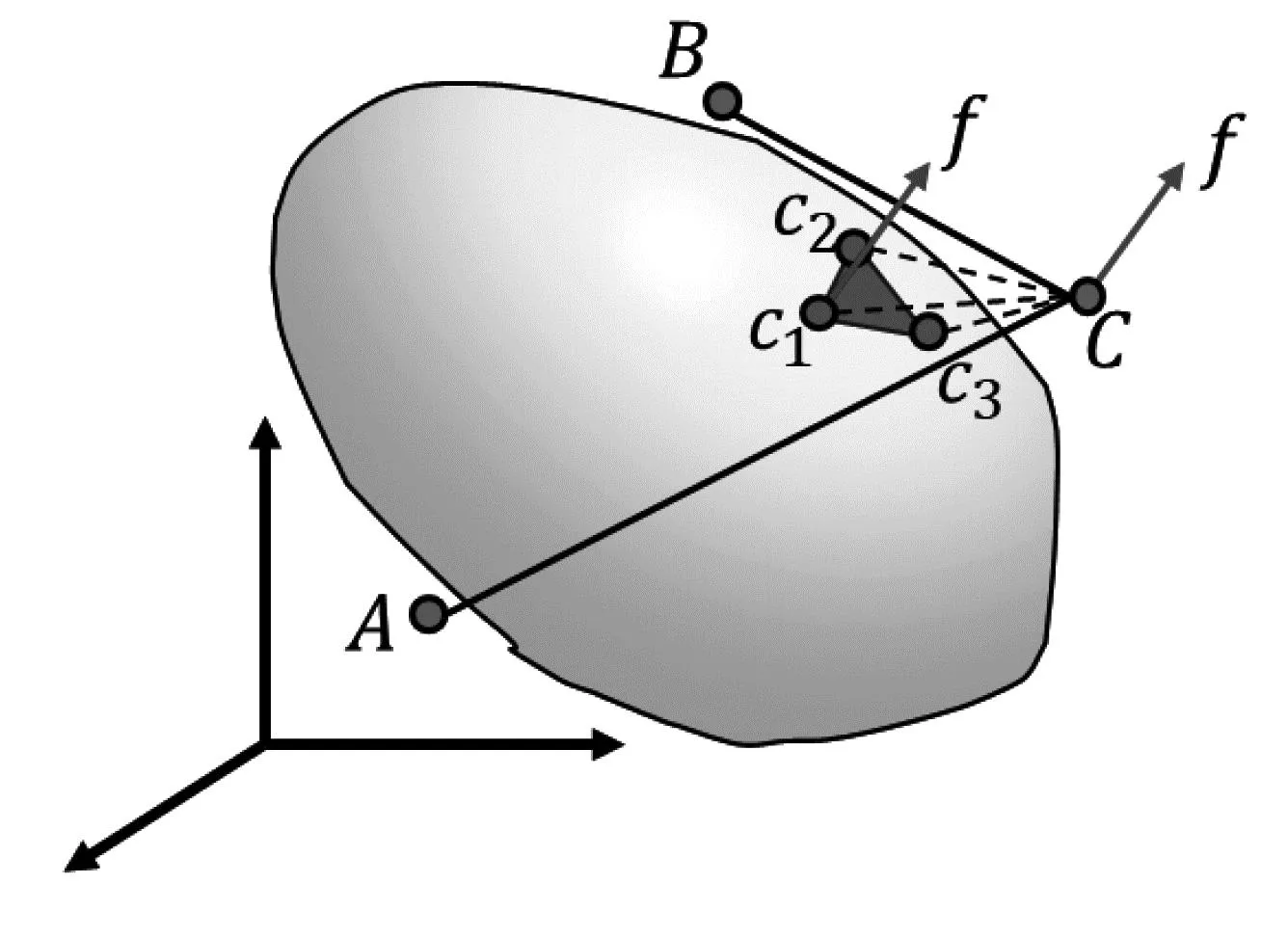
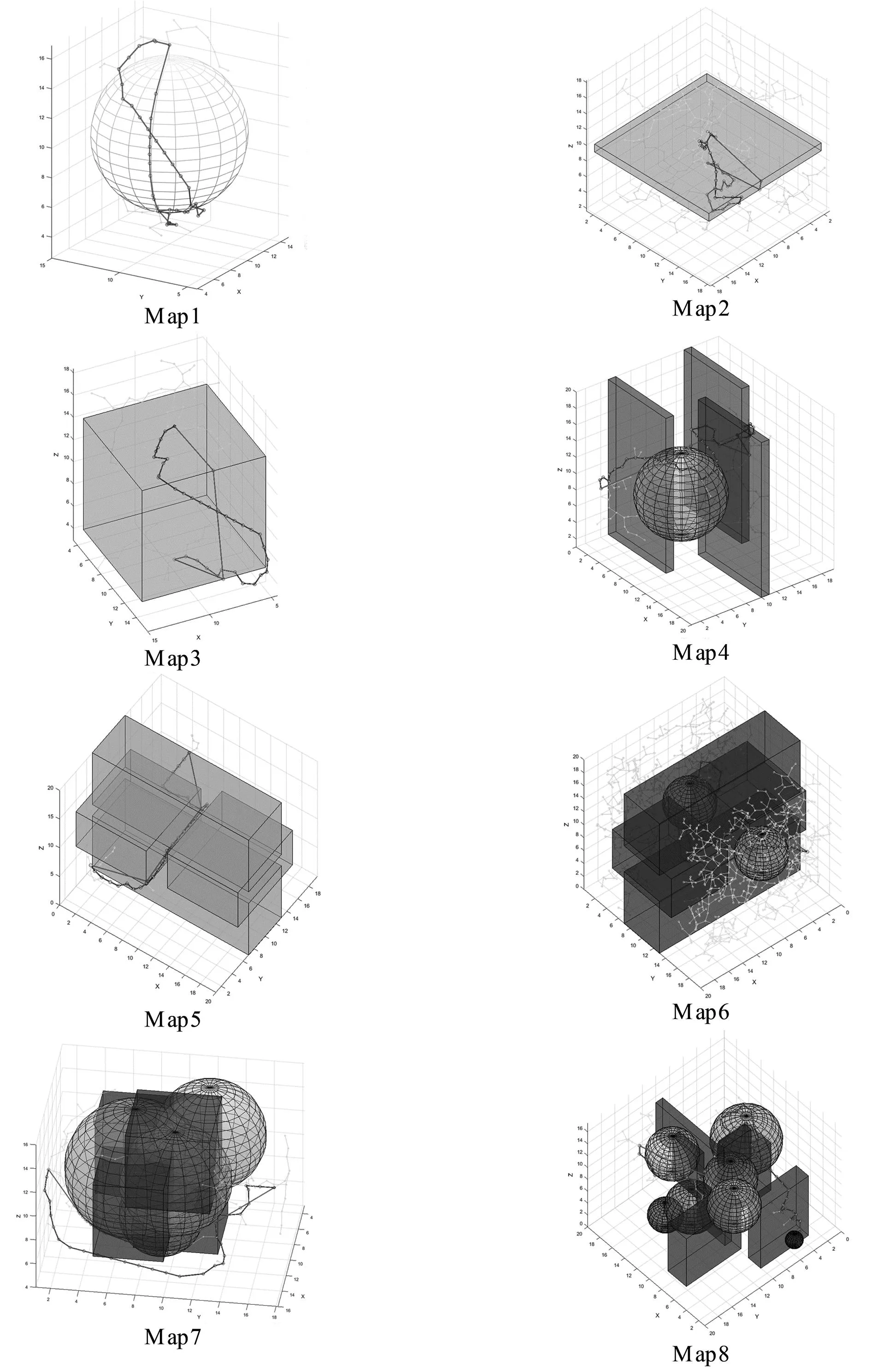
算法3的具体演示如图1所示。对于路径A-B-C,SRT算法先后构建出A-C,A1-C1,A2-C2三条潜在近路,A1和A2分别是A-B的1/2点和1/4点。SRT会依次对三条近路执行碰撞检测,如果某一条近路是无碰的,则直接连接该近路径。在图1中是A1-C1,显然Dist(A1-C1) 图1 SRT 算法演示 通常情况下,SRT的优化效果有限,空间中复杂的障碍会降低SRL的优化性能,导致SRT陷入局部极小值陷阱。SRL算法配合SRT算法组合成SRTL算法能有效地完成路径优化。SRL算法实现见算法 4。 在算法 4中,Line2代表对路径P中的每一个非端点进行遍历。Line3意味着对每一个非端节点执行MOVE操作,对节点尝试进行启发式位置扰动。Line4到Line10会对扰动后的节点和路径执行碰撞检测,如果是无碰的,则扰动成功,对路径的节点和边线进行更新。MOVE函数是SRL算法的核心,带来的扰动能帮助路径摆脱局部极小值陷阱,具体的算法实现见算法 5。 在算法5中,对于已经得到的路径P(V,E),∀xi∈V{xstart,xgoal},总是存在父节点xparent和子节点xchild。路径将被视作一条n维空间的绳子,vparent=xparent-xi和vchild=xchild-xi表征收缩时子节点和父节点对xi施加力的方向,其合力为vsum=vparent+vchild。如果Connectfree(xparent,xchild)为假且Connectfree(xparent,xi,xchild)为真,将xi沿着vsum方向移动,则∃δ∈R,使得Connectfree(xparent,xi+(δ+ε)vsum,xchild)为假且Connectfree(xparent,xi+δvsum,xchild)为真。我们定义同样的,如果对vsum施加微小的扰动得到由于公式2。 (2) 算法5的Line1到Line3用于 得到Vsum,Line4意味着在Vsum方向找到主锚点,也就是障碍物空间与非障碍物空间的交界面上的点。Line5和Line6表示对Vsum向量施加微小的扰动,从而得到更多的次锚点。依次将次锚点和主锚点连接后不难得到锚点向量空间C。 Line8意味着从Null(C) 空间中挑选扰动向量施加在Xi上使得Xi位置产生变化。如果扰动后的节点仍然使得路径无碰,则扰动成功,进而对路径的节点和边线进行更新。基于二分搜索实现的FIND函数实现请参考算法 6。 SRL算法的演示步骤如图2所示。在三维空间中存在的一个不规则障碍和一条无碰路径A-B-C。对于节点C来说,节点A和B分别是C的父节点与子节点。C1、C2和C3是C节点对应是三个锚点。三个锚点组成的局部区域在一定程度上描述了障碍物的局部区域特征。锚点区域的法向量f将会作用在节点上对其产生扰动。 图2 SRL算法演示 图3能演示了扰动带来的优化,在SRT算法很难在图3-1中继续对路径A-B-C进行优化。但是SRL算法对节点B施加扰动得到节点B1后,SRT算法能够进一步对路径进行优化得到更优的路径。在SRL和SRT算法的交替作用下,路径如同一根不断张弛的绳子,无碰路径将被优化为一条更短的路径。SRTL作为一种路径优化算法同样能与其他路径规划算法组合用于加速迭代优化的过程。 为直观展示SRTL算法的路径优化效果,构建了8张三维地图,如图4,其中包含了简单的单个障碍地图(Map1-3)、复杂的单个障碍环境(Map7)、稀疏多障碍环境(Map4)、稠密多障碍环境(Map8)和狭窄通道多障碍环境(Map5-6)等各类环境。我们测试了SRTL路径优算法在各类地图中路径优化的表现。 图4 Informed RRT*SR算法在三维空间的仿真结果 图4中的立方体和球体等物体代表障碍,蓝线代表RRT类算法生成的路径,红线代表经SRTL路径优化算法优化后的路径。图4表明由RRT类算法采样得到的蓝色路径点通常是蜿蜒曲折的,而优化后得到的红色路径往往更加便捷。实验表明,经路径优化算法优化后得到的路径将缩短15%左右。 RRT*-Smart同样是一种优秀的具备路径优化能力的路径规划算法,图5将Informed RRT*SR与RRT*-Smart算法进行对比。图5的球体是障碍物,蓝线是算法生成的中间结果路径,红线是对蓝线优化后的路径。实验表明,RRT*-Smart的智能采样和路径优化能力在高维空间中是有限的,其优化的结果受到了初始条件的影响,难以有效优化路径。Informed RRT*SR算法在空间中能得到一条更短的路径,图4和图5表明,由基于启发式扰动和二分采样的Informed RRT*SR算法得到的优化路径往往更加便捷。 图5 RRT*-Smart(左)与Informed RRT*SR(右)算法在三维空间的仿真结果 在Vrep中搭建了机械臂仿真环境为以进一步验证算法的有效性,利用Informed RRT*SR算法驱动六轴机械臂UR5中在障碍空间中成功进行了路径规划实验,结果如图6所示。图6表明,在相同的运行时间内,Informed RRT*SR能在六维空间搜寻得到一条更短的路径。 图6 Informed RRT*(左)与Informed RRT*SR(右)算法在机械臂路径规划仿真实验结果 在上述机械臂作业仿真环境中进行了上百次实验以对比测试算法的路径搜索能力。具体结果如图7与图8所示。 图7 Informed RRT*与Informed RRT*SR算法在近距离机械臂路径规划仿真实验结果 图8 Informed RRT*与Informed RRT*SR算法在远距离机械臂路径规划仿真实验结果 图7为近距离机械臂路径规划场景的结果,图8为远距离机械臂路径规划场景的结果。图中的每一个圆点的横纵坐标值代表每一次路径规划算法实验中找到的路径的时间与距离值。图中的曲线是基于样本点经LOESS算法拟合得到的结果,该曲线被认为是表征样本散点的一条局部平均值曲线。Informed RRT*SR算法的实验样本点与图7和图8的实验结果表明不论在近距离路径规划场景还是远距离路径规划场景,Informed RRT*SR算法都能在相同时间内找到一条更短的路径。Informed RRT*SR算法在近距离路径规划场景中对路径距离的优化率约为7%,而在远距离路径规划场景中对路径距离的优化率约为16%。 图9是依据实验结果绘制的算法时间与路径距离的直方图,图9-A是Informed RRT*算法的算法时间直方图,图9-B是Informed RRT*算法搜寻的路径距离直方图,图9-C是Informed RRT*SR算法的算法时间直方图,图9-B是Informed RRT*SR算法搜寻的路径距离直方图。图9-A和9-C表明,两类算法的运行时间分布大致相当,均呈现出“头部集中,尾部稀疏”的特点。图9-B和9-D表明,Informed RRT*SR算法搜寻的路径距离集中在头部附近,且整体分布优于Informed RRT*。 图9 Informed RRT*与Informed RRT*SR算法在机械臂路径规划仿真实验结果的算法时间与路径距离的直方图 在本文中,在Informed RRT*基础上提出了一种基于采样的路径规划算法Informed RRT*SR,通过指定启发式的探索和优化规则,Informed RRT*SR算法能更加高效地搜索得到一条便捷的无碰路径。本文提出的算法结合了基于采样算法的优点,能很好适应高维度空间的路径搜索问题。Informed RRT*SR算法中基于现有路径的优化方法能对状态空间进行更有针对性的探索。同时,Informed RRT*SR算法步骤中SRTL优化算法的模块化设计有助于工程师修改以适配不同的工业应用场景,这同样允许SRTL算法与其他基于采样的算法相互组合以更高效地解决路径规划问题。
1.4 路径松弛

2 仿真实验分析





3 总 结

