基于遗传算法的无线传感器网络路由优化

丁 凡,贺军义,陈素霞,黄全振

（1.河南理工大学 计算机科学与技术学院,河南 焦作 454003;2.河南工程学院 计算机学院,河南 郑州 451191;3.河南工程学院 电气信息工程学院,河南 郑州 451191）

无线传感器网络（wireless sensor network,WSN）[1]是由大批量小型智能传感器节点以自组织方式构成的无线网络。 相比于普通网络,WSN 以数据为中心,网络设置灵活,安全性和可靠性强且成本较低,在军事[2]、国防[3]、医疗[4]、农业[5]等领域具有重要的应用价值。 但在WSN 的实际应用中,由于节点采用电池供电,工作环境通常比较复杂,导致电池不能被充电或更换,所以整个网络的能量会受到影响。 因此,为保证网络生命周期最大化,必须从源节点到汇聚节点的诸多路由路径中找到一条节能高效的最优路由。

针对WSN 路由优化问题,国内外已有大量学者将一些智能优化算法应用于该领域,遗传算法就是其中的一种。 Rezaeipanah 等[6]以最大化网络生命周期为目的,从数据转发能耗和簇头节点数目选取出发,将遗传算法应用到WSN 簇间路由优化中,但其在适应度函数的构建中未考虑节点的剩余能量,若剩余能量较低的节点被选为路由节点,在迭代次数过多时将缩短网络生命周期。 陈立万等[7]将传统轮盘赌方法进行改进,结合交叉变异操作,筛选出具有最高适应度的个体作为最优路由路径,避免陷入局部最优,但算法中交叉变异操作均在值域范围内进行,产生的新个体并不能保证对应一条有效的路由路径。 Wang 等[8]提出了一种基于遗传算法的WSN 多路径路由算法,利用节点间的距离计算适应度函数,在基站生成与所有节点共享的路由方案,但该方案在生成路由路径时采用固定长度编码,使得寻找到的最优路径存在一定约束条件,最优路径可能不是全局最优。

由以上国内外文献可以看出,遗传算法与WSN 的结合虽存在一定缺陷,但也弥补了网络的一些问题。本研究在此基础上进行改进,依据遗传算法模型和WSN 的特点,将改进的遗传算法运用到WSN 路由优化中,采用可变长度染色体对路由路径编码,提前确定网络中各个节点的邻域节点,防止交叉、变异操作产生不符合条件的路径。 在形成路由路径时,考虑路径节点间距离、路径总能耗、节点剩余能量等因素,将遗传算法的快速全局寻优能力融入路由优化中,高效全面地搜寻目标路由路径。

1 WSN 路由模型

1.1 WSN 模型

在WSN 中,大量传感器节点随机分布在监测区域内周期性地感知周围信息,感知到的信息被融合筛选后经过多跳传输汇聚到汇聚节点（sink node） ,最终通过互联网到达终端用户。 假设WSN 模型如下:

1） 所有传感器节点都具有唯一的身份标识ID,编号为1,2,…,n。 网络中只含有一个汇聚节点,编号为n。

2） 网络中所有节点位置固定,各传感器节点初始能量相同,所有节点均可感知周围邻域节点的信息。

3） 节点的通信半径相同,当两个节点间的距离小于等于通信半径,即两节点互为邻域节点时,可直接进行通信。

4） 每个传感器节点的结构、功能相同,传输数据时节点可根据传输距离动态调整发射功率。

1.2 WSN 能耗

WSN 路由优化关键因素在于解决传感器节点能耗问题。 普通传感器节点主要由电源、感应单元、处理单元和无线通信单元4 个部分组成,如图1 所示。 收发单元是无线通信单元的一部分,主要负责信息转发,是网络中最大的能耗源。 收发单元存在空闲、接收、传输、休眠4种工作状态,空闲状态和休眠状态的能量消耗可以忽略不计,仅需要考虑节点在接收和传输状态的能量消耗。

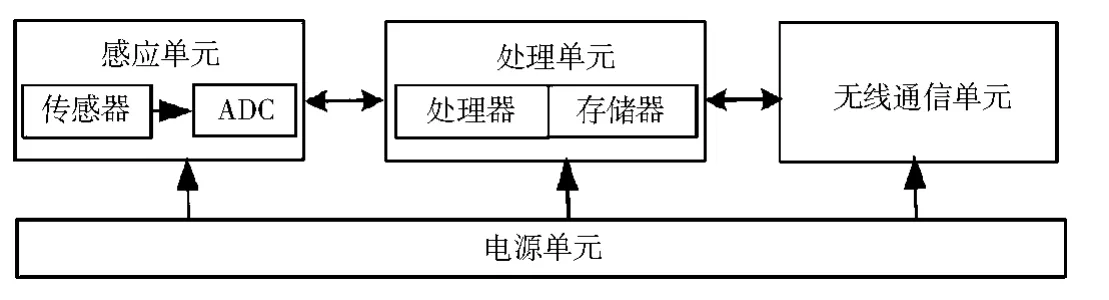
图1 传感器节点结构Fig.1 Sensor node structure

从一个节点发送kbit 数据到另一个节点,传感器节点所消耗的能量ET,以及接收kbit 数据传感器节点所消耗的能量ER分别为

此外,节点需要对接收到的数据进行融合处理,其能耗一般在数据传输时被消耗,故本研究不考虑该能耗。

1.3 WSN 路由优化模型

为找到更好的方法来降低网络整体的能量消耗,本研究将WSN 用带权无向图表示。 设图G=（V,E） ,其中V为WSN 的节点集,V=（v1,v2,…,vn） ,E为各传感器节点间的通信链路集,E=（e1,e2,…,em） ,d（vi,vj） 为节点vi到节点vj之间的距离,源节点到汇聚节点间可构建出多条数据传输路径χ,可表示为

式中:vi与vi+1为相邻节点;v1为源节点;vn为汇聚节点。 路径χ的总能量成本E（χ） , 即该路径上所有节点消耗的总能量成本,可表示为

路径χ的总长度D（χ） 为该路径上各个相邻节点间的距离总和,可表示为

WSN 路由优化的最终目标是寻找数据传输过程中从传感器节点到接收器节点高效节能的路由路径,若采用传统的穷举法从众多传输路径中选择一条最优路径,则会消耗大量的时间和资源。 本研究针对遗传算法能够解决大规模复杂优化问题的特性,将遗传算法运用到WSN 路由优化中,能更快、更准确地寻找最优路径。

2 基于遗传算法的WSN 路由优化

搭建完WSN 路由模型后,开始构建初始路由表,即生成遗传算法中的染色体,初始种群的构建需要考虑传感器节点间的通信距离。 在路由优化过程中,种群中的染色体需要经过多轮选择、交叉和变异,使其朝着符合WSN 路由优化的方向不断延伸和进化,从而找到最优路由路径。

2.1 编码

应用遗传算法解决实际问题时必须考虑编码问题,网络路由问题具有特殊性,路由路径有多条且长度可能不同。 因此,本研究采用可变长度编码方法,对网络中的每一个节点赋予唯一身份标识ID,个体用从源节点到汇聚节点之间经过节点的相应ID 序列表示。 在数据转发时,一个节点不能多次转发同一个数据包,故同一个体内不会出现重复节点。

2.2 适应度函数

种群中不同个体对环境的适应性不同,适应度函数就是判断个体适应性强弱的函数,适应度越高的个体对环境的适应性越强,越有可能被保留到下一代。 在遗传算法中,合适的适应度函数可加快算法收敛,保证算法的可行性。 由此可知,路由的优劣是用网络生命周期、传感器节点能耗、路由路径长度及其可靠性等因素来评估的,故为保证算法可行,在设计适应度函数时应考虑上述因素。

综上,适应度函数可表示为

式中:α、β、γ为路由路径长度与能量消耗间的权重系数;I（p） 为保证网络能量均衡消耗的参数,可防止能量较低的节点被选为路由节点,导致节点过早死亡而缩短网络生命周期。I（p） 计算公式如下:

由于路径短、能量消耗相对较少、节点负载均衡的路由路径为目标路径,故本研究要解决的最优化问题可转化为求解目标函数的最小值,需要对目标函数进行一定处理,将其映射为求最大值且函数值非负的形式,方法如下:

式中:fmax为当代种群个体中最大适应度;ξ为一个较小常数,可使种群中最差个体仍有继续繁殖的机会,增强种群多样性。 映射后的适应度函数应加大选择压力,增强择优功能。

2.3 种群选择

为避免算法过早陷入局部收敛,本研究在种群选择时采用最优个体保留策略[9]与轮盘赌算法[10]相结合的方法。 设种群大小为M,每轮选取N个适应度最高的最优个体直接保留到下一代种群中,剩余M-N个种群个体采用轮盘赌算法选择。 在轮盘赌算法中,个体被选中的概率与适应度成正比,即个体i被选中的概率如下:

2.4 交叉操作

交叉操作模拟自然界生物繁殖的特性,运用个体间的基因重组产生新的个体。 不同的交叉操作适用于不同的优化场景,常见的交叉操作有单点交叉[11]、多点交叉[12]、均匀交叉[13]及顺序交叉[14-15]等,本研究采取的方式为单点交叉。 传统单点交叉操作未考虑交叉位置前的节点与选择节点间是否存在链路,导致可能产生不符合条件的路由路径而影响网络运行,本研究对此进行了改进,使其能够有效地找到合适的路由路径。 交叉操作的具体方法如下:

1） 按照一定规则从种群中选取个体p1和p2,判断两个个体之间是否存在公共节点,若存在,则将公共节点后的基因片段进行交换重组。

2） 若不存在公共节点则随机选取交叉位置n1,判断p1中n1处的节点与p2中n1+ 1 处的节点是否能够组成链路,p2中n1处的节点与p1中n1+ 1 处的节点是否能够组成链路。

3） 若可以,则按照交叉概率判断是否交换两个染色体n1位置后的基因片段,否则不进行交叉。

在具体执行过程中,交叉概率过大可能破坏最优个体,过小可能导致算法收敛速度缓慢,故交叉概率应慎重设置。 同时,对于交叉后的个体应考虑是否存在重复基因,若存在,则将两个重复基因间的基因片段全部删除。

2.5 变异操作

变异操作可保持种群的多样性,防止遗传算法陷入早熟和局部收敛。 在进行变异操作时通常选取基因顺序交换变异和基因编号变异这两种方式,本研究采用基因编号变异。 具体操作过程如下:

1） 按照一定的规则从种群中选取个体p3,依据p3的编码长度随机选择除源节点与汇聚节点所在位置外的变异位置n2。

2） 观察n2前后位置节点的邻域,若两个邻域内存在重复节点,则依据变异概率决定是否将该节点作为变异节点来替换n2位置的节点,否则不进行变异。

变异操作后的个体同样可能存在重复基因,若存在,则依据上一小节的操作,将两个重复基因间的基因片段全部删除。

3 仿真实验与分析

3.1 仿真环境及参数设置

为验证本研究提出的算法对WSN 路由优化的效果,利用MATLAB R2016b 仿真软件搭建相应的仿真平台进行实验,仿真所用的具体参数如表1 所示。

表1 实验仿真参数Tab.1 Experimental simulation parameters

仿真环境中传感器节点将感知收集到的数据融合为大小相同的数据包,起始节点与汇聚节点的位置已经指定。 设定种群数量为20,主要探究从起始节点到汇聚节点多条路由路径中的最优路径。

3.2 适应度变化

本研究提出将遗传算法运用到WSN 路由优化中,经过多次仿真实验,得到前50 代种群平均适应度及最优个体的进化情况,如图2 所示。 由于遗传算法中存在交叉、变异等操作,每次得到的结果具有一定的随机性,故不同个体得到的适应度具有一定差异,但根据运行结果可以看出,种群内大部分个体的适应度接近最优结果。

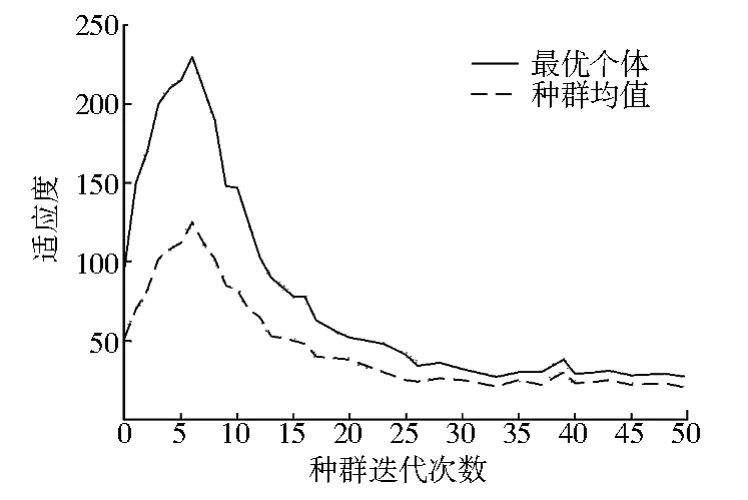
图2 适应度变化Fig.2 Change of fitness

由图2 可以看出,前6 次迭代内最优个体与种群均值的适应度均处于上升趋势且两者间的差值较大,此时种群内的个体多为随机生成个体;之后随着种群不断进化,适应度也不断下降,迭代到25 次左右变化趋势逐渐放缓,两条曲线的差值也逐渐减少;迭代45 次左右两条曲线基本收敛,表示已经形成最优路径。

3.3 网络最优路径

随机运行本研究提出的算法,得到的网络最优路径如图3 所示。 从图3 中可以看出,算法在指定起始节点处找到最优路径,该路径同时考虑节点间的距离及节点剩余能量,证明了该算法在WSN 路由优化中的应用具有高效性。

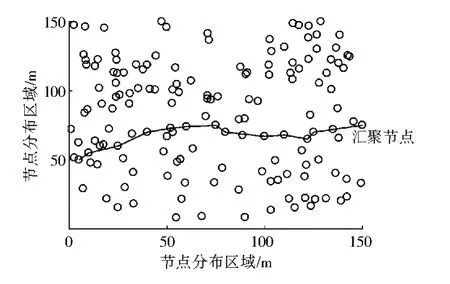
图3 仿真实验得到的最优路径Fig.3 Optimal path obtained from simulation experiment

3.4 网络能量消耗

Flooding 算法与本算法在数据传输过程中的能耗对比见图4。 从图4 可以看出,300 s 内,相较本算法,Flooding 算法的能量消耗上升斜率更陡,大约消耗了143 J 能量,而本算法大约消耗了46 J 能量,相比Flooding 算法下降了约68%。

图4 总消耗能量对比Fig.4 Comparison of total energy consumption

3.5 网络生命周期

本算法将网络生命周期定义为从开始运行到节点全部死亡经过的轮数,Flooding 算法与本算法在数据传输时的死亡节点数如图5 所示。 图5 中,Flooding算法在第90 轮就开始出现死亡节点,在第505 轮时节点全部死亡,而本算法在第503 轮才开始出现死亡节点,在第829 轮节点全部死亡。 就整个生命周期而言,本算法相比Flooding 算法提高了约64%,有效延长了网络生命周期。

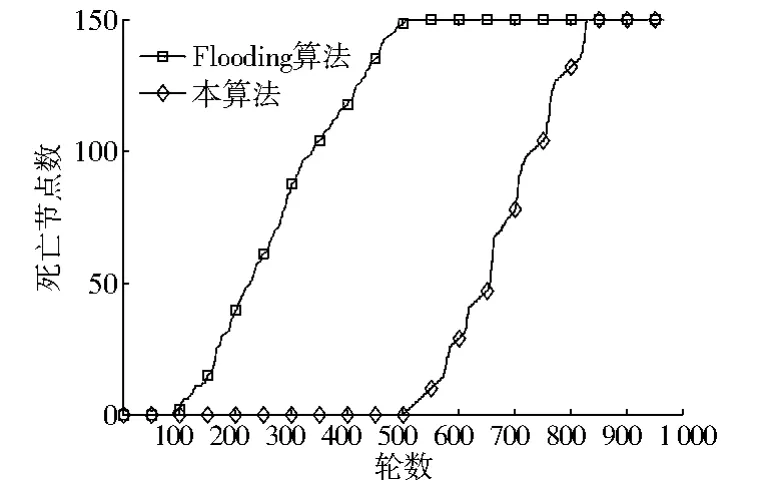
图5 死亡节点数对比Fig.5 Comparison of the number of dead nodes

4 结语

路由优化是保证WSN 寿命最大化的可靠途径。本研究在传统遗传算法的基础上,综合考虑多种约束条件,提出了一种基于遗传算法的WSN 路由优化算法。 该算法不仅考虑整个网络能量的均衡消耗,还根据路径规划及WSN 特点,设计了相应的遗传操作算子,保证经过多轮选择、交叉、变异后产生全局最优个体。 仿真结果表明,与Flooding 算法相比,本算法能有效减少能量损耗,延长网络生命周期。