次高斯复随机矩阵的算子范数估计

范俊辉,庄智涛

（华北水利水电大学 数学与统计学院,河南 郑州 450046）

随机矩阵最早由数学家Wishart 提出,是指元素为随机变量的矩阵,文献[1-3]介绍了有关随机矩阵的基础知识。 随机矩阵理论主要研究随机矩阵特征值（或奇异值） 的概率行为,其研究结果已经应用于许多领域,如计算数学、机器学习、优化理论等。 次高斯分布是应用中常见的一类重要分布,文献[4-6]介绍了次高斯和次指数实随机变量,并给出了一些实随机变量的集中不等式。 Vershynin[7]给出了次高斯实随机矩阵的算子范数估计。 上述研究都是在实空间中进行的,并未给出复空间中的情况,而在相位恢复[8-10]、Fourier 光学[11]等领域,复随机矩阵的应用更加广泛,因此研究次高斯复随机矩阵的算子范数估计具有重要意义。

本研究首先将实随机变量的性质推广到复随机变量,然后在此基础上给出次高斯和次指数复随机变量的集中不等式,最后利用ε-网技术对次高斯复随机矩阵的算子范数进行估计。

1 复随机变量的集中不等式

本节将给出次高斯和次指数复随机变量的定义,将次高斯和次指数实随机变量的性质推广到次高斯和次指数复随机变量上去,并在此基础上证明Bernstein 不等式和Hoeffding 不等式。 下面给出次高斯和次指数复随机变量的定义。

定义1一个复随机变量Z=X+ iY（X、Y都是实随机变量） 的次高斯范数为若Z的次高斯范数是有限的,则称它是次高斯的。

定义2一个复随机变量Z的次指数范数为若Z的次指数范数是有限的,则称它是次指数的。

文献[7] 介绍了次高斯和次指数实随机变量的性质:在R 中独立的次高斯随机变量X1,X2,…,Xn的和还是次高斯的,且一个随机变量X是次高斯的当且仅当X2是次指数的,且两个次高斯随机变量X、Y的乘积是次指数的,且下面的引理说明了复随机变量和它实部与虚部之间的关系。

引理1一个复随机变量Z是次高斯的当且仅当它的实部X和虚部Y都是次高斯的,并且有

引理2一个复随机变量Z是次指数的当且仅当它的实部X与虚部Y都是次指数的,并且有

证明假设Z是次指数随机变量,记所以有‖X‖ψ1≤a=‖Z‖ψ1,类似的有‖Y‖ψ1≤a=‖Z‖ψ1。 假设X、Y是次指

数随机变量,记‖X‖ψ1=a,‖Y‖ψ1=b,则有再利用不等式因为ex是一个凸函数,所以有

由定义2 可以得到‖Z‖ψ1≤a+b= ‖X‖ψ1+ ‖Y‖ψ1。

上面利用次高斯和次指数实随机变量的性质,证明了复随机变量的次高斯和次指数性与它的实部和虚部的次高斯和次指数性是等价的,接下来把这些性质应用到复随机变量上。

引理3设Z1,Z2,…,Zn为独立零均值的次高斯复随机变量,那么也是次高斯复随机变量,并且有其中C是一个绝对常数。

引理4一个复随机变量Z是次高斯的当且仅当Z2是次指数的,并且有设Z1、Z2是次高斯复随机变量,那么Z1Z2是次指数的,并且有

文献[7] 给出了次高斯和次指数实随机变量的集中不等式,设X1,X2,…,Xn为独立零均值的次高斯实随机变量,则存在绝对常数c,使得对任意t ＞0,都有

设X1,X2,…,Xn为独立零均值的次指数实随机变量,则存在绝对常数c,使得对任意的t ＞0,都有

在此基础上,证明复随机变量的集中不等式即Hoeffding 不等式和Bernstein 不等式。

定理1设Z1,Z2,…,Zn为独立零均值的次高斯复随机变量,则存在绝对常数c,使得对任意t ＞0,都有

证明令ξi=Xi（1 ≤i≤n） ,ξi=Yi（n+ 1 ≤i≤2n） ,将不等式两边同时取平方并代入ξi,可得

定理2设Z1,Z2,…,Zn为独立零均值次指数复随机变量,则存在绝对常数c,使得对任意t ＞0,都有

证明令ξi=Xi（1 ≤i≤n） ,ξi=Yi（n+ 1 ≤i≤2n） 。

最后,将ξi代入式（10） 并使用引理2 得到

2 复随机向量的性质

本节将讨论复随机向量的性质。 首先介绍各向同性随机向量的定义和性质,然后在次高斯实随机向量的基础上定义次高斯复随机向量并讨论其性质。 下面给出各向同性随机向量的定义。

定义3设Z是Cn中的随机向量,In表示单位矩阵,ZH表示Z的共轭转置。 若Z满足EZZH=In,则称它是各向同性的。

接下来给出各向同性随机向量的充分必要条件及其性质。

引理5Z是Cn中各向同性随机向量的充分必要条件,对于任意的z∈Cn都有

证明假设EZZH=In,等式两边同时左乘zH右乘z,可得假设因此,EZZH=In。

引理6设Z是Cn中各向同性随机向量,则有另外,如果Z和是Cn中两个独立的各向同性随机向量,则有

证明首先证明第一个性质。 因为看作1×1 的矩阵,所以由tr（ZHZ） =tr（ZZH） 和迹的线性性质,可得最后由各向同性的定义,可得接下来证明第二个性质。 首先固定,然后关于取条件期望,记作。 由全期望公式可得

前一节里已经介绍了次高斯复随机变量,现在把它推广到高维空间上去。 文献[7] 定义了次高斯实随机向量:一个实随机向量X∈Rn的次高斯范数在此基础上,定义次高斯复随机向量。

定义4一个复随机向量Z=X+ iY的次高斯范数为如果Z的实部X与虚部Y都是次高斯实随机向量,则称Z是一个次高斯复随机向量。

对于一个实随机向量X来说,如果对任意的x∈Rn,〈X,x〉 都是次高斯随机变量,则称X为次高斯实随机向量。 下面的定理3 表明这一性质对于复随机向量同样成立。

定理3一个复随机向量Z=X+iY是次高斯的当且仅当对任意的z∈Cn,〈Z,z〉都是次高斯随机变量。

证明首先证明充分性。 假设Z是次高斯复随机向量,则X、Y都是次高斯随机向量。 记z=a+ib,把内积展开得到

然后证明必要性。 假设〈Z,z〉 是次高斯随机变量,令zi=（0,0,…,1,0,…,0） ,可得Zi=Xi+iYi都是次高斯的。 因此,X、Y都是次高斯随机向量,由定义3 可知Z是次高斯复随机向量。

3 次高斯复随机矩阵的算子范数估计

本节将利用ε-网技术,给出次高斯复随机矩阵的算子范数估计。 首先介绍ε-网。 设（T,d） 是一个度量空间,K是T的一个子集,ε ＞0,如果对任意的x∈K都存在x0∈N使得d（x,x0） ≤ε,则称N是K的一个ε-网。 若N是K的所有ε-网中元素数目最小的集合,则称N的元素数目是K的覆盖数,记作N（K,d,ε） 。如果度量空间（T,d） 的子集N中所有不同的点x、y都有d（x,y）＞ε,则称N是ε-分离的。 集合K⊂T的ε-分离子集的最大可能数目称为K的填充数,记作P（K,d,ε） 。 特别地,若N是K的一个极大ε-分离子集,那么N是K的一个ε-网。 并且,对于任何集合K⊂T和任意ε ＞0,都有P（K,d,2ε） ≤N（K,d,ε） ≤P（K,d,ε） 。 设A和B是度量空间（T,d） 的子集,记A+B∶={a+b∶a∈A,b∈B}。 下面的引理说明了覆盖数和度量空间中体积的关系。

引理7[7]设K是度量空间（T,d） 的一个子集,则对于任意的ε ＞0,都有

因为Cn同构于R2n,所以很容易得到复单位球的覆盖数与维数n呈指数关系。

引理8对于任意ε ＞0,Cn中的单位球Bn2的覆盖数满足

接下来将利用ε-网计算一个矩阵的算子范数。

引理9[7]设A是一个m×n复矩阵,ε∈[0,1） 。 令N是Sn-1上任意一个ε-网,则

因为矩阵的算子范数除由向量的范数导出外,还可以由向量的内积导出,所以可以在ε-网上用向量的内积导出矩阵的算子范数。

引理10设A是一个m×n（m≫n） 复矩阵,ε∈[0,1/2） ,令N、M分别是Sn-1和Sm-1上任意一个ε-网,则有

如果m=n,且A是Hermitian 矩阵,则有

证明首先证明式（17） 。 因为接下来证明上界,首先固定两个向量x∈Sn-1,y∈Sm-1满足然后选择x0∈N,y0∈M,使得利用内积的性质和三角不等式, 可得

文献[7] 给出了带有独立次高斯元素的实随机矩阵算子范数的集中不等式,现将这个结论应用到复随机矩阵上,给出复随机矩阵算子范数的一个上界估计。

定理4设A是一个m×n复随机矩阵,它的每一个元素Ai,j都是独立零均值的次高斯复随机变量,则对于任意的t ＞0,都有成立的概率至少为1- 2exp（-t2） 。 其中,C是一个较大的绝对常数。

证明令N、M分别是Sn-1和Sm-1的1/4-网。 由引理8,可得由引理10,矩阵A的算子范数可以利用ε-网来控制:

然后,固定x∈N,y∈M,则是独立的次高斯复随机变量的和。 由引理3,可得将它表示成概率的形式,即对任意的u ＞0,有

接下来,对任意的x、y,估计它们的一致上界。 假设事件发生,那么就存在x∈N,成立,因此

令C≥ln 18/c1,可得

下面将改进定理4 的结果。 首先,给出复随机矩阵更加精确的双侧界。 然后,将复随机矩阵每个元素是独立的放宽到每个行向量是独立的。

定理5设A是一个m×n复随机矩阵,它的每一行Ai是Cn中各向同性独立零均值的次高斯复随机向量,则对于任意t ＞0,都有成立的概率至少为1- 2exp（-t2） 。 其中,δ=C是一个较大的绝对常数。

证明首先令N是Sn-1上的1/4-网,则由引理10,可得然后,固定x∈N并将表示为随机变量和的形式,即由于Ai是各向同性独立的次高斯随机向量且是次高斯随机变量且从而有X2i- 1 是独立零均值的次指数随机变量。 由引理4,可以得到现在使用推论3,对任意的ε ＞0,都有令ε=CK2max（δ,δ2） 且C≥1,则将δ代入并利用不等式（a+b）2≥a2+b2（a≥0,b≥0） ,可得接下来,对任意的x估计它们的一致上界。 假设事件发生,那么就存在x∈N使得成立,因此

令C≥ln 18/c1,可得

令si（A） 是矩阵Am×n（m≫n） 的奇异值,并按非递增顺序（s1（A） ≥…≥sn（A） ≥0） 排列。 接下来,给出随机矩阵A的全部谱（奇异值） 的一个双侧界估计。

推论1设A是一个m×n（m≫n） 复随机矩阵,它的每一行Ai是Cn中各向同性独立零均值的次高斯随机向量,则对于任意t ＞0,都有成立的概率至少为1- 2exp（-t2） 。 其中是满足定理5 的绝对常数且CK2≥1。

证明由定理5 可知因为由于CK2≥1,所以1+CK2max（δ,δ2） ≤1+CK2（2δ,δ2） ≤1+2CK2δ+（CK2δ）2=（1+CK2δ）2。 因此,s2i（A） ≤m（1+CK2δ）2,将δ代入可以得到si（A）若CK2max（δ,δ2） ≥1,下界显然成立。 若CK2max（δ,δ2）＜1,则有1-CK2max（δ,δ2） ≥1-CK2δ≥1- 2CK2δ+（CK2δ）2= （1-CK2δ）2。 因此,s2i（A） ≥m（1-CK2δ）2,将δ代入可得si（A）

4 数值实验

本节通过数值算例展示定理5 和推论1 的有效性。 在数值实验中,使用复高斯随机矩阵A∈Cm×n,其中随机矩阵的每个元素都是独立同分布的标准复高斯随机变量,即ak,l～N（0,1/2） +iN（0,1/2） 。 取t从0.1到3.0,步长为0.1。 对于每个t,做1 000 次实验,从而得到实验的经验概率。

算例1验证定理5 的准确性。 在实验中,分别选择n= 50,m= 500 和n= 50,m= 1 000。 令C= 3.9,对于每个t,当算子范数满足定理5 的不等式时,记实验有效次数加1,并称实验有效次数与1 000 的比值为定理5 的不等式成立的经验概率Pt。

图1 展示了算例1 理论概率下界1- 2exp（-t2） （虚线） 与经验概率Pt（实线） 在[0,3.0] 上的值,结果显示理论概率下界是一个良好的估计。

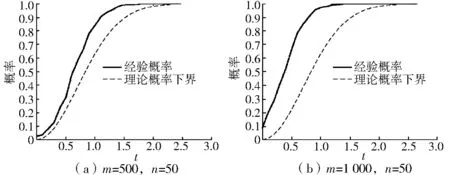
图1 算例1Fig.1 Example 1

算例2验证推论1 的有效性。 同样考虑n= 50,m= 500 和n= 50,m= 1 000 两种情况。 令C= 1.8,当随机矩阵A的奇异值满足推论1 的不等式时,记实验有效次数加1,并称实验有效次数与1 000的比值为推论1 不等式成立的经验概率Pt。

图2 展示了算例2 理论概率下界1- 2exp（-t2） （虚线） 与经验概率Pt（实线） 在[0,3.0] 上的值,结果显示理论概率下界是一个良好的估计。

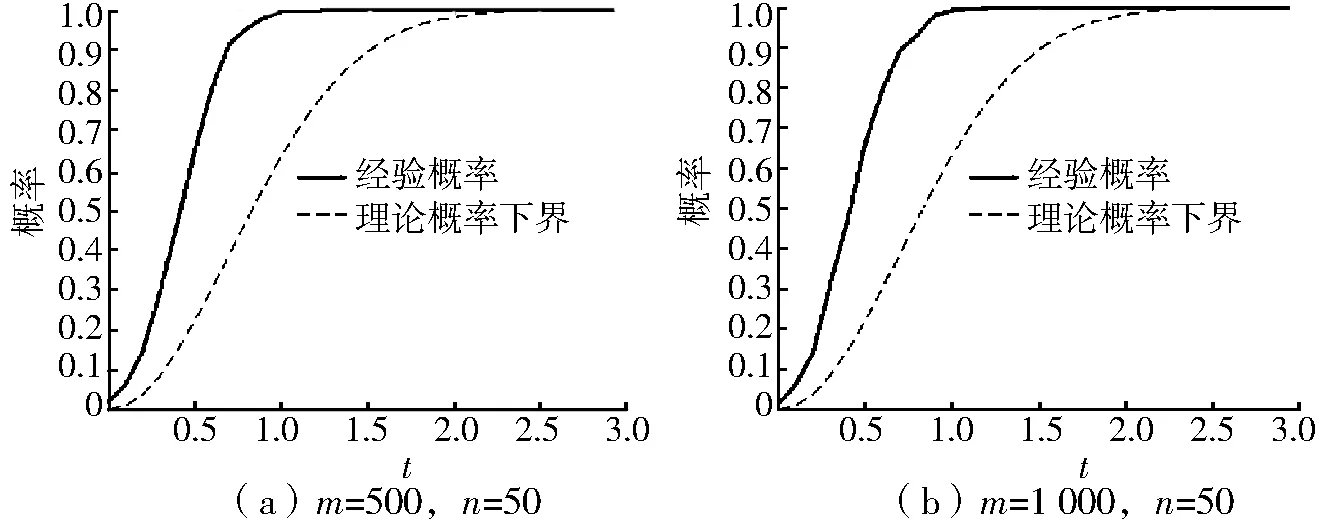
图2 算例2Fig.2 Example 2

5 结语

本研究将实空间中的次高斯和次指数分布的性质应用到复空间中,并利用这些性质证明了复随机变量的Hoeffding 不等式和Bernstein 不等式。 此外,利用ε-网技术给出了次高斯复随机矩阵算子范数的一个双侧界估计。