基于数值模拟的新型无反馈射流振荡元件性能影响因素研究

杨 庆

(东北师范大学环境学院)

引 言

浮选作为常见选矿方法,被广泛应用于处理贱金属、稀有金属及贵金属矿石。然而,该方法只有在处理粒度为30～70 mm矿物时,才能从原料中有效回收有价矿物,大量粒度远小于20 mm矿物中有价值成分损失在选矿尾矿中。考虑到富矿枯竭和开发细粒级矿物的需要,亟须研发高效的细粒级矿物浮选方法[1-4]。针对细粒级矿物浮选的关键问题,国内外开展了大量的基础研究,主体思路之一是:根据颗粒与气泡的匹配性原理减小气泡尺寸,从而改善微细粒浮选效果[5]。然而,如何以廉价且有效的方式产生微泡仍然是个难题[6]。

近年来,在气泡生成方面的研究进展表明:微泡可以经由振荡射流通过起泡装置产生,振荡射流是由稳定气流通过一个射流振荡器转换而来的[7]。ZIMMERMAN等[8]研究发现,利用附壁式流体振荡器脉动进气的方法能够产生高能效、大小为20～100 μm的微泡。调查发现,振荡射流进气方式没有额外能量的输入,并且射流振荡元件无自由移动部件,具备功率小、价格优廉、能适应极端环境、寿命长等优势[9]。

无反馈射流振荡元件是近年新兴起的一种无反馈结构的流控元件,在具有附壁式射流振荡元件特点的同时,结构也更加简单[10]。查阅文献发现,国内外学者仅对无反馈射流振荡元件基础构型的振荡机理、内部流场等进行了大量模拟研究,而元件优化设计和工程应用的研究相对较少[11-14]。因此,研究尝试在无反馈射流振荡元件基础构型上增加分流劈,并对其不断优化,将由圆腔出口无规则喷射而出的射流变为周期性、以正负交替方式切换方向产生的脉冲流;随后根据分流劈模拟结果,确定形成稳定振荡的最佳参数组合,结合文献中模拟优化所得无反馈射流振荡元件基础构型的几何参数,加工出新型无反馈射流振荡元件,进而应用于去除金矿中二氧化硅浮选试验。

1 模型构建

1.1 物理模型

在无反馈射流振荡元件基础构型的基础上,使用机械设计软件SolidWorks对新型无反馈射流元件进行三维建模。为了保证计算的准确性及模型更好的收敛,确保出口边界条件可以正确设置,分流劈2个出口处增加了矩形计算域。无反馈射流振荡元件基础构型见图1,新型无反馈射流元件的二维及三维图见图2。

图1 无反馈射流振荡元件基础构型示意图

图2 新型无反馈射流元件物理模型

本文针对新型无反馈射流振荡元件的分流劈进行模拟优化设计,分流劈几何尺寸见图3。分流劈形状为凹型,除此之外还有尖锐型与凸型,见图4。

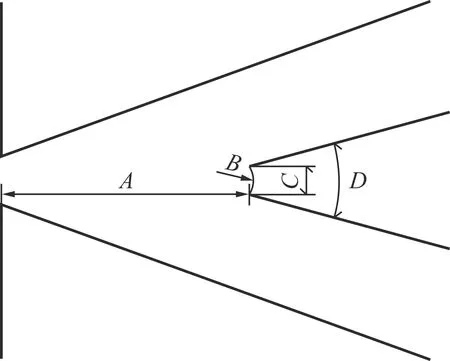
A—分流劈距离 B—分流劈半径 C—出口管间距离 D—分流劈角度图3 分流劈几何尺寸示意图

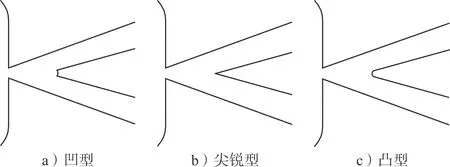
图4 各类型分流劈形状示意图

1.2 控制方程

该研究的工作流体为空气,气流速度较大且具有压缩性、黏性。另外,流体流动遵循流体力学中质量守恒定律、能量守恒定律与动量守恒定律。因此建立控制方程[15]。

1)连续方程(Continuity Equation):

(1)

式中:ρ为射流自身密度(kg/m);t为时间(s);u、v为速度矢量在x、y方向上的分量(m/s)。

2)动量方程(Navier-Stokes Equation)

(2)

(3)

式中:μ为动力黏度(Pa·s);Su、Sv为动量守恒方程的广义源项。

3)能量方程(Energy Equation):

(4)

式中:T为温度(K);Cp为比热容(J/(kg·K));k为流体的传热系数;ST为流体的内热源及由于黏性作用流体机械能转换为热能的部分,简称为黏性耗散项。

4)理想气体状态方程(Ideal Gas Equation):

p=ρRT

(5)

式中:p为气体压强(Pa);R为摩尔气体常数(m2/(s2·K-1))。

在上述控制方程组中,有5个未知函数、5个方程,方程组封闭,可以应用ANSYS CFX19.2软件求解和流体流动有关的物理量。

1.3 湍流模型

本文研究对象为新型无反馈射流振荡元件,工作时其内部空气处于高流速、非稳定状态,因此在数值模拟过程中,选择合适的湍流模型至关重要。对方程的直接数值模拟(DNS)由于计算量过大,目前在工程中使用较少。工程中常用基于雷诺时均法的湍流模型(RANS)及介于DNS与RANS之间的大涡模拟(LES),LES计算量较大,一般用于分析噪声问题等。该研究采用RANS方法来进行计算。

k-ωSST湍流模型是目前计算精度较高的一种RANS模型,解决了湍流剪切应力输运问题,可以较好捕捉壁面吸附分离等现象,适用于本研究的计算。

1.4 边界条件与求解设置

采用瞬态计算法,总计算时长设为3 s,时间步长设定为0.000 5 s,每10步记录一次;温度设定为30 ℃,壁面均采用绝热无滑移边界;采用流速入口、压力出口的边界条件,流速设定为20 L/min,压力设定为10 000 Pa;采用精度高、收敛好的有限体积离散方法进行数值计算。在分流劈出口管与出口堰交界处设置2个监测点。

1.5 网格划分与无关性检验

1.5.1 网格划分

网格划分与生成前需要选择网格形状与存储方式。由于研究的几何模型不算复杂,为了提高精度、节省计算资源及时间,本文选择六面体结构网格转非结构网格的方式来离散计算域。模型整体网格划分见图5-a)。

图5 新型无反馈射流振荡元件网格划分

提高网格质量的方式之一是对整体网格加密,但要注意,网格加密虽然可以适当提高计算精度,但网格密度过大需要占用更多的计算资源,可能造成非物理解。因此,先对整体网格加密,再根据流场需要进行局部加密,还需要注意在局部加密处与相邻处有一定的过渡,否则网格梯度过大也会导致非物理解。在振荡腔、圆腔内部处,由于流体碰撞激烈且流动较为敏感,需进行局部加密,其余区域采用均匀网格。局部网格加密情况见图5-b)。

1.5.2 网格无关性检验

研究划分了5种不同密度的网格,其数量梯度从38×104增加到97×104,选取2个出口管末端与矩形计算域连接处为监测点。5种不同网格数量下的监测点频率变化见图6。由图6可知:频率变化并不显著,因此可以认为仿真模拟受网格数量的影响不大。考虑到计算资源与收敛效果,选择50×104网格数量进行求解计算。

图6 网格无关性检验

2 模拟结果

就元件几何尺寸对振荡性能的影响进行了分析,以出口频率作为衡量指标,研究了不同几何参数对振荡器频率的影响。可以产生振荡的具体参数设置见表1。

表1 振荡器设计几何参数

2.1 分流劈距离

振荡腔为分流劈、圆腔出口及周围壁面的夹带区,对主射流的附壁距离、振荡性能及压降等均有重要的影响,分流劈距离对新型无反馈射流振荡元件振荡性能的影响见图7。由图7可知:随着分流劈距离从3.7 mm增加至4.5 mm,频率由13.03 Hz增加至32.00 Hz;随后继续增加分流劈距离至4.6 mm,频率反而减小至29.74 Hz,减少幅度约为7 %;且在分流劈距离小于3.7 mm或大于4.6 mm时不会产生振荡。说明适当增加分流劈距离有利于提高元件的振荡性能和双稳特性,即易于振荡;但随着分流劈距离持续增加,会影响到立涡形成时间和发展,进而减少射流的切换,且分流劈距离过大会导致振荡腔面积显著增加,同时由于射流卷吸作用会造成能量耗散,表现为振荡周期变长、频率值变低。因此,在特定工况下,确定分流劈的合理位置是非常重要的。

图7 分流劈距离对新型无反馈射流振荡元件振荡性能的影响

2.2 分流劈半径

分流劈半径对新型无反馈射流振荡元件振荡性能的影响见图8。由图8可知:分流劈半径由0.4 mm增加至0.5 mm后,频率由22.47 Hz增加至27.39 Hz,增幅约21.90 %。说明适当增加分流劈半径可使射流双稳特性得到较好的保证,且易于振荡;但随着分流劈半径继续增大直至0.9 mm,频率呈衰减趋势,最终下降至21.16 Hz。考虑是射流附壁过程中由于卷吸作用从非附壁侧进入振荡器的气体更多,造成能量损失增大,同时出口压力恢复变慢,表现为频率减小。

图8 分流劈半径对新型无反馈射流元件振荡性能的影响

2.3 分流劈角度

分流劈角度简称劈角,也称为出口管角度,指分流劈处两侧壁的夹角。分流劈角度对新型无反馈射流振荡元件振荡性能的影响见图9。由图9 可知:随着分流劈角度增加,频率先呈线性增长,由28°时的21.56 Hz增加至30°时的27.39 Hz,并达到最大值;之后分流劈角度与频率呈负相关,频率随着分流劈角度的增加而下降,最终降至33°时的25.48 Hz。射流和侧壁的碰撞区域是强湍流区,该区域需要耗散能量,而分流劈角度又会对碰撞区域湍流耗散的大小造成影响,进而影响射流总压损失。

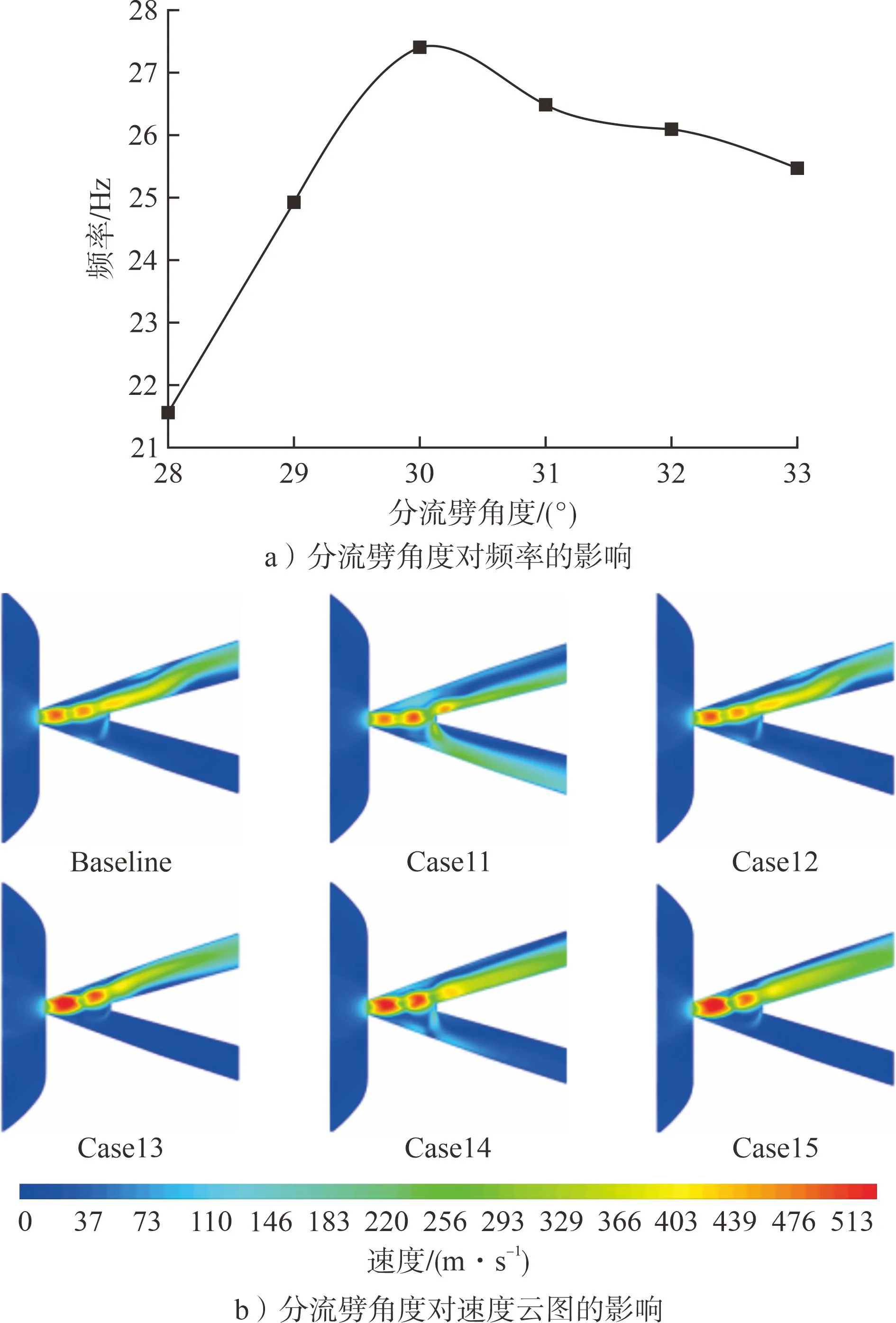
图9 分流劈角度对新型无反馈射流振荡元件振荡性能的影响

2.4 出口管间距离

出口管间距离对新型无反馈射流振荡元件振荡性能的影响见图10。由图10 可知:当出口管间距离由0.3 mm增加至0.4 mm后,频率由24.81 Hz增加至31.91 Hz,增长了28.62 %;继续增加出口管间距离,频率开始持续降低,直至降低至0.7 mm时的18.73 Hz。说明适当增加出口管间距离会使频率增加,即易于振荡;继续增加出口管间距离,振荡腔面积相应增加,造成主射流在射气过程中卷吸的气体量增加,导致压力损失增大,表现为频率降低。

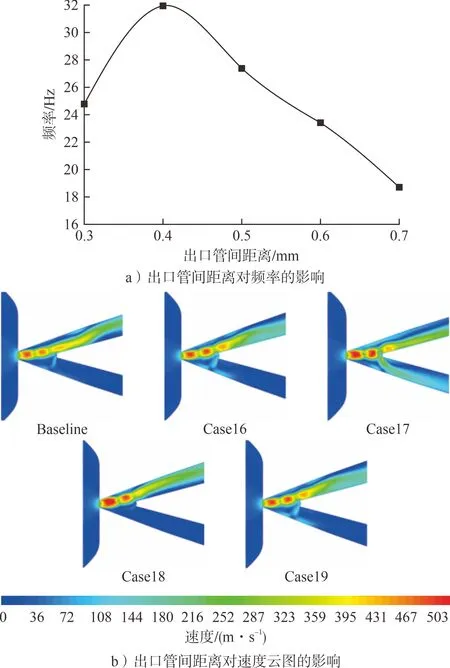
图10 出口管间距离对新型无反馈射流振荡元件振荡性能的影响

2.5 分流劈形状

分流劈形状对新型无反馈射流振荡元件振荡性能的影响见图11。由图11可知:不同分流劈构型下频率表现出差异,凸型下的34.43 Hz相较于尖锐型下的31.45 Hz与凹型下的27.39 Hz有一些提升。这是因为凸型结构减少了振荡腔的面积,致使射入的主射流气体量减少,射流卷吸周边流体量也减少,从而减少了能量损失。尖锐型分流劈的尖锐部分虽会造成能量损失,但振荡腔面积仍小于凹劈。

图11 分流劈形状对新型无反馈射流振荡元件振荡性能的影响

3 新型无反馈射流振荡元件去除金矿石中二氧化硅浮选试验

结合文献中模拟优化所得无反馈射流振荡元件基础构型的几何参数,并在上述分流劈模拟优化结果的基础上,加工并组装新型无反馈射流振荡元件。选取某二氧化硅品位为79.3 %的金矿石,进行浮选试验,对比研究使用及不使用新型无反馈射流振荡元件浮选二氧化硅去除率。

3.1 试验材料

某二氧化硅品位为79.3 %的金矿石;醚胺、3-(2-乙基己氧基)丙胺分别用作捕收剂和起泡剂,并且使用乙酸中和水溶液中醚胺以增加其溶解度;试验用水均为当地自来水。

3.2 试验设备

浮选试验设备形象联系图见图12。浮选装置包括带有筛网分布器(孔径为105 μm)的柱(直径6 cm,高150 cm)。将供液泵放在起泡器上方100 cm处的柱旁,并以一定的流速将柱底的排放物由排液泵流出,以控制矿浆-泡沫界面。微气泡发生系统进气方向由右至左,使用新型无反馈射流振荡元件将空气供应模式由稳定变为振荡,通过由稳压器与流量计组成的供气控制装置调节。为了进行比较,将虚线内装置去除则为正常气泡发生系统。

图12 浮选试验设备形象联系图

3.3 试验结果

试验结果显示,对于小于10 μm的细粒二氧化硅,不使用新型无反馈射流振荡元件稳定进气时,浮选回收率为28.9 %;当使用新型无反馈射流振荡元件进行振荡进气时,浮选回收率提高至42.2 %,增幅为46 %,大大提高了浮选回收率。

4 结 论

针对新型无反馈射流振荡元件进行了三维模拟,得出了射流的振荡频率随分流劈结构参数的变化规律,并且给出了详细合理的描述,主要结论如下所示:

1)考察的分流劈参数包括分流劈距离、分流劈半径、分流劈角度、出口管间角度、分流劈形状,它们对振荡频率都有一定的影响。分流劈距离增加,振荡腔容积也随之增大,频率呈先增加后减小趋势,3.7 mm处为最小值13.03 Hz,并在4.5 mm处达到最大值32.00 Hz。此外,在模拟数值的上下限继续增加或者减少分流劈距离将无明显振荡。将分流劈半径自0.4 mm增加至0.9 mm,频率呈现先增大再减小的趋势,但是变化并不显著。增加出口管间距离,振荡区的面积也会增大,使得主射流在射气过程中卷吸的气体量增加,引发压力损失增大,这是出口频率降低的原因。分流劈角度的模拟优化结果表明,最高频率为30°时的27.39 Hz,最低频率为28°时的21.56 Hz,最大变化幅度约为27.04 %。对于不同的分流劈形状研究表明,在相同分流劈距离下,凸型构型频率更高,即振荡效果更好。

2)在去除金矿石中二氧化硅浮选试验中发现,通过使用新型无反馈射流振荡元件将空气供应流动模式从稳定转换为振荡,二氧化硅细粒级浮选回收率显著提高,增幅为46 %。