基于APOS理论的概念教学设计

孙丹丹

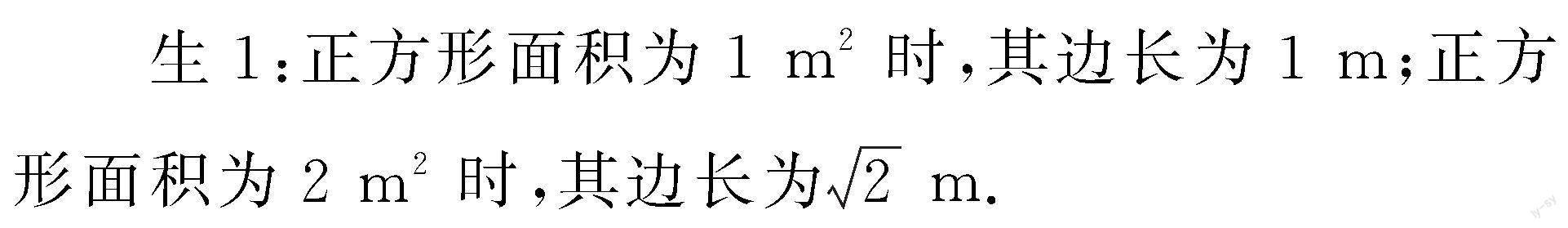
摘要：数学具有抽象概括性，因此数学教学要遵循这一特点；APOS理论基于数学抽象性的特点，将数学概念的学习概括为操作或活动、过程、对象、概型四个阶段.本文中以初中数学“实数”的教学为例，得到基于APOS理论为框架数学概念教学的教学设计.

关键词：初中数学；实数教学；APOS理论

数学概念是解决数学问题的基础，因此概念教学是初中数学教学的重点和难点.但是，目前初中生还不能深入理解某些数学概念，基于此运用APOS理论模型通过具体实例，帮助学生初步理解数学概念，让学生在此基础上进行思维内化，抽象出数学概念的本质属性，再将其精确化为具体的数学对象，最后形成关于该数学概念的综合心理图式[1].APOS理论给出了数学概念教学的具体步骤，为初中数学概念教学提供了理论基础，降低了初中数学概念教学的难度.

1 教学设计

1.1 操作或活动阶段：实例直观，激发兴趣

问题1 为了美化校园，学校打算建一些正方形花坛，如果每个花坛面积为1 m2，那么正方形的边长应为多少？如果把每个正方形的面积改为2 m2，此时应该怎样确定正方形的边长？

设计意图：从学生生活中的实例出发，使学生感受到数学在生活中的作用，问题设计层层深入，激发学生的探究兴趣.

1.2 过程阶段：思维内化，抽象概念

环小数，并给出“无限不循环小数又叫做无理数”的定义.

1.3 对象阶段：合作探究，领悟概念

问题3 你能列举出一些无理数吗？

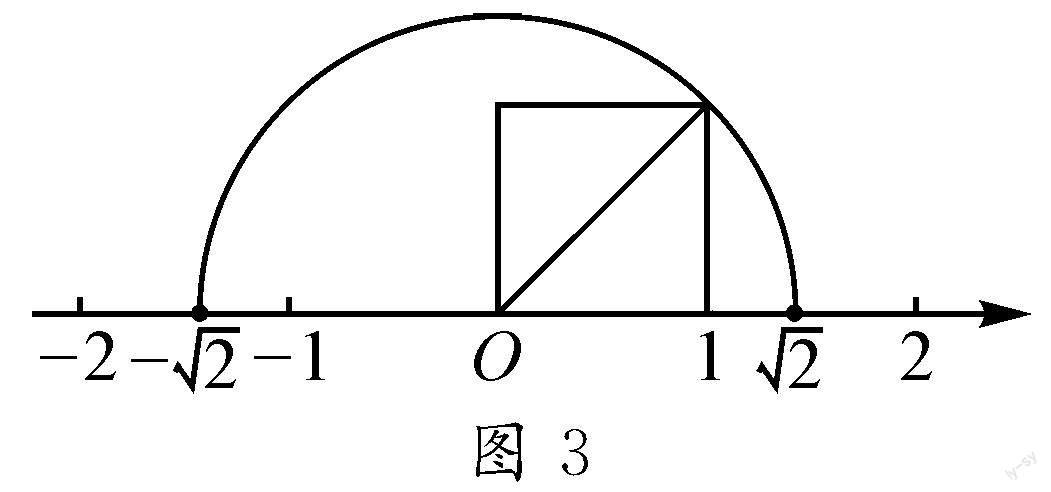
如图2，将直径为1的圆从原点O出发沿着数轴正方向滚动一周，O′的位置对应的数就是π.

来吗？

在学生深刻理解無理数的概念后，教师给出实数的概念，即有理数和无理数统称为实数.

问题6 类比有理数m与其相反数和绝对值的关系，你能总结归纳出实数t与-t和|t|的关系吗？

小组合作探讨，得到：

问题7 数轴上的点和实数之间有什么关系？

学生4：一一对应关系.

设计意图：类比有理数与数轴上点的对应关系，总结出无理数与数轴上点的对应关系，体会数形结合思想，为学生理解高中数学中集合的概念作铺垫.

1.4 概型阶段：建立联系，综合概念

问题8 实数由哪些数组成？你能分类吗？

问题9 还有其他分类方式吗？

设计意图：把新知识实数、无理数与已学的知识建立联系，让学生形成关于实数的综合心理图式.同时，将零散的知识系统化则有助于学生记忆该概念，并能够有效地加以运用.

2 教学反思

2.1 注重实例直观，激发学习兴趣

数学源于生活，生活中的实例能使学生更容易理解题目，激发探究热情.通过实例直观，从具体到抽象帮助学生理解数学概念.同时，在问题探究的过程中培养学生的数学建模能力.在基于APOS理论的“实数”的教学中，从学校修建花坛的实例出发，让学生体会发生在身边的数学问题，通过利用数学知识解决现实问题，感悟数学的魅力;用计算器计算2，让学生亲眼看见运算过程，记忆深刻;用PPT动态演示“π”的形成过程，使学生看到“思维的过程”，加深学生对实数与数轴上的点一一对应关系的理解.但教学过程中要避免“为了直观而直观”的现象，要注重实例直观的真实可靠性.

2.2 重视动手操作，培养数学抽象能力

2.3 提倡合作交流，提升数学抽象能力

基于APOS理论的“实数”教学中，“过程”和“对象”阶段都需要学生有较强的数学抽象能力，所以通过小组合作探究，组内成员相互启发引导，有助于学生更好地抽象和理解数学概念.在学生“抽象概念”的过程中，教师要循序渐进地引导学生，培养学生的抽象思维.同时合作交流符合《义务教育数学课程标准（2022年版）》的要求，是我国人才培养的需要.

2.4 鼓励知识整合，建立认知结构

在基于APOS理论的“实数”的教学中，鼓励学生对已学习过的数系进行分类与整合，有助于学生区分有理数与无理数的概念，理解实数概念的本质，培养分类思想，提高数学抽象能力，使数学概念系统化；同时，为高中数学继续扩充数系打下坚实的基础，也为高中数学中集合的学习做了铺垫.但是，分类思想的运用，要遵循数学概念分类的原则，避免分类重复或者遗漏的情况，从而体现数学的简洁之美、科学之美.

参考文献：

[1]曹一鸣.数学教学论[M].北京：高等教育出版社，2008.

[2]史宁中.学科核心素养的培养与教学——以数学学科核心素养的培养为例[J].中小学管理，2017（1）：35-37.

[3]史宁中.让学生爱上数学学习[J].中国基础教育，2023（8）：34-35.