基于生成对抗网络的离心泵时序数据异常检测*

李思汉,黄 倩,付 强*,张鑫宇,李云鹏

(1.江苏大学 流体机械工程技术研究中心,江苏 镇江 212001;2.中国核电工程有限公司,北京 100840; 3.核电泵及装置智能诊断运维联合实验室,江苏 镇江 212013)

0 引 言

随着人工智能的发展,机器学习进一步提升了旋转机械故障诊断的精度。机器学习五要素分别为:数据、模型、学习准则、优化算法和评价指标[1]。其中,数据是机器学习的基础,是进行模型训练和测试的要素。采用异常数据少和覆盖范围广的数据通常能够训练出良好的模型。

异常数据主要有两种:一种是由于设备故障或设备安装错误而产生的异常数据,另一种则是不符合正常数据分布的潜在相关性的数据[3]。

在采集离心泵运行数据时,难免会采集到上述两种情况的异常数据。因采集到的正常数据和异常数据是无标签数据,所以笔者选用更适用于无标签数据的无监督学习模型进行异常数据检测。

无监督学习模型的异常检测方法可分为以下4类:基于线性模型的方法、基于距离的方法、基于概率和密度估计的方法以及基于机器学习的方法。

许晓东等人[4]采用无监督学习K-Means聚类方法,对网络流量异常进行了检测,解决了异常数据检测中准确率低和误报警率高的问题;但k值的大小对K-Means聚类方法的影响较大,且对数据量较大的数据集处理能力较差。王晨曦等人[5]提出了一种基于阈值的聚类方法;但旋转机械数据呈多变性和突变性,故阈值的聚类方法不适用于进行离心泵的异常数据检测。

刘峰麟等人[6]采用了基于密度估计的空间聚类算法(density-based spatial clustering of applications with noise,DBSCAN),该算法可以根据数据特点来确定聚类半径和k值,解决了数据的异常检测问题和阈值选择问题;但密度估计的方法并不能用于处理数据量较大的时序数据。唐立等人[7]基于无人机产生的异常轨迹数据,提出了改进孤立森林的无监督学习算法,该算法可标明无人机异常数据类型和异常节点;但孤立森林算法随着数据量的增加,分割次数也随之增多,导致孤立森林的参数难以调整和固定[8]。

KO J U等人[9]对某火力发电厂的异常数据进行了研究,发现自编码器(AE)可以有效地对多维数据进行异常检测;但自编码器的重构能力较差。AN J等人[10]在自编码器的基础上,提出了变分自编码器(variational auto-encoders,VAE);但当变分自编码器处理未训练过的数据类型时,其检测能力较差。

生成对抗网络作为目前深度学习领域的新兴模型,受到了广泛的关注。它在生成图像和图像分类方面的成功应用,已经证明了该模型的杰出性能。此外,最近的研究发现,生成对抗网络可以处理序列形式的数据,这表明了生成对抗网络对时序数据进行异常检测方面的潜力。

综上所述,笔者提出采用生成对抗网络对离心泵时序数据进行异常检测的方法(该方法可以优化生成对抗网络,解决梯度消失问题),随后搭建离心泵异常数据检测试验台,基于试验数据训练生成器和判别器,将重构损失和判别损失构建成检测阈值,完成对离心泵异常数据的检测。

1 异常检测模型

1.1 GAN模型

与变分自编码器、深度信念网络等算法不同,生成对抗网络采用了隐式密度模型。它充分利用了神经网络的拟合能力,估算了数据分布的隐式密度函数[11-12]。

生成对抗网络异常数据检测训练模型与检测模型总体流程图如图1所示。

在训练模型时,向GAN模型中的生成器输入高斯分布白噪声,生成器会根据输入的白噪声随机生成时序数据,生成器在判别器的监督下不断提高生成水平,使得判别器对生成器所产生的数据判别为“真”。同时,进行训练的方式是将正常数据输入判别器中,提高判别器的判别能力。

判别器与生成器交替迭代训练时,如果生成器生成数据的能力过强,则会倾向生成容易“欺骗”判别器的数据。因此,当生成器与判别器达到纳什平衡时即认为训练完成。

笔者根据训练完成时生成器产生的重构损失和判别器产生的判别损失来构建阈值,利用构建的阈值来检测数据是否异常。

如图1右半部分所示,笔者使用传感器和振动采集仪,采集的信号会上传至上机位;采集的数据输入至训练好的生成器和判别器中,进而计算得到重构损失和判别损失;结合重构损失和判别损失构建异常损失值,若异常损失值超过阈值,则该数据为异常数据。

1.2 基础网络LSTM

LSTM是由ft∈[0,1]D、it∈[0,1]D、ot∈[0,1]D这3个门控制数据传递信息的。其中“0”代表“门”为关闭状态,“1”代表“门”为全开状态。LSTM网络中的“门”为“软门”,其值可在0到1中调节。输入门(it)调节当前时刻记忆单元(Ct′)中的信息保存数量;遗忘门(ft)调节上一时刻内部状态(Ct-1)中的信息遗忘数量;输出门(ot)调节当前时刻内部状态(Ct)输出给外部状态(ht)的信息数量[13]。

LSTM 3个门的计算公式表示如下:

it=σ(Wixt+Uiht-1+bi)

(1)

ft=σ(Wfxt+Ufht-1+bf)

(2)

ot=σ(Woxt+Uoht-1+bo)

(3)

式中:σ(·)为Logistic函数;W,U为系数组成的矩阵;b为偏执向量;xt为当前时刻的输入状态;ht-1为上一时刻的外部状态[14-16]。

首先,LSTM会结合上个时刻外部状态(ht-1)和当前输入状态(xt)来计算3个门控;其次结合遗忘门(ft)和输入门(it)来调控记忆单元(Ct′);最后由输出门与内部状态来确定外部状态(ht)。

ht的计算公式表示如下:

ht=ot⊙tanh(Ct),

(4)

式中:⊙为向量元素乘。

1.3 基于GAN的异常检测

离心泵数据采集为八通道同步采集,数据采集频率范围为8 Hz～204 kHz。数据异常检测即检测每个通道的数据是否处于异常状态[17-18]。训练GAN模型时的训练数据皆为正常数据,训练模型的目的是将正常数据标记为0,异常数据标记为1。

模型训练时,生成器和判别器会被看成一个整体。同时,整个生成对抗网络的目标函数被视为大小博弈的过程。

博弈公式表示如下:

(5)

式中:Pr为真实数据分布;P(z)为低维空间数据分布;θ,φ为生成器与判别器的参数;D(x),G(z)为生成器和判别器的映射函数[19-21]。

1.4 梯度消失问题解决

当真实数据分布(Pr)与生成数据分布(Pθ)不相交时,生成对抗网络会出现梯度消失的问题[22]。笔者提出了使用Wasserstein距离方法来解决上述问题。

当真实数据分布和生成数据分布不相交或相交点较少时,Wasserstein距离方法可用于对Pr与Pθ之间的距离进行计算。Wasserstein距离方法计算公式表示如下:

W(pr,pθ)=infγ～∏(pr,pθ)E(x,y)～γ[‖x-y‖]

(6)

式中:∏(Pr,Pθ)为Pr和Pθ组合起来的联合分布的集合;[║x-y║]为Pr和Pθ间的距离;γ为联合分布;E(x,y)～γ[║x-y║]为Pr和Pθ间的距离在联合分布下的期望值。

由于Wasserstein距离公式中的Infγ～∏(Pr,Pθ)无法直接求出,因此根据Kantorovich-Rubinstein对偶定理,笔者将该模型中的真实数据和生成数据分布之间的1st-Wasserstein距离转为1-Lipschitz连续函数期望差值的上界,有效解决了Infγ～∏(Pr,Pθ)无法直接求出的问题。

为了进一步优化,笔者提出了评价网络(f(x;φ))。评价网络同时满足K-Lipschitz连续函数的特点,使上界的计算变得更简洁,其上界公式表示如下:

(7)

1.5 异常检测方式

生成对抗网络对时序数据进行异常检测时,笔者采用了双重判别的方法。时序数据分别输入训练好的生成器和判别器,判别器通过判别损失来判断数据是否异常,生成器通过重构损失来判断数据是否异常。

在对异常数据进行检测时,测试数据和生成器的输出样本之间会产生一定的残差,残差的大小被作为判断数据是否异常的依据。因受到两时序数列起点、终点以及连续性等条件的约束,所以笔者使用适应性较强的动态时间扭曲方法(dynamic time warping,TW)来计算两时序数列的最小距离。其距离公式表示如下:

(8)

式中:ωk为初始两数列的度量。

再结合判别器的判别损失,笔者将两个判别标准结合,得到了异常检测损失值(δ),计算公式表示如下:

δ=λδG+(1-λ)δD

(9)

式中:δG为生成器的重构损失;δD为判别损失;λ为参数。

2 异常数据检测试验

2.1 试验装置

此处所用异常数据检测试验数据集由江苏省某泵站数据集和江苏大学流体机械工程技术研究中心试验台数据集组成。

卧式离心泵异常数据检测试验台如图2所示。

采集仪器详细参数如表1所示。

图2 卧式离心泵异常数据检测试验台Fig.2 Experiment bench for abnormal data detection of horizontal centrifugalpump 1为15 kW的电机;2为扭矩仪,设备型号为JCIA;3为振动传感器;4为力传感器;5为试验水泵,水泵为卧式离心泵,额定流量为100 m3/h,额定扬程为32 m,额定效率77.9%,转速2 900 r/min;6为进出口压力变送器;7为故障诊断信号采集仪,八通道同步采集且最大采集率为204 kHz,采集范围为±10 V电压信号模拟量,其内置恒流适配器可直接采集振动信号;8为上位机。

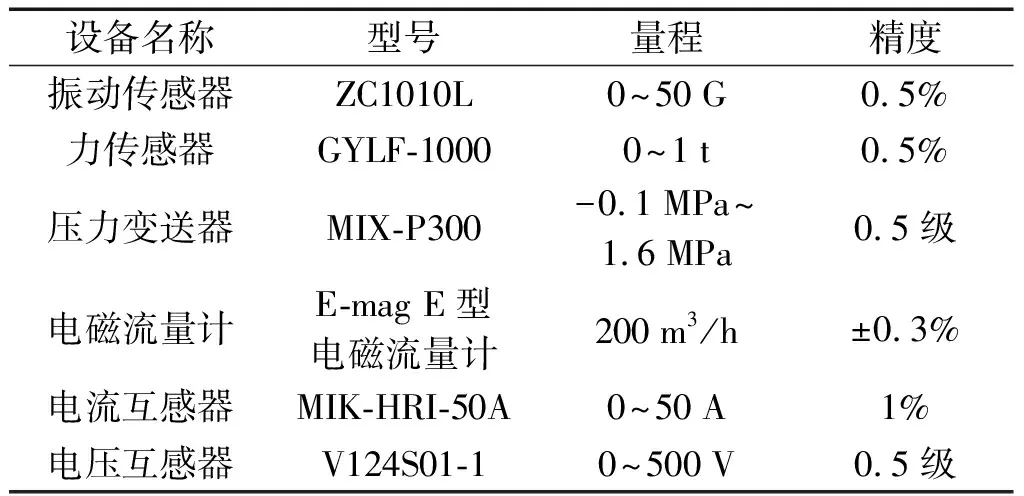
表1 采集设备参数表

计算机使用Windows 10 64位操作系统,LabVIEW的版本为2020版,Python版本为3.8。由LabVIEW采集和处理数据,并调用由Python编写的生成对抗网络代码来进行异常数据检测。

2.2 数据预处理

泵站共有4台立式离心泵,每2台水泵为一组,执行周轮换制。离心泵的参数为:扬程H=16 m,流量Q=2 700 m3/h,功率P=160 kW。此处以离心泵连续运行7天产生的数据作为泵站的数据集。

笔者提取泵站的正常数据的80%和试验台的正常数据的80%作为生成对抗网络模型的训练集。生成对抗网络模型的验证集包括泵站正常数据的20%、试验台正常数据的20%以及泵站和试验台数据中的异常数据。

笔者将采样频率设置为10 000 Hz,采样数设置为5 000。LabVIEW能够用于显示采集的数据并进行傅里叶变换。

数据异常原因及数据量如表2所示。

表2 数据异常原因及数据量

数据的时域对比图如图3所示。

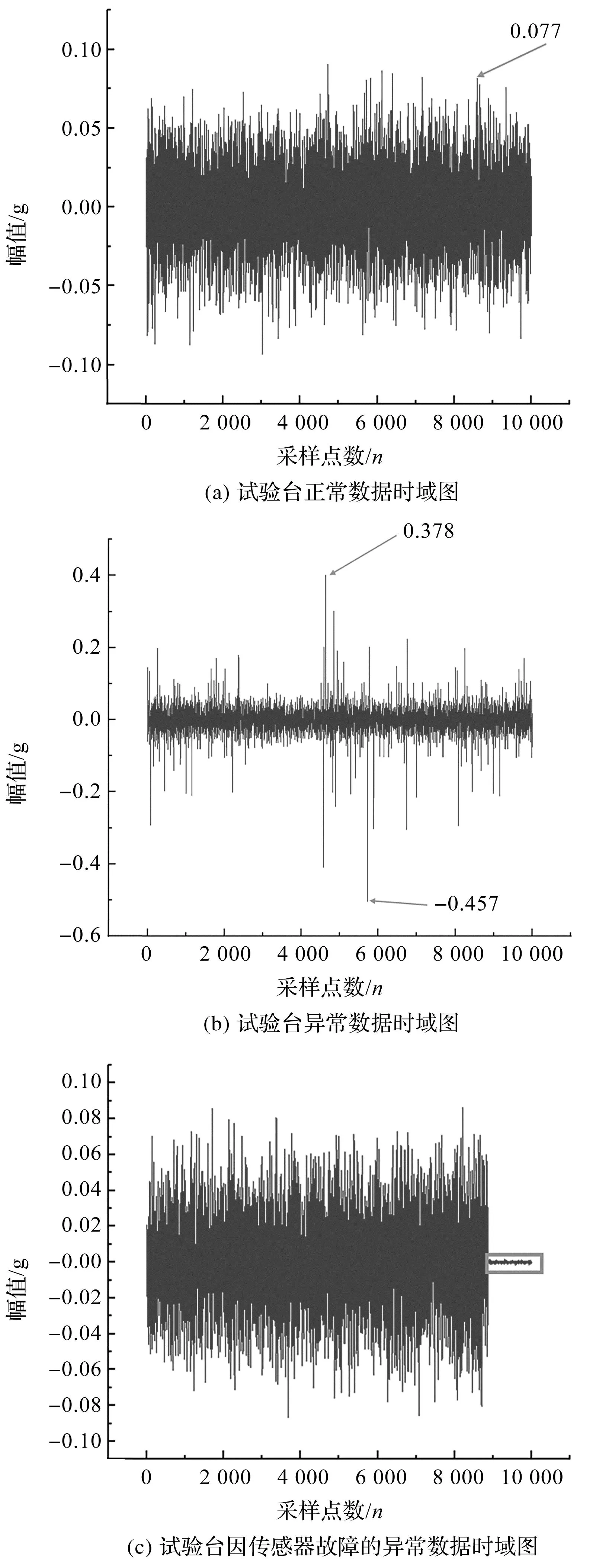
图3 数据时域对比图Fig.3 Time domain comparison of data

图3(c)中被圈出的数据是由于传感器故障而产生的数据,可见其幅值瞬间减小并持续到采样结束。采集后的数据在LabVIEW程序中同时进行时频域转换。

数据的频域对比图如图4所示。

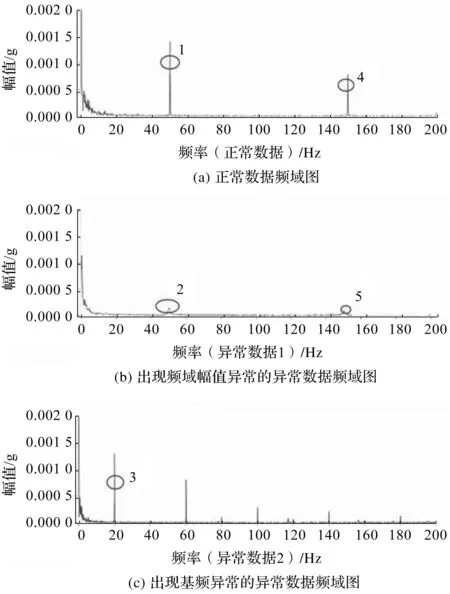
图4 数据频域对比图Fig.4 Comparison of data frequency domain

图4中的1和4区域分别为正常数据50 Hz和150 Hz中的频域幅值,特征较为明显。因试验数据100 Hz(二倍频)不够明显突出,所以不作为异常数据的判断依据。图4中的2和5区域为异常数据的频域幅值,其幅值远低于正常数据的幅值。图4中的3区域的基频在20 Hz,明显不同于正常数据的基频50 Hz。

2.3 评价指标

为验证生成对抗网络的异常数据检测能力,笔者将生成对抗网络与孤立森林、AE、K-Means算法和一类支持向量机(one-class support vector machine,OC-SVM)进行对比,并应用精确率(precision)、召回率(recall)和F1值来评估生成对抗网络的异常检测效果。评价指标公式表示如下:

(10)

(11)

(12)

式中:TP为实际数据正常,检测结果也为正常,即正样本被正确识别的数量;TN为实际数据异常,检测结果也为异常,即负样本被正确识别的数量;FP为实际数据异常,检测结果为正常,即误报的负样本数量;FN为实际数据正常,检测结果为异常,即漏报的正样本数量;Pre,Rec为精确率与召回率的缩写。

数据的优劣会影响旋转机械故障诊断模型的性能。如果正常数据被当成异常数据处理,数据将不够完整并丢失重要特征。因此召回率是评价异常数据检测模型性能的重要指标。

2.4 时序数据样本生成

在GAN模型训练过程中,生成器会根据采集到的数据生成逼真的数据样本。为了使生成器生成良好的数据,笔者在时域特征中选取1个特征,在频域特征中选取2个特征,观察训练过程中生成数据的特征分布,确定最佳训练轮次。

试验结果特征分布对比如图5所示。

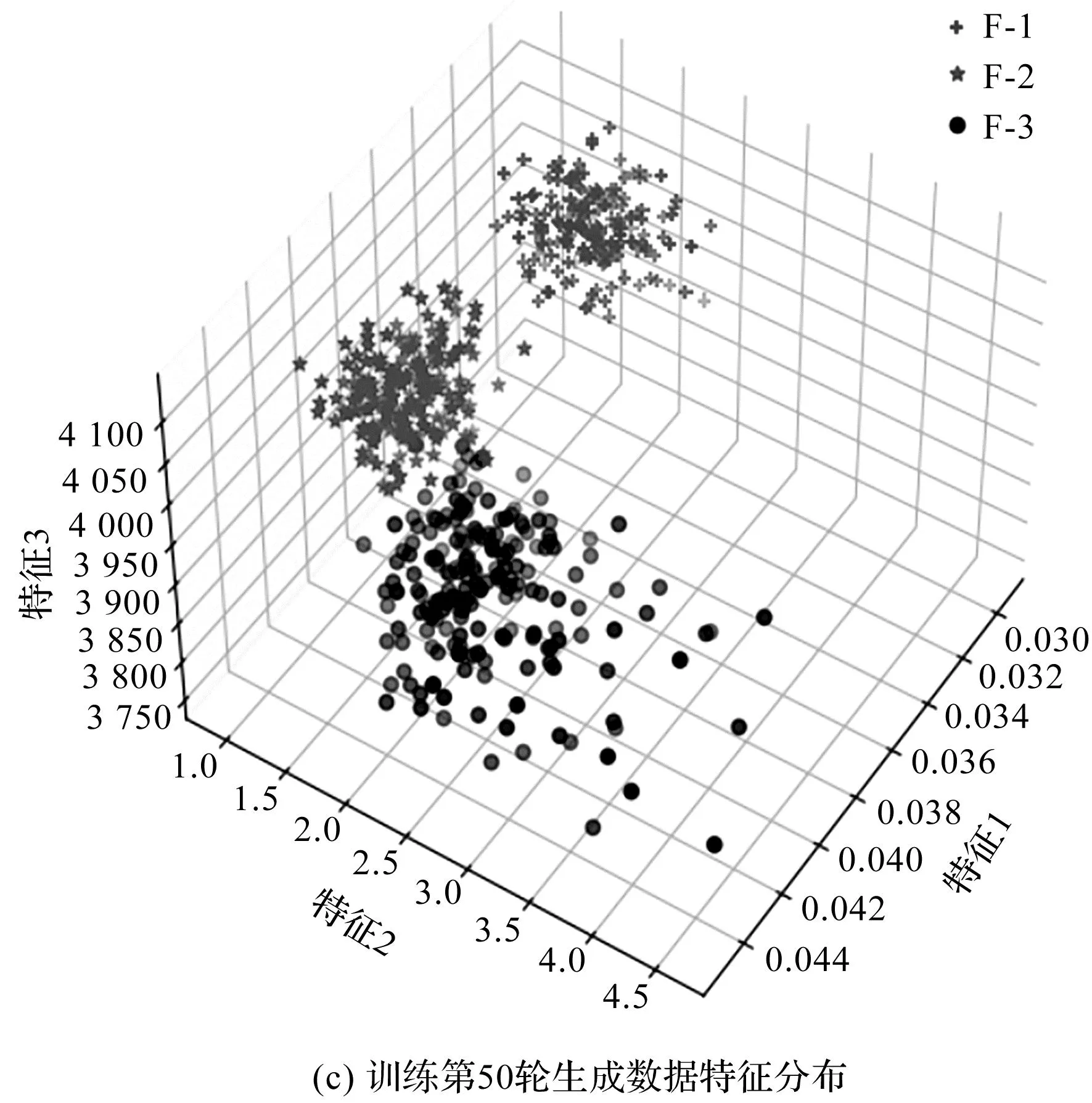
图5 试验结果特征分布对比图Fig.5 Comparison of experimental results feature distribution

由图5可知:通过多次试验对比发现,生成器训练50轮时可达到最优生成结果。

2.5 异常类型分类

在采集信号的过程中,传感器的稳定性十分重要。当传感器脱落或损坏时,传感器上传的数据将无法正确体现设备状态,并产生大量的异常数据。因此需要对发生该情形时所产生的异常数据进行报警。

笔者在试验中发现,当试验台发生传感器故障时,生成对抗网络平均重构损失值约为277。泵站发生传感器故障时,平均重构损失值约为271。为了防止出现传感器发生故障时,生成对抗网络未进行报警的情况,故笔者选用最低值271作为阈值。当重构损失超过阈值,以报警的方式提醒监测人员,设备可能出现故障。

3 结果分析

因泵站和试验台两组数据集略有差异,故笔者将两组数据集的结果取平均值并进行了分析。对于精确率这一指标,生成对抗网络约为89.5%,比AE平均值高2.5%,比孤立森林平均值高7.5%,高出K-Means平均值和OC-SVM平均值约20%;对于召回率这一指标,生成对抗网络为69.5%,比孤立森林平均值高9.5%,比K-Means平均值高18%,高出AE平均值和OC-SVM平均值约30%;对于F1值这一指标,生成对抗网络为78%,比孤立森林平均值高10%,比K-Means平均值高21%,同时也远高于AE和OC-SVM算法的平均值。

综合上述3个指标可以看出,生成对抗网络优于其他4种算法。尽管应用在试验台上比应用在泵站上的精确度略有下降,但从整体表现来看,生成对抗网络的精确率可达到90%左右,且召回率这一指标相比其他算法表现优异,表明生成对抗网络可以用于对离心泵的异常数据进行检测。

精确率对比结果如图6所示。

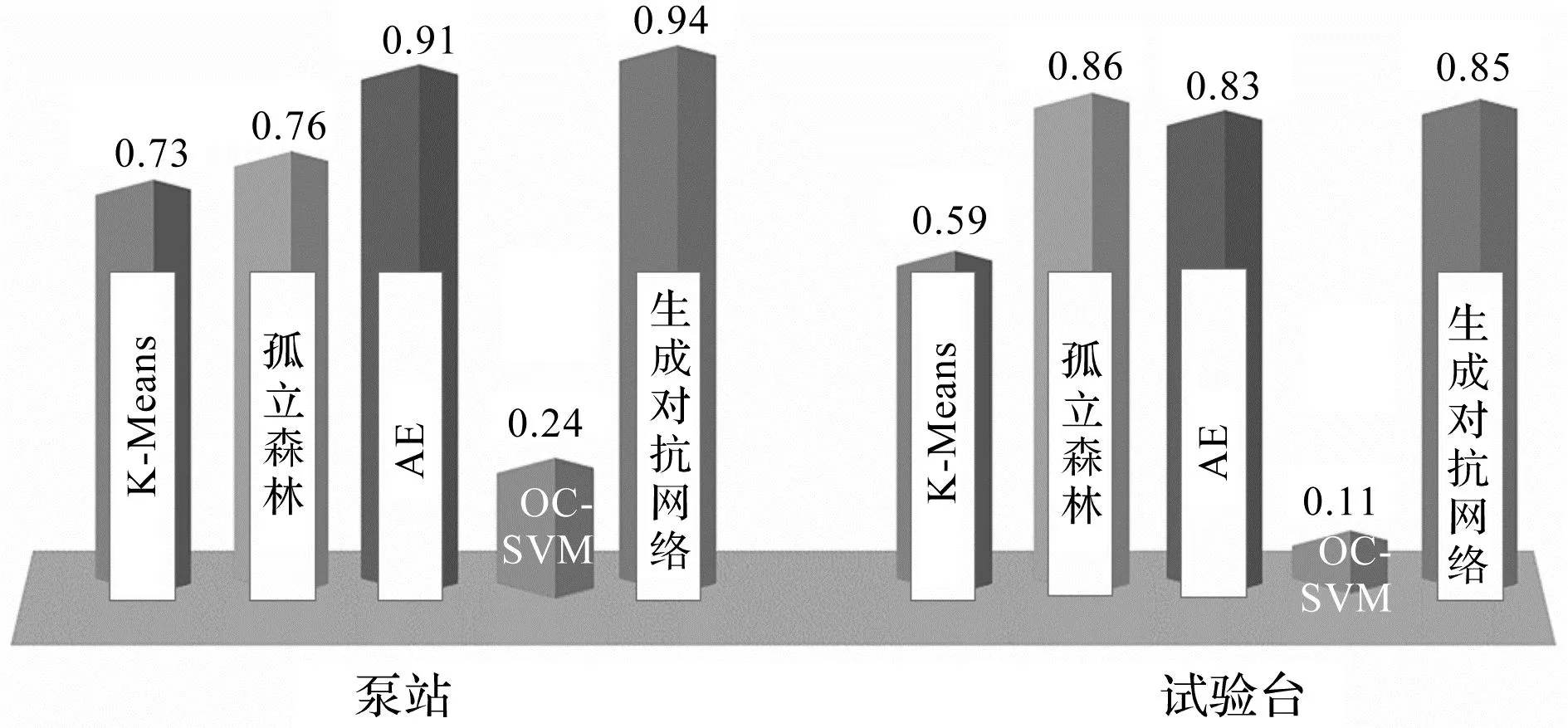
图6 精确率对比图Fig.6 Accuracy comparison chart

召回率对比结果如图7所示。

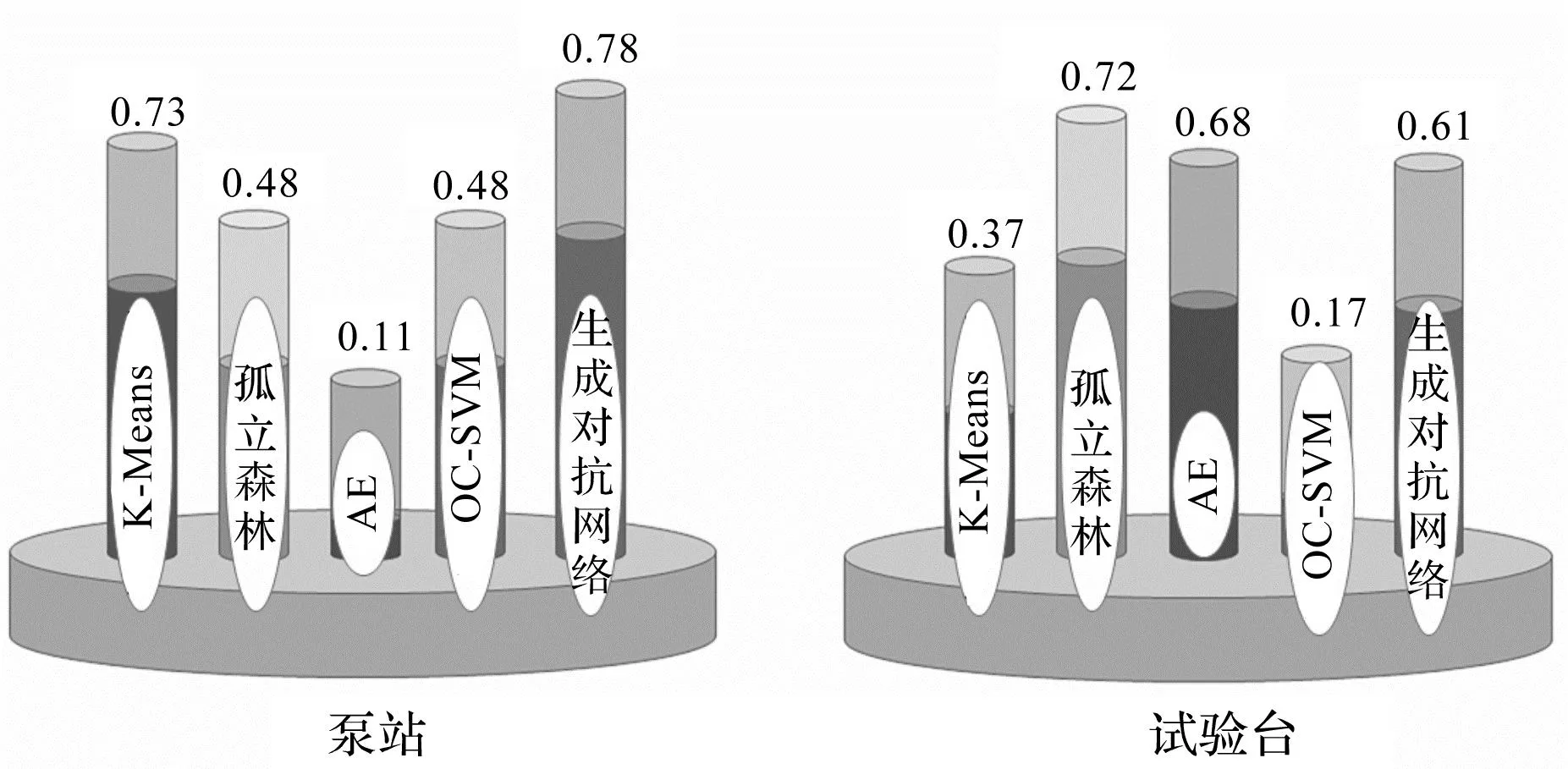
图7 召回率对比图Fig.7 Comparison of recall rates

F1值对比结果如图8所示。

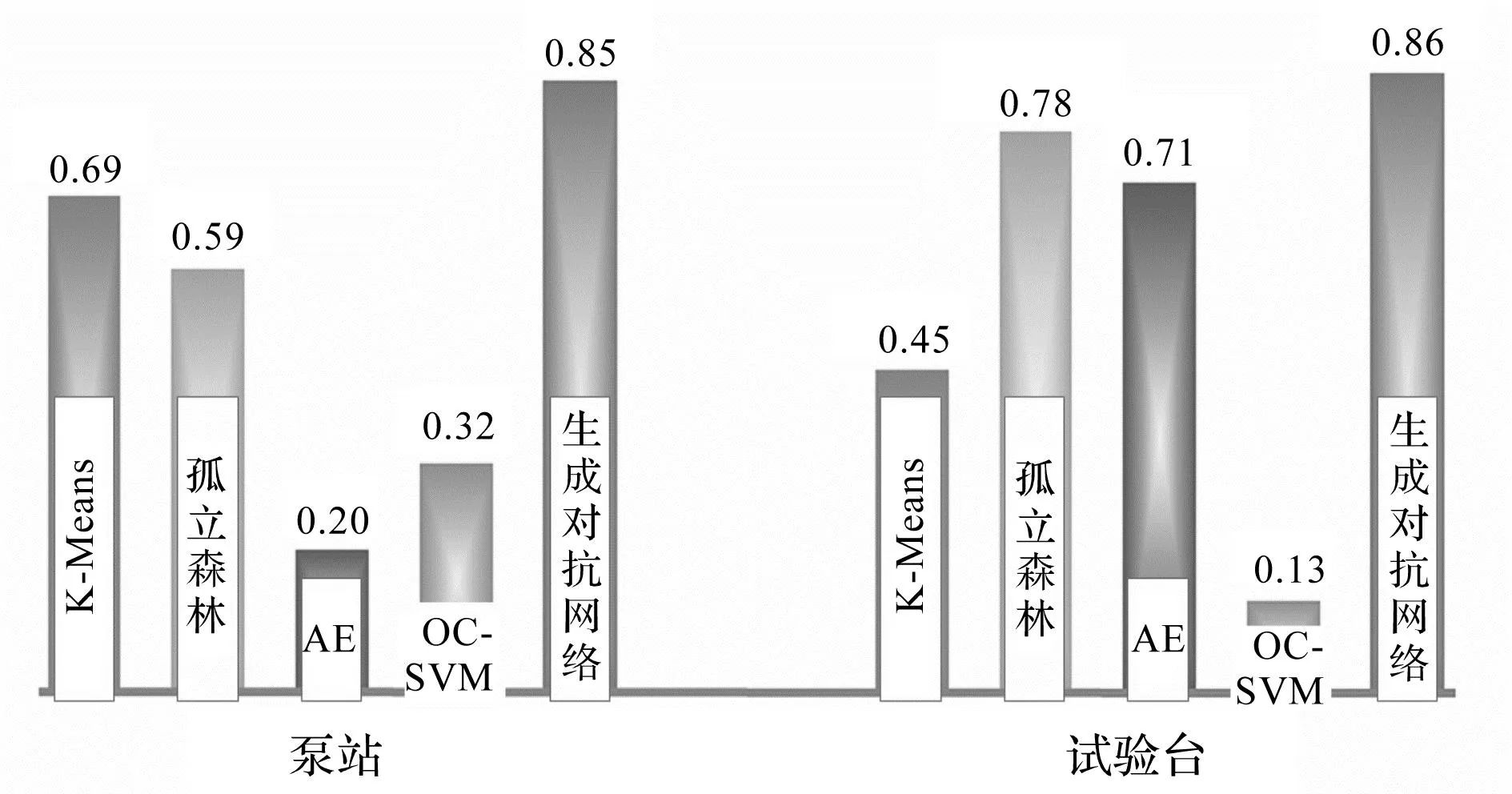
图8 F1值对比图Fig.8 Comparison of F1 scores

4 结束语

为了实现离心泵在线异常数据检测的目的,笔者提出了一种基于生成对抗网络的离心泵时序数据异常检测方法(该方法可以优化生成对抗网络,解决梯度消失问题)。

该方法通过在生成对抗网络中引入基础网络LSTM,以适应时序数据的特性,使用生成器和判别器对采集数据进行了双重检测,提高了异常数据检测的精度。

研究结论如下:

1)利用LabVIEW程序采集数据并进行了数据的预处理,利用频域中的倍频信息进行了初步的异常数据检测;

2)采用Wasserstein距离方法解决了生成对抗网络梯度消失的问题,增强了网络在现实中的可用性。生成对抗网络使用双重判别方法,增强了异常数据检测的能力;

3)试验结果表明,生成对抗网络在精确率、召回率和F1值3个评价指标中的表现良好,能够有效检测出异常数据。

在后续工作中,笔者将进一步优化算法,由单维数据异常检测提升为多维数据异常检测,以缩短异常数据检测的时间。