V形兜孔圆柱滚子轴承摩擦生热特性分析*
黄 杰,刘延斌*,李旭莹,桑得雨,宁 仲
(1.河南科技大学 机电工程学院,河南 洛阳 471003;2.中国铁建重工集团股份有限公司,湖南 长沙 410100; 3.洛阳轴承研究所有限公司,河南 洛阳 471039)
0 引 言
航空发动机主轴通常都采用圆柱滚子轴承作为承载和运动传递的关键零件,其性能直接影响整机的可靠性和使用寿命[1]。
在高速、轻载的工作条件下,圆柱滚子轴承常出现打滑现象,且相互接触的轴承各部件间由于碰撞摩擦剧烈会导致轴承摩擦生热严重,引起轴承温度升高,造成结构热变形而使轴承卡死。据统计,航空发动机主轴轴承25%的失效是由轴承部件间的摩擦生热引起的[2]。
在高速、轻载工作条件下,V形兜孔圆柱滚子轴承有较好的稳定性和防打滑性能[3],这对于提升主轴传动性能至关重要。因此,深入研究V形兜孔圆柱滚子轴承的摩擦生热特性,对提高其实际应用具有重要的现实意义。
王黎钦等人[4]建立了圆柱滚子轴承拟静力学模型,考虑了轴承内部各种接触力和摩擦力的相互作用,研究了转速、载荷等工况对轴承内外圈滚道、兜孔、套圈引导面等热源摩擦生热的影响规律;但其忽略了滚子自转引起的搅油摩擦生热。陈观慈等人[5]基于球轴承拟静力学和摩擦生热分析模型,分析了球自旋生热、球与内外滚道滑动摩擦生热和保持架与套圈引导面摩擦生热,研究了不同工况对轴承局部摩擦生热和总摩擦生热的影响规律;但其忽略了球与保持架兜孔的滑动摩擦生热。MA Fang-bo等人[6]建立了球面滚子轴承摩擦生热模型,分析了滚子与滚道、滚子与兜孔、保持架与内圈引导面和滚子搅拌力产生的摩擦功耗,研究了速度、载荷、径向游隙等对轴承摩擦生热的影响;但其未考虑滚子与兜孔运行过程中接触状态的变化。王燕霜等人[7]利用拟静力学法分析了不同转速、载荷下,轴承保持架与引导面、球与滚道、兜孔等摩擦功耗损失,得到了结论,即转速和轴向载荷的改变对轴承各部件摩擦功耗影响较大,而径向载荷的改变对摩擦功耗的影响较小;但该研究中的滚子与滚道的接触模型忽略了油膜厚度的影响。LI Jun-ning等人[8]建立了考虑打滑的高速轻载滚动轴承摩擦功耗损失模型,模型计算结果表明,随着打滑率的增加,轴承内外套圈的摩擦功耗也随之增加,而保持架引导面和滚子搅油的摩擦功耗则呈相反趋势;但其在功耗模型中对滚子与兜孔的摩擦生热考虑欠缺。TAKABI J等人[9]基于Palmgren经验公式,建立了球轴承摩擦生热分析模型,研究了球与内滚道、保持架与引导面以及润滑油黏性阻力造成的摩擦功耗损失;但该模型多适用于中低转速轴承,因此具有一定的局限性。
综上所述,国内外对滚子轴承摩擦生热的研究多集中于滚子与滚道、保持架与套圈引导面,而对滚子轴承兜孔摩擦生热的研究较少,对具有特殊兜孔结构的轴承生热特性研究更为鲜见。V形兜孔圆柱滚子轴承虽具有良好的稳定性和防打滑性能,但V形兜孔几何参数对兜孔摩擦生热的影响尚不明确。
因此,为给V形兜孔圆柱滚子轴承摩擦生热特性研究提供理论依据,在多体动力学理论和摩擦学原理的基础上,笔者利用保持架V形兜孔结构建立轴承热分析模型,探讨高速、轻载工况下不同兜孔几何参数对兜孔摩擦生热的影响,研究兜孔几何参数优化后的轴承摩擦生热特性。
1 V形兜孔轴承热分析模型
1.1 轴承V形兜孔结构
圆柱滚子轴承V形兜孔结构如图1所示。
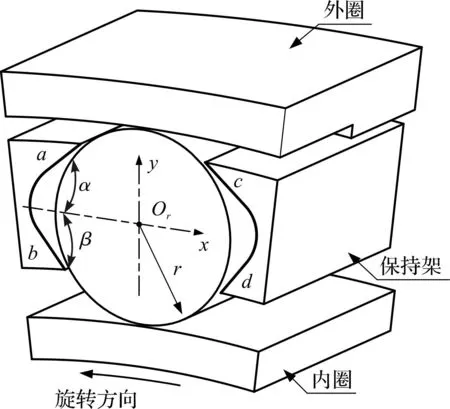
图1 V形兜孔结构示意图Fig.1 V-shaped pocket structure diagramOr为滚子质心;α为兜孔a、c为壁面的倾斜角度;β为兜孔b、d壁面的倾斜角度;r为滚子半径。
图1中,V形兜孔结构在径向平面内对滚子有较好的定位和引导精度,可降低滚子运动过程中与兜孔的碰撞频率。
1.2 轴承动力学模型
1.2.1 滚子与兜孔接触模型
V形兜孔圆柱滚子轴承滚子与兜孔的接触模型如图2所示。
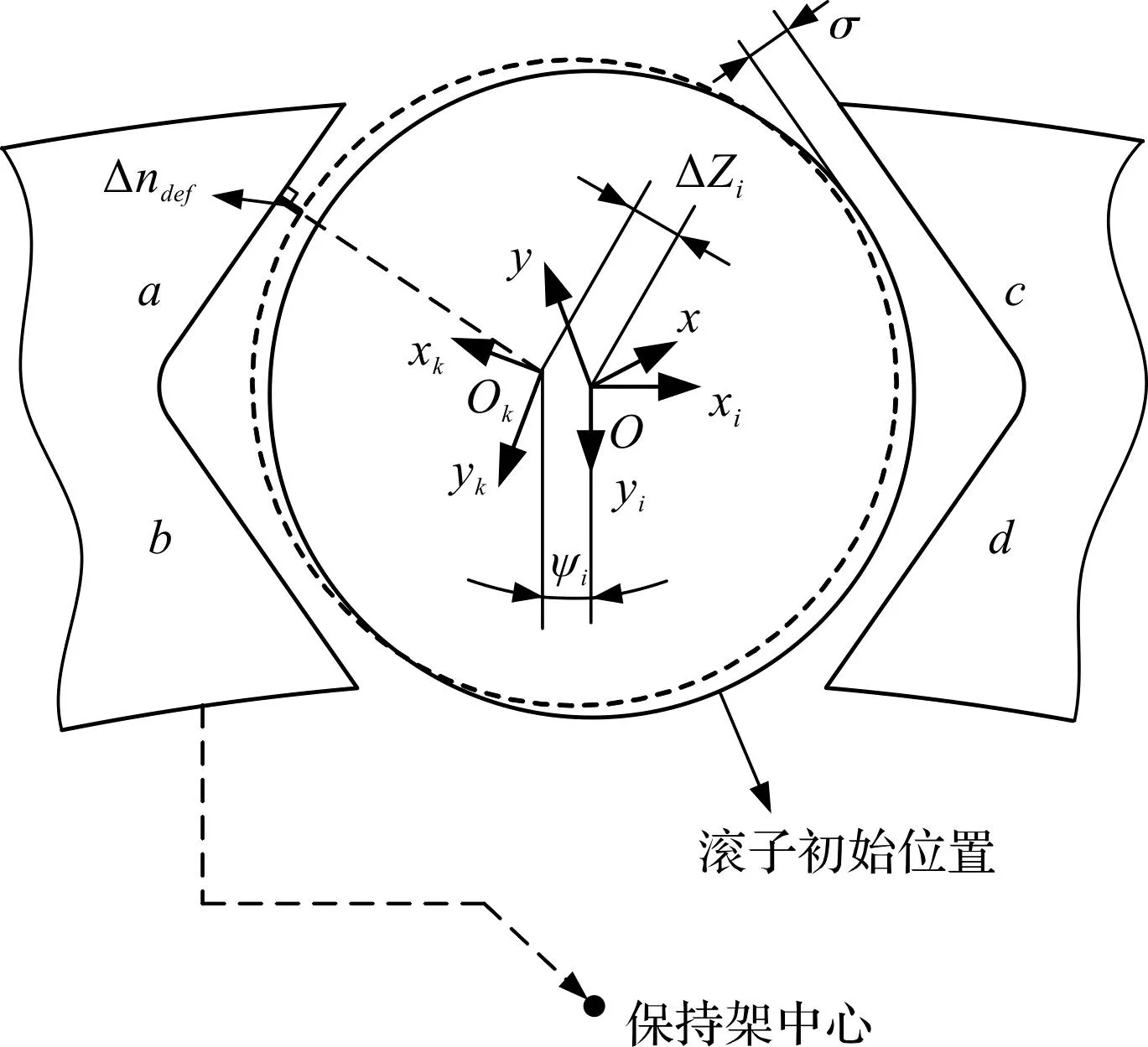
图2 滚子与兜孔接触模型Fig.2 Roller and pocket contact model {O,x,y}为兜孔几何中心坐标系;{O,xi,yi}为滚子理想中心坐标系,由运动过程中滚子的位置确定;{Ok,xk,yk}为滚子质心坐标系。
图2中,因滚子与兜孔壁接触时产生的法向接触力和切向摩擦力的相互作用,导致滚子与兜孔壁的接触变形;滚子与兜孔壁未接触时,二者之间仅存在流体动压作用[10]。
由于轴承主要承受径向载荷,为减少工作量,笔者假定轴承外圈固定,内圈旋转,对滚子和保持架施加平面约束,使轴承整体在径向平面内运动。
滚子与兜孔壁间的最小间隙为:
Δndef=ΔZi-σ
(1)
式中:n为兜孔壁面(n=a,b,c,d);σ为兜孔间隙;ΔZi为滚子质心在理想坐标系中圆周分量的绝对值。
ΔZi可表示为:
ΔZa=ΔZc=xri·cosψi·sinα
(2)
ΔZb=ΔZd=xri·cosψi·sinβ
(3)
式中:xri为滚子质心在理想坐标系中xi方向上的移动分量;ψi为滚子质心的角位移。
当滚子与兜孔间最小油膜厚度Δcl≥Δndef≥0时,滚子与兜孔壁之间受到Hertz线接触和流体动压的共同作用,其法向接触力为:
(4)
式中:δnri为渗透量,δnri=Δcl-Δndef;η为润滑油黏度;vi,vpi为滚子和兜孔的切向速度;Kcl为滚子与兜孔间的线接触刚度系数[11];Ccl为滚子与兜孔间的Lee-wang阻尼系数[12];l为滚子长度。
滚子与兜孔壁面的摩擦力为:
Tnri=μFnri
(5)
式中:μ为摩擦系数,根据滚子与兜孔间的滑动摩擦关系,μ取0.16。
当Δndef>Δcl时,滚子与兜孔壁面在流体动压作用下,其法向接触力为:
(6)
滚子与兜孔壁面的摩擦力为:
(7)
为节省篇幅,关于滚子与套圈滚道、保持架与套圈引导面的接触模型可参见文献[3]580-582。此处不再详述。
1.2.2 滚子的动力学方程
第i个滚子的牛顿方程为:
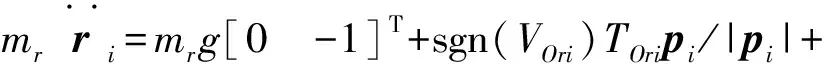
γa=[-cos(κc+τi-α) -sin(κc+τi-α)]T,
γb=[cos(κc+τi+β) -sin(κc+τi+β)]T,
医院供应室具有科室的特殊性,主要负责医院各个科室的医疗物品,如:无菌器械、敷料和一次性无菌物品的清洗和消毒,同时也承担着医疗器械的回收工作。通常情况下,供应室工作质量的好坏与医疗质量和护理质量有着直接关系,其不仅会对院内感染的质量控制造成直接影响,同时会对患者的生命安全构成危及[1]。为此,本院对持续性质量改进在医院供应室管理工作中的效果进行分析,并总结分析结果,现报告如下。
γc=[-cos(κc+τi+α) sin(κc+τi+α)]T,
γd=[cos(κc+τi-β) sin(κc+τi-β]T,
ξa=[sin(κc+τi-α) -cos(κc+τi-α)]T,
ξb=[sin(κc+τi+β) cos(κc+τi+β)]T,
ξc=[sin(κc+τi+α) cos(κc+τi+α)]T,
ξd=[sin(κc+τi-β) -cos(κc+τi-β)]T,
ri=[xiyi]T,rir=[xiryir]T,
pi=[-ykxk]T,pir=[ei0]T
(8)
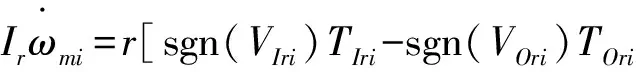
(9)
式中:mr为滚子的质量;Ir为滚子的转动惯量;xi,yi为第i个滚子在理想坐标系中X、Y坐标;xir,yir为内圈在惯性坐标系中X、Y坐标;xk,yk为第i个滚子在质心坐标系中X、Y坐标;FIri为第i个滚子与内滚道的法向接触力;FOri为第i个滚子与外滚道的法向接触力;TIri为第i个滚子与内滚道的切向摩擦力;TOri为第i个滚子与外滚道的切向摩擦力;Fari,Fbri,Fcri,Fdri和Tari,Tbri,Tcri,Tdri分别为第i个滚子与a、b、c、d4个兜孔壁面的法向接触力和切向摩擦力;κc为保持架角位移;τi为滚子初始转角。
1.2.3 保持架动力学方程
保持架的牛顿方程为:
(10)
保持架的欧拉方程为:
Fcri(ri-rb)Tξc-Fdri(ri-rb)Tξd}-mbg-
(11)
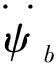
1.3 轴承摩擦功耗模型
V形兜孔圆柱滚子轴承摩擦功耗模型如图3所示。
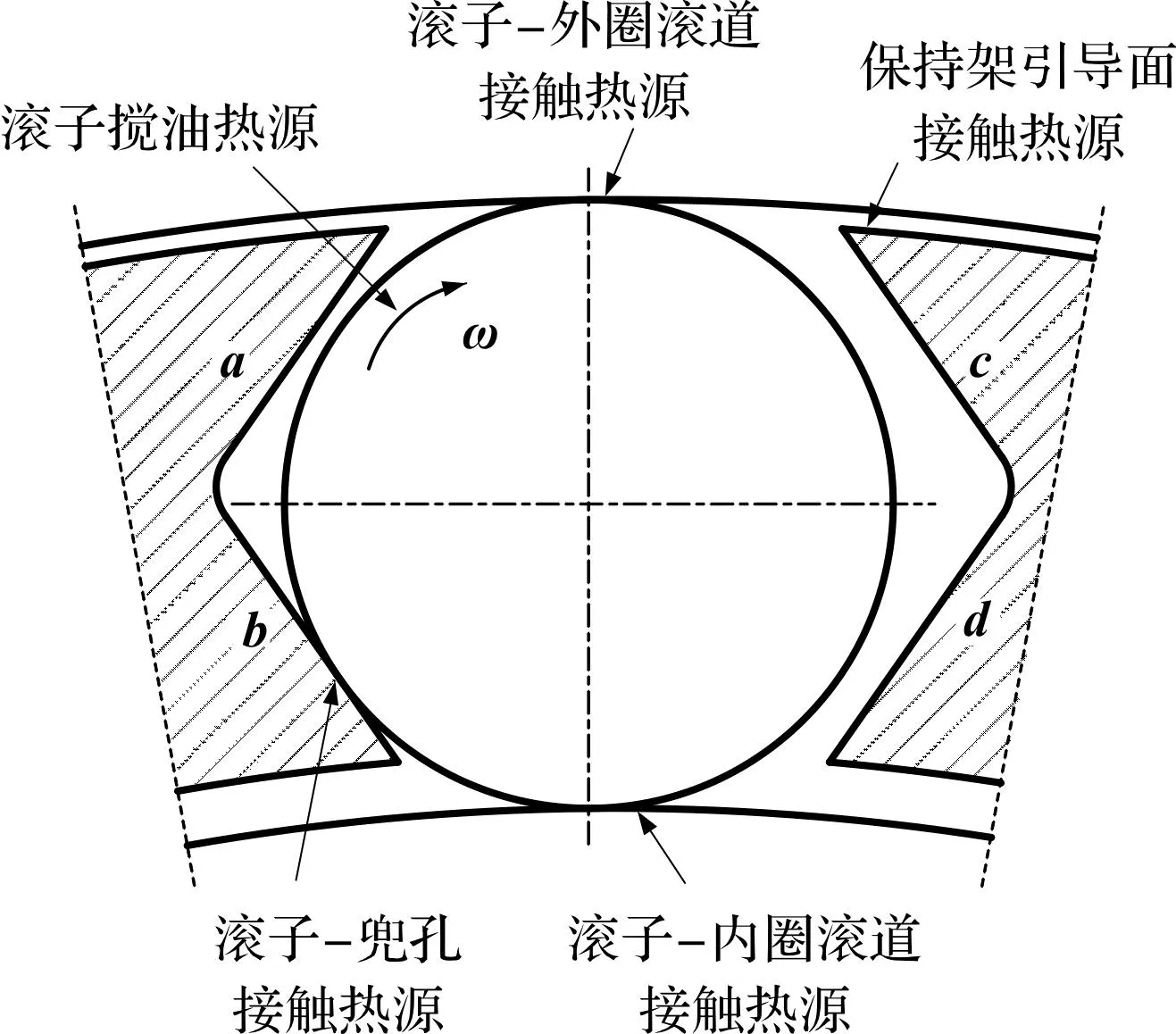
图3 轴承摩擦功耗模型Fig.3 Analysis model of bearing frictional power consumption
各热源因摩擦生热产生的摩擦功耗包括[13]:滚子与滚道、滚子与兜孔、保持架与套圈引导面间的滑动摩擦功耗和滚子搅油摩擦功耗。
因航空发动机主轴用圆柱滚子轴承在工作时主要承受径向载荷,滚子端面与套圈挡边轴向接触负荷较小,故忽略滚子端面与套圈挡边间的滑动摩擦功耗。
各热源产生的摩擦功耗计算方法为:
1)滚子与兜孔的滑动摩擦功耗
V形兜孔因其结构特殊,相较于普通兜孔具有多个兜孔壁面,使得滚子与兜孔的接触关系较为复杂。并且运转过程中滚子与兜孔的接触位置不断变化,导致滚子与兜孔各壁面间的接触力和摩擦力的不同。因此,滚子与兜孔间的摩擦功耗可由滚子与各个兜孔壁面间摩擦功耗的总和来表征,即:
(12)
式中:Dr为滚子直径;ωmi为滚子自转角速度;n为滚子个数;
2)滚子与滚道的滑动摩擦功耗
其公式如下:
(13)
式中:VNri为滚子与内、外滚道因转速差而产生的相对滑动速度,N=I,O。
根据各部件间的动态关系,滚子与内、外滚道的相对滑动速度可表示为:
(14)
(15)
式中:ri为轴承内滚道半径;ro为轴承外滚道半径;r为滚子半径;ni为轴承内圈转速;nmi为滚子自转速度;nri为滚子公转速度;
3)滚子的搅油摩擦功耗
其公式如下:
(16)
式中:Dm为节圆直径;υ为润滑油油气混合密度;Cv为润滑油黏着拖动系数;ωri为滚子公转角速度;
4)保持架与套圈引导面的滑动摩擦功耗
其公式如下:
(17)
式中:Db为保持架引导面直径;ωc为保持架角速度;ωi为内圈角速度;
5)轴承总摩擦功耗
其公式如下:
Htotal=Hxi+HNi+Hfi+Hg
(18)
1.4 轴承模型求解及流程图
轴承动力学模型和摩擦功耗模型求解流程图如图4所示。
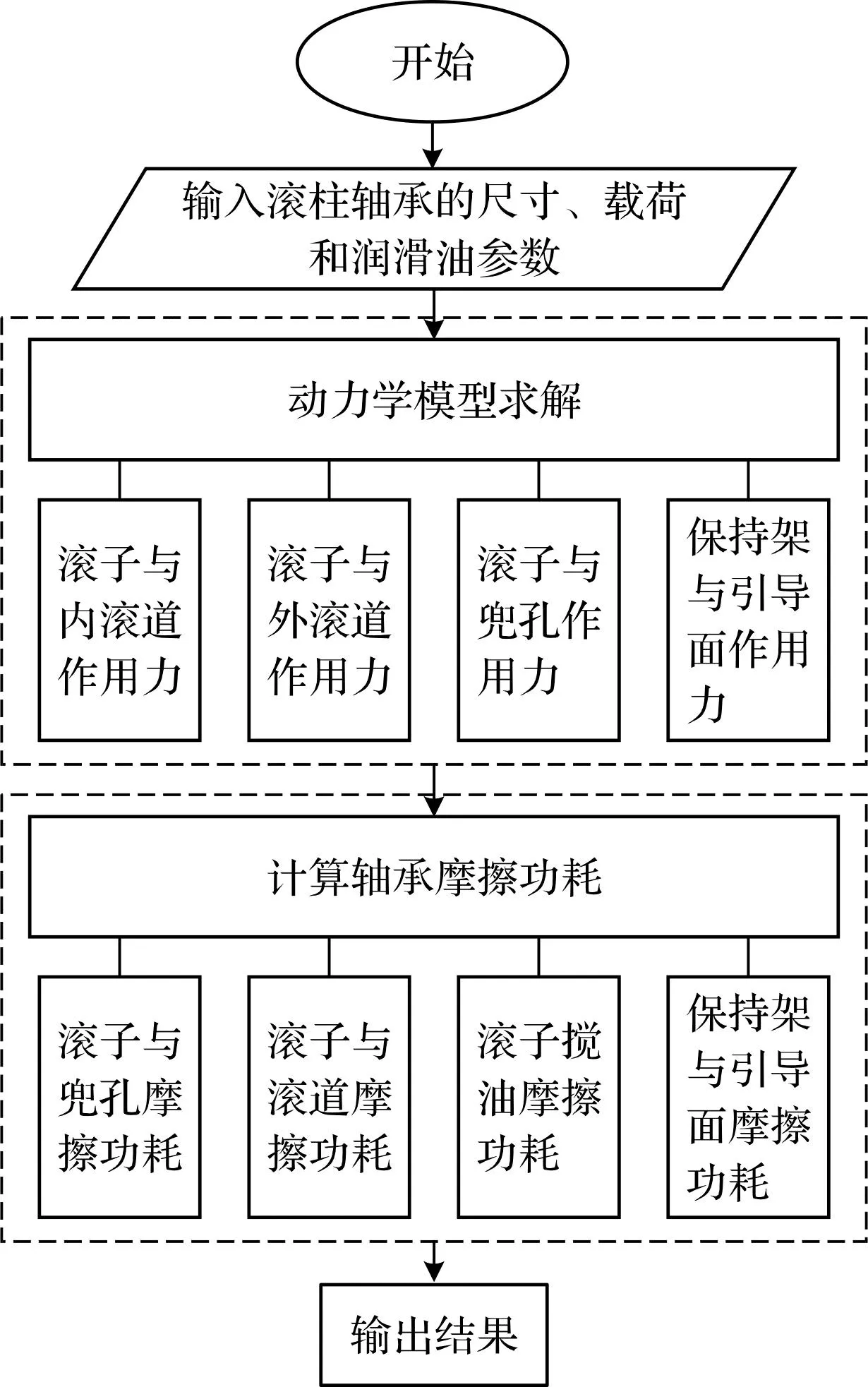
图4 轴承模型求解流程图Fig.4 Bearing model solution flow chart
在轴承动力学和摩擦功耗模型的基础上,V形兜孔壁倾角α=40°,β=40°时,在内圈转速24 000 r/min,径向载荷分别为100 N、900 N的工况下,笔者对滚子与兜孔间瞬态摩擦生热进行仿真计算。
滚子与兜孔间的摩擦生热时间变化曲线如图5所示。
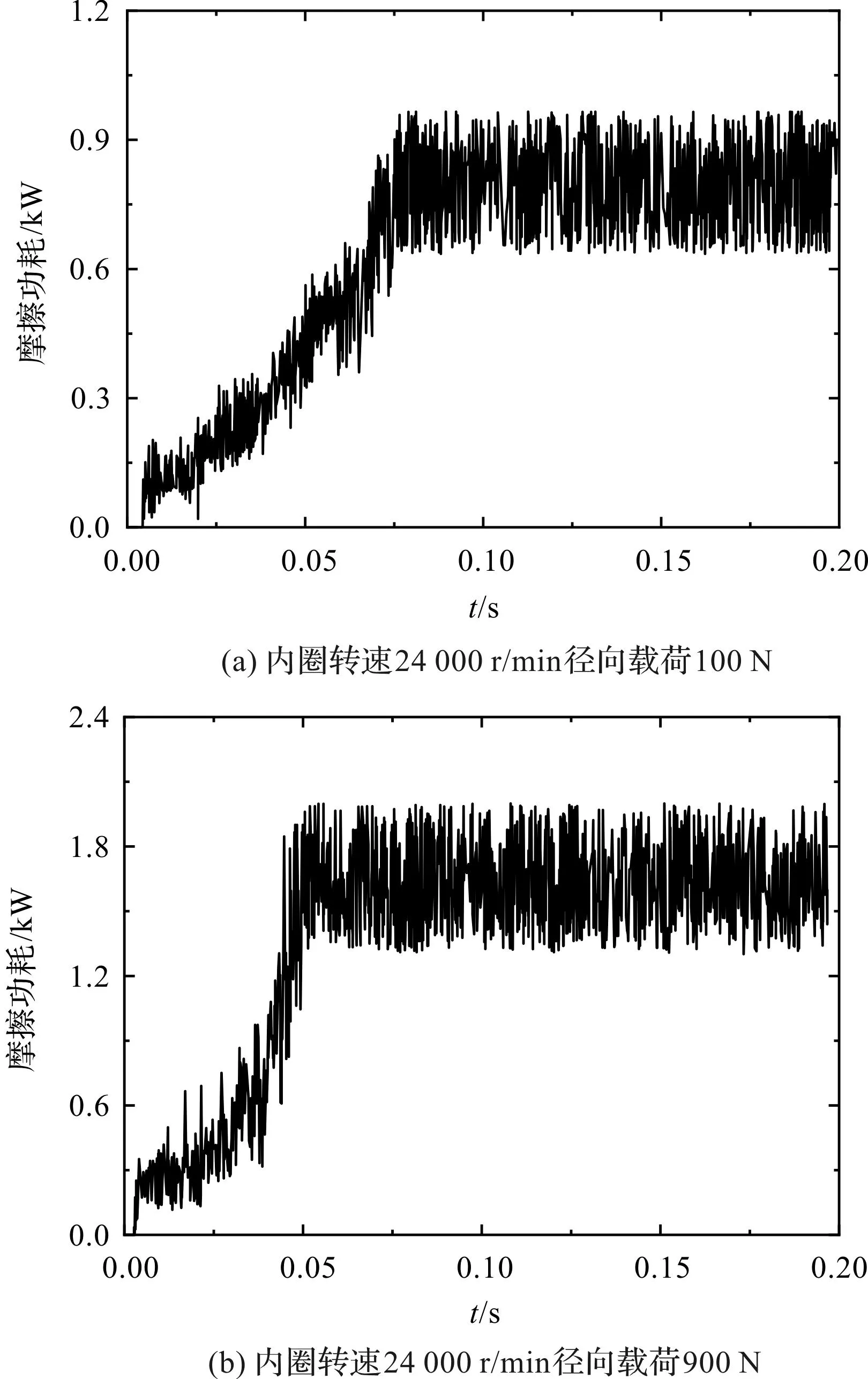
图5 兜孔摩擦生热时变曲线Fig.5 Time variation curve of cage pocket frictional heat generation
由图5兜孔摩擦生热的变化趋势可知:时间的变化使得摩擦生热曲线持续波动,不利于在给定工况下确定兜孔的摩擦功耗;但随时间的增加,轴承各部件间的运动关系逐渐趋于稳定状态,兜孔摩擦生热的波动幅值也逐渐趋于稳定。
因此,为了凸显不同转速和载荷下兜孔壁倾斜角度对兜孔摩擦生热以及对轴承各部件摩擦生热的影响,同时为了突出重点、节省篇幅,笔者取轴承瞬态摩擦生热稳定阶段的均值进行结果分析。
2 V形兜孔摩擦生热特性及参数优化
2.1 理论分析模型可靠性验证
针对该轴承,笔者采用文献[14]中圆柱滚子轴承的主要几何参数,并运用上述建模方法,建立其动力学和摩擦功耗模型,求解得出不同工况下该轴承的摩擦功耗,并对比分析仿真结果和文献中的试验结果,以验证笔者所提出的轴承动力学模型和摩擦功耗模型的可靠性。
轴承仿真结果与试验结果对比如图6所示。
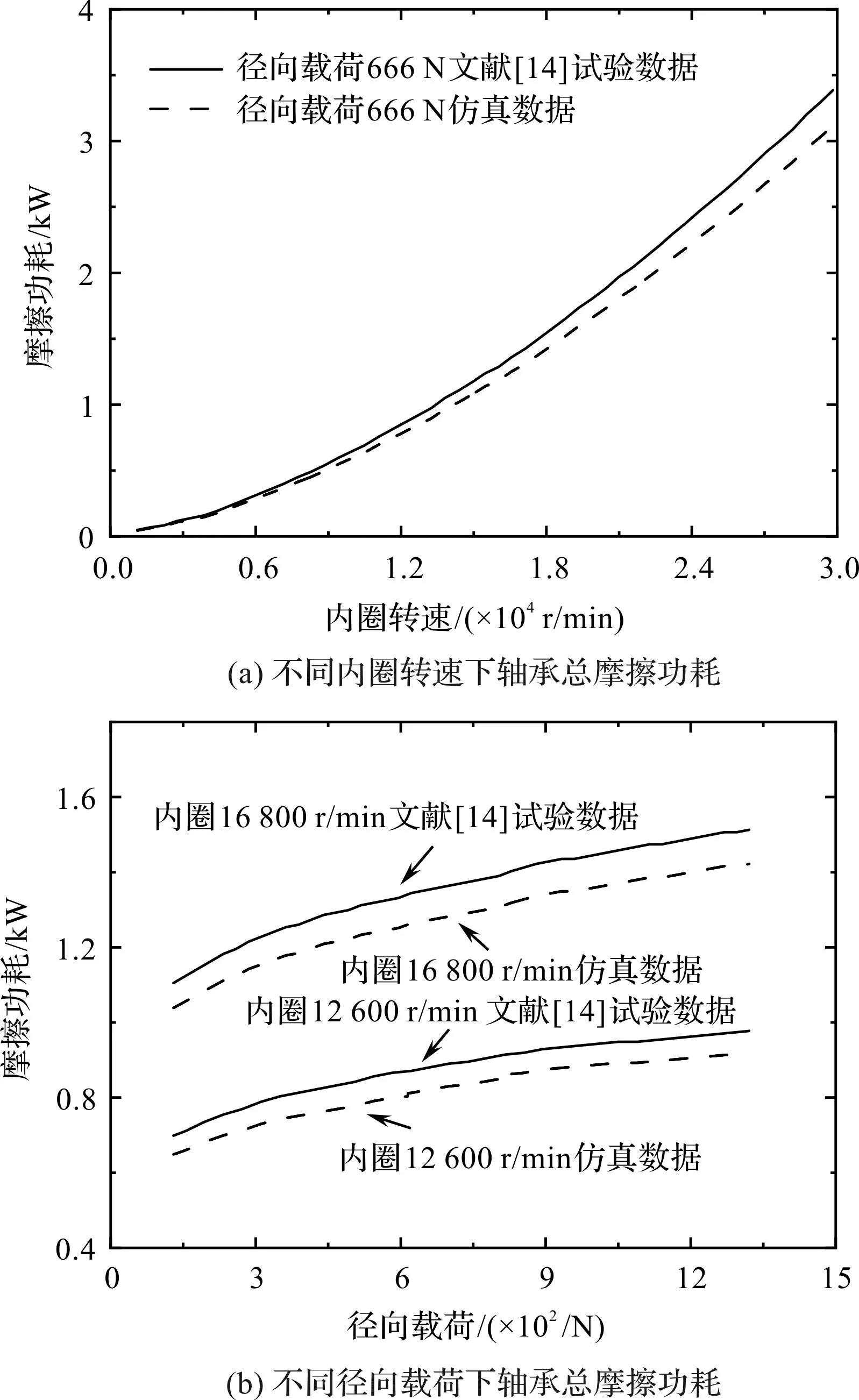
图6 不同内圈转速下轴承总摩擦功耗Fig.6 Comparison between simulation results and experimental results
图6(a)为径向载荷666 N时,不同内圈转速下轴承摩擦功耗的对比曲线;图6(b)为内圈转速12 600 r/min和16 800 r/min时,不同径向载荷下轴承摩擦功耗的对比曲线。
由图6可知:利用笔者建立的理论分析模型所获得的轴承摩擦功耗仿真结果与文献[14]试验结果吻合较好,呈现出相同的变化规律,表明笔者提出的理论分析模型具有较高的可靠性。
2.2 兜孔参数对兜孔摩擦生热的影响
2.2.1 轴承主要参数
V形兜孔圆柱滚子轴承的主要几何参数如表1所示。
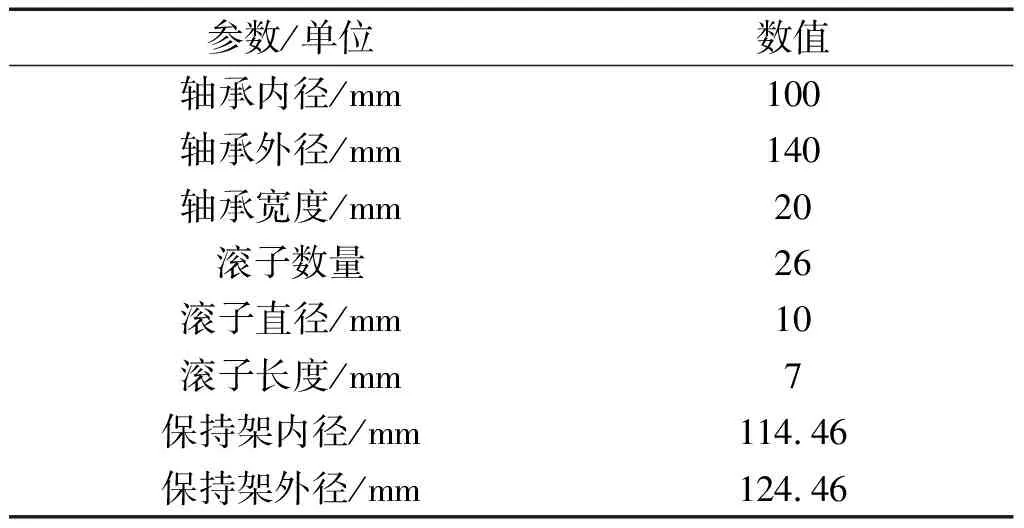
表1 轴承主要几何参数
材料特性参数如表2所示。

表2 轴承材料特性参数
笔者选用4109航空润滑油[15]为轴承润滑,其参数如表3所示。

表3 4109航空润滑油主要参数
2.2.2 不同转速下的影响
当径向载荷为100 N,内圈转速范围为12 000 r/min~24 000 r/min,V形兜孔壁倾角α、β分别取不同值时,在考虑实际生产中轴承可制造性的前提下,笔者对滚子与兜孔间的摩擦生热进行仿真计算。
滚子与兜孔摩擦生热结果如图7所示。
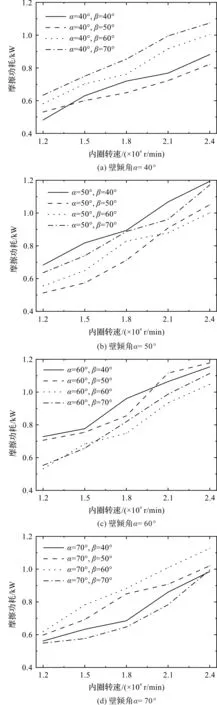
图7 不同转速下兜孔几何参数对兜孔摩擦生热的影响Fig.7 Effect of pocket geometry parameters on frictional heat generation of pocket under different speeds
由图7可知:不同V形兜孔几何参数下,兜孔摩擦功耗都随着转速的增加呈非线性增大趋势。这是因为随着内圈转速的升高,保持架稳定性降低,滚子与兜孔的滑动速度增加,滚子与兜孔壁间的作用力变大,导致兜孔摩擦生热持续升高[16]。
图7(a)~图7(d)分别为在壁倾角α倾斜角度给定的情况下,在同一径向载荷、不同内圈转速的工作条件下,壁倾角β取不同值时兜孔的摩擦功耗。当α倾角一定时,β倾角的改变对兜孔摩擦生热的影响较大。这是因为随着内圈转速的升高,β角越大,兜孔的定位精度降低,滚子与兜孔的碰撞频率加快,位置关系不断变化,使得滚子与兜孔的滑动摩擦剧烈,造成兜孔摩擦生热显著上升。
但不同壁倾角组合导致兜孔摩擦生热、升高趋势不同,转速相同且径向载荷为100 N时,不同壁倾角组合下兜孔摩擦功耗最大差值为393.7 W。
2.2.3 不同载荷下的影响
当内圈转速为24 000 r/min,径向载荷范围为100 N~900 N,V形兜孔壁倾角α、β分别取不同值时,笔者对滚子与兜孔间的摩擦生热进行仿真计算。
滚子与兜孔摩擦生热结果如图8所示。

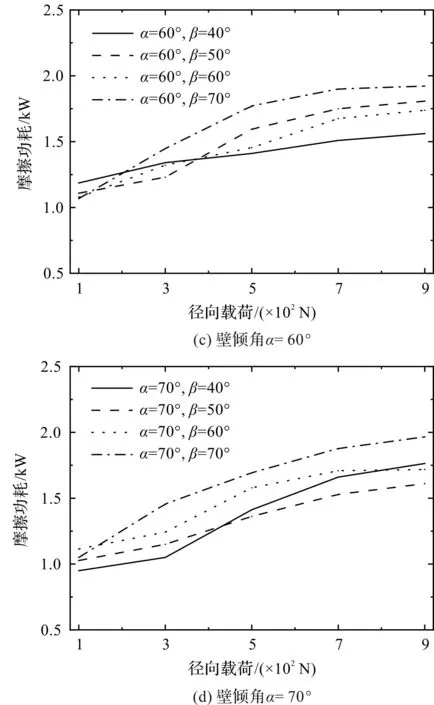
图8 不同载荷下兜孔几何参数对兜孔摩擦生热的影响Fig.8 Effect of pocket geometry parameters on frictional heat generation of pocket under different loads
由图8可知:随着载荷的增加,兜孔摩擦功耗先逐渐上升,而后趋于平缓。其原因是径向载荷较小时,滚子与兜孔间的打滑严重,滑动摩擦较大;当径向载荷进一步增大,保持架稳定性升高,打滑现象减轻,摩擦功耗相对减小。
图8(a)~图8(d)分别为在壁倾角α倾斜角度给定的情况下,在相同内圈转速、不同径向载荷的工况条件下,壁倾角β取不同值时兜孔的摩擦功耗。综合来看,兜孔摩擦生热趋势相近,但当壁倾角α保持不变时,β的变大导致滚子与兜孔的相对位置间隙变大,同时随着径向载荷的不断增大,滚子在高速旋转过程中与兜孔壁的碰撞频率和相互作用力升高,加剧了滚子与兜孔间的滑动摩擦,使得兜孔摩擦生热上升。壁倾角β保持不变时,α角的变大导致兜孔摩擦功耗升高,是因为壁倾角α的增大很大程度上造成滚子在周向平面上的窜动,且高速旋转过程中产生的离心力[17]引起滚子弹性滞后,导致滚子与兜孔间的接触力变大,从而对兜孔摩擦生热影响较大。
转速为24 000 r/min时,在相同载荷、不同兜孔几何参数的情况下,兜孔摩擦功耗的极差达到了736.2 W。
2.3 V形兜孔几何参数优化
因其具有均匀分布和齐整可比性的特点,正交试验法多用于研究多水平、多因素优化问题。因此,此处可有效用于轴承结构参数优化设计[18]。
笔者以兜孔摩擦功耗为目标参数,以兜孔壁倾斜角度为影响因素,对V形兜孔几何参数进行优化,以确定V形兜孔最佳壁面倾斜角度。由于轴承的径向载荷和转速会影响兜孔的摩擦功耗,在进行兜孔几何参数优化时,笔者仅考虑高速、轻载及临界载荷下,不同兜孔壁倾角组合对兜孔摩擦功耗的影响。

在兜孔壁倾角优化设计范围内,笔者均匀选取4个水平进行正交试验分析。
各因素及水平如表4所示。
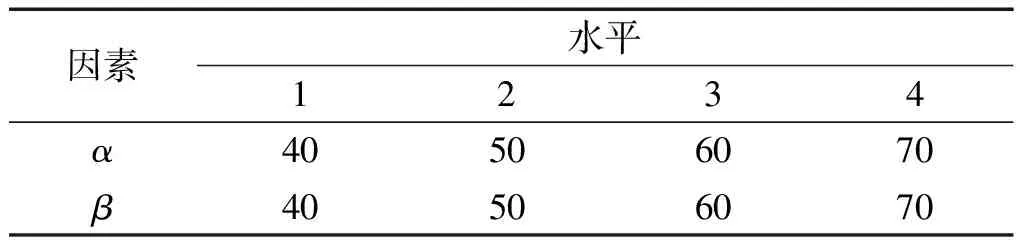
表4 正交试验因素水平表
高速、轻载工况下正交试验表L16(42)如表5所示。

表5 正交试验组合一及结果
表5为轻载100 N、转速24 000 r/min工况下,兜孔壁倾角正交试验组合及结果。
由表5可知:在兜孔壁倾角α、β的取值范围内,当α为40°、70°,β为40°、50°、70°时,兜孔摩擦功耗较低。
高速临界载荷工况下正交试验表L16(42)如表6所示。
表6为临界载荷900 N、转速24 000 r/min工况下,兜孔壁倾角正交试验组合及结果。
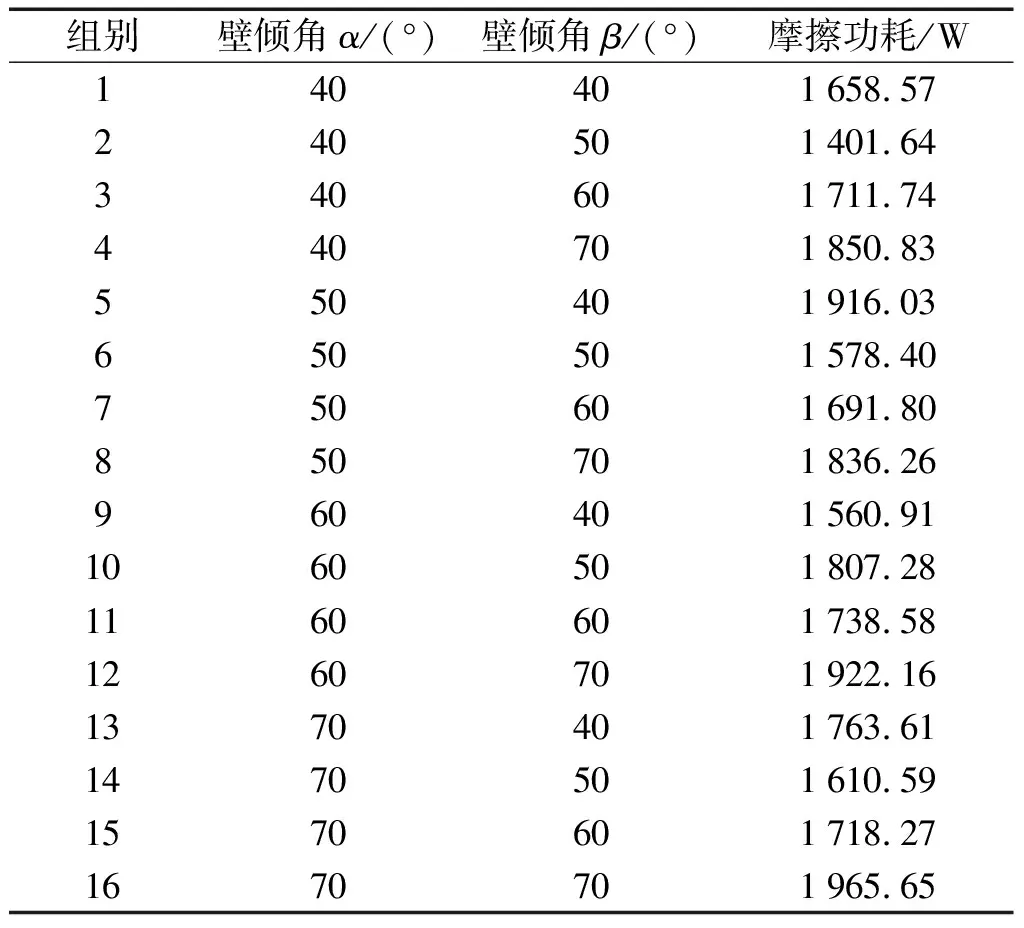
表6 正交试验组合二及结果
由表6可知:相较于表5,载荷的增大使得兜孔摩擦功耗变大;但在兜孔壁倾角α、β的取值范围内,仅当兜孔壁倾角取值较小时,兜孔摩擦功耗相对较低。
笔者把各正交试验组合的结果转化为三维曲面图,进行直观对比分析,如图9所示。
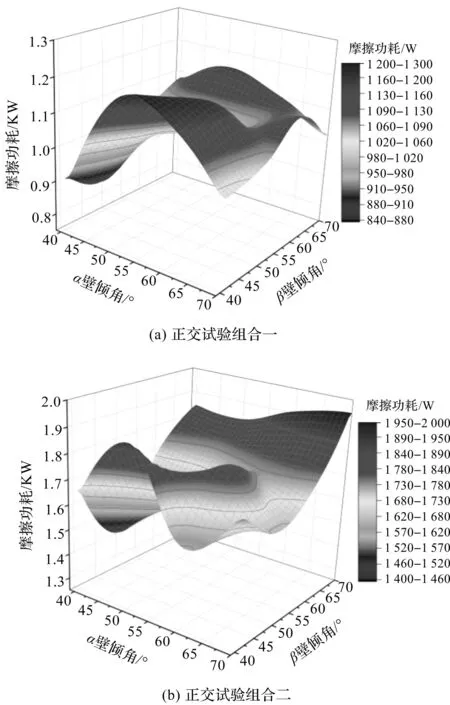
图9 正交试验三维曲面图Fig.9 Orthogonal test three-dimensional surface diagram
由图9可知:V形兜孔壁倾角的改变导致相同工况下兜孔摩擦功耗的差异较大。当壁倾角40°≤α<45°,45°≤β<55°时,兜孔摩擦功耗相对较小,因此综合考虑兜孔摩擦生热结果和轴承可制造性,笔者将α=40°、β=50°作为优化后的V形兜孔壁倾斜角度。
3 优化轴承摩擦生热特性
为探讨V形兜孔几何参数优化后轴承的摩擦生热特性,笔者对比分析了优化后的V形兜孔轴承与普通圆弧兜孔轴承在高速、轻载工况下的摩擦生热结果。
不同转速下,优化后的V形兜孔轴承与普通圆弧兜孔轴承摩擦生热结果如图10所示。
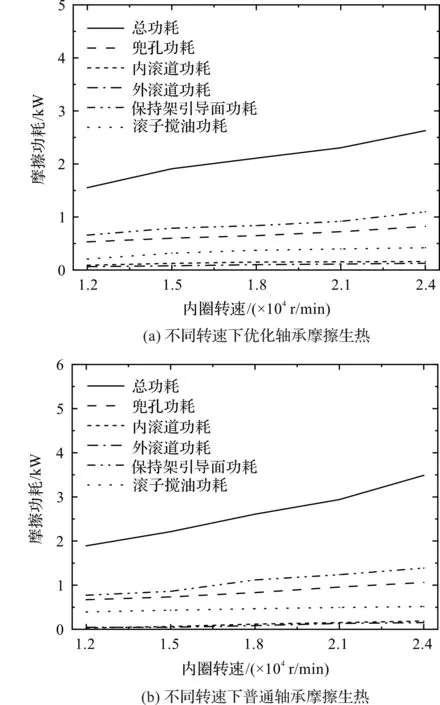
图10 不同转速下轴承摩擦生热对比Fig.10 Comparison of bearing frictional heat generation at different speeds
由图10可知:在径向载荷100 N、转速范围为12 000 r/min~24 000 r/min的工况下,优化轴承摩擦生热的结果比普通轴承摩擦生热的结果显著降低。
随着内圈转速的增加,滚子与滚道的摩擦功耗增幅较小,滚子的搅油摩擦功耗、保持架与套圈引导面的摩擦功耗和滚子与兜孔的摩擦功耗增幅较大。
优化轴承兜孔摩擦功耗和总摩擦功耗均低于普通轴承的功耗。
不同径向载荷下,优化后的V形兜孔轴承与普通圆弧兜孔轴承摩擦生热结果,如图11所示。

图11 不同径向载荷下轴承摩擦生热对比Fig.11 Comparison of bearing frictional heat generation under different loads
由图11可知:在转速24 000 r/min、径向载荷范围为100 N~900 N的工况下,优化轴承与普通轴承摩擦生热的趋势都是先上升而后趋于平缓,然而优化轴承摩擦生热的结果仍较普通轴承摩擦生热的结果低。
在高转速下,径向载荷的增加使轴承各部件间的稳定性升高,减少了滑动摩擦,因此轴承摩擦功耗随着径向载荷的增加先上升然后趋于平缓。但随着径向载荷的增加,优化轴承各部件间的运动关系达到平衡状态的速度较快,降低了各部件间的摩擦生热。
优化轴承与普通轴承在不同工况下,滚子与兜孔壁面接触力随时间变化图,如图12所示。
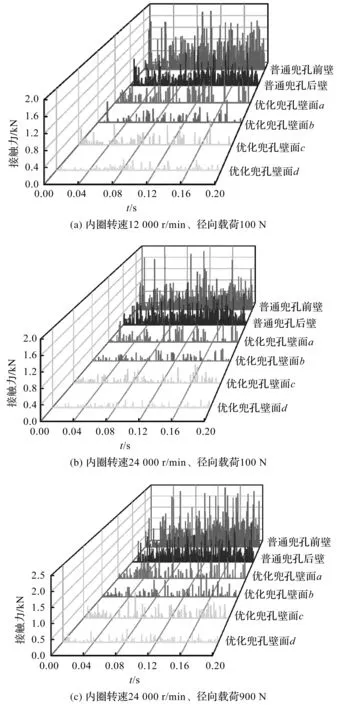
图12 不同工况下优化轴承与普通轴承滚子与兜孔接触力对比Fig.12 Comparison of contact forces between optimized bearings and ordinary bearings under different working conditions
由图12(a)和图12(b)可知:随着内圈转速的升高,滚子与兜孔壁面碰撞频率升高,导致轴承稳定性降低。但因V形兜孔结构对滚子有较好的径向定位,改善了滚子和兜孔的接触状态,使得优化轴承滚子与兜孔壁面的接触力明显低于普通轴承的接触力,提高了优化轴承在高速运转时的稳定性,遏制了转动过程中各部件间的滑动摩擦,从而降低了轴承各部件间的摩擦生热。
图12(b)和图12(c)则表明了径向载荷的增加使滚子与兜孔壁面的接触力增大。
然而普通轴承的稳定性低于优化轴承的稳定性,兜孔各壁面与滚子的碰撞频率明显高于优化轴承。所以优化轴承在运转时,滚子的自转速度和保持架转速相较于普通轴承能更快达到稳定状态,减少了不平衡状态下滚子与兜孔的滑动摩擦生热。同时优化轴承较高的稳定性也使得各部件间的摩擦生热均低于普通轴承。
兜孔结构的改变势必会导致保持架稳定性的改变,因此,笔者利用保持架打滑率[19]来评判优化轴承的稳定性。
优化轴承与普通轴承保持架打滑率变化趋势,如图13所示。
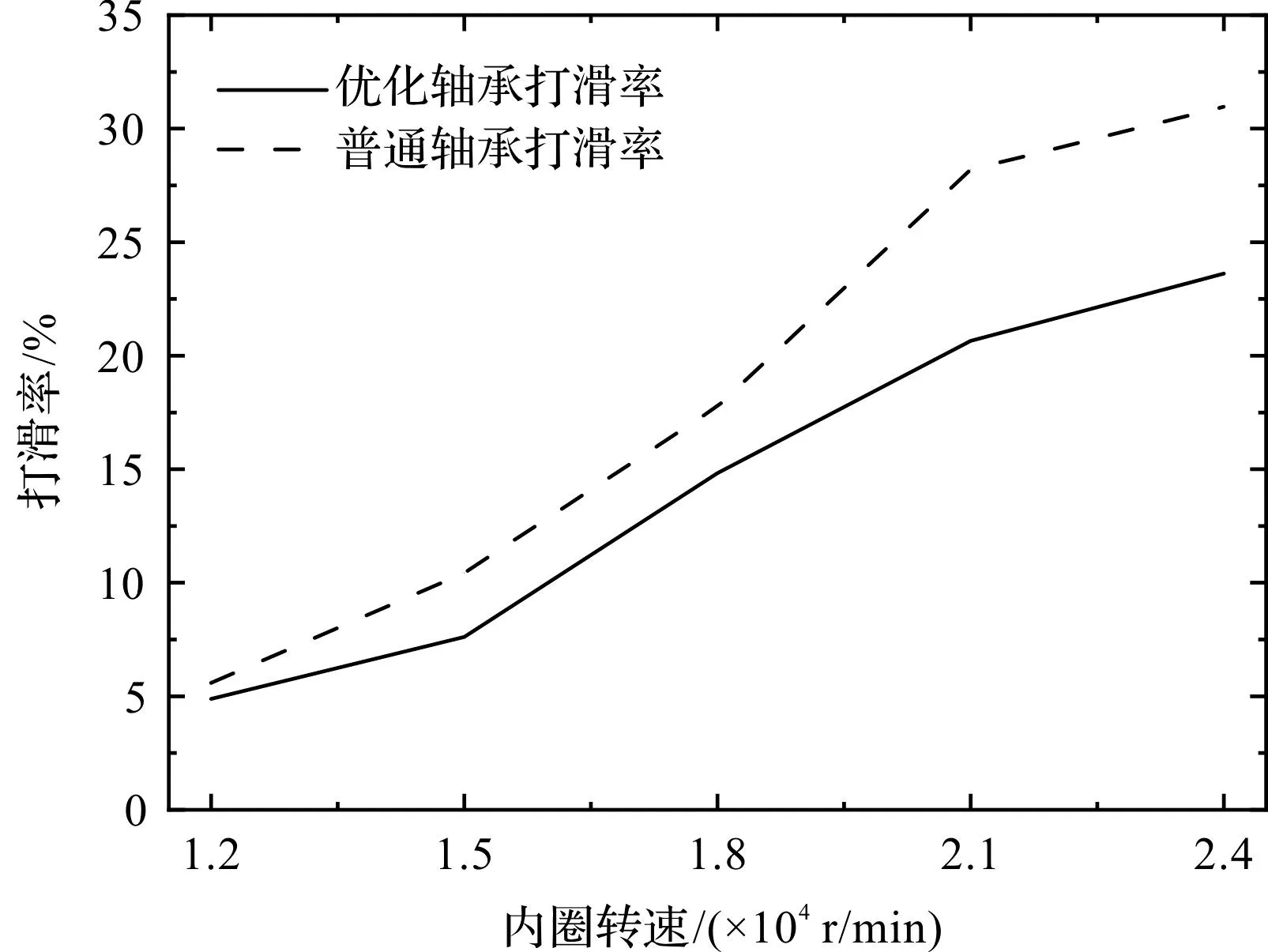
图13 不同转速下保持架打滑率对比Fig.13 Comparison of cage slip rate at different speeds
由图13可知:当径向载荷为100 N、转速范围为12 000 r/min~24 000 r/min时,优化轴承的保持架打滑率均低于普通轴承的打滑率,稳定性优于普通轴承。
这是因为轴承工作时打滑造成的问题主要有油膜破裂后,在轴承滚子和套圈滚道的接触区域发生刚性接触引起的热损伤,这将会导致温度急剧上升,并迅速传递至轴承各部件接触区域[20];但优化轴承打滑率较低,避免了轴承因打滑导致部件温度升高进而发生结构变形,使各部件接触位置摩擦生热加剧。
4 结束语
针对V形兜孔圆柱滚子轴承的兜孔几何参数影响轴承摩擦生热特性的问题,笔者以V形兜孔圆柱滚子轴承为研究对象,结合轴承动力学和摩擦功耗模型,考虑了高速轻载工况下不同兜孔几何参数对滚子与兜孔摩擦生热的影响,采用正交试验法优化了V形兜孔壁倾斜角度,分析了兜孔几何参数优化轴承与普通轴承各部件摩擦生热及总摩擦生热的差异。
研究结论如下:
1)V形兜孔的壁面倾斜角度对滚子与兜孔间的摩擦生热影响较大,不同的兜孔壁倾角组合导致兜孔摩擦生热的升高趋势不同,且在同一工况下兜孔摩擦功耗的最大差值达到了736.2 W;
2)在给定工况下,且在兜孔壁倾角40°≤α≤70°、40°≤β≤70°的取值范围内,相较于其他兜孔壁倾角组合,壁倾角α=40°、β=50°时,能有效减少兜孔摩擦生热;
3)V形兜孔几何参数优化后,优化轴承内部各热源摩擦生热和轴承总摩擦生热均低于普通轴承的摩擦生热,优化轴承滚子与兜孔的接触力较低,且滚子与兜孔的碰撞频率和保持架打滑率均优于普通轴承。
后续工作中,笔者将进行轴承实际工况下的温升试验,利用温度传感器测量优化轴承和普通兜孔轴承的工作温度,并将二者的温度进行对比,以间接验证优化轴承实际工作中产生的摩擦热是否优于普通轴承的摩擦生热。

