基于频率成比例重分配线性Chirplet变换的时频分析方法*
岳子毫,裴 帮,王征兵,李志远,雷欢欢
(郑州机械研究所有限公司,河南 郑州 450001)
0 引 言
齿轮箱是传动系统中的一个重要部件,广泛应用于各个领域,其性能直接影响整个设备的健康状态。因此,齿轮箱的状态监测和故障研究对保证机械设备的安全稳定运行具有重要意义[1]。
目前,振动分析是齿轮箱状态检测与故障诊断中应用最广泛和最有效的方法[2]。齿轮箱在运行时受到转速和负载变换的影响,因此,其所收集到的振动信号是非平稳的,且信号分量的振幅和频率随时间变换。时频分析方法是目前处理非平稳信号的最有效的方法之一,其已经在工程上得到了广泛的应用[3-5]。
时频分析可以将一维时域信号映射至二维时频域中,再从时频域中提取非平稳信号的时变幅度和频率特性。传统的时频分析方法(如短时傅里叶变换和小波变换)是利用计算信号与时频基之间的内积,从而得到信号中的瞬时特征[6];但是受到海森堡不确定原理的影响,其所得到的时域分辨率和频域分辨率不能同时达到最佳。Wigner-Ville分布采用双线性积分变换,其可以获得更高的时频域联合分辨率;但是存在交叉项的干扰问题[7]。
传统的各类时频分析方法存在各自的限制问题。因此,为获得更好的时频域表示,近些年许多学者在此方面进行了研究,并提出了大量有效的方法。
根据内积定理,基函数与信号的非平稳特征越匹配,得到的时频表示集中度也越高。MANN S等人[8]提出了Chirplet变换,使用参数Chirprate获得线性Chirplet基,以此来匹配信号的瞬时频率特征,相较于传统的时频分析方法,其能够获得更好的时频表示;但是Chirplet变换的线性调频基只能匹配线性瞬时频率。由Weierstrass逼近定理可知,非线性函数可以被足够阶的多项式近似。为了处理非线性信号,PENG Zhi-ke的团队[9-10]提出了多项式Chirplet变换,通过构造多项式基来匹配信号的非线性瞬时频率;但是其在处理多分量信号时,不能使多项式基与所有分量匹配,且多项式阶数直接影响计算的复杂度,需要权衡匹配精度和计算复杂度的关系。为了解决这个问题,YANG Yang等人[11-12]又提出了样条Chirplet变换、广义莺变换;但是这些方法不能同时匹配所有分量的瞬时频率。
YU Gang等人[13]提出了一般线性Chirplet变换(general linear Chirplet transform, GLCT)方法,通过融合多个Chirplet变换产生的结果中能量聚集度的部分来获得时频表示,所得到结果的能量聚集度高于任何单个Chirplet变换的结果;但是GLCT在处理瞬时频率轨迹间隔较小的信号时,分离能力较差[14]。
以上方法都采用了固定的窗口长度,从而导致只能得到固定的分辨率。GUAN Peng-fei等人[15]提出速度同步线性Chirplet变换(velocity synchronous linear Chirplet transform,VSLCT),即通过构造一组与轴速度同步的线性Chirplet基函数,以此来匹配瞬时频率的轨迹,构造了非正交基,并考虑了时变窗口,其可以清楚地表征所有轴速同步频率分量;但是该方法计算复杂度大,且时频表示会出现中断现象。
时频方法在处理信号所得到的时频域表示时,存在拖尾现象。因此,为了提高时频聚集度,一些学者提出了一些后处理方法。
AUGER F等人[16]提出了重新分配方法(reassignm-ent method, RM),将时频分布从原始位置重新分配到局部范围谱的质心,从而提高时频聚集度;然而RM的过程是不可逆的,不能实现信号重建目的。在RM的基础上,DAUBECHIES I等人[17]提出了同步挤压小波变换(synchronous squeezing wavelet transform, SST),其可以较好地完成信号的重建工作。随后,OBELIN T等人[18]提出了SST的傅里叶变换版本(Fourier-based synchro squeezing transform,FSST),在重新分配过程中,SST会将噪声引入时频结果。YU Gang等人[19]提出了同步提取变换(synchronous extraction transfor-mation,SET),利用狄拉克函数和估算频率构建了同步提取算子,只提取与瞬时频率最相关的成分,避免了噪声的干扰,相较于SST,其能获得更高的时频聚集度。
然而,以上这些方法在处理强时变信号和高噪声信号时的效果并不理想。
为了对齿轮进行故障诊断,同时针对上述问题,笔者从齿轮故障振动信号的调制现象出发,讨论基函数对时变信号分析的影响,提出一种时频方法-频率成比例重分配Chirplet变换(PFSRLCT)方法,并分别在模拟信号和实际齿轮故障信号上对PFSRLCT方法进行验证。
1 齿轮故障信号调制现象
齿轮在正常工况下啮合时,其振动信号由齿轮的啮合频率及其谐波组成,即:
(1)
式中:Ai为i阶谐波的幅值;fm为齿轮啮合频率;φi为i阶谐波的相位。
齿轮啮合传动中,负载、刚度和转速的变化以及故障的发生,都会使得齿轮振动信号产生调制现象。由此,齿轮的振动信号可以表示为:
(2)
式中:ai(t)为调幅函数;bi(t)为调频函数。
齿轮故障信号产生调幅调频现象时,时域和频域如图1所示。

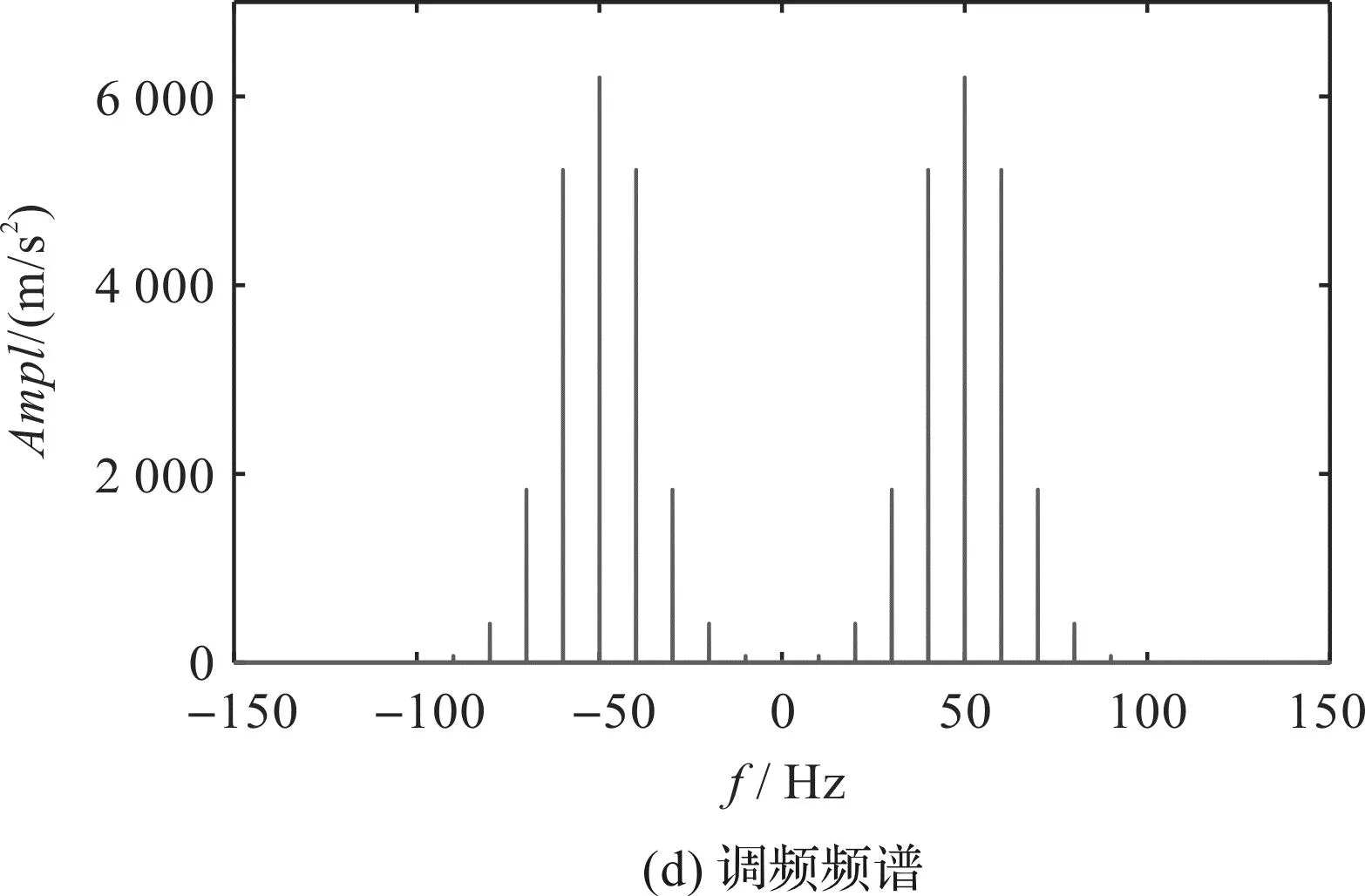
图1 齿轮故障信号的调幅调频现象Fig.1 Amplitude modulation and frequency modulation of gear fault signal
对于齿轮振动信号,啮合频率为载波频率fm,齿轮的旋转频率为调制频率fr。当齿轮发生断齿等局部故障时,振动信号会被调幅,在频谱上产生以载波频率与调制频率的和频及差频。如果调制信号不是单一信号,而是具有谐波成分的信号,则会在载波频率及其谐波两侧出现以调制频率为间隔的一系列边频带。局部故障还会产生调频现象,在频谱上会产生以载波频率为中心,以调制频率为间隔,对称分布的无限多对的边带。在实际的齿轮系统中,调幅和调频一般同时存在。
调幅调频现象同时存在时,振动信号的频谱如图2所示。
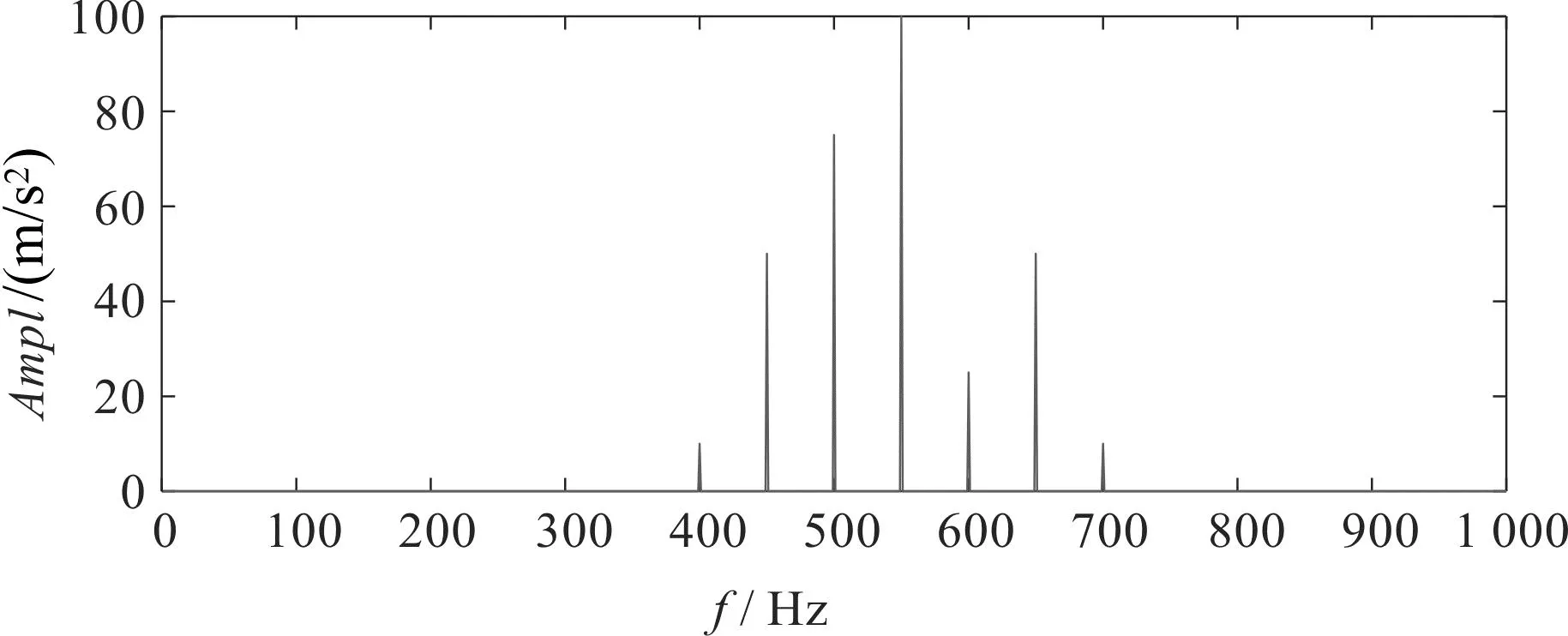
图2 调幅调频同时存在的信号频谱Fig.2 Signal frequency spectrum when AM and FM exist at the same time
由于边频成分相位的不同,矢量相加后会在频谱上形成复杂的不对称调制边带。同时,齿轮的旋转频率与载波频率存在以下关系:
fr=fm/Z
(3)
式中:Z为齿轮齿数。
由上述分析可知,齿轮振动信号中各个频率分量的频率成比例。
2 Chirplet变换
信号x(u)òL2(R)的Chirplet变换可以表示为:

(4)
式中:A(u)为信号x(u)的Hilbert变换,表示为s(u)=x(u)+jH[x(u)];g(t)为窗口函数,通常采用高斯函数g(t)=exp(-t2/(2σ2)),其中σ为高斯窗口参数;φ(f,u,tc)为相位函数。
φ(f,u,tc)可表示为:
φ(f,u,tc)=C(u-tc)2/2
(5)
式中:C为Chirprate。
Chirplet变换本质上是一种加窗变换,在时间窗口内通过旋转Chirplet,使得其与瞬时频率轨迹匹配,以此来获得更高的时频能量聚集度。
与短时傅里叶变换(short time Fourier transform,STFT)相比,其不同在于Chirplet变换利用Chirplet基与瞬时频率轨迹匹配,而不是时频基。时频能量聚集度和Chirplet与瞬时频率轨迹重合程度成正比,当Chirplet与瞬时频率轨迹完全重合时,应该存在Chirplet旋转角θ的正切值等于目标瞬时频率的轨迹的斜率。
Chirplet的旋转角度可以表示为:
φ′(f,u,tc)=dφ/du=C(u-tc)
(6)
-tan(θ)=dφ′/du=C
(7)
观察式(4)可以得出,当C=0,Chirplet变换退化为短时傅里叶变换。
Chirplet变换相较于短时傅里叶变换能量聚集度更高的原因如图3所示。
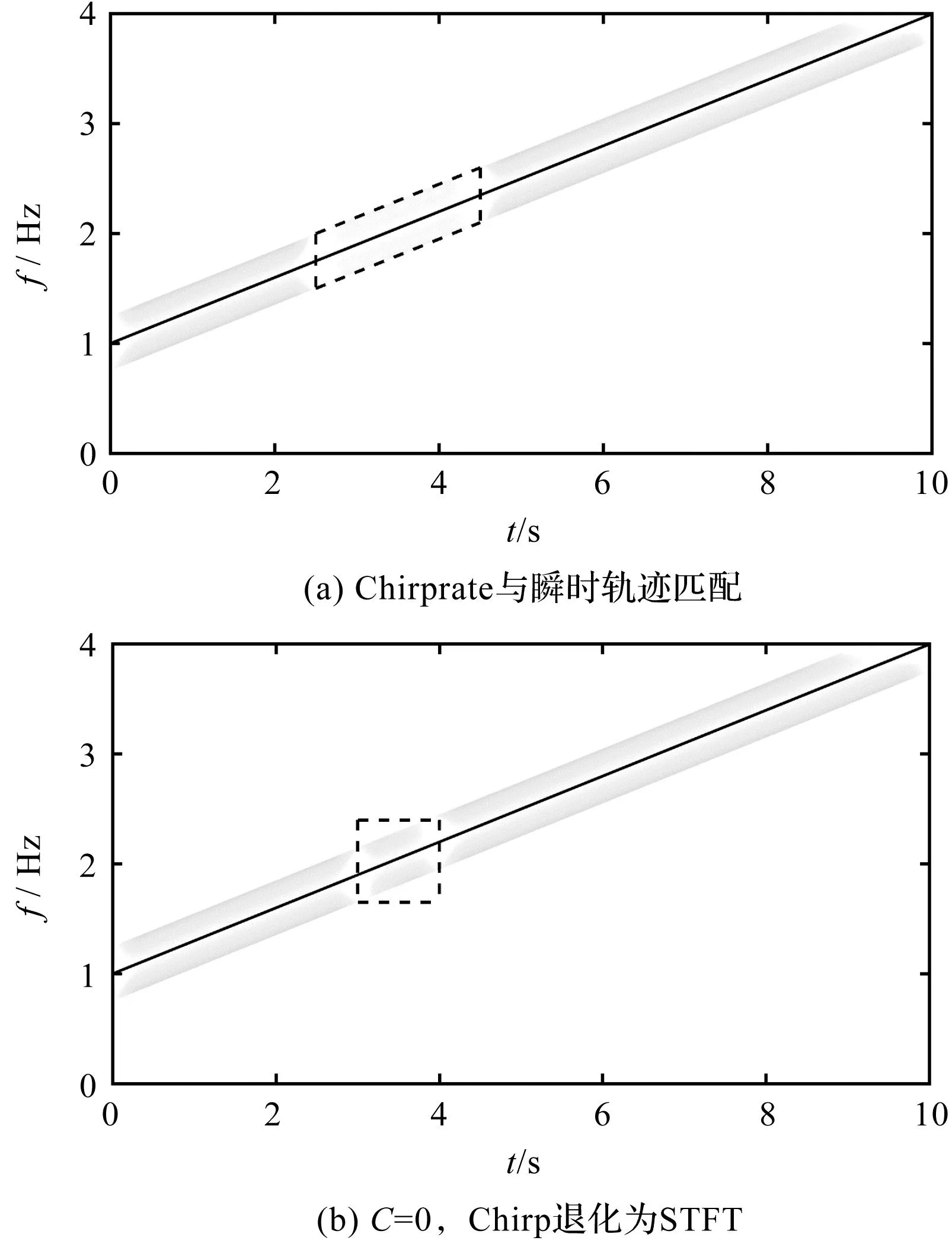
图3 Chirprate对时频聚集度的影响Fig.3 The influence of CR on TF energy concentration degree
由图3可知:短时傅里叶变换的时频基与瞬时频率轨迹仅在时间窗口宽度中心处匹配,在窗口的其他位置与真实时频特征不匹配,能量分布较为分散。
笔者对单分量非平稳信号进行Chirplet变化时,Chirplet基瞬时频率轨迹匹配如图4所示。
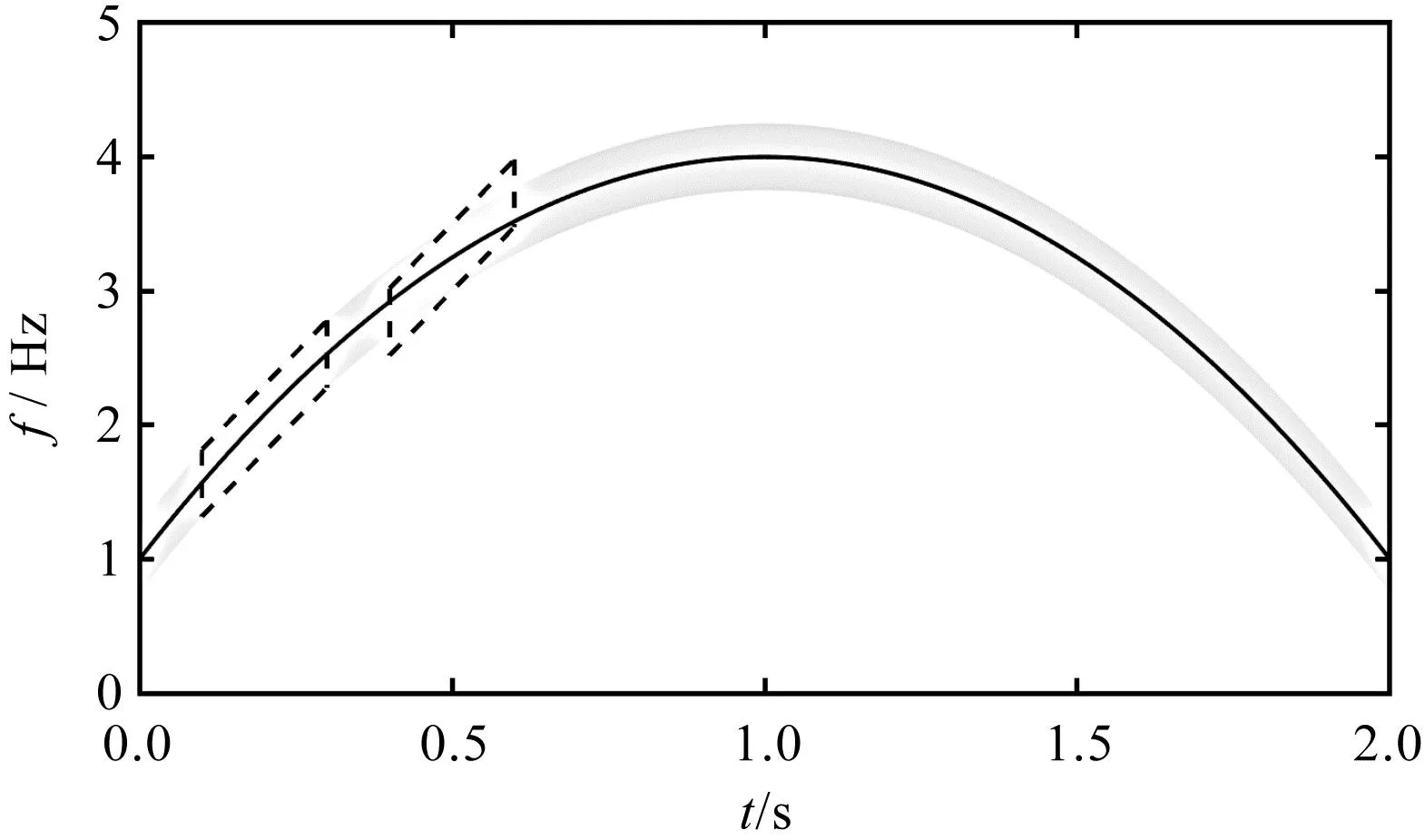
图4 单分量信号的Chirplet变换Fig.4 Chirplet transform of single component signal
由图4可知:当所考虑的信号包括时变频率分量时,任何单个Chirplet变换都不能与瞬时频率轨迹完美匹配。
针对上述问题,YU Gang提出了GLCT,即在每个时间窗口内寻找与该时间窗口内瞬时频率轨迹匹配的Chirprate,结合多个Chirplet变换的结果,引入参数α,其公式如下:
(8)
式(4)改写为:
(9)
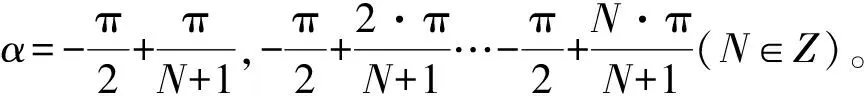
当N=1时,GLCT退化为Chirplet变换。
GLCT有效地解决了瞬时频率轨迹斜率随时间变换的问题。笔者采用时变Chirplet匹配频率轨迹,在处理单分量信号时可以获得良好的能量聚集度。
GLCT处理多分量非平稳信号如图5所示。
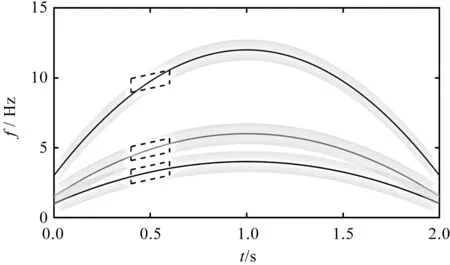
图5 多分量信号的GLCTFig.5 GLCT transform of multi-component signal
由图5可知:当处理多分量信号时,如齿轮箱瞬时频率成比例的多分量信号,在每个时间窗内的各个分量信号的瞬时频率具有不同的斜率,GLCT不能完全匹配所有的分量信号。此外,GLCT不适合处理频率间隔较近的多分量信号。
3 频率成比例重分配线性Chirplet变换
为了解决时频分析存在的问题,笔者提出了频率成比例重分配线性Chirplet变换(PFSRLCT)方法。
首先,替换Chirplet变换的核函数,得到成比例频率线性Chirplet变换(proportional frequency linear Chirplet transform,PFLCT);然后,提取时频脊,获得同步重分配算子(synchronous reassignment operator,SRO),对时频结果进行了同步分配,进一步提高了能量集中度。
3.1 成比例频率线性Chirplet变换
修改式的相位函数为:
φ(f,u,tc)=fC(u-tc)2/2
(10)
式中:f为频率。
由此,式(4)改写成:
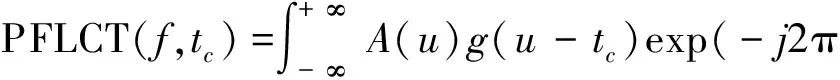
(11)
由Ville理论[20]和泰勒公式可得:
(12)
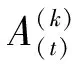

f(u)=f(tc)+f′(tc)(u-tc)
(13)
将式(12)和式(13)代入式(11),可得:
|PFLCT(f,tc)|=
g(u)exp(-j2πf(tc)Cu2)exp(-jωu)du|=
exp(-j(ω-2πf(tc))u)du|
(14)
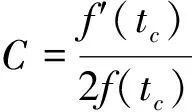
(15)
由上式可知,当C满足C=f′(tc)/2f(tc)时,ω在2πf(tc)处|PFLCT(f,tc)|取得最大值,即获得最高能量浓度。由此可以证明,PFLCT可以处理具有瞬时频率成比例的信号。
另外,PFLCT还可用于处理具有瞬时频率成比例的多分量信号,证明过程如下:
假设多分量信号f(t)=f1(t)+f2(t)且∃f1(t)=af2(t),那么对于信号f(t)进行PFLCT变化可得:

(16)
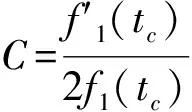

(17)
由式(17)可证PFLCT可用于分析具有成比例瞬时频率的多分量信号。
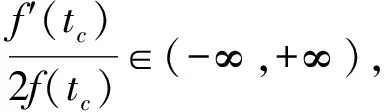
(18)
式中:N为从-π/2到π/2的整个角度跨度中的段数。
即对于∀tc,∃tanαk=f′(tc)/2f(tc),k∈[1,N],当时间窗口内时频基与瞬时频率轨迹最匹配时,时频域的能量集中在各分量的对应频率上,这时时频域的峭值达到最大值。
因此,可以使用峭值作为指标来确定C的值:
(19)
式(18)中,N的值越大,式(19)中C的值越精确,时频基和瞬时频率轨迹匹配程度越良好;但是过大的N值会增加计算负担。
笔者在该项研究中设置N为50。
PFLCT的算法流程如下:

算法1:PFLCT输入A(u),σ,fs,Nfor i=1:NTFRs(t,f,i)=∫+∞-∞ A(u)g(u-t)exp(-jω(u-t))exp(-j2πftan-π2+iN+1π()(u-t)2)duend forCI=Kurtosis(TFRs,t)Index=argmaxc(CI)TFR=TFRs(index)输出TFR,index,t,f
3.2 同步重分配
对于多分量信号,其中每个分量信号的瞬时频率应该有足够的间隔,才能从时频域中提取出各分量时频脊线,即:
|fi(t)-fi+1(t)|>2Δ
(20)
式中:fi(t)为第i个分量信号的频率,i∈Z;Δ为固定频率间隔。
目前,已经有了大量的研究来解决时频脊线提取的问题。THAKUR G等人[21]开发了与式(20)的分辨率相关的另一种简单而有效的方法,其表达式如下:

(21)
式中:(t,φk(t))为时频域内的估计瞬时频率轨迹;λ,β为曲线平滑度和能量最大化的权衡参数。
该方法采用贪婪算法寻找局部最优解,其具体步骤为:
1)将时频信号按时间方向分割为若干片段,并确定每个片段的搜索起点;
2)以最大化式为衡量标准,使用向前向后的方式搜索瞬时频率脊线;
3)每获取完整的一条瞬时频率脊线后,在原信号去除该分量;
4)重复步骤1)~步骤3),直到提取出所有瞬时频率脊线。
寻找时频脊线的算法流程如下:

算法2:寻找时频脊线输入TFR,N,β,M,N[flen tlen]=size(TFR)for i=1:Mfor k=1:NIF(tk)=argmaxf(TFR(k·tlen/(N+1),f))IF(tk-1)=argmaxf(TFR(k·tlen/(N+1)-1,f))for j=k+1:tlenIF(tj)=argmaxf∈[IF(tk-1)-Δ,IF(tk-1)+Δ](|TFR(f,tj)|2-β(f-2IF(tj-1)+IF(tj-2))2)end forfor j=0:k+1IF(tj)=argmaxf∈[IF(tk+1)-Δ,IF(tk+1)+Δ](|TFR(f,tj)|2-β(f-2IF(tj+1)+IF(tj+2))2)end forend forIFs(:,M)=IFTFR(t,(IF(t)-Δ,IF(t)+Δ))=0clear IFend for输出IFs
笔者利用提取到的各分量的时频脊线和狄拉克函数,使得时频能量仅在瞬时频率轨迹处分布。
因此,可得到同步分配算子SRO如下:
(22)
式中:IF(t)为时频脊线。
PFSRLCT可以表示为:
PFSRLCT(f,t)=PFLCT(f,t)·SRO(f,t)
(23)
重分配过程是仅将每条时频脊线上的局部最大时频幅值重新分配给新的时频域表示。因此,重分配后的时频域表示具有更高的时频聚集度。
笔者对时频结果进行重分配的算法流程如下:

算法3:重分配TFR输入TFR,IF,M,Δkk=1:hlength:hlength·llengthindex=kk+IF-1;SRO=zeros(size(TFR))for i=1:Mindex1=repmat(index,Δ+1,1)+linspace-Δ2,Δ2,Δ+1()TSRO(index1)=1end forTFR=TFR.∗SRO输出TFR
4 模拟信号验证
笔者使用模拟信号来验证PFSRLCT的有效性,并将其与其他方法进行了对比。
非线性多分量模拟信号模型如下:
(24)
该多分量信号包括3个瞬时频率成比例的非线性信号,采样频率为1 000 Hz,采样时长为3.5 s,笔者设置信噪比SNR=-1 dB。
该多分量信号的信号波形如图6所示。
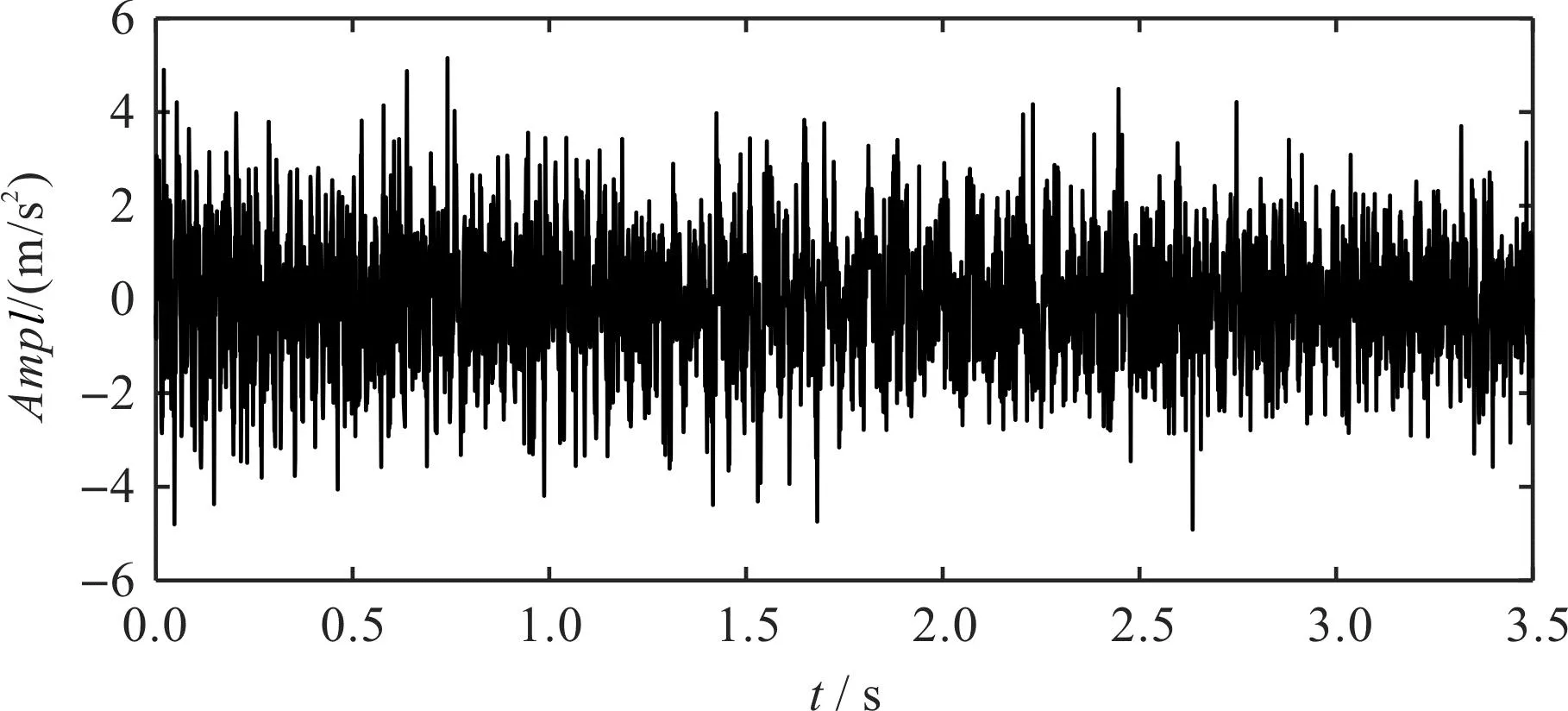
图6 模拟信号的时域波形Fig.6 Time domain waveform of analog signal
4.1 表现能力验证
笔者利用式(24)建立了模拟信号的分析结果,如图7所示。
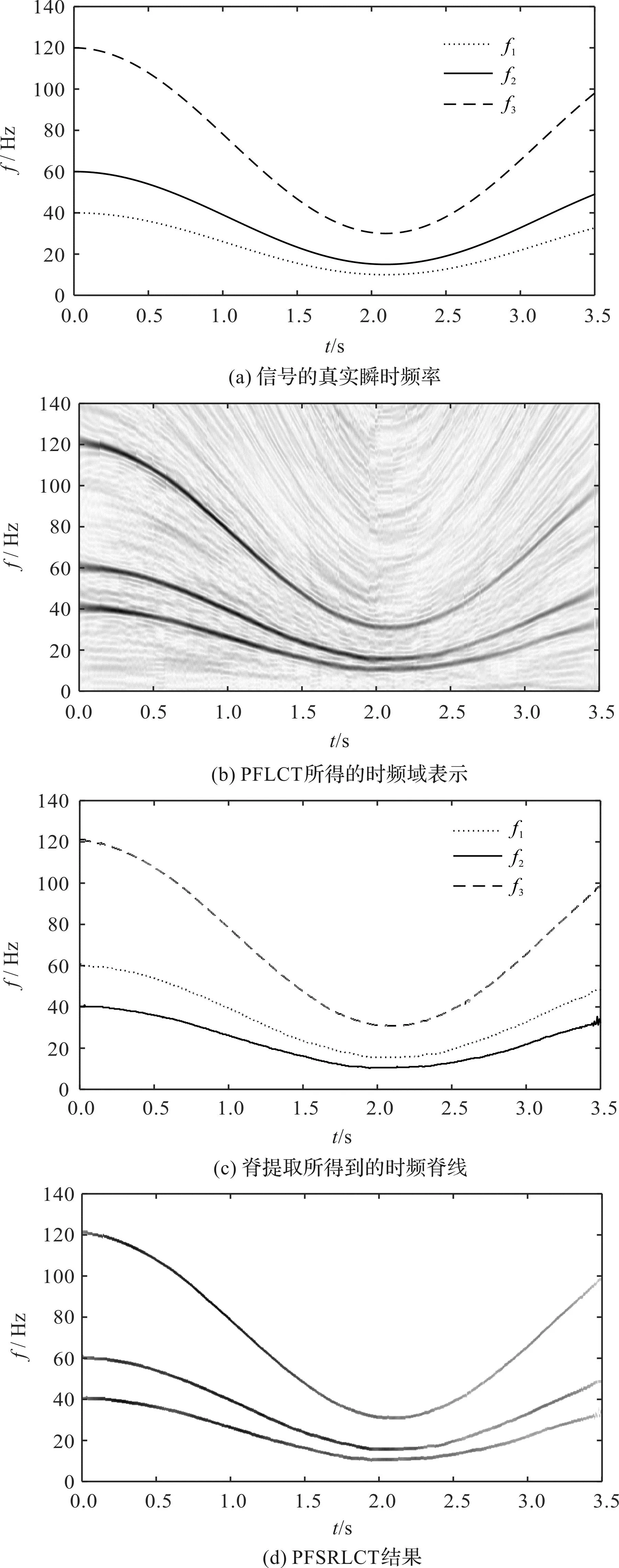
图7 模拟信号分析结果Fig.7 Analysis results of analog signals
图7(a)为信号的瞬时频率轨迹,图7(b)为应用PFLCT获得的时频域结果。对比两者结果可以发现:PFLCT得到的时频表示可以清楚地分辨出各个分量信号,证明该方法对于处理间隔紧密的瞬时频率成比例多分量信号具有良好的效果。
图7(c)为对PFLCT所得时频结果进行脊提取得到的各分量的瞬时频率,可以看出:图中所提取的瞬时频率轨迹与真实瞬时频率基本吻合;笔者利用所提取的时频脊线获得同步重分配算子SRO,对PFLCT进行重分配后所得时频域表示如图7(d)所示。由图7(b)中的时频结果比较可知,重分配后的时频结果能量更加集中。
为了评估PFSRLCT方法的表现能力,笔者采用了一些传统方法和先进方法STFT、GLCT、SET、VLSCT、SST、SST2进行了比较。其中,STFT、GLCT、SET、SST、SST2的窗宽均设置为0.5 s,VLSCT的Nwl设置为30。
所得结果如图8所示。
通过观察图8可知:STFT受到拖尾效应的影响,所得时频域表示较为模糊,时频集中度较低;GLCT在处理f1、f2间隔紧密的频率时,发生了频率交叉,难以分辨出频率轨迹;SET结果时频集中度高,但f3轨迹在2 s后发生了模糊;VLSCT的时频表现良好,但是在2.5 s和3 s之间发生了中断。
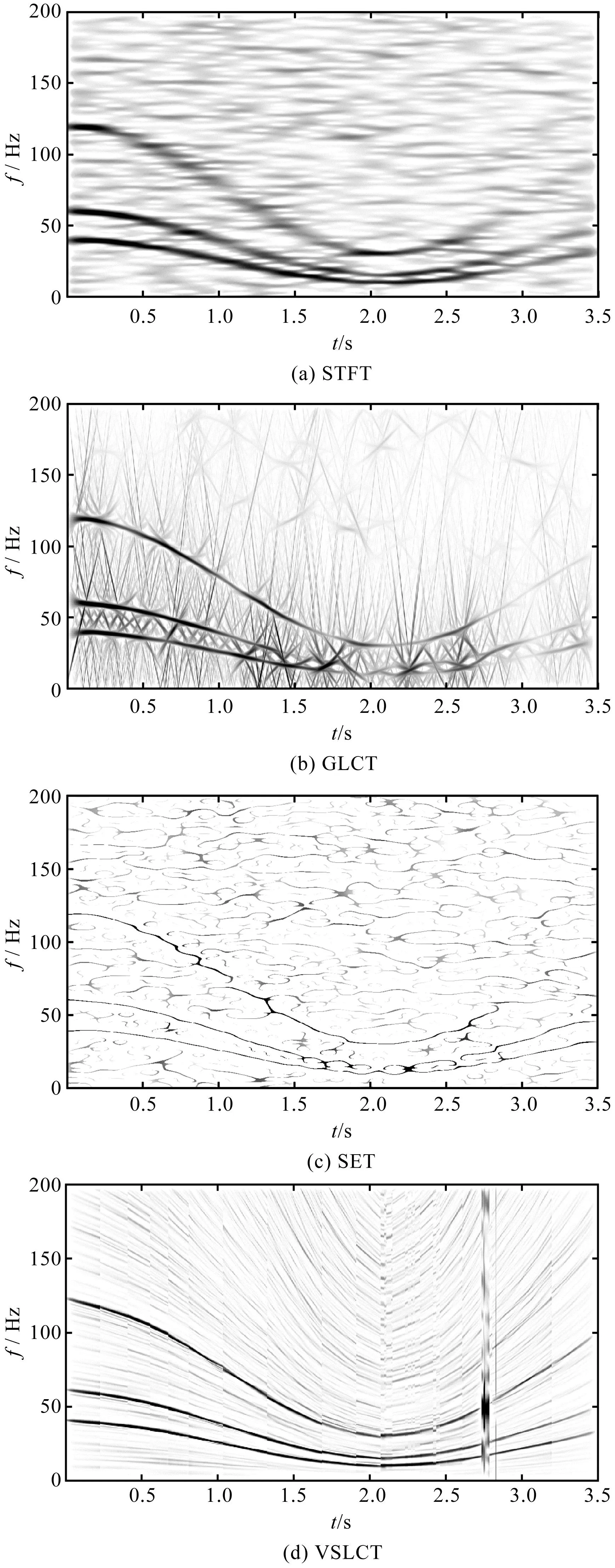

图8 各种时频方法的比较Fig.8 Comparison of various TFA methods
图8(e)、图8(f)分别为SST和SST2的结果,这两种方法相对于STFT有较好的时频集中度,但是在幅值上有所削弱,在频率间隔较近时仍有模糊。
为了验证PFSRLCT的抗噪性能,笔者引入了Rényi熵来衡量时频域的集中度。
Rényi熵由下式确定:
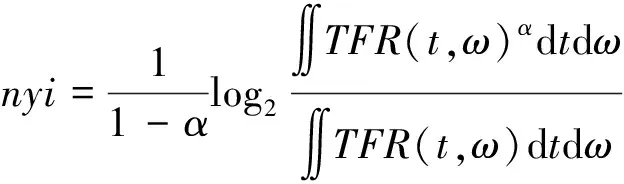
(25)
其中:α设置为3。
Rényi熵可以量化TFR的清晰度,Rényi熵越高意味着时频表示越模糊。
通过式(25)可计算得到各种时频方法的Rényi熵,如表1所示。
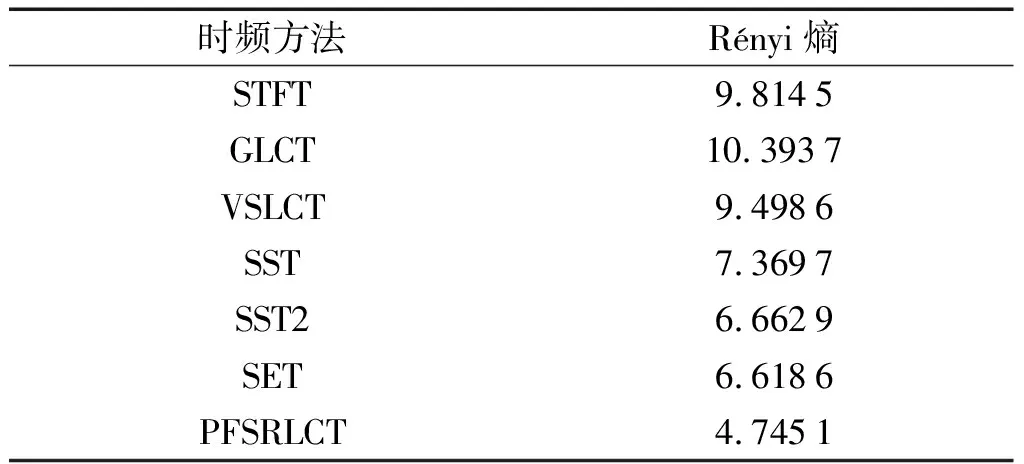
表1 各种方法的Rényi熵对比
由表1可知:GLCT得到时频结果的Rényi熵最大,为10.393 7;PFSRLCT所获得的Rényi熵最小,为4.745 1,并且明显低于其他时频方法。
由此可以证明,PFSRLCT所获得时频能量集中度最高,相对于其他时频方法有明显优势。
4.2 噪声鲁棒性
为了检测该方法对于噪声的鲁棒性,笔者将具有不同信噪比的高斯噪声添加到信号中,使用频率估计误差来量化频率估计的准确性。
频率估计误差表示如下:
(26)

在提取时频脊的过程中,笔者提取7条时频脊线,并通过人工选取与真实瞬时频率最符合的3条脊线;利用式(26),得到模拟信号在信噪比为-2 dB~10 dB时频率估计误差,并将其与STFT、SST、VSLCT结果进行对比。
4种方法的频率估计误差,如图9所示。
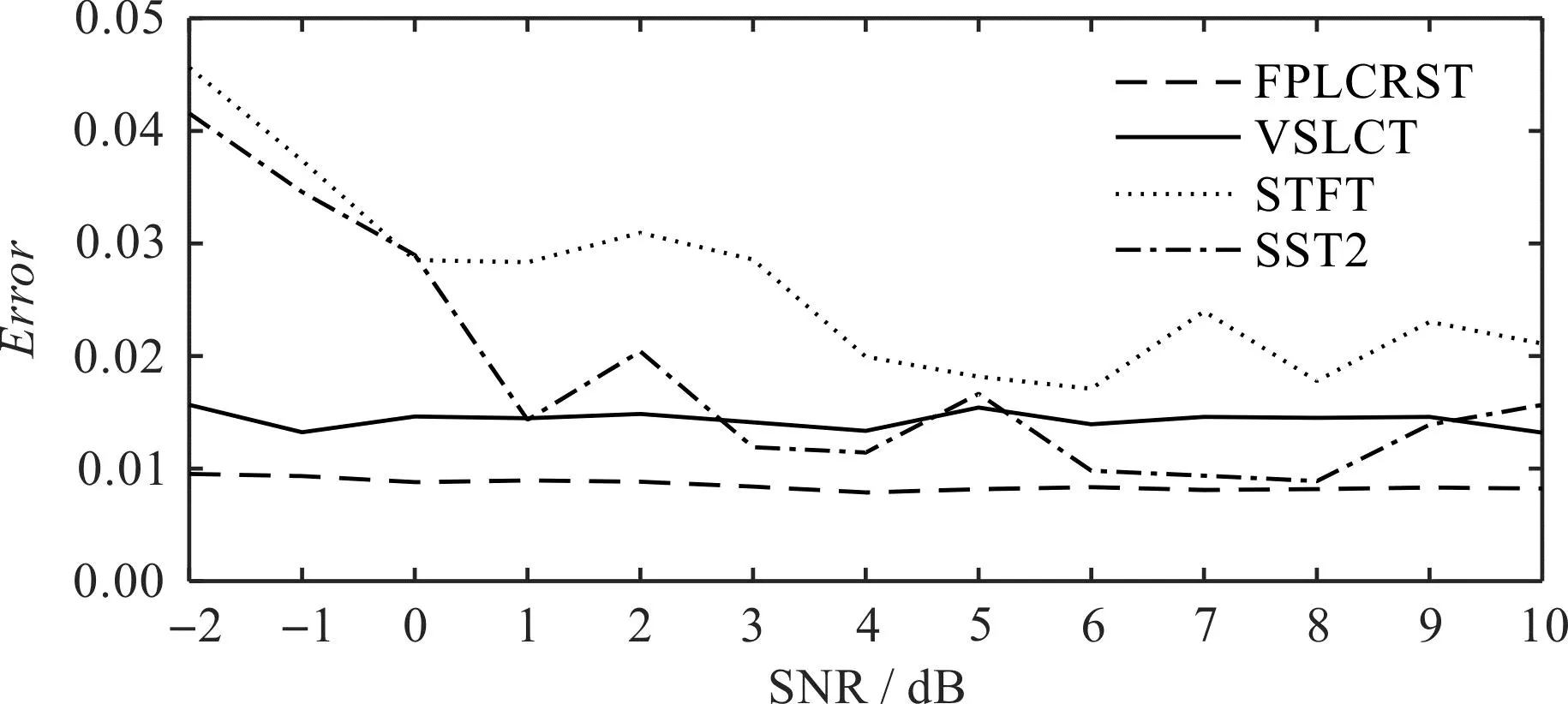
图9 频率估计误差对比Fig.9 Comparison of frequency estimation errors
从图9中可以看出:在信噪比较高时,SST2表现效果不佳,在信噪比高于1 dB时,表现效果与VSLCT相似,次于PFSRLCT的误差;由于STFT时频结果的能量局部带宽更大,干扰了脊提取算法,其结果的频率误差相对于其他3种算法最大,PFSRLCT所得到的频率估计误差最小,同时受信噪比的影响小。
在信噪比为-1 dB时,笔者采用4种方法得到了真实频率和估计频率,如图10所示。

图10 真实瞬时频率轨迹与估计瞬时频率轨迹的比较Fig.10 Comparison between real IF trajectory and estimated IF trajectory
由图10可以看出:PFSRLCT所得到的估计频率与真实频率符合度最高;VSLCT所得到的估计频率在2 s左右频率间隔较小处和2.5 s处有较大突变;STFT与SST2所得到的估计频率在2 s到2.5 s之间频率间隔较近处有较大误差,STFT所估计的f3受能量局部带宽影响较大,所得到的估计频率在真实频率上下浮动;受到噪声的影响,SST2所估计的f3在2.5 s后有较大的偏离。
5 地铁齿轮箱试验验证
笔者使用地铁齿轮箱试验平台收集振动信号,验证PFSRLCT方法处理实际信号的能力。
试验所采用的地铁齿轮箱为单级传动,其具体参数如表2所示。
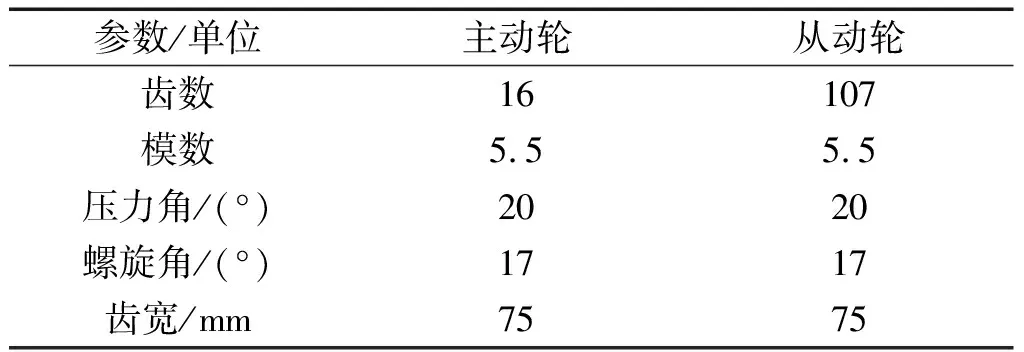
表2 齿轮箱参数
测点位置为输入端轴承座处。笔者设置齿轮箱的故障类型为断齿,采用线切割的方式将轮齿从齿根处切除。
齿轮箱及测点位置和试验现场如图11所示。

图11 试验条件Fig.11 Test conditions
在齿轮箱输入端,笔者以30 rad/s2的加速度从速度为0 rad/s开始进行恒加速,输入转矩为1 008 N·m;传感器采用加速度传感器,采样频率为10 240 Hz。
所采集的振动信号时域波形如图12所示。
图12 试验信号时域波形Fig.12 Time domain waveform of experimental signal
笔者采用PFSRLCT与STFT、GLCT、SET、VLSCT、SST、SST2方法进行比较分析,截取了0.18 s~0.21 s之间的时频表示。
PFSRLCT所得到的时频域表示如图13所示。
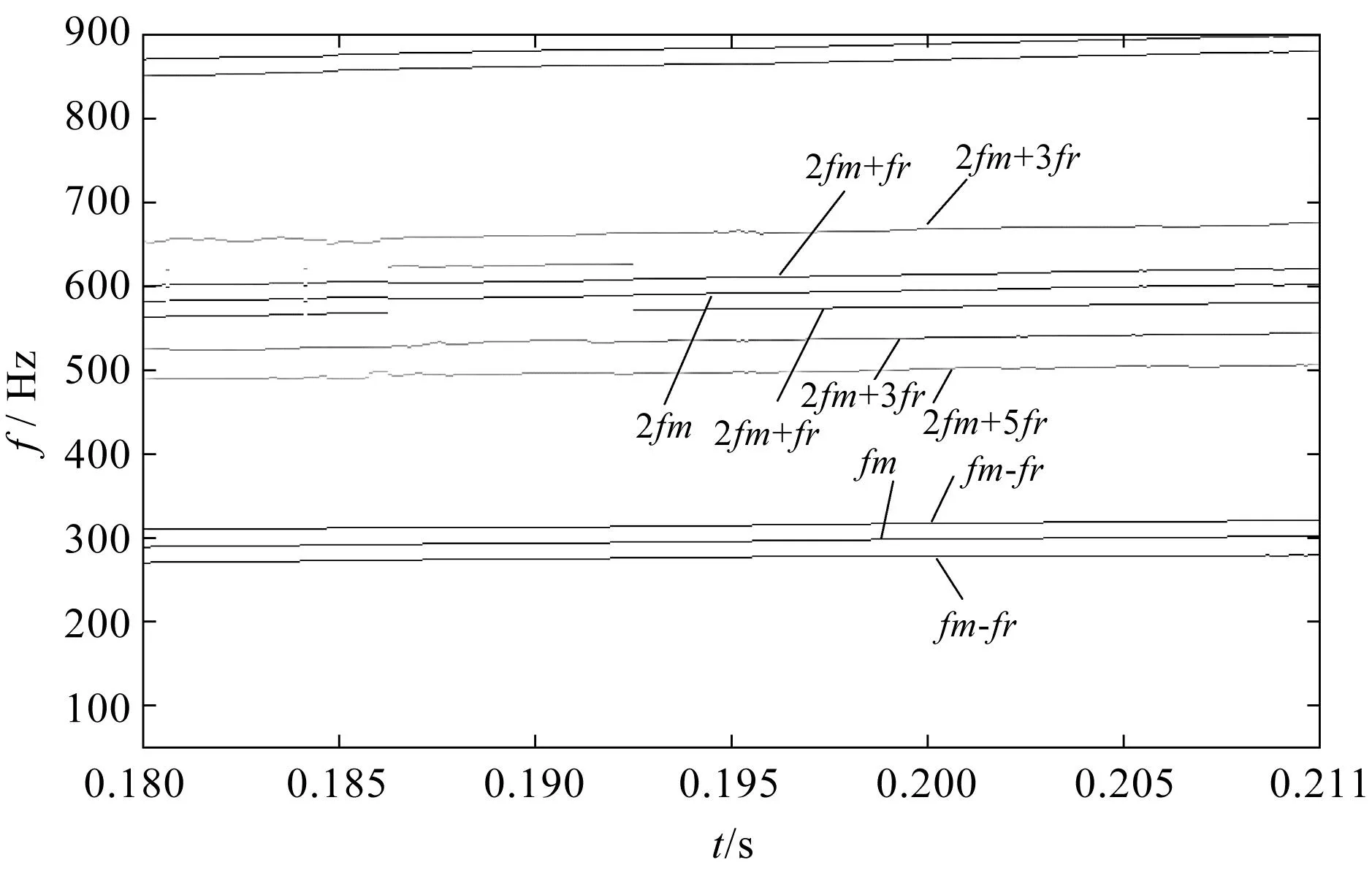
图13 PFSRLCT得到的时频表示Fig.13 TF representation obtained by FPRSLCT
观察图13可知:PFSRLCT所得的时频结果可以检测到啮合频率的啮合频率fm、二次谐波2fm及其间隔为小齿轮转频fr的边频带。
由上述的齿轮故障振动信号特征表明,小齿轮轮齿存在故障,这与试验所设置的故障一致。
对于其他参考方法的窗口长度,笔者均设置为0.1 s,VLSCT的Nwl设置为30,获得的时频表示如图14所示。
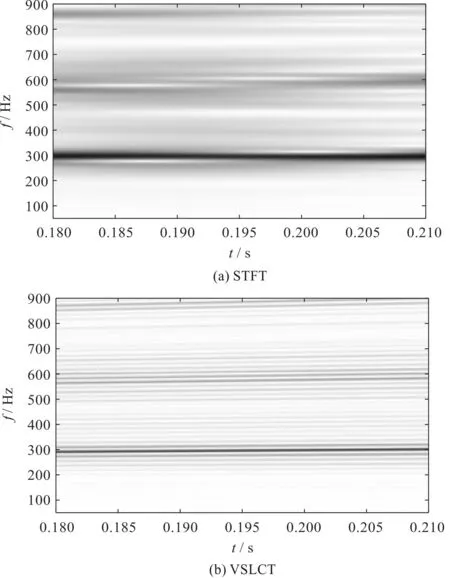
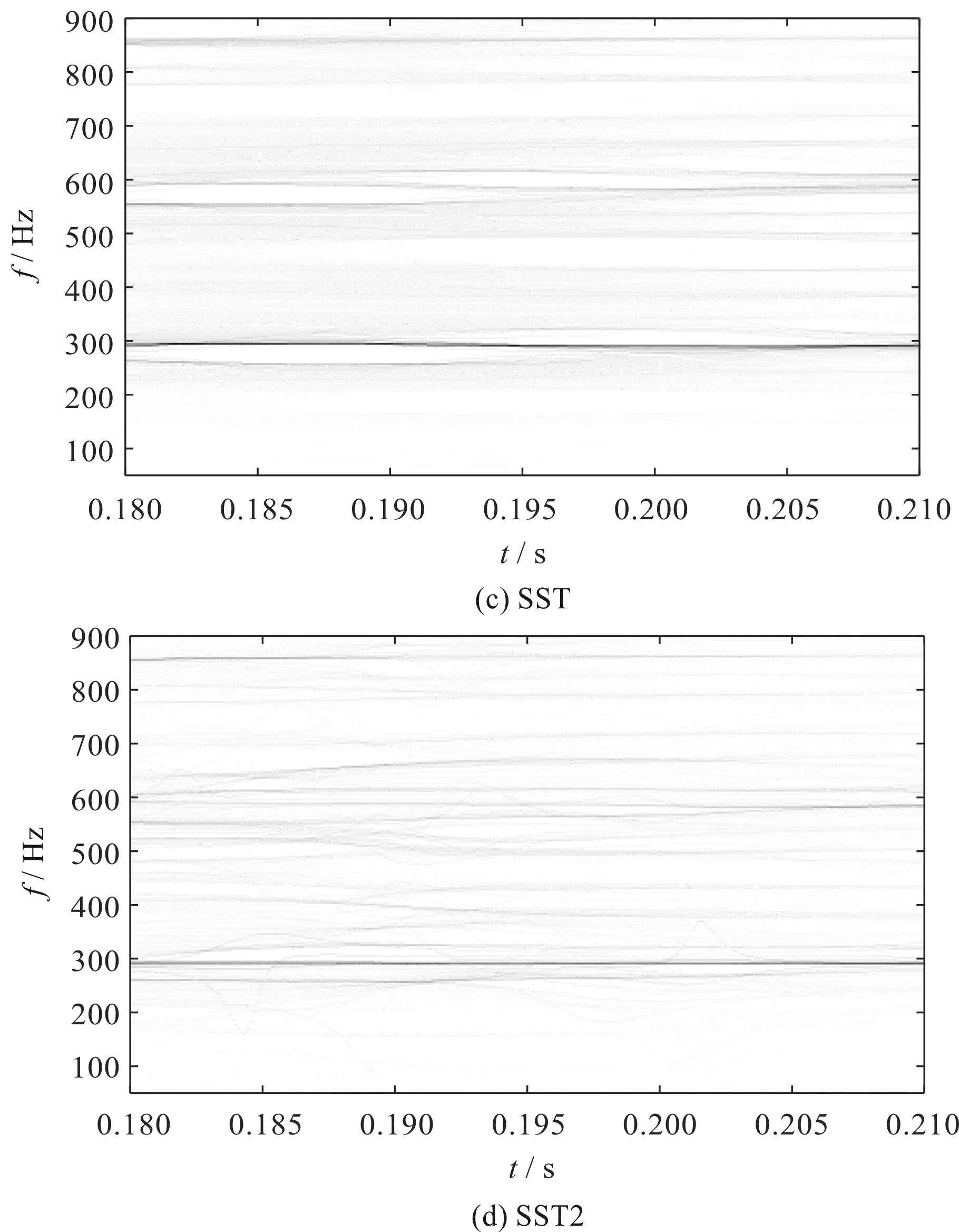
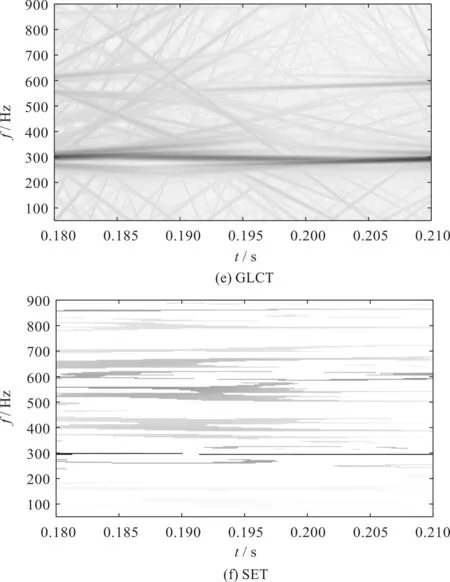
图14 试验信号的时频变换Fig.14 TF representation obtained by other methods
由图14可以看出:这几种方法均能揭示强成分,如啮合频率的啮合频率fm;但是STFT、GLCT、SET、SST和SST2无法检测到弱成分,如啮合频率谐波的边频带fm±fr;VSLCT可以检测到弱成分,但是所得到的时频表示的时频聚集度较低。
为了衡量采用各种方法所得到得时频结果的能量集中度,笔者通过计算获得各种方法的Rényi熵,如表3所示。
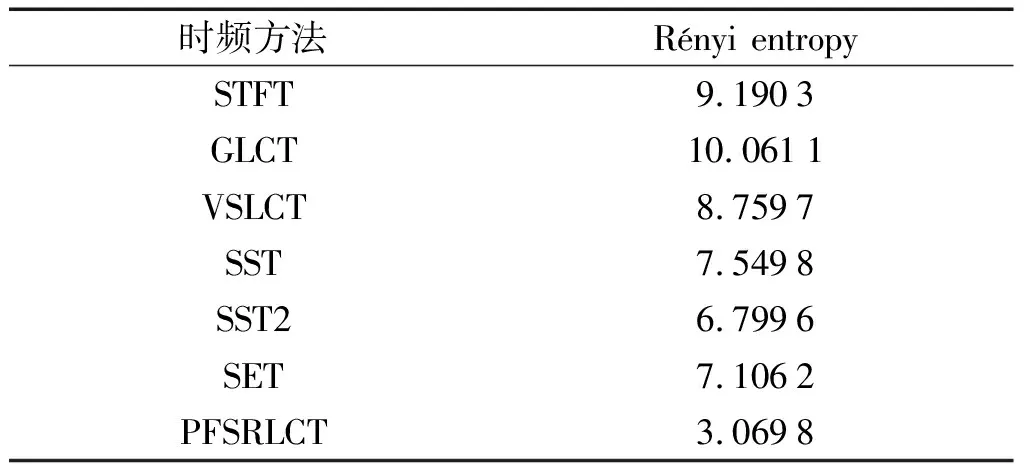
表3 各种方法的Rényi熵
由表3可知:PFSRLCT所获得的Rényi熵最小,为3.069 8,并且明显低于其他时频方法。
由此可以证明,PFSRLCT所获得时频能量集中度最高,相对于其他时频方法有明显优势。
6 结束语
根据齿轮故障信号特征,笔者提出了一种用于齿轮故障诊断的时频分析方法——PFSRLCT。
该方法重新定义了Chirplet变换中的变换核,以峭度为标准,自适应选择各个时间窗内Chirprate。修改后的方法可以用于分析具有成比例的瞬时频率轨迹的多分量非线性信号。该方法进一步利用提取的时频脊线与狄拉克函数构成重分配算子,对时频结果进行了重分配,进一步增强了时频域结果的聚集度。
笔者将PFSRLCT方法分别应用于模拟信号和齿轮故障信号中,并将其与其他方法进行了对比。
研究结论如下:
1)模拟信号分析结果表明,在信噪比为-2 dB~10 dB时,所得的频率估计误差均小于0.01;在信噪比为-1 dB时,所得Rényi熵仅为4.745 1,PFSRLCT的噪声鲁棒性相较于其他方法更强,能量集中度更高;
2)PFSRLCT用于齿轮故障信号,其可以清淅地分辨出啮合频率及其边频带,依据齿轮故障信号特征,可判别出齿轮故障,验证了PFSRLCT在齿轮故障诊断中的有效性;
3)PFSRLCT用于齿轮故障信号可以获得高质量的时频表示,相较于其他方法,其可以清晰地揭示出弱分量成分,同时所获得时时频结果的Rényi仅为3.069 8,明显低于其他方法,其具有高时频能量集中度和显著的优越性。
PFSRLCT方法在齿轮故障诊断中取得了良好效果,但是在处理数据量较大的信号时,对计算机性能要求高。后续,笔者将对该方法的算法进行优化改进,以降低计算的复杂度。

