基于时频图与双通道卷积神经网络的轴承故障识别模型*

张政君,井陆阳,徐卫晓,战卫侠,王晓昆

(青岛理工大学 机械与汽车工程学院,山东 青岛 266000)

0 引 言

目前,轴承已经被广泛应用于各个领域的机械设备中,其健康状况对机械设备的寿命、稳定性都有非常大的影响[1]。因此,对轴承进行故障诊断具有重要意义[2]。

轴承故障诊断最常见的方法是对轴承振动信号进行监测[3],利用传感器对轴承的振动信号进行采集,并利用时频分析方法获取其信号特征。常见的时频分析方法包括时序分析[4]、谱峰度[5]、稀疏表示[6]、Wigner Ville分布(Wigner Ville distribution, WVD)[7]和连续小波变换[8]等。采用平滑伪Wigner Ville分布(SPWVD)对WVD与平滑函数进行卷积,可有效降低WVD中交叉项的影响[9]。经验模态分解(empirical mode decomposition, EMD)[10]和集成经验模态分解(ensemble empirical mode decomposition, EEMD)都可以自适应地将非线性非平稳信号转换为多个频段的本征模态函数。

但以上两种方法容易受到模态混叠和端点效应的影响。为了解决这些问题,学者们又提出了变分模态分解(VMD)。

VMD为分解问题提供了一个具有严谨数学基础的解决方案,并且VMD对噪声具有很强的鲁棒性[11],可以有效地避免模态混叠现象,其在环境科学[12]、生物医学信号[13]等领域都展现出了良好的效果。但惩罚因子α和分解层数K的选择对VMD效果有很大的影响,其往往依赖人工判断。

以样本熵峭度指标最小值为目标函数,采用灰狼优化对VMD进行参数寻优,并对VMD处理后得到的分量进行SPWVD运算,可以得到高分辨率的时频图,并用于特征的提取。

随着人工智能技术的飞速进步,深度学习方法逐渐被应用在了故障诊断领域。卷积神经网络(CNN)作为深度学习的重要分支,其布局接近实际的生物神经网络,图像可以直接输入网络,这一特点避免了特征提取和分类过程中数据重建的复杂度。

陈宇航等人[14]使用快速傅里叶变换及CNN,对轴承故障进行了识别,取得了较高的准确率。许同乐等人[15]利用EEMD对信号进行了降噪等预处理,将处理后的信号输入到改进后的CNN中,解决了微弱故障特征提取困难的问题。肖俊青等人[16]利用完全自适应噪声集合经验模态分解模糊熵以及CNN,进行了不同工况下轴承的故障诊断,解决了轴承故障信息难以提取的问题。

以上结果表明:时频分析结合CNN提取特征的方法在故障诊断方面有着优良的效果。

但以上研究忽略了CNN更适合对图像进行特征识别的特点(因为其局部权值共享的特殊结构),并且其训练过程需要大量数据,以保证CNN的性能。

鉴于以上情况,笔者从轴承振动信号的时频图出发,提出一种基于时频图和双通道CNN的轴承故障诊断方法。

笔者使用SPWVD处理参数优化后的VMD得到的模量分类,以及直接对轴承信号进行CWT运算这两种方式得到时频图,并以此作为数据增强手段;将两种方式得到的时频图分别作为双通道CNN中一个通道的输入,在神经网络中提取时频图的深层次特征,以期完成对轴承进行故障诊断的任务。

1 时频分析方法

1.1 变分模态分解

变分模态分解(VMD)是一种自适应信号分解算法。它可以将信号分解为多个分量,其实质和核心思想是变分问题的构造和求解。

其算法流程如下:

首先,建立变分模型,即:

(1)

(2)

式中:∂t为偏导数运算;δ(t)为狄利克雷函数分布函数;*为卷积;f为原始信号;K为IMFs的个数。

其中:{uk}={u1,u2,…,uk}为VMD分解得到的K个模态分量IMFs;{ωk}={ω1,ω2,…,ωk}为各IMF的中心频率。

然后,使用惩罚因子和乘法算子将问题转化为无约束问题,增广拉格朗日函数为:

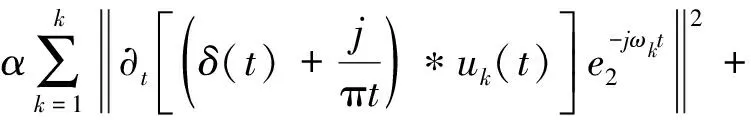
(3)

式中:λ为拉格朗日常数;α为惩罚因子。

最后,为了求解变分问题的最优解,必须采用交替方向乘子法(alternating direction method of multipliers,ADMM)对变量进行更新。

(4)

(5)

(6)

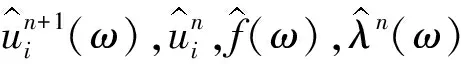
VMD算法的主要迭代求解过程如下:

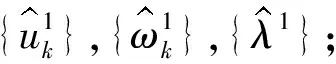
2)n=n+1,进入循环,其中n为迭代次数;

3)更新uk,ωk,λ;

4)重复式(4)～式(9),直到满足迭代停止条件,即:

(7)

式中:ε为预先设定的收敛阈值。

VMD的效果受参数K和α的影响,因此需要使用灰狼优化算法(GWO)对参数进行迭代寻优。

GWO是一种基于种群的元启发式算法,是从灰狼(Canis)的种群结构、社会等级和狩猎机制中得到启发而创立。与其他元启发式优化算法相似,GWO在机器学习模型超参数和机器学习特征选择优化领域具有良好的效果。GWO的实现方式简单,用于迭代的参数数量少,可以满足迭代过程中目标函数最小值或最大值寻优的要求,并且有收敛速度快、求解精度高等特点[17]。

对于优化算法的目标函数,样本熵(sample entropy, SampEn)是一种判断时间序列复杂程度的算法,其对时间序列长度的依赖性少、抗噪能力强,有利于对故障特征进行提取[18]。

峭度(kurtosis,KU)作为一个无量纲参数,对振动信号中由早期故障引起的冲击信号非常敏感,当振动信号中冲击成分以及故障信息越多时,其峭度值越大。

因此,笔者结合两者的优点,构建目标函数样本熵峭度指标(kurtosis sample entropy,KUSE):

(8)

式中:KU为所有模态分量峭度最大值。

在其优化过程中,目标函数达到最小值时可获得最优的参数组合。

1.2 平滑伪Wigner Ville分布

Wigner Ville分布(WVD)作为Cohen类双线性时频分布中最基本一种分布,其实质是将信号的能量分布于时频平面内。它的优点是不加窗、分辨率高。然而将其应用于多个信号分量时,会受到交叉干扰项的影响。因此,如何减小交叉项就成了WVD性能改进的主要目标。

平滑伪Wigner Ville分布(SPWVD)的实质就是在时域和频域分别对信号进行加窗处理,达到平滑滤波的作用,有效抑制干扰项带来的干扰[19]。其定义为:

(9)

式中:g(u),h(τ)为两个偶窗函数。

此处,笔者将不同损伤类型的轴承信号分别输入到经过灰狼优化的变分模态分解(GWO-VMD)中,以获得K个模态分量;再对分解出来的分量进行SPWVD计算,对结果进行同一坐标系下的累加,以降低信号的不稳定性;最后进一步降低交叉项的干扰,以得到对应的高分辨率二维时频图。

1.3 连续小波变换

小波变换的初衷就是体现信号时域信息,故而小波变换相比傅里叶变换(FT)增加了一个变量,以展现时域的信息[20-21]。

小波函数的一般形式如下:

(10)

对于任何一个随机信号的函数,相应的连续小波变换(CWT)表达式为:

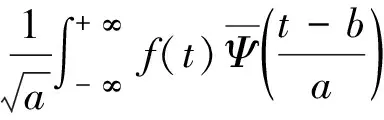
(11)

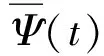
连续小波变换(CWT)可以将原始信号从时域变换到时频域,其结果是原始振动信号在时频域的归一化表示。CWT将每个信号段转换为标量图图像,表示其系数的绝对值。

此处笔者把Morlet小波作为小波函数的CWT,将其应用于轴承信号的时频分析中。

2 卷积神经网络

2.1 二维卷积神经网络

卷积神经网络是一种多级神经网络。其基本结构由输入层、卷积层、池化层、全连接层及输出层构成。CNN经常被用于处理输入为一维数据的自然语言处理和语音识别任务。CNN的主要特点有两个方面(权重共享和空间池化),这使得它非常适合处理输入为二维图像数据的计算机视觉应用。

对于每个特征映射,首先由具有局部接收域的卷积核对输入进行卷积操作;然后,在卷积结果中加入一个偏置项;最后,应用激活函数。

其数学表达式定义为:

(12)

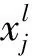
为了减少CNN中参数的数量,同一特征图的卷积核共享相同的权向量和偏置。通常需在每个卷积层上加一个最大池化层(max-pooling),利用子采样操作生成低分辨率的特征图。

Max-pooling定义如下:

(13)

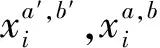
池化层减小了输入特征映射的大小,同时保持了特征映射的数量。笔者采用子采样技术,使CNN中的参数数量进一步减少。最后一个池化层后面是一个全连接层。全连接层中的每个神经元都连接到最后一个池化层中的所有特征映射。

笔者提取全连接层的高级特征,作为输出层的输入;然后生成CNN模型的预测输出;最后使用最小化损失函数对网络的参数{W,b}(权重向量和偏差)进行微调,计算预测输出y与目标输出t之间的误差如下:

(14)

式中:{W,b}*为优化后的参数;n为被标记样本的数量;j为损失函数。

此外,笔者采用反向传播算法对网络进行基于梯度的监督训练。

2.2 CNN结构的设计

AlexNet模型作为经典CNN模型之一,其优点包括:

1)可以对数百万张ImageNet图像进行训练,使用ReLU作为激活函数,解决了网络结构较深时sigmoid的梯度发散问题;

2)Dropout在训练过程中随机忽略部分神经元,减少了神经元之间复杂的相互适应关系;

3)在CNN模型中使用重叠最大池化层,提高了特征的丰富度,同时避免了平均池化层的模糊效应;

4)建立了局部神经元活动的竞争机制,以提高模型的泛化能力。其网络结构包括5个卷积层和3个全连接层。

笔者所使用的双通道CNN模型在AleXNet的结构上进行了改进。

双通道卷积神经网络结构示意图如图1所示。

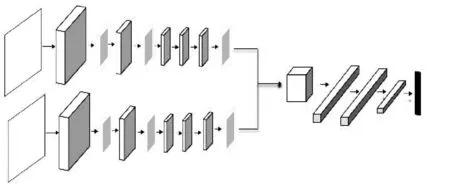
图1 双通道卷积神经网络结构示意图Fig.1 Schematic diagram of dual channel convolutional neural network

双通道神经网络模型参数如表1所示。

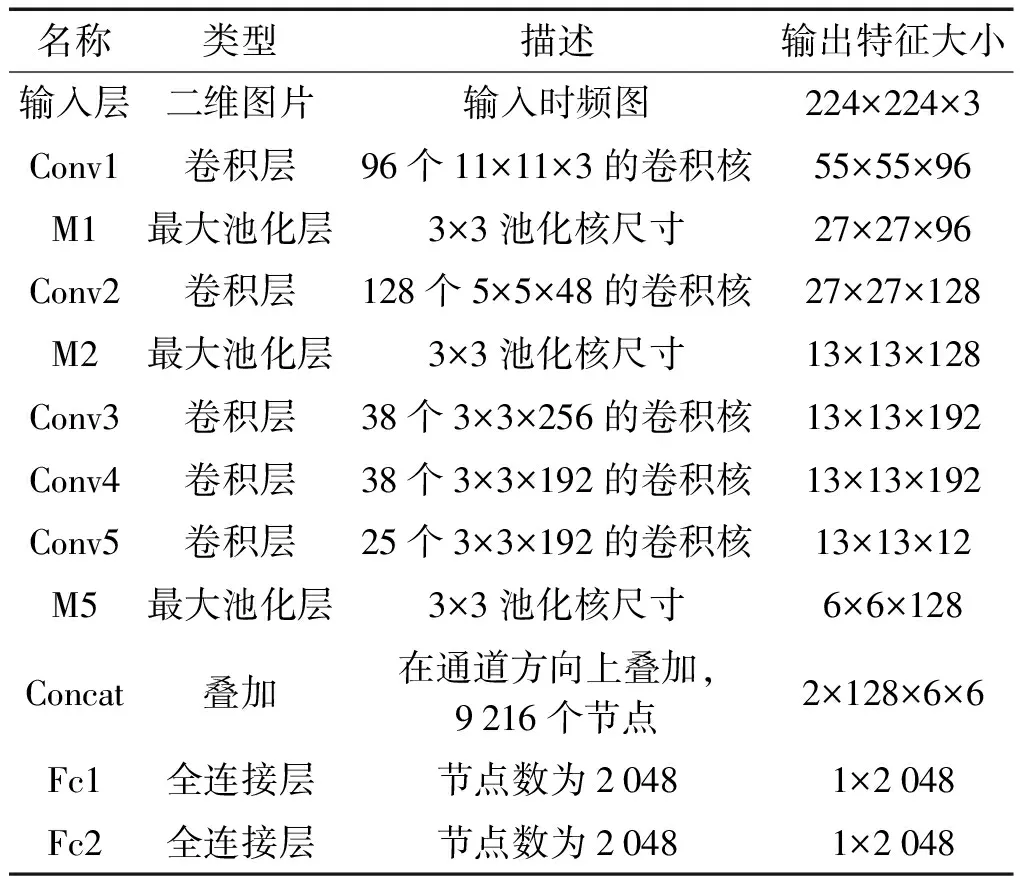
表1 双通道神经网络模型参数

表1是对图1结构的具体描述。

表1中,网络结构第一层表示输入层,两个并行的通道的结构和参数一致;Conv表示卷积层,选择ReLU作为激活函数;M表示最大池化层;Concat代表将两个通道输出的特征图进行叠加;Fc代表全连接层,并在全连接层使用dropout防止网络出现过拟合。

每个通道包括5个卷积层,3个池化层,时频图的特征被提取出来;然后在汇聚层进行叠加和特征融合,经过两个全连接层将二维图像特征转化成一维的向量;最后使用SoftMax分类器对故障进行分类。

3 基于时频图和双通道CNN的诊断模型

笔者所提出的基于时频图和双通道CNN的轴承故障诊断方法(模型)流程如下:

首先以前文提到的KUSE最小值作为适应度函数,使用灰狼优化算法对VMD进行参数优化,利用VMD对轴承原始信号进行处理,得到K个模态分量,对模态分量进行SPWVD计算,并对结果进行累加,得到GWOVMD-SPWVD时频图;再对振动信号进行小波变换,以得到时频图,将这两种时频图输入到双通道CNN中,提取不同故障类型和损伤程度时频图的特征;最后由SoftMax完成故障分类的任务。

基本流程图如图2所示。

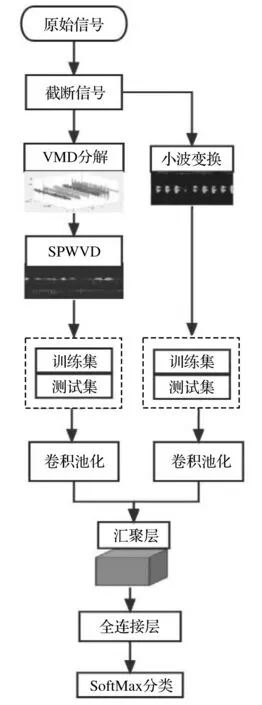
图2 方法流程图Fig.2 Method flow chart

4 实验及结果分析

4.1 实验数据

此处的实验数据来自某旋转机械故障模拟试验台。

该试验台主要由驱动电机、转速转矩传感器、加速度传感器、负载和测试轴承等部件组成。其构造实物图如图3所示。

图3 轴承故障试验台Fig.3 Bearing failure test stand

其中,实验轴承为圆柱滚子轴承,型号为NU205M,滚动体个数为13。

笔者使用加速传感器采集XYZ这3个方向的振动信号,其中Y为径向(垂直方向),Z为轴向(水平方向),X为切线方向(水平方向)。

实验用圆柱滚子轴承包括4种状态,分别为正常和内圈故障、外圈故障和滚动体故障。每个故障状态包括轻微损伤和严重损伤两种损伤程度,共计7种故障类别。轴承故障为人为故障,即在轴承不同部位,采用砂轮机磨削的方法加工出与轴线平行的缝隙。

实验数据来自传感器,即采用加速度传感器采集其Y方向的振动信号。数据采集时,采样频率为100 kHz,采样时间为10 s,实验中电机转速为900 r/min。在采集到的振动数据中,以2 048个点截取为一个样本(每种类别样本数均为100)。

试验台数据集的分类情况如表2所示。

表2 试验台数据集分类情况

4.2 时频图生成

笔者使用GWOVMD-SPWVD和CWT方法对轴承数据进行处理。其中,CWT使用cmor3-3作为小波函数对信号进行运算;对于GWOVMD-SPWVD方法,使用样本熵峭度指标最小值作为适应度函数,使用GWO对VMD进行参数优化,迭代次数设置为80。

适应度变化曲线如图4所示。

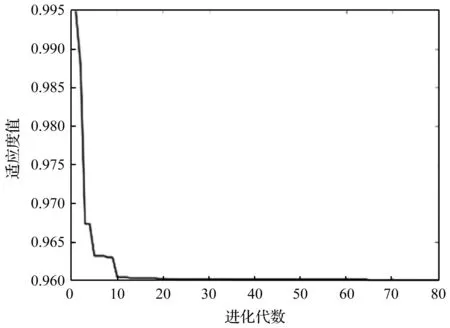
图4 适应度变化曲线Fig.4 Fitness curve

由图4可以看出:随着迭代次数的增加,适应度函数逐渐收敛,最终得到最优VMD参数组合。

笔者对每种故障类型分别进行VMD参数优化,得到了故障类型及对应的VMD参数,如表3所示。

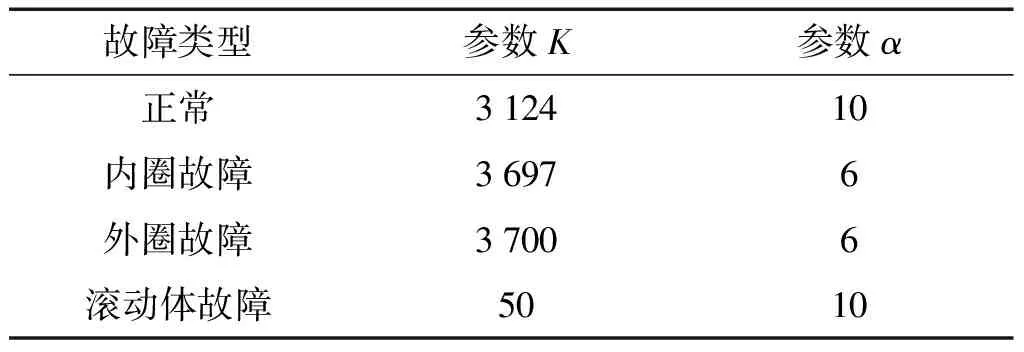
表3 不同故障类型对应的VMD参数

笔者先对不同故障状态的样本进行VMD处理,得到相应的模态分量;再对分量进行SPWVD运算,得到相应的时频图;最后对不同工况的二维时频图进行特征提取,以进行最后的轴承故障识别。

由于篇幅所限,此处笔者仅展示使用GWOVMD-SPWVD方式得到的时频图。

不同故障类型及损伤程度所对应的时频图,如图5所示。

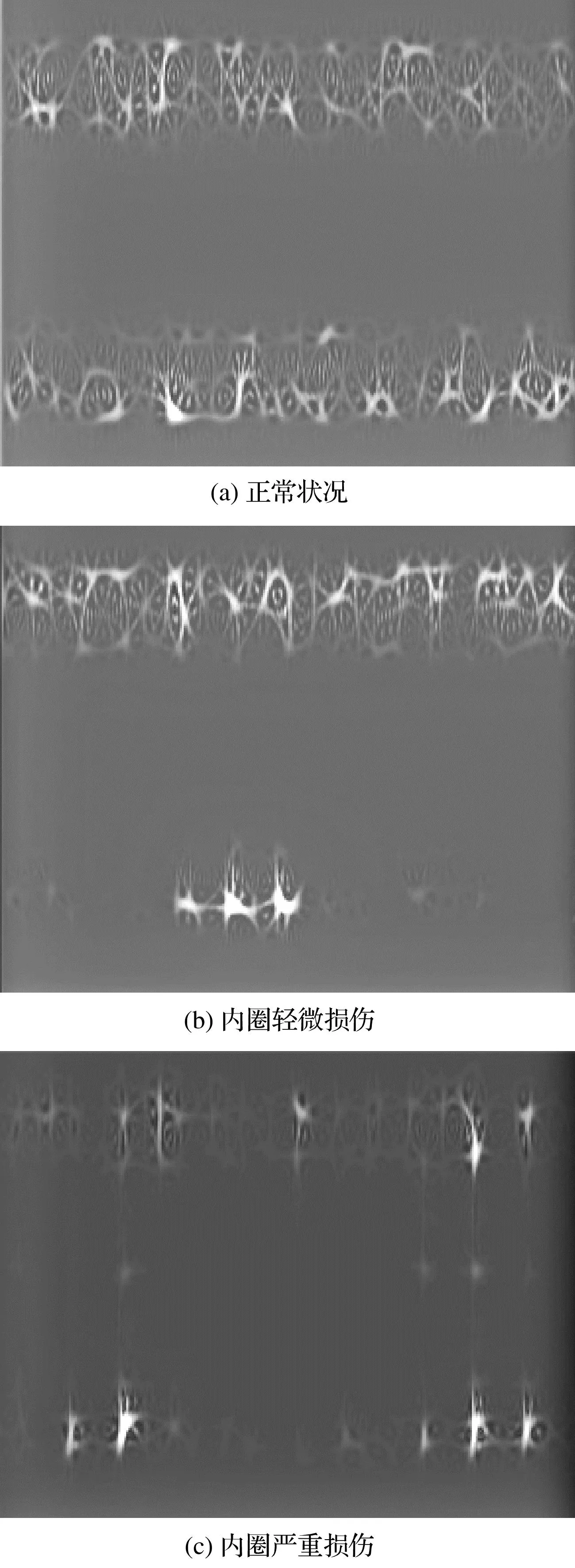
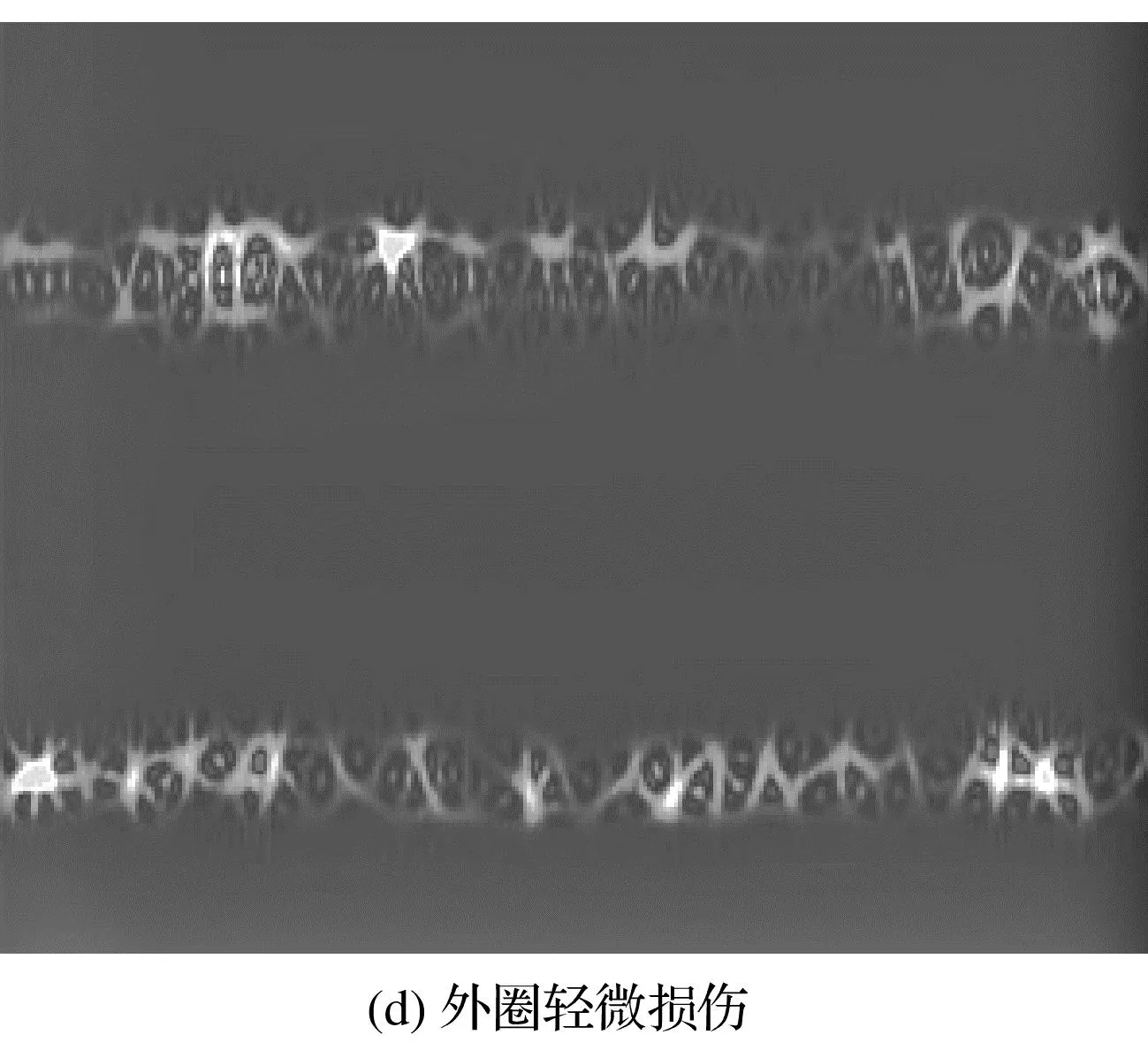
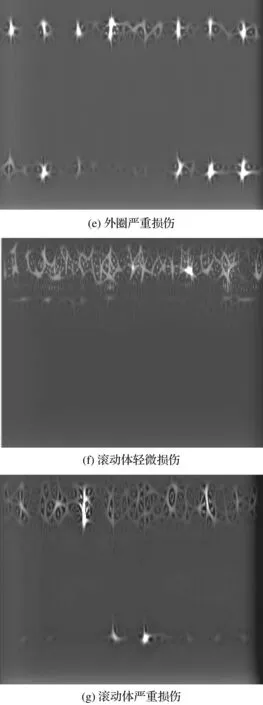
图5 不同损伤情况时频图Fig.5 Time-frequency diagram of different damage conditions

由图5(a)可知,在正常工况下,轴承时频图像的能量较为均匀地分布在低频段和高频段;在5图(a)～5图(g)中,工况图像的能量分布相对集中在某个频段,且存在明显的差别;使用该处理方式可以清晰地判断出轴承的健康状况。

4.3 试验过程与结果分析

在图像输入神经网络前,笔者随机选取不同工况下图像数据集的25%作为测试集,其余为训练集。在试验台数据集中,采用两种时频图生成方式分别得到700张图像,共计1 400张时频图(其中1 050张作为训练,350张作为测试)。

笔者将图像输入至双通道神经网络中,选择训练参数如下:选择Adam优化器,设定学习率为0.000 1,设置Batchsize为32、MaxEpochs为150。

模型训练过程精确率和损失值如图6所示。

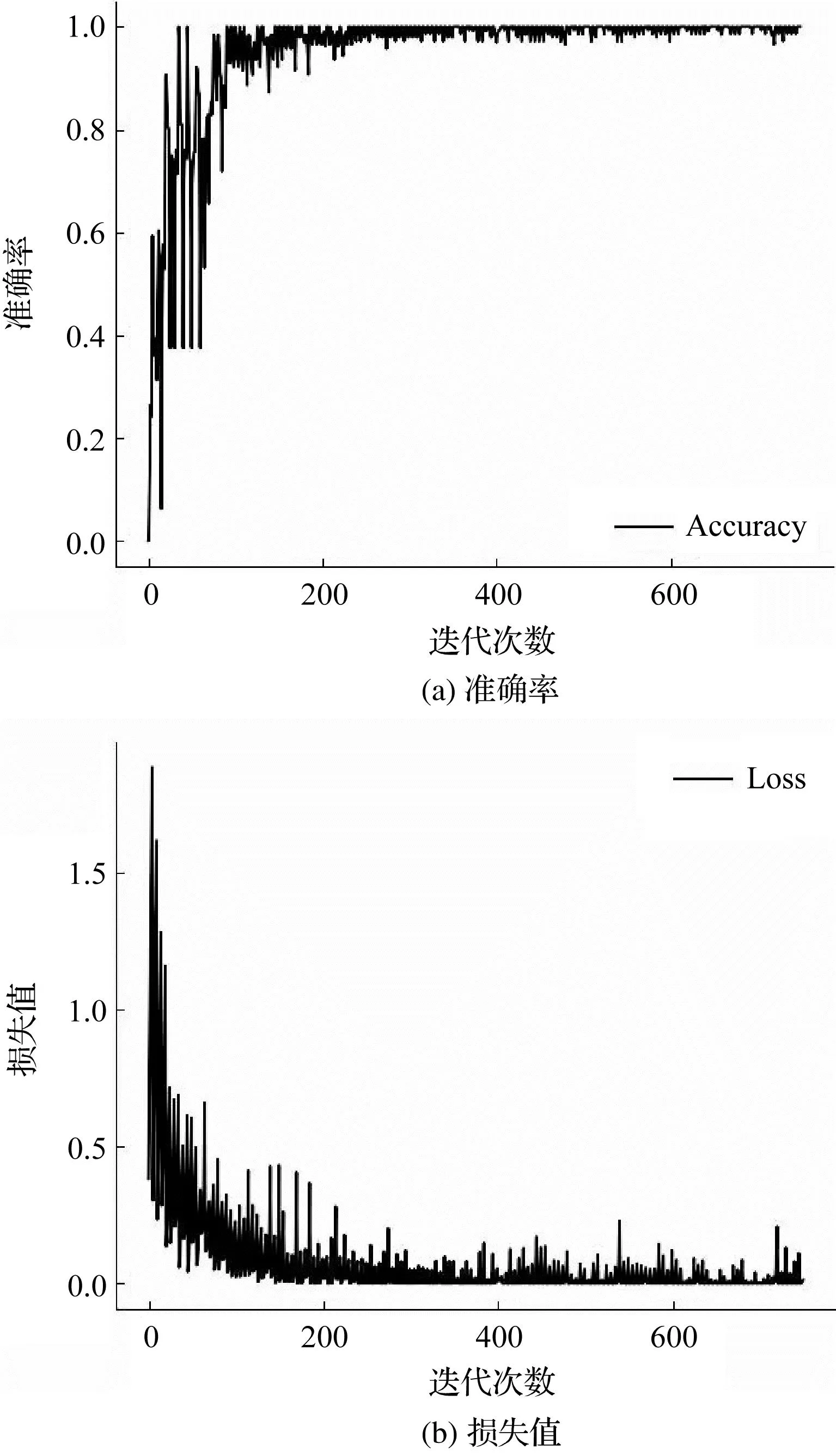
图6 模型训练过程精确率和损失值Fig.6 Training process accuracy rate and loss value

图6展示了模型训练过程中损失值和模型准确率的变化过程,其中,随着迭代次数的增加,网络的损失值不断下降,准确率也逐渐上升;在前200次迭代中,损失值下降和准确率提高的速度较快;在迭代中期,图像出现细微的波动,并逐渐趋于平稳;最后达到一个稳定状态。

经过多次迭代,得到最终的准确率和损失值分别为99.69%和0.000 4。

以上结果表明:基于时频图和双通道CNN的诊断模型对具有较强的轴承故障识别能力和鲁棒性。

4.4 模型性能对比

为进一步验证基于时频图和双通道CNN的轴承故障诊断模型所具备的优越性,笔者使用的数据集均为试验台采集到的数据,将上述双通道模型与CWT-CNN模型、GWOVMD-CNN模型和基于机器学习的傅里叶变换-支持向量机(FT-SVM)模型进行处理结果对比验证。

为了降低实验结果的偶然性,验证模型的稳定性,笔者对每个模型进行10次实验,并统计每次试验的结果,计算模型的平均准确率和准确率的标准差,以说明模型准确率的波动情况。

最后得到的各个模型性能(即平均准确率和标准差),如表4所示。

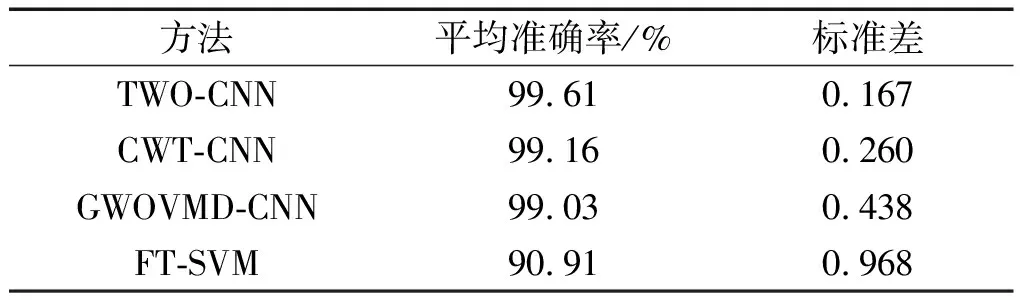
表4 模型性能

其中,训练准确率变化曲线如图7所示。

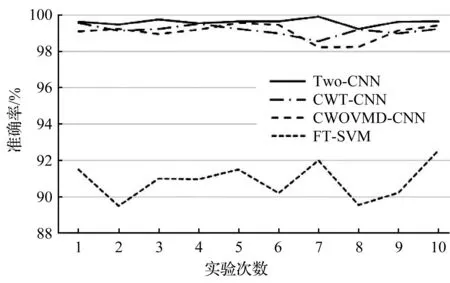
图7 训练准确率变化曲线Fig.7 Training accuracy curve

图7中:TWO-CNN表示笔者提出的双通道CNN模型;CWT-CNN和GWOVMD-CNN模型是笔者提出的双通道模型中的一个通道;FT-SVM表示FT-SVM模型。

笔者将轴承信号(包括包络熵值、峭度等在内的9种时频域特征参数),经过归一化和降维处理后,输入到SVM分类器中进行故障分类。

基于时频图和双通道CNN的模型平均准确率为99.61%,准确率标准差为0.167,相比单通道模型和机器学习模型,该模型有着更高的准确率和更出色的稳定性。

由此可以证明,基于时频图和双通道CNN模型在轴承故障诊断方面具有一定的优越性。

5 结束语

由于采用传统信号处理方法难以从轴承振动信号中提取可以准确反映轴承运行状态的特征,为此,笔者提出了一种基于时频图和双通道CNN的轴承故障诊断方法。

首先,笔者使用GWOVMD-SPWVD和CWT两种方式处理振动信号,并得到了其时频图;然后,将时频图作为双通道CNN的输入,采用双通道CNN故障诊断方法对轴承进行了故障诊断。最后,将该方法与单通道CNN和SVM方法进行了对比,利用轴承故障试验台数据对其有效性进行了验证。

研究结果表明:

1)采用GWOVMD-SPWVD和CWT两种方式可以获得高分辨率特征信息丰富的二维图像,而且可以作为一种数据增强的方式扩充数据集;

2)使用的双通道CNN在轴承故障实验中的准确率达到了99.69%,在10次实验中的平均准确率为99.61%。相比其他两种单通道,CNN模型的平均准确率分别提高了0.45%和0.58%。可见双通道CNN结构对轴承故障有更好的诊断效果;

3)根据实验结果可知,双通道CNN的平均准确率相比SVM提高了8.7%,这表明双通道CNN相比SVM可以更有效地提取图像深层次特征,并在较深层完成特征融合和轴承故障分类的任务。

鉴于神经网络层数的大小、参数的选择等因素对模型准确率有着很大影响,因此在后续工作中,笔者将对神经网络的具体结构及其参数优化做进一步的研究。