有限纠偏能力的多差速单元循迹协同控制

丁聪，赵蕾磊

(1.中船重工鹏力(南京)智能装备系统有限公司，江苏南京 210000；2.中国航天科工南京晨光集团江苏金陵智造研究院，江苏南京 210000)

0 前言

航空航天等重工业中，多见舱段、机翼等具有大体积、大质量特性的部件。若使用重载AGV搬运该类超大超重产品，不仅可以提高转运效率，还可以避免现有吊装转运方式存在的掉落风险，因此将重载AGV应用于重载场合逐渐引起加工制造业及学者的关注[1-3]。

为使AGV具备更高的承载能力和驱动能力，重载AGV需使用多套轮系驱动。由于差速轮的双轮结构使得单套轮系具有更强的驱动力和承载力，与直接转向舵轮相比，相同承载需求下使用轮系数量更少、占用空间更小，因此差速轮更适合重载场合。当前差速驱动相关研究多集中在汽车底盘差速系统[4-8]、多差速驱动单元协同控制[9-17]或含有差速承载单元的轮系控制[18-19]。汽车底盘差速系统与AGV原理不同，不在此次讨论范围；使用单套舵轮驱动、差速轮承载的AGV由于其结构限制，车体旋转中心只能位于差速轮轴线上，AGV不具备全向移动能力，灵活性及循迹能力较差，也不作为此次研究的对象。而针对双轮均具备驱动能力的多差速驱动单元控制的研究，多集中有限(一组或两组轮系最为常见)差速轮系且差速驱动单元轮系旋转中心均位于车体中轴线的应用情景。如文献[17]提出一种使用3套差速驱动单元协同控制方法。该研究基于多机器人编队控制方法，将前轮作为领航单元，利用两轮间距离差作为刚性约束条件控制AGV进行路径跟踪。但是，该方法基于“3套差速驱动系统中心均位于车体中轴线”提出了约束并基于该约束提出了跟随单元速度控制律，轮系布局受限，不具备扩展性。AGV在实际使用时常与循迹、跟踪等功能密不可分[20-24]。文献[25]虽然基于常见重载AGV轮系排布介绍了差速轮系直线行进、斜行、原地转弯等几种典型运动形式下各轮速度分配，但仅限于简单的纯运动学分析，未考虑循迹、跟踪等实际复杂应用情景，实用性不高。

直接转向舵轮具有转向电机和驱动电机，可实现AGV全向移动，循迹精度高；差速轮的左、右轮各有一套驱动电机，依靠驱动速度差转向，因此不仅需满足同一AGV内的刚体运动学关系，各轮系内部也存在耦合，循迹运行也更加困难。为使得多差速轮驱动的AGV拥有与直接转向舵轮驱动相似的良好循迹能力，同时在充分考虑纠偏需求时兼顾差速轮运动学特性、整车刚体运动学特性及良好的可扩展性，提出了多差速单元循迹协同控制方法。

1 差速轮运动特性

如图 1所示，一套差速轮为双轮结构，两轮均为驱动轮，分别配有驱动电机。差速轮不具备直接转向能力，需通过两轮速度差转向。如图 2所示，记一个差速驱动模块中心速度vc，两轮中心距离的一半为dw，左轮速度为vl，右轮速度为vr；轮系绕点O旋转，转动角速度为ω，旋转半径为R。一个运动周期后，轮系绕点O转过角度Δθ1，轮系中心速度方向有变化量Δθ2。左、右两轮速度可表示为

vl=|ω|·(R+dw)

(1)

vr=|ω|·(R-dw)

(2)

联立以上两式可得：

(3)

由于Δθ1=Δθ2，因此轮系转动角速度ωd与ω相等。当轮系逆时针旋转时，vr>vl，ω为正值；当轮系顺时针旋转时，ω为负值。由几何关系易得轮系中心速度vc为

(4)

由式(1)—(4)，当已知轮系中心速度vc及转动角速度ω时，可得左右轮速度为

vl=vc-ω·dw

(5)

vr=vc+ω·dw

(6)

ω受驱动轮驱动能力上限限制，设驱动电机可驱动轮系最大运动速度为vmax，当vc=0时，轮系有最大旋转速度ωmax，此时ωmax=vmax/dw。

图 2 差速轮速度分配

差速轮转向后中心位置及中心速度指向发生变化。当两个运动周期间隔t较小时，可简化为图 3所示状态：车轮中心沿图中vc方向移动距离Δd，且有Δd=vc·t；在新的中心位置，vc指向发生变化，与上一时刻中心速度方向相比旋转了角度Δθ，且有Δθ=ω·t。

图 3 小周期内差速轮姿态变化示意

2 多差速驱动单元协同控制

2.1 基于偏差状态的控制

此次研究针对的AGV简化模型如图4所示，采用4套差速轮驱动的形式。矩形线框表示连接各轮系旋转中心的车架体。建立车体坐标系x-y，其中x轴正向指向车体前进方向。四轮分别编号1—4，各轮旋转中心位置在车体坐标系中可表示为式(7)所示矩阵形式。若使用更多轮系，可将该矩阵按需扩展。

(7)

如图5所示，建立世界坐标系X-Y，AGV循迹线设为Y轴。车体坐标系原点在世界坐标系中表示为(xcyc)，车体坐标系x轴相对于X轴有姿态角θc。理想情况下，车体中心应位于Y轴且x轴与Y轴重合，但位姿偏差不可能被完全消除，图中所示车体中心相对轨迹线有距离偏差dc，记dc=|xc|；定义x轴与轨迹线的夹角较小值为角度偏差δc。使用vc表示中心速度，使用ω表示车体旋转角速度，为消除位姿偏差，设计跟踪控制律：

(8)

式中：k1为线速度系数，k1>0；k2为角速度系数，k2>0。

vc与车体x轴有夹角β，指向轨迹线。在上述线速度及角速度组合下，AGV将靠近轨迹线，同时车体姿态得到调整。

设0时刻车体中心位于轨迹线左侧且有角度偏差δc，如图6所示。按式(8)所示控制律，需为其中心规划指向轨迹线方向的速度及可使车体逆时针旋转的角速度，即在到达1时刻时，在坐标系x1-y1下，各轮有图7所示摆角θi(1)及轮系中心速度vi(1)使得车体中心速度vc(1)与x1轴有夹角β(1)，车体旋转半径大小为r(1)。

图 6 0时刻车体状态示意

设车体参考速度大小为vd。在车体坐标系x0-y0下，取各轮中心速度vi(0)=[vd0 0]T。期望到达1时刻时，中心速度为

vc(1)=

[|vc(1)|cosβ(1) |vc(1)|sinβ(1) 0]T

(9)

并有角速度为ω(1)。记：

ω(1)=[0 0ω(1)]T

(10)

各轮速度向量可表示为

vwheel(1)=[vc(1)1×4]+[ω(1)1×4]×P=

(11)

各轮系摆角为

(12)

设ωi(0)为各轮旋转角速度，计算方法为

(13)

viL(0)=|vi(0)|-ωi(0)·dw

(14)

viR(0)=|vi(0)|+ωi(0)·dw

(15)

将上述计算结果赋予轮系，AGV可从x0-y0状态运动至x1-y1状态，如图7所示。各轮摆角变化至θi(1)，车体姿态未发生变化。

在下一运动周期，期望车体从1时刻状态到达2时刻状态，即在坐标系x2-y2下，各轮有图8所示摆角θi(2)及轮系中心速度vi(2)使得车体中心速度vc(2)与x1轴有夹角β(2)，旋转半径大小为r(2)。在1时刻时各轮已有夹角θi(1)，为满足刚体运动学关系，各轮中心速度应为vi(1)，且有：

(16)

期望到达2时刻时，中心速度为

vc(2)=[|vc(2)|cosβ(2) |vc(2)|sinβ(2) 0]T

(17)

并有角速度为ω(2)。各轮速度向量可表示为

vwheel(2)=[vc(2)1×4]+[ω(2)1×4]×P

(18)

各轮摆角为

(19)

由于各轮中心速度为vi(1)，不同于x0→x1的变化情况，在该轮系中心速度分配下，x1→x2时车体姿态会发生变化，变化量为ω(1)·t。各轮旋转角速度应表示为

(20)

之后，可根据中心偏距dc与姿态角θc确定预期达到的中心速度vc及角速度ω并持续进行上述调速循环。

2.2 基于驱动能力的控制

轮系驱动能力有限，因此利用两轮速度差消除偏差的纠偏能力是有限的；同时，为保证AGV循迹时流畅运行，应避免出现指令电机频繁正反转、系统带宽不足导致明显停顿的情况。所求解各轮驱动速度应使得对任一viL、viR，满足0≤viL≤vmax且0≤viR≤vmax。当基于偏差状态所得各轮驱动速度不满足上述条件时，应考虑限制车体旋转中心位于车体y轴上。

在适应值选择方面,理论上最理想的适应值应该是重建误差Er,但在实际工程中重建误差是不可知的。这里,距离误差el与重建误差有较高的相关性,在一定程度上能反映重建误差的变化,所以本文以所有重建点的距离误差之和作为粒子群优化方法的适应值。

图9所示为xc<0条件下路径的3种规划。图(a)所示为θc<π/2的情况，定义图(a)所示轨迹为L1类轨迹，该类轨迹可实现姿态与距离的同步纠偏。图(b)所示为θc<π/2条件下优先校正距离偏差的一种轨迹规划，定义图(b)所示轨迹为L2类轨迹，与L1类轨迹相比更适用于中心偏距超出最大允许范围的情况。图(c)所示为θc>π/2的情况，该种情况下应使θc转化至小于π/2的状态以便于向L1或L2类轨迹过渡，定义图(c)所示轨迹为L3类轨迹。xc>0时规划轨迹方式类似，定义为R1、R2及R3。若使用上述两大类轨迹对AGV进行控制，AGV将在各类路径间来回切换，达到循迹运行的效果，如图 10所示。

图 10 各类路径相互转化

设AGV起始时刻状态如图6所示，同时设中心偏距dc超出距离偏差允许范围，为车体规划L2类轨迹。各轮中心速度vi(0)=[vd0 0]T。期望到达1时刻时，在坐标系x1-y1下，中心速度为vc(1)且有旋转半径r(1)，vc(1)与x1轴平行。1时刻车体状态变化见图11。设未知的旋转半径r(1)为rlim，则：

图1 差速轮结构

图4 车体坐标系

图5 偏差状态

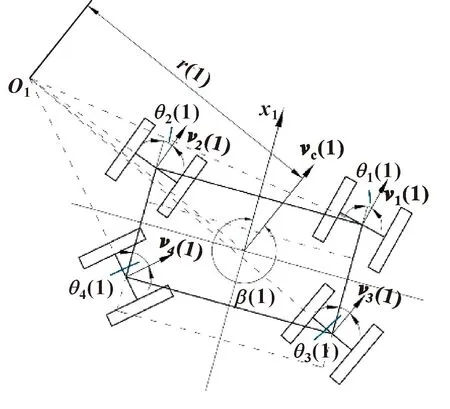
图7 1时刻车体状态

图8 2时刻车体状态变化

图9 L类轨迹规划

(21)

其中：ωsign为控制车体旋转角速度方向的符号量。各轮速度展开可表示为

vwheel(1)=[vc(1)1×4]+[ω(1)1×4]×P=

(22)

上式与式(11)的区别在于，由于rlim是未知的，使用rlim表示的vix(1)、viy(1)也是未知的。各轮摆角、各轮旋转角速度及各轮左、右两轮速度分配可使用式(12)—(15)计算，所求得θi(1)、ωi(0)、viL(0)及viR(0)也均含有未知量rlim。

由于车体中心速度方向与x轴平行，若角速度为顺时针，可确定各轮应有摆角方向，如θ1(1)应为负值，v1L(0)>v1R(0)。解不等式：

(23)

可得满足上述条件的旋转半径rlim，将rlim赋予r(1)并代入式(11)—(15)重新进行速度分配，可得确定的viL(0)、viR(0)、θi(1)和ω(1)。

车体运行一周期后，设1时刻车体中心偏距与姿态角仍满足L2类轨迹规划条件。为车体规划L2类轨迹，即在2时刻时，坐标系下x2-y2下，中心速度为vc(2)且有旋转半径r(2)，vc(2)与x2轴平行。设未知的旋转半径r(2)为rlim，则：

(24)

后续计算方式与前述过程类似，使用式(22)—(23)求解符合条件的旋转半径rlim并将rlim赋予r(2)，重新进行速度分配计算，2时刻状态如图12所示。

图12 驱动能力限制下，2时刻车体状态变化

2.3 混合纠偏策略

基于偏差状态的控制优势在于可稳定跟踪并快速消除误差，最终达到稳定状态。这种控制方法下，线速度、角速度与误差相关，纠偏效率高。但是，方向不定的线速度与角速度组合后各轮摆角方向正负不可预知；若使用不等式限制驱动速度大小和方向，各不等式取值范围可能不存在交集。

基于驱动能力的控制由于限制了车体中心速度方向，使得在角速度方向确定时，轮系摆角方向确定，便于控制车速范围。但也由于限制了车体中心速度方向使得循迹不够灵活，车体中心始终在轨迹线附近摆动。

结合两种方法的优势，可得基于有限纠偏能力的多差速单元循迹协同控制方法。该方法考虑轮系驱动能力和物理结构限制，同时受到位姿偏差约束，最终可实现多差速单元驱动AGV的稳定循迹运行。控制流程可总结如图13所示。为便于描述，将基于偏差状态的循迹控制称为方法一，将基于驱动能力的状态控制成为方法二。

图13 混合控制流程

设起步时刻计数为q，在进行轮系回归零位步骤后，各轮摆角均为0，此时各轮中心速度也为参考速度，即vi(q)=[vd0 0]T。使用ωsign，1、ωsign，2分别表示方法一、方法二的车体角速度指标。使用指标量f表示速度分配使用方法，f=1时表示使用方法一，f=2时表示使用方法二；当车体执行回归零位步骤时，记f=3。

当前时刻车体有距离偏差dc、角度偏差δc和姿态角θc，由此可确定基于方法一的指标量ωsign,1、中心速度方向角β以及基于方法二的ωsign,2。首先使用方法一进行速度一步分配，得到当前时刻各轮左、右轮驱动速度viL(q)、viR(q)，以及下一时刻可得到的摆角θi(q+1)、各轮中心速度vi(q+1)以及车体旋转角速度ω(q+1)，并记ωsign(q+1)=ωsign,1、f=1。若此时有任一viL(q)或viR(q)不满足大于或等于0且小于或等于最大驱动速度的条件，应调用方法二进行速度一步分配并获得相关参数，同时记录ωsign(q+1)=ωsign,2、f=2。各轮系按照驱动速度viL(q)、viR(q)运行，到达下一时刻，此时各轮有摆角θi(q+1)，各轮中心速度应为vi(q+1)。

记q=q+1，使用与前述类似的方法，根据当前时刻距离偏差、姿态角等参数，确定基于方法一的相关指标量并进行轮系速度分配；若有任一轮系驱动速度不符合条件，则使用方法二进行速度分配。与速度一步分配的区别在于，此时速度分配时应考虑车体姿态变动量及各轮中心速度与车体坐标系夹角。若计算所得结果f=2且车体应有角速度旋转方向与上一时刻不同，即ωsign(q+1)·ωsign(q)=-1，这表明各轮摆角方向将发生变化，为保证调姿效率、符合刚体运动条件，应调用轮系回归零位步骤；若不满足上述条件，则令q=q+1并进行正常的步骤循环。

3 仿真结果

记车体结构参数w1=0.9 m，w2=0.8 m；差速轮两轮中心间距的一半dw=0.21 m，指令速度vd=0.5 m/s，轮系最大驱动速度vmax=2 m/s；计数时间间隔t=0.02 s。初始时刻计数q=1，车体姿态角θc(1)=86°，各轮摆角分别为θ1(1)=-14°，θ2(1)=7°，θ3(1)=10°，θ4(1)=-10°。

初始状态可表示如图14(a)所示，此时车体中心与轨迹线距离dc(1)=-0.017 m，与轨迹线夹角δ(1)=4°。设置中心偏距最大允许量dlim=0.02 m，角度偏差最大允许量θlim=2°。仿真步数共计100步，由不同时刻结果及图15、图16可看出车体姿态得到纠正并逐步靠近轨迹线，最终稳定行驶在轨迹线上。在时刻计数q=100时，车体中心偏距稳定在0.01 m，车体姿态角稳定在90.04°。

图14 不同时刻车体相对轨迹线姿态

图15 车体中心偏距dc变化

图16 车体姿态角θc变化

图17为各个计数时刻f数值记录，可看出整个纠偏流程中归零步骤、方法一、方法二交替使用。q=1时由于各轮摆角不一致，首先进行了轮系归零并在计数为3时达到各轮摆角均已归零的状态，即θi(3)=0。

图17 速度分配指标

回归零位后，首先使用方法一计算q=3时刻各轮左、右轮速度，解得：v1L=-0.466 m/s，v1R=1.466 m/s；v2L=-0.654 m/s，v2R=1.654 m/s；v3L=1.466 m/s，v3R=-0.466 m/s；v4L=1.654 m/s，v4R=-0.654 m/s。不满足每套轮系左右轮均不反转且不超速的要求。使用方法二重新计算速度，解得：v1L=0.134 m/s，v1R=0.866 m/s；v2L=0.110 m/s，v2R=0.890 m/s；v3L=0.866 m/s，v3R=0.134 m/s；v4L=0.890 m/s，v4R=0.110 m/s。将上述数值赋予viL(3)和viR(3)，车体在第四时刻拥有摆角θ1(4)=1.998°，θ2(4)=2.131°，θ3(4)=-1.998°，θ4(4)=-2.131°，如图18、图19所示。由于各轮中心速度相同且指向一致，车体姿态并未发生改变，θc(4)=86°，车体中心进一步靠近轨迹线，dc(4)=-0.016 m。

图18 各轮驱动速度

图19 各轮摆角

整个仿真过程按照混合控制方法，对各轮系速度进行了分配。如图18所示，除起步时刻和70时刻进行必要的轮系归零步骤导致轮系反转外，其余时刻各轮均未出现速度小于0或超出驱动能力极限的情况。最终在第70时刻，距离偏差及角度偏差均位于允许范围内，在进行了轮系归零步骤之后，各轮摆角为0(见图 19)并按照指令速度沿轨迹线向前行进，达到稳定状态。

4 结论

(1)基于偏差的控制策略可有效消除偏差并使偏差趋于稳定；基于驱动能力的控制策略考虑实际情况中有限的纠偏能力，为循迹过程提供速度约束。

(2)本文作者提出的基于有限纠偏能力的多差速单元循迹协同控制在充分考虑差速轮运动学特性及整车刚体运动学特性的基础上，将基于偏差的控制策略与基于驱动能力的控制策略相结合。

(3)该方法可有效协调位姿纠偏需求与轮系运动能力。仿真结果表明：该方法下AGV位姿偏差被逐步消除并最终达到稳定状态，实现了差速驱动AGV循迹性能的整体优化。