复式静压箱结构参数对膜片特性影响的研究

田润秋，张宏，孙怡浓，战东毅，马春帅

(1.大连理工大学机械工程学院，辽宁大连 116024；2.中核产业基金管理有限公司，北京 100044)

0 前言

制备锂电池中的隔膜时，经过萃取工序会沾上带有二氯甲烷的液体。隔膜质量直接影响电池的界面结构、内阻、容量等，是电池内部安全性的主要保障[1]，提升隔膜的抗穿刺、自关断、耐高温等性能，有助于提高电池的安全性能和循环使用次数[2]。对隔膜进行干燥是保障产品质量的重要工序，对隔膜表面性能有重要影响。目前，成膜的光泽度和透明度差异是较大的质量问题[3]，而风场内部的均匀性以及干燥效果直接影响膜片的质量与性能，并且复式静压箱各结构参数直接影响干燥质量。合理设计复式静压箱各结构参数，对于提高薄膜的表面质量和力学性能以及指导现场生产有重要意义。

目前，国内外的一些学者对热风干燥技术、静压箱效果影响因素以及干燥效果机制进行了相关研究。在干燥效果方面：刘卫涛等[4-5]通过在隧道式干燥设备内干燥纸浆，探讨了热风温度、热风速度和纸张厚度对纸浆干燥过程的影响。徐景端和李英葆[6-7]提出导流板、均压孔板、截面异形、喷口调节板等是能提高出风均匀性的结构措施。在静压箱方面：英国的JANGAM等[8]通过试验和进行三维流场仿真的办法分析静压箱，发现预分布器距主静压箱体的距离和鲍尔环填充都会影响气流均匀性。德国MIREK等[9]发现箱体结构不对称会在流化床内生成死区并造成送风不均，通过在各送风通道之间设置挡板并装置带有可变直径孔的隔板可有效改善这一现象。ZHANG等[10]提出了一款带渐扩型孔板的静压箱机组设计，对送风量进行预设，实现平衡风速以及节能的效果。但是上述研究应用在生产过程中仍然出现静压箱出风均匀性波动较大的情况。

本文作者在前人研究的基础上，使用数值模拟研究复式静压箱内部流场分布，通过试验研究，验证数值模型的准确性；在此基础上，利用数值模拟的方法分析复式静压箱各结构单因素对出口速度均匀性的影响规律，并对静压箱进行结构优化，得到复式静压箱结构设计的最优方案。

1 计算模型

1.1 物理模型及结构参数

干燥房内部结构如图1所示，因此，对膜片干燥过程的分析以及对复式静压箱各结构参数的调整及控制，就显得尤为重要。

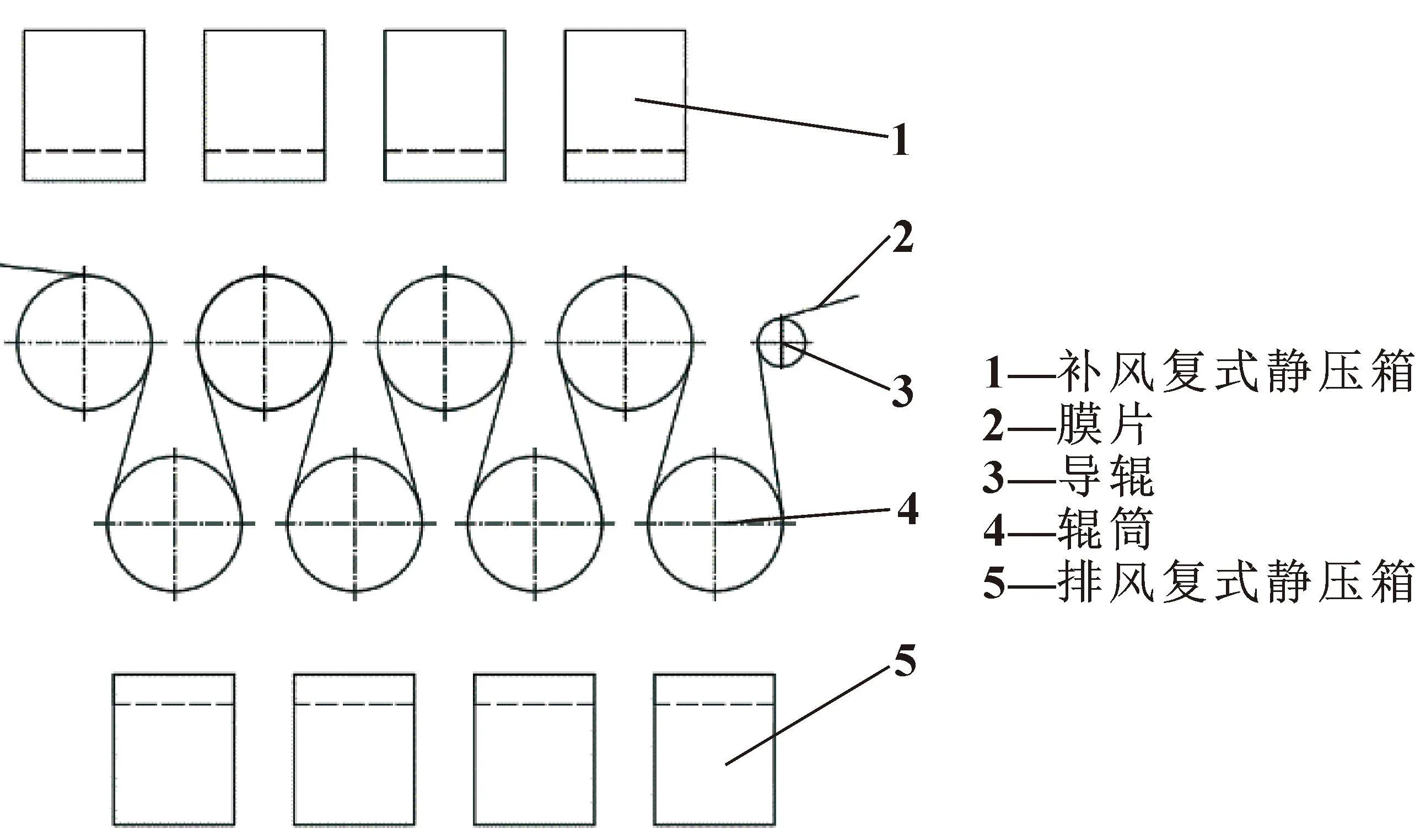
图1 干燥房内部复式静压箱工作示意

此研究所采用的模型为复式静压箱，其装配体由一次静压箱及二次静压箱构成，如图2所示。一次静压箱截面设置为矩形，干燥热风通过送风管道进入一次静压箱，经过静压后从一次静压孔板进入二次静压箱，经过二次静压后由二次静压孔板排出，吹至膜片表面。其中，一次静压箱的尺寸为400 mm×400 mm×3 800 mm，二次静压箱的尺寸为400 mm×100 mm×3 800 mm。

图2 复式静压箱模型

1.2 流体流动方程及传热控制方程

在生产线中，热风吹到膜片上干燥的过程是稳定状态时，外部环境参数也趋近于稳定，复式静压箱与膜片的温度场仅在很小的范围内周期性波动，此时可以认为复式静压箱、膜片和内部热风的干燥过程是稳态传热。流体流动满足质量守恒、动量守恒以及能量守恒定律，Fluent 的仿真过程可以视为在连续性方程、能量守恒方程、动量守恒方程控制下的流体流动过程的数值模拟[11-12]。

在复式静压箱三维的稳态传热过程中，整个干燥过程达到解决任何流动问题的首要条件就是流动需要遵循质量守恒定律。质量守恒定律具体指在任意时间间隔内，流入流体单元内的质量应该恒等于这一时间间隔内从该单元流出的液体质量。根据质量守恒定律可得质量守恒方程，又称连续性方程[13]，表达形式如(1)所示：

(1)

式中：u、v、w分别为流体速度矢量在x、y、z方向的分量；ρ为流体密度；t为时间。

根据热力学第一定律：热力系内物质的能量可以传递，其形式可以转换，在转换和传递过程中各种形式能源的总量保持不变。

其能量守恒方程[14]如式(2)所示：

(2)

式中：Cp为比热容；T为热力学温度；k为流体传热系数；ST为流体的内热源。

选择合适的湍流模型对复式静压箱数值模拟结果的准确性至关重要[15]。热风在复式静压箱中以湍流的方式运动，选用Standardκ-ε湍流模型，此模型对于壁面边界层、自由剪切流、低雷诺数流动有较好的适应性，对风场模拟、混合层流动等有较好的预测，使得文中仿真模拟数据更加接近真实值，有良好的实际指导意义。

1.3 网格模型与无关性验证

经过对多种划分方法进行大量试验后发现，在保证网格质量与计算精度前提下，为保证所划分的网格具有较高的质量、确保数值计算的速度和精度，划分网格时将装配体模型分割成几个规则的子块，分别对一次静压箱、二次静压箱和外部空间 3个模块进行网格划分，如图3所示。整体用多面体网格划分，其中，二次静压箱作为关键的研究部分，对它进行了适量的网格加密，得到网格单元数为1 809 524，节点数为3 597 549，平均畸变度为0.204，网格质量较好。

图3 网格划分

对划分好的网格进行简化并做网格无关性验证，简化后的网格单元数为442 737，是原网格的0.24；节点数为1 396 634，是原网格的0.38；平均扭曲度为0.22，稍差于原网格，但它低于0.25，仍处于质量良好范围。通过仿真计算可得两者风速曲线相似度极高，为减少计算时间和计算资源，简化网格进行数值计算。

1.4 边界条件及参数设置

根据工程实际需求，复式静压箱入口采用的边界条件为速度入口，速度为2.64 m/s，温度为323.15 K，出口边界条件为压力出口，出口压力为标准大气压，膜片初始温度为300 K。

在软件中，采用稳态计算方式，考虑到介质为空气，与SIMPLE、SIMPLEC、PISO相比较，压力速度耦合采用更加稳定精确的Coupled算法，压力插值法选择Standard格式，湍动能和湍流耗散率的离散格式均取二阶迎风格式。

2 计算结果分析

2.1 复式静压箱干燥过程的风速分析

运用上述CFD方法对复式静压箱进行数值模拟仿真研究。在图4及图5中，气体分别从左进口和右进口同时进入静压箱。一次静压箱中心区域远离入口，速度明显降低，且速度方向从水平方向开始向竖直方向过渡。膜片表面受到的干燥热风呈现两边高、中间低，并且中间处速度波动较大。气体方向基本上以竖直方向为主，孔板内流动可以理解为气体以一定速度进入二次静压箱，如果孔板厚度足够厚，那么气体经过一定长度后其速度方向将改变为沿着圆孔的轴线方向(图4所示Z方向)，有利于气体在二次静压箱结构中以垂直于出口平面的速度方向膜片进一步均匀发展，从而提高出口处速度均匀性。

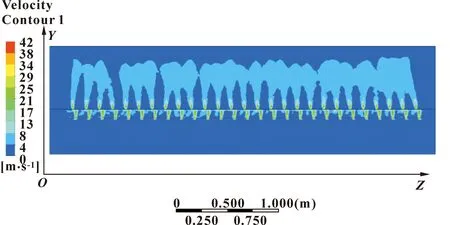
图4 复式静压箱干燥过程X平面风速场云图

图5 复式静压箱干燥过程辊筒母线速度曲线

但是由于孔板质量和经济性制约，厚度不能太大，故气体很难在孔板内有充分的距离调整方向，改变气流方向的作用不能完全体现出来。所以在理论模拟中将探究孔板的最小厚度转变为孔口引风管长度，既能满足改变气流方向的作用，又能满足工程实际要求。

2.2 单因素数值模拟

在上述辊筒母线两端各去除200 mm长度的数据点(考虑切边工艺)，在每条线剩余部分上均匀地取100个点，记录其温度值，计算出的CV和CT分别表示达到稳态后膜片表面的速度均匀性及温度均匀性。

在相同入口速度或相同射流雷诺数条件下，不同结构下膜片的表面换热系数h存在差异。为量化各结构的风速均匀性和温度均匀性表现，定义其离散程度如下：

(3)

式中：σV为速度的标准差；μV为速度的平均值。CV值越小对应的均匀性越好。

(4)

式中：σT为温度的标准差；μT为温度的平均值。CT值越小对应的均匀性越好。

为研究复式静压箱中二次静压箱高度Y对膜片干燥效果的影响，分别在Y=80、90、100、110、120 mm的条件下对复式静压箱进行数值模拟。图6为速度均匀性和温度均匀性随二次静压箱高度变化曲线。可知：速度均匀性及温度均匀性都随着高度的增大呈现更均匀的趋势，速度均匀性表现虽然更好，却不明显，在二次静压箱高度为80～100 mm左右温度变化较明显。这是因为二次静压箱在一次静压箱的基础上再一次对热风进行了静压，将动能转化成压能，使均一性更好。

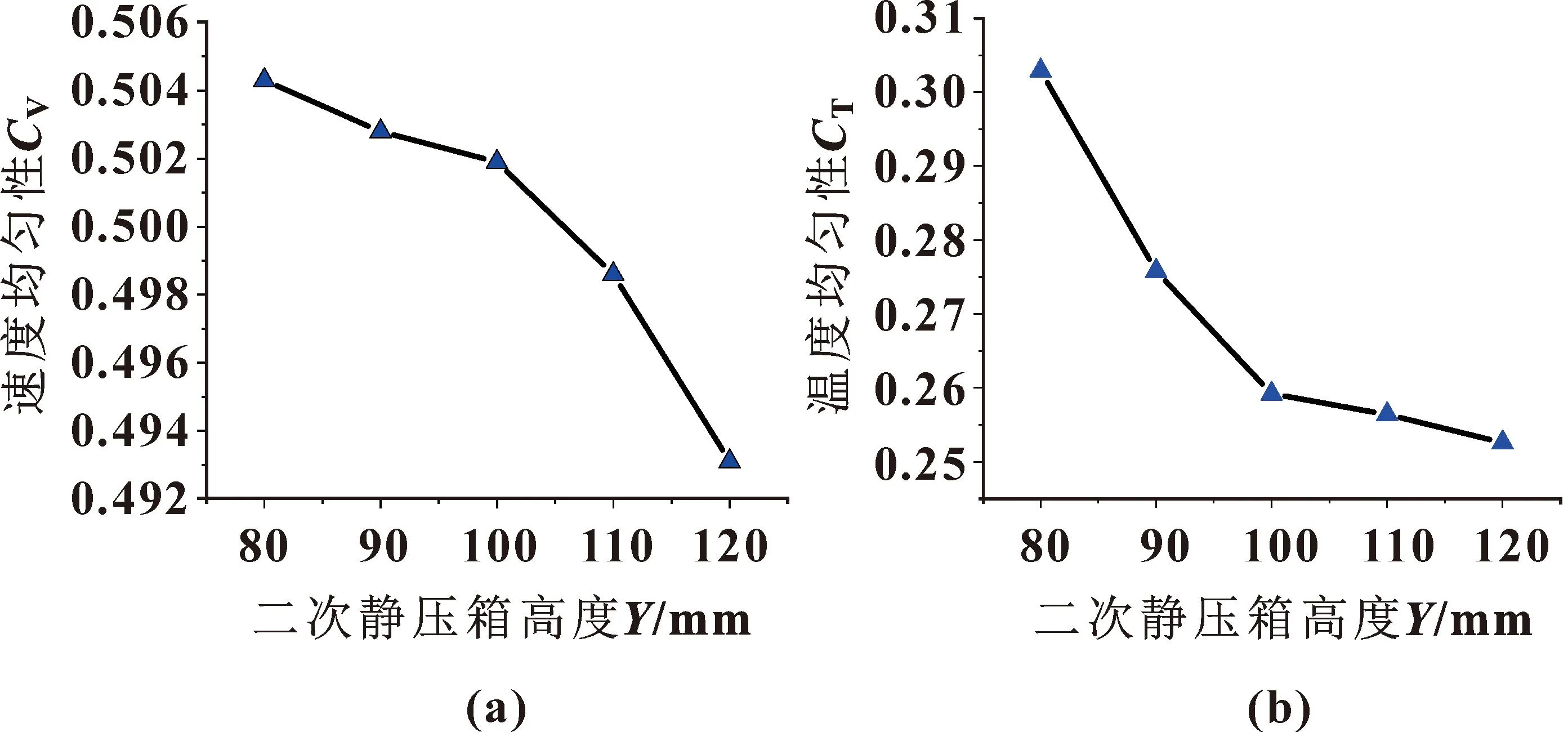
图6 速度均匀性(a)和温度均匀性(b)随二次静压箱高度变化曲线

为研究静压箱宽度H对膜片干燥效果的影响，分别在H=360、380、400、420、440 mm的条件下对复式静压箱进行数值模拟。图7为速度均匀性和温度均匀性随风量变化曲线。可知：随着静压箱宽度的增大，风速均匀性明显变好，温度均匀性变差，但是其值变化很小。这是因为随着静压箱宽度的增大，静压箱内部流道横截面积增大，静压箱内部流速变慢，形成了更好的静压效果，所以膜片风速均匀性明显提高。

图7 速度均匀性(a)和温度均匀性(b)随静压箱宽度变化曲线

为研究引风管长度L对膜片干燥效果的影响，分别在L=4、6、8、10、12 mm的条件下对复式静压箱进行数值模拟。图8所示为速度均匀性和温度均匀性随引风管长度变化曲线。可知：速度均匀性在引风管长度为8 mm时表现最好；温度均匀性随着引风管长度的增大呈现更均匀的趋势，温度均匀性表现虽然更好，却不明显，在引风管长度为8 mm左右温度变化较明显。这是因为增加了引风管，给了静压箱内部风出口一个缓冲的区域，使得风速更加均匀，但是引风管长度不能一直增长，在8 mm左右表现最佳。

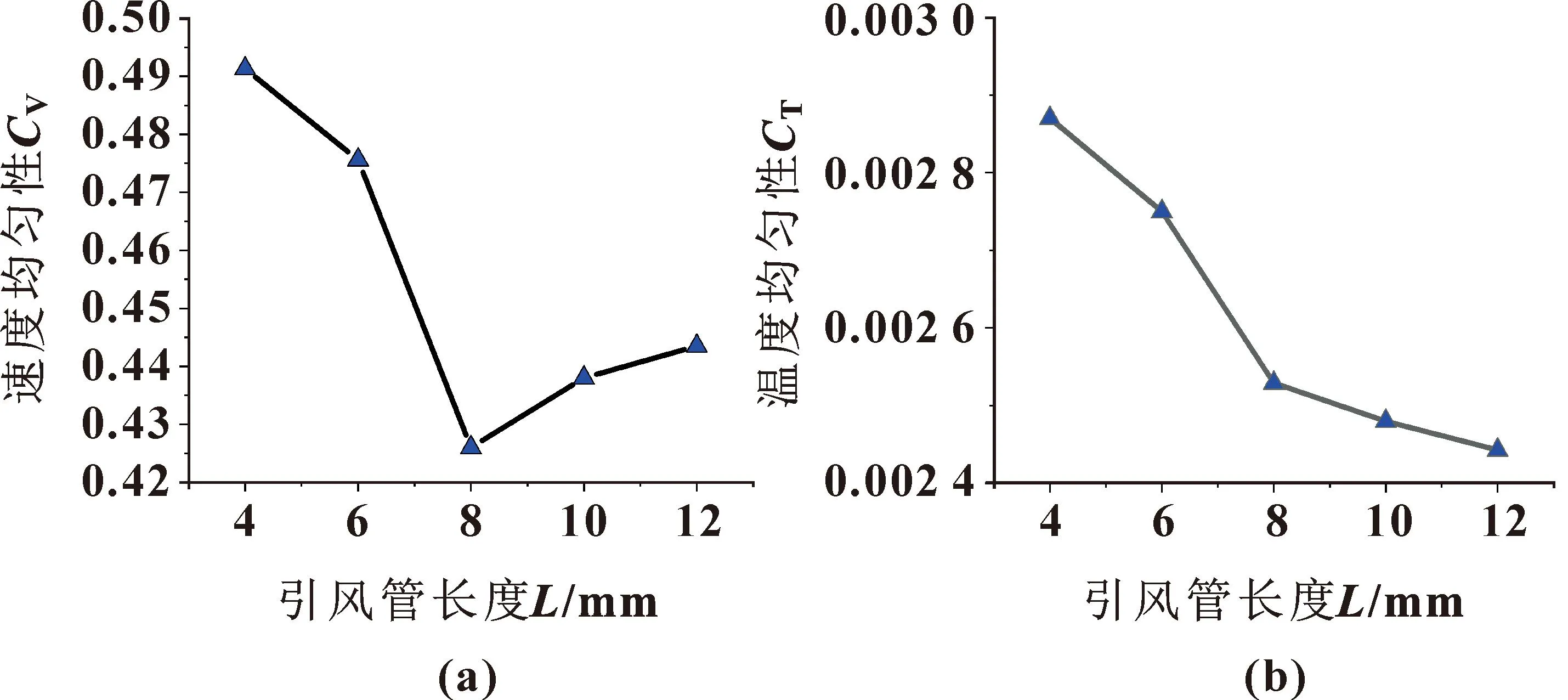
图8 速度均匀性(a)和温度均匀性(b)随引风管长度变化曲线

为研究孔板错位距离Δs对膜片干燥效果的影响，分别在Δs=0、16、32、48、65 mm的条件下对复式静压箱进行数值模拟。图9所示为速度均匀性和温度均匀性随孔板错位距离变化曲线。可知：速度均匀性在错位距离为32 mm时表现最好。温度均匀性都随着引风管长度的增大呈现更不均匀的趋势；这是因为上下孔口有错位距离，在热风通过第一层孔板时有一个角度，并不是垂直于孔板，在错位距离为32 mm时，风速均匀性更好，说明这个位置更加靠近吹出一次静压箱后的角度。

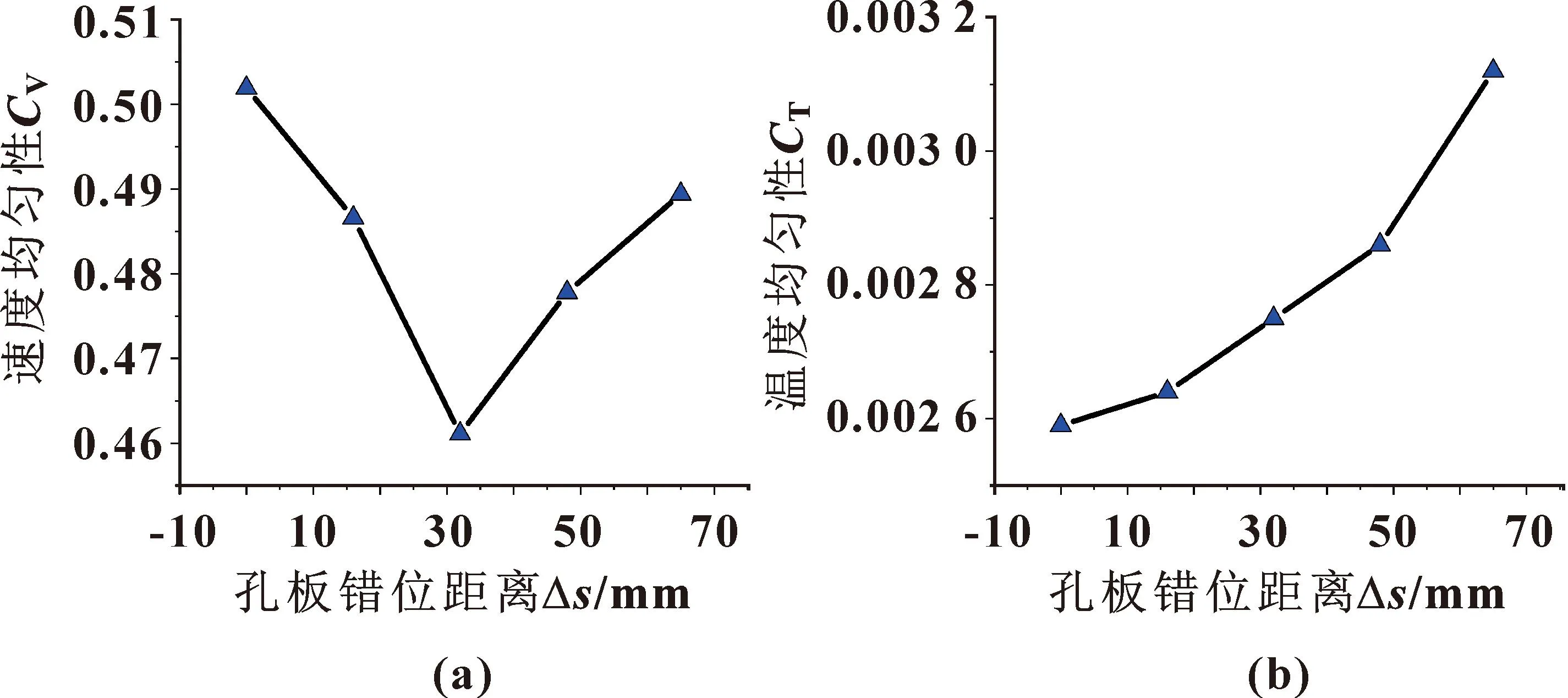
图9 速度均匀性(a)和温度均匀性(b)随孔板错位距离变化曲线

2.3 多因素正交设计仿真

利用 Design-Expert 10.0 软件，对静压箱宽度、引风管长度和二次孔板与一次孔板错位距离3个因素进行了分析及结构优化。选取距离复式静压箱300 mm处(膜片母线)、X方向的一条直线处的平均风度及温差方差作为优化目标，建立正交试验表对静压箱干燥效果进行数值模拟。因素水平设计如表1 所示，仿真试验结果如表2所示。

表1 因素与水平设计

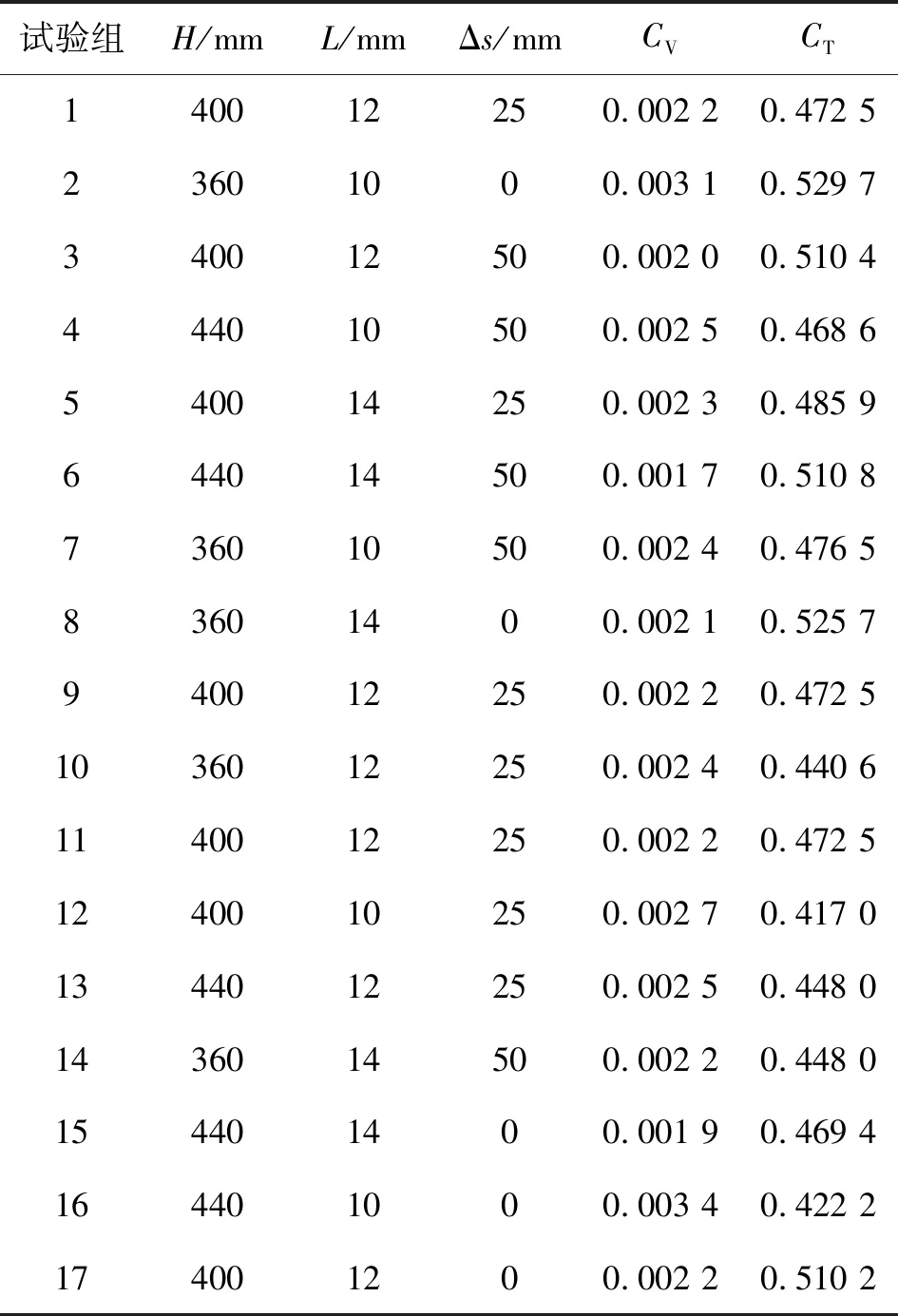
表2 正交设计仿真结果

根据数据样本，得到温度均匀性和速度均匀性的二次回归模型：

CV=0.47-0.01H-0.013L+0.015HL+0.027HΔs-

0.003 67LΔs-0.02H2-0.013L2+0.046Δs2

(5)

CT=0.002 25-0.000 012 4H-0.000 399L-

0.000 178Δs-0.000 134HL-0.000 048 4HΔs+

0.000 197LΔs+0.000 131H2+0.000 206L2-0.000 17Δs2

(6)

式中：H为静压箱宽度；L为引风管长度；Δs为二次孔板与一次孔板错位距离；CV为速度均匀性；CT为温度均匀性。两模型的决定系数R2与校正决定系数分别为 0.895 6、0.949 3，均接近1；变异系数与精密度分别为3.48%和6.02%、8.473和14.007，说明2个拟合回归模型具有较高的可靠性。

考虑到静压箱在实际生产的情况，针对回归模型，运用Design-Export 10.0软件中的 Optimization 功能，以速度均匀性及温度均匀性最好为条件，求解回归模型得到均匀性最优结构参数为：静压箱宽度为473.113 mm，引风管长度为16.229 mm，二次孔板与一次孔板错位距离为0 mm。此时优化后的温度均匀性为0.001 91，风速均匀性为0.416 9，优化后的温度均匀性值与风速均匀性值较最初值(温度均匀性0.002 59，风速均匀性0.501 9)分别降低了0.000 68(26%)和0.085(17%)。

2.4 交互响应面分析

根据回归模型结果，利用Design-Expert 10.0进行各个因素交互响应面的绘制。静压箱宽度与引风管长度、静压箱宽度与二次孔板与一次孔板错位距离、引风管长度与二次孔板与一次孔板错位距离对膜片表面温度均匀性的交互响应面如图10所示。当静压箱宽度增大时，温度均匀性值呈先减小后增大的趋势；当引风管长度和开孔错位距离增大时，温度均匀性值都减小。静压箱宽度与引风管长度、静压箱宽度与二次孔板与一次孔板错位距离、引风管长度与二次孔板与一次孔板错位距离对膜片表面速度均匀性的交互响应面如图11所示。当静压箱宽度增大时，速度均匀性值呈先增大后减小的趋势；当引风管长度增大时，速度均匀性值增大；开孔错位距离增大时，速度均匀性值呈先减小后增大的趋势。

图10 温度均匀性的交互响应面

图11 速度均匀性的交互响应面

3 结论

(1)通过数值模拟仿真分析可知，在干燥热风进入静压箱干燥膜片的过程中，在膜片的母线方向上，风速场呈现出中间低两端高且中心位置风速波动较大的现象；

(2)通过单因素仿真试验可知：膜片表面的风速均匀性随着二次静压箱高度和静压箱宽度的增大呈现更加均匀的趋势，随着引风管长度和不同孔板错位距离的增大呈现先均匀后紊乱的趋势。除此之外，膜片表面的温度均匀性随着二次静压箱高度和引风管长度的增大呈现更加均匀的趋势，随着静压箱宽度和不同孔板错位距离的增大呈现逐渐紊乱的趋势；

(3)通过对静压箱宽度、引风管长度、二次孔板与一次孔板错位距离的正交设计仿真，以速度均匀性及温度均匀性最好作为优化参数指标，建立回归模型，求解并圆整后得到最优参数组合为：静压箱宽度 为473 mm、引风管长度为 16 mm、二次孔板与一次孔板错位距离为0 mm。此时优化后的温度均匀性为0.001 91，风速均匀性为0.416 9，优化后的温度均匀性值与风速均匀性值较最初值分别降低了26%和17%。

综上所述，文中在普通静压箱的基础上提出了复式静压箱的结构，并且结合工程实际应用，针对复式静压箱的结构参数进行仿真验证及优化设计，提高了干燥房内部干燥热风的速度均匀性和温度均匀性，为接下来的产线设计提供了理论基础。