基于校园供水系统智能管理的建模研究

朱军伟, 顾丽娜, 李 蕊, 兰彩霞

(1.杨凌职业技术学院, 陕西 杨凌 712100; 2.甘肃政法大学, 甘肃 兰州 730000)

0 引 言

近年来,高校校园用水需求量逐年增长,这对于校园供水系统智能化的精准管理颇具挑战。一方面,校园供水系统是否正常运行将会直接影响水资源的节约程度。另一方面,校园供水管网一旦出现老化、破损,漏水情况随之增加,尤其是地下管道的漏损不易发现且实施及时维护。故通过数据处理与分析,掌握各个时间段,各个功能区的用水情况,及时发现和解决智能供水系统中存在的问题,对于维护管道和节省维修、材料成本等起着尤其重要的作用[1-3]。基于此,可以通过数据处理分析和构建数学模型进一步优化校园供水系统,以期提升校园供水系统智能化管理水平。本文依据某高校2019年全年水表的层级关系以及所有水表四个季度的读数[4],利用已知数据首先对不同功能区的用水特征进行探讨分析,表征不同区域的用水特征,进而通过建立傅立叶函数对水表层级关系进行误差分析,确定水管漏损位置。在调查市场水价、管网维修成本的基础上,构建校园管道维护更新决策模型,从而实现校园供水系统智能化管理。

1 校园不同功能区用水特征分析

1.1 数据预处理

主要考虑水表在2019年1-12月份中每月的变化规律,将数据导入到Spss24.0中进行筛选,剔除异常点。事实上,各季度都有部分数据发生偏离(即异常点),故需剔除异常数据,并将其重新归类,现绘制出一级水表在1-12月用水量的变化折线图,见图1。

图1 用水量变化折线图

显然,1-2月之间的用水量(即水表数据)出现较为明显的下降,预计学生离校,导致用水量减少;2-4月用水量出现大幅度上升,表明学生已逐渐回校,使其短时间内校园用水量出现短暂的大幅提升;4-5月校园卫生基本已清理完毕,导致用水量出现一定量的减少;随后的5-6月出现回升,即随着天气加热,学生洗澡的频率及饮用水等方面有一定提升,使得用水量出现小幅度回升;而6-9月因高温天气的到来,大家也因暑假暂时性离校,所以校园用水量出现一段时间的平滑期;9-12月天气逐渐变冷,对热水的需求也急速提升,导致用水量出现一定趋势的上升,随后到达10月时,保持相对平滑,在小范围内波动。

综上可知,每月的用水量都有波动,为此需要从其波动的趋势聚类划分功能区,并探寻不同功能区的用水特征。

1.2 功能区划分

基于以上结论,为探究校园内不同功能区的用水特征,结合实际数据及各功能区的具体特征[5],将各水表按照功能区进行聚类划分。划分结果具体见表1。划分依据着重考虑以下方面:

表1 各功能区的聚类划分明细

(1)功能一致的归为一个功能区;

(2)名称接近的归为一个功能区;

(3)隶属于一栋大楼区域的水表归为同一个功能区;

(4)部分水表无法从名称判断功能及一级总水表不能划分到某特定功能区的舍弃。

结合各功能区的聚类划分结果,可得出水表层级的隶属关系,为使得各功能区水表用水特征表现明显,现使用Matlab软件作出部分功能区的用水特征图,以期从特征图中得出用水量波动的具体时间及基本趋势,为功能区的划分提供详实依据。因考虑到校园用水实际情况与水表数据的稳定性,这里只研究四大重点功能区域:后勤设施、办公楼、教学楼、宿舍。其余非重点功能区研究方法类似,不再赘述。现就四大功能区的用水特征图做出分析,见图2。

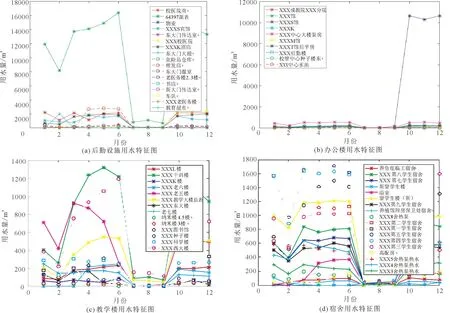
图2 后勤设施、办公楼、教学楼、宿舍四大功能区用水特征图

由图3可得出如下结论:后勤用水设施中,危险品仓库用水量波动范围最大,在1-6月之间预测为对仓库进行大面积的清洗,以及安全性的处理,导致用水量出现上升趋势,而7-12月,危险品入库后,至于存放状态,所以用水量出现巨幅下降。

办公楼用水量整体呈现平滑的趋势,但其在9-12月用水量出现大幅度的上升,XXXK楼可能为工业楼,在9-12月这时间段中工业生产导致工业用水量出现大幅度增长。

教学楼的用水特征较为一致,其中XXX干训楼与XXX西大楼两组数据在整体走势上保持一致,在6-7月期间的用水量几乎接近,所以预测其XXX西大楼与其XXX干训楼同为培训楼,在2-6月之间培训量的加大以及培训人员的增加,导致用水量增加。

宿舍用水量用水较为集中,放假期间用水量大幅下降,开学之后,用水量大幅上升。

2 水表层级关系模型建立

2.1 模型建立

在上述不同功能区用水特征分析的基础上,对各个水表进行层级归类,运用Matlab软件中的工具箱对其数据进行拟合,以此建立有关各级表层数据关系的傅立叶函数模型。

一级、二级、三级、四级水表层级用水量按月变化的拟合曲线见图3。

依据图3拟合曲线,可得相应的傅立叶函数模型,考虑到四级水表层级关系基本一致,故只给出一级水表层级表达式:

y1=1.842×104+1.036×104cos(1.136x)-4815sin(1.136x)+1958cos(2.272x)+64.09sin(2.272x)-4047cos(3.408x)+3175sin(3.408x)+553.4cos(4.544x)+3211sin(4.544x)-1681cos(5.68x)-8481sin(5.68x)

上述傅立叶函数模型表明:水表层级之间联系紧密,但不难看出,数据波动范围依然较大,下面对这一结果做误差分析。

2.2 误差分析

依据上述函数模型,将1-12月水表层级数据分别代入,求出各层级每月的模拟用水数据,与实际值进行比对,如表2所示。

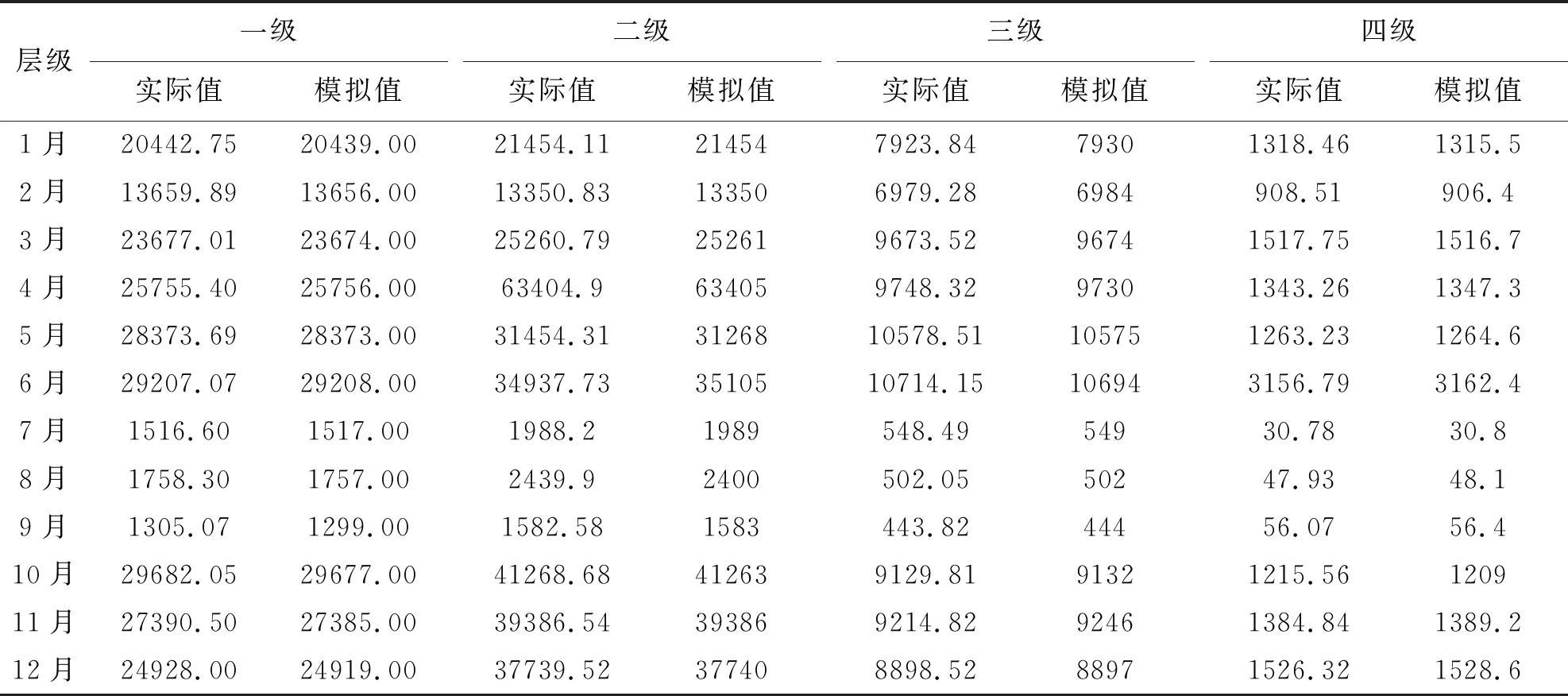
表2 各层级拟合模拟值

对比真实值与模拟值,利用Spss24.0找出误差值,见图4。

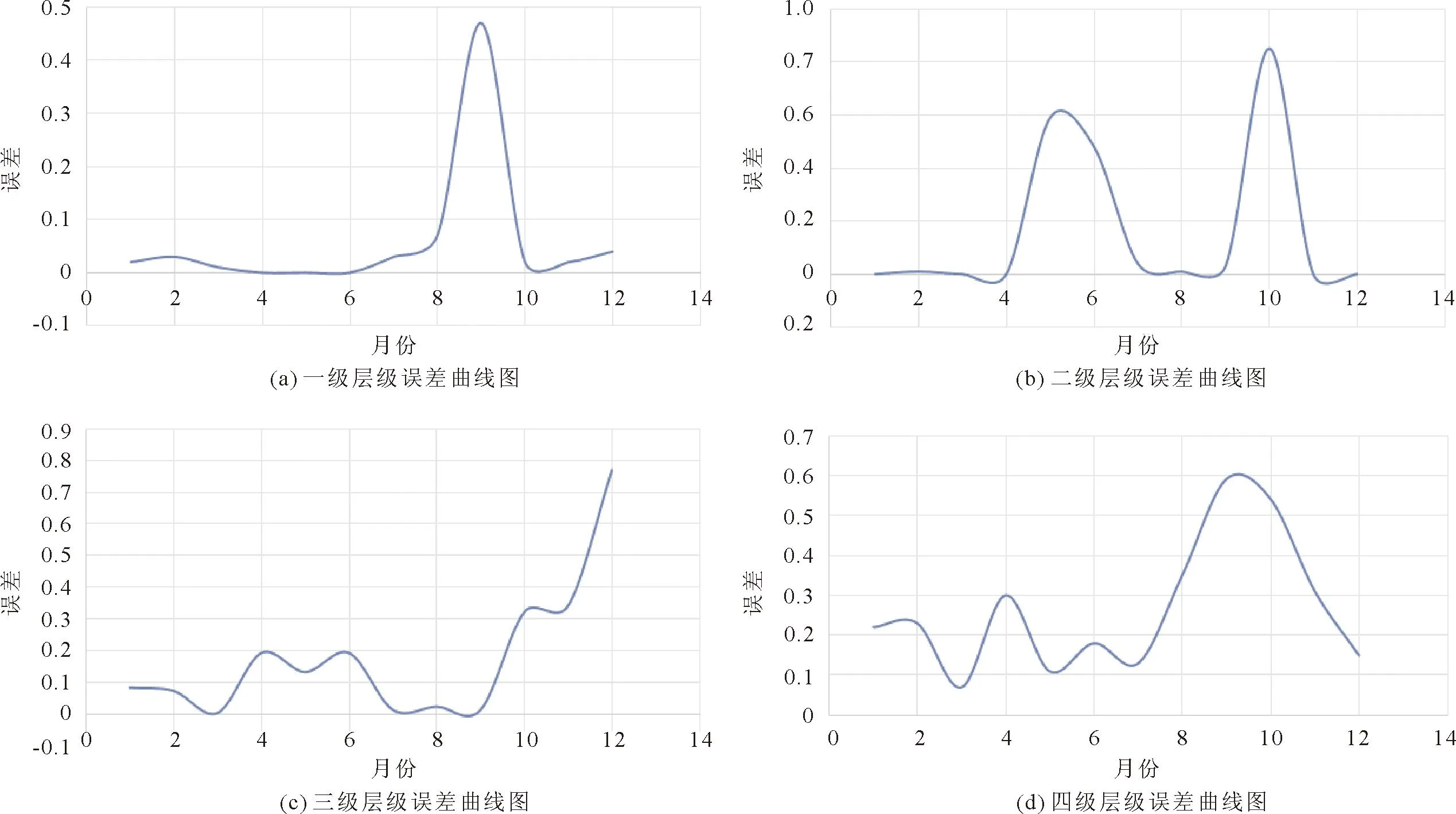
图4 水表层级误差曲线图

显然误差低于10%,认为模拟效果较好,表明建立的函数模型较为合理。

3 供水管网漏损分析

依据水表层级函数模型可知,存在部分异常数据,表明校园供水管网确实存在漏损情况,且管网漏损涉及诸多因素。本文着重研究管道口径与漏损量的关系,利用Excel工具箱进行数据处理,步骤如下:

Step1:计算出实际水表读数(实际水表读数=当前读数-上次读数);

Step2:利用IF(TEXT(G1,“0.000”)=TEXT(F1,“0.000”),“相同”“不同”)筛选出实际水表读数与用水量不同的数据(即漏损量);

Step3:剔除不符合实际的数据(用水量>实际水表读数);

Step4:分别筛选出口径为15、20、25、40、50、80、100、150、200的水表,分别计算其漏损量,并做直方图进行观察。

在数据处理的基础上,下面将不同管径下的漏损量做一统计,如表3所示。

表3 不同管径下的漏损量

从表3发现,小口径管道漏损量较大,其漏损率远远高于大口径的漏损率。为了进一步直观性地验证该结论,所做直方图见图5。

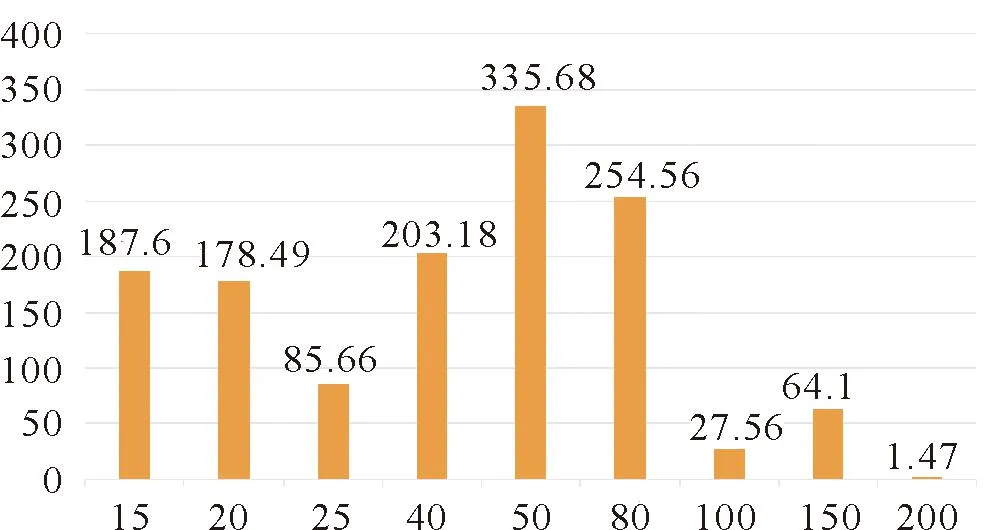
图5 不同管径漏损量直方图

结论显然成立,据此表明:口径越小,漏损越多;反之,漏损越少。一旦明确漏算量较大的管径,则亟需对该管道展开检漏与维修。

4 校园供水管道维护决策方案

校园供水管道漏水,对于其检漏与维修相当重要。供水管网的维修方案一般需要统筹考虑以下几方面:(1)维修管道的费用(含人工费、材料费等)。(2)已经漏水损失的费用(含漏损水量营业损失费用、水污染引发损失费用、漏水浸泡物品的损失费用)。(3)管道的查漏投入费用。故据此最终确定最优维护决策方案。

4.1 漏水损失的费用

结合实际情况,对于维修管道的费用和查漏投入费用可正常处理,故本文只对漏水损失的费用进行详细探究。漏水损失的费用w1可用如下公式表示:

作为岭南地区千年古都的历史名城，广州从秦朝开始，先后定名为任嚣城、番禺城、兴王府以及后来的广州城，历经两千多年。在中国的历史上，岭南地区先后经历了南越国、南汉国两个割据王朝，统治时间接近两百年，在这些王朝的统治过程中留下不少让人赏心悦目的皇家园林艺术。

w1=w11+w12+w13=k1QtT+w12+w13=k1qN[k(t)+s(t)]tT+w12+w13

其中:w11为漏损水量营业损失费用;w12为水污染引发损失费用;w13为漏水浸泡物品的损失费用;k1为水价系数;tT为管道漏水起止时间;Q为漏损量;q为不同口径漏损的单位漏水量;k(t)+s(t)为相同管上不同口径的流量时间和;N为相同口径的管道个数。

上式要注意的是校园供水管道随着使用年限的增大,其漏水概率必然越大,故k(t)+s(t)会随着t的增大而增大。此外,口径大小的不同漏损费用也是不同的。

为方便计算,漏水浸泡物品的损失费w13按w12的15%计算。故管网漏损的最优模型为:

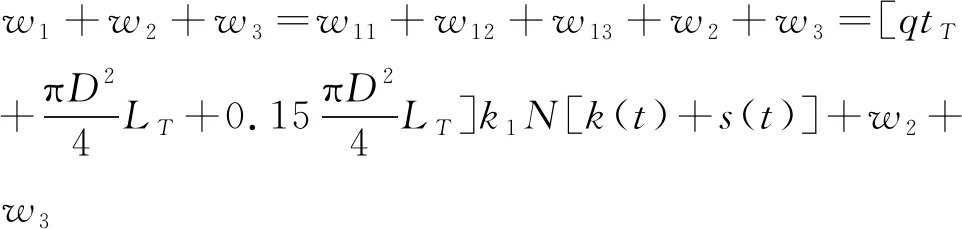
其中:w2表示维修管道的费用;w3表示查漏投入的费用。

4.2 管道维修决策方案

考虑经济决策为目标,构建供水管道维修决策方案。具体如下:

(1)当w1+w2>w3时,经济效益低,成本太大,决策方案最差,但仍需维修供水管道,故在考虑维修的同时一定要做好后期管道维护。

(2)当w1+w2

(3)当w1+w2=w3时,达到经济效益的平衡点,决策方案有待考量,意味着查漏投入的费用可用于维修管道和补偿损失,但一旦出现大面积供水管道漏损,将产生次灾害,故建议慎重选择。

5 结 论

本文基于某高校水表层级关系及四季度数据的变化趋势,通过数据清洗与挖掘,着重解决了校园供水系统智能管理中功能区域的划分及用水特征探究,并对供水管道的漏损情况做了分析,提出可供参考的维修方案,该模型经济效益合理,决策方案可行。同样该模型可推广到具有水表层级、电表层级、燃气层级关系的问题上,且对于当下节约资源具有较好的实用价值。