长大深埋高铁隧道三维地应力场反演方法及应用——以银河山隧道为例

李 鹏 袁 维 张光明 王钦刚 李国圣

(1. 中国铁路设计集团有限公司,天津 300308; 2. 城市轨道交通数字化建设与测评技术国家工程研究中心,天津 300308;3. 石家庄铁道大学土木工程学院,石家庄 050043)

引言

在长大深埋隧道的设计和施工过程中,准确评估隧道区域岩体的初始地应力场对隧道设计和施工至关重要。 根据初始地应力场分布特征设计合理的开挖方案以及支护方式,可有效防止岩爆、大变形、塌方等事故的发生[1-3]。 在工程实践中,难以直接测量隧道开挖影响区域内各点全部的地应力,只能通过水压致裂等方法测出若干关键测点的地应力,然后采用相应的数学方法按照“点→线→体”的思路对隧道影响区域内的地应力进行预测,以获得初始地应力场的大致分布规律,为工程设计和施工提供指导。 这种获取地应力分布规律的方法被称为地应力反演[4-6]。

地应力反演方法有很多种,目前应用较广泛的方法有应力回归分析法[7]、边界荷载调整法[8]、应力试算法[9]等。 已有学者进行相关研究,张敏等采用应力试算法确定模型加载的边界条件,并结合FLAC3D 分析得到桑珠岭隧址区范围的初始地应力场[10];张晨等对BP 神经网络进行优化,结合数值模拟和现场数据,反演计算实际工程的地应力状态[11];王志云等采用线性方程组和线性回归相结合的数学方法,通过数值模拟和现场数据验证该方法的可靠性[12];刘春康等建立某隧道三维数值模型,并基于多元线性回归法反演获得该隧道轴线处的初始地应力场[13];徐安等基于实测数据反推得到浩吉铁路九岭山隧道和桐木隧道初始应力场应力边界条件,并通过数值模拟方法获得初始应力场分布特征[14]。

以某高铁银河山隧道为研究对象,建立其三维数值分析模型,设定多组非线性荷载边界条件模式样本数据库,通过数值模拟方法获得地应力实际观测点的地应力值,将边界条件数据和地应力计算值分别作为输入和输出样本,通过BP 神经网络进行训练,并结合遗传算法寻优功能得到地应力实测数据对应的最优应力边界条件,将该边界条件输入到银河山隧道的三维数值分析模型中进行正算,获得该隧道模型的三维初始地应力场。 此外,采用多元线性回归分析方法对该隧道地应力进行反演,并与上述反演结果进行对比验证。

1 基本原理

1.1 神经网络基本简介

神经网络为模拟人类大脑神经系统的一种信息处理系统,该网络由许多神经元组成,用于大量数据信息的学习和处理,通过对输入、输出样本的自学习,并进行网络结构和连接权值训练修正,从而建立复杂的非线性预测模型,达到对新输入数据进行预测的目的[15-16]。

BP 神经网络是一种广泛应用于工程领域的模型,其算法是将一组样本的输入、输出变成非线性优化问题,通过调整BP 网络中的连接权值、网络规模使实际输出和预期输出之间误差的平方最小,从而实现任意精度逼近任何非线性函数。 按照层次构造,BP 网络包含一个输入层、一个输出层和一个或多个隐含层,神经元只和与该层紧邻的上、下层的各神经元连接,BP 网络结构结构见图1。

1.2 遗传算法基本简介

遗传算法效仿生物的进化、遗传过程而提出的随机搜索方法,即从某一初始值群体出发,经过生存竞争→优胜劣汰→适者生存的过程,基于复制、杂交、变异等操作手段,不断迭代演化逼近最优解,直到实现全局最优。遗传算法包含编码、初始群体的生成、适应度评估检测、复制、杂交、变异共6 个基本步骤,流程见图2[17-18]。

图2 遗传算法计算流程

2 工程概况

某高铁银河山隧道进口位于河北省保定市阜平县,出口位于山西省忻州市,穿越太行山脉剥蚀中山区,全长12 549.74 m。 为了探明该区域地应力状态,在隧道主轴线上钻孔,钻孔深度为290 m,静水位9.6 m,钻孔直径78 mm。 在孔内116~220 m 深度内选定了4 个测试段,深度分别为116.50 ~ 117.10 m、130.20~ 130.80 m、148.00 ~ 148.60 m 和161.70 ~162.30 m。 根据水力压裂的基本原理,通过计算得到最大水平主应力值(SH)和最小水平主应力值(Sh);此外,垂直应力(Sv)采用上覆岩体的容重进行估算。 因此按岩石密度(2.65 g/cm3)估算出各测段处的垂直应力值,水压致裂法地应力测试结果见表1。

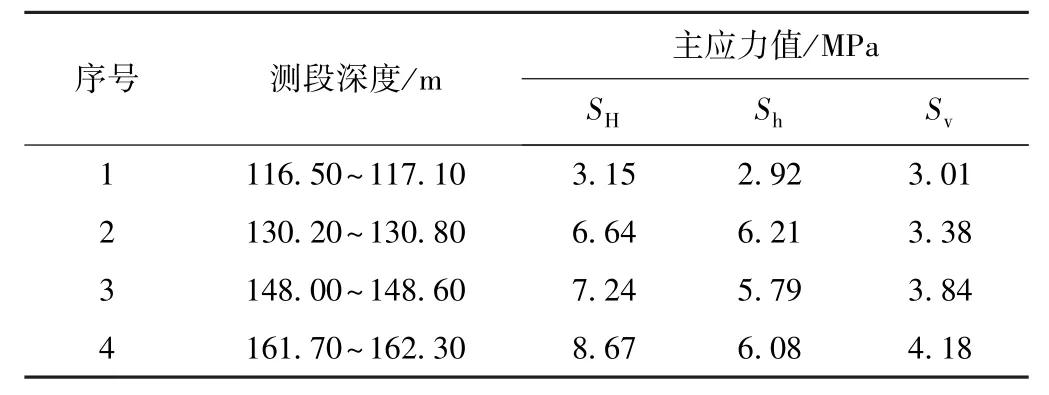
表1 水压致裂法地应力测试结果

3 三维地应力场非线性反演

3.1 基本流程

基于“反演+正算”原理的地应力场非线性反演方法计算步骤如下。

(1)根据地形平面、钻孔剖面等地质资料建立该隧道三维地质力学数值模拟模型。

(2)将应力边界条件作为输入参数,设置不同的应力边界条件参数,采用有限差分法对不同应力边界条件下的数值模型开展岩体地应力计算分析。

(3)提取上述数值模拟结果中地应力测点处的计算值,将边界条件参数作为输入样本、各个测点的地应力计算值作为输出样本,组建训练样本数据库。

(4)利用BP 神经网络的自学习功能,对上述样本进行训练、检验,构建非线性预测模型。

(5)确定隧道模型实际应力边界参数的搜索范围,将输入参数在搜索范围内进行离散化,将每组参数输入到训练好的非线性预测模型中,从而得到对应的地应力预测值。

(6)将地应力实测值作为期望,通过最佳逼近目标函数将地应力计算值与期望值比较,采用遗传算法寻找使目标函数取得最小值的参数组,即参变量全局寻优。

(7)将第(6)步得到的最优参数组输入到隧道数值分析模型中进行“正”算,从而获得地应力场。

3.2 数值模型

采用有限差分软件Flac3D 建立三维数值分析模型。 模型以地应力测孔为中心,沿隧道纵向朝两边延伸5 000 m、垂直隧道两边各延伸3 000 m,竖直向下模拟至高程89 m。 银河山隧道地表地质模型见图3(单元数为52 109,节点数为10 026)。

图3 银河山隧道地表地质模型

银河山隧道区域地质条件复杂,岩体分区、分层较多,地质历史上构造运动较强烈,地表风化、剥蚀等外在地质营力非常明显,岩体应力条件极其复杂。 因此,地应力反演采用弹塑性本构模型进行计算,模拟时相关参数见表2。

表2 岩体力学参数

3.3 地应力反演

数值模型的边界水平投影是规则的长方形,2 组平面分别沿东西向和南北向,恰好与该区域的最大、最小主应力方向平行,模型边界上的剪应力可忽略不计。为简便起见,只在模型的4 个侧面边界上施加法向应力荷载。

设定24 组非线性荷载边界条件模式样本数据(见表3),并利用FLAC3D 软件对每组参数样本进行数值分析。 将其中20 组计算结果用于神经网络训练,剩下的4 组则用于训练效果检验。

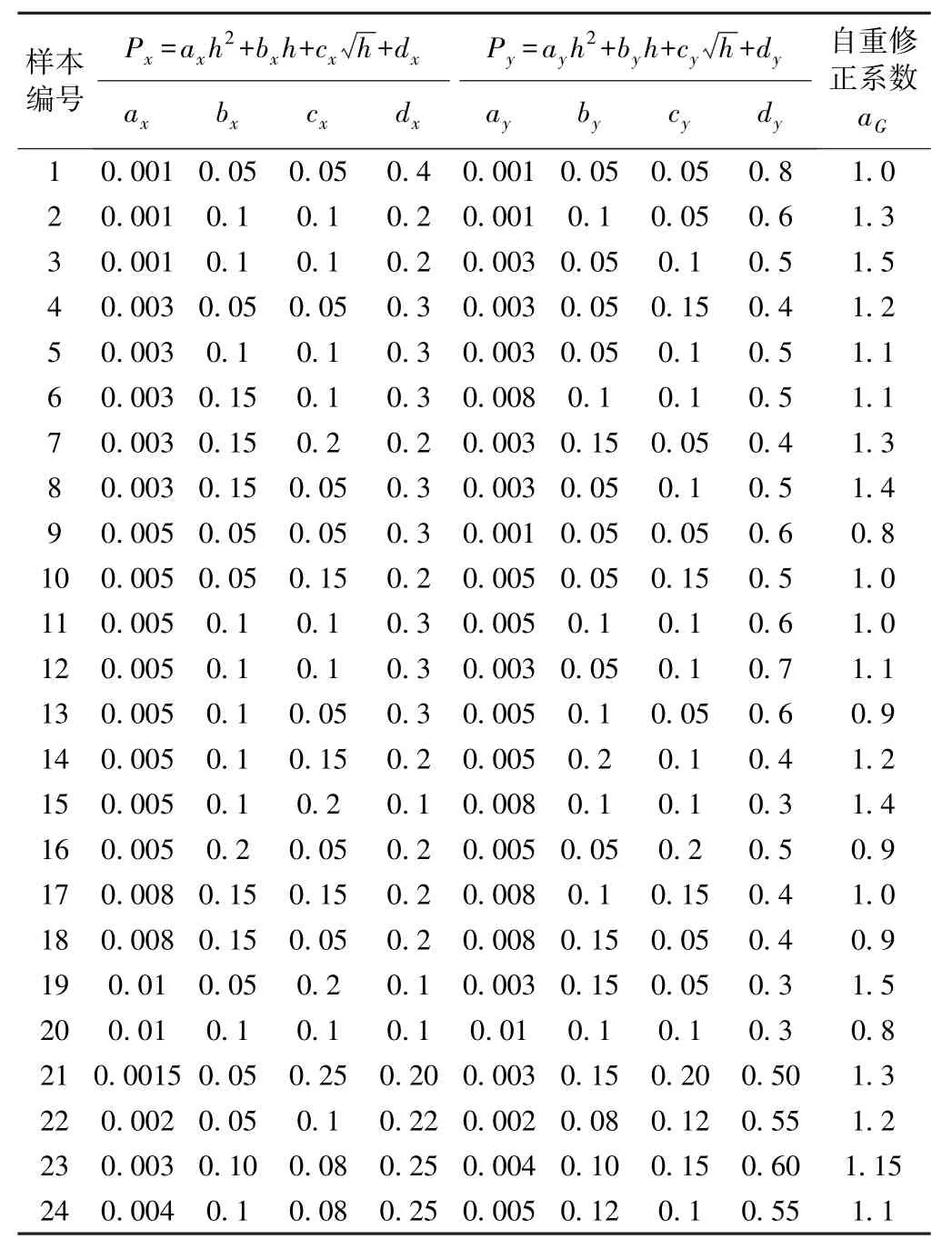
表3 边界条件参数样本数据

样本计算结束后,从上至下选择4 个测点的最大和最小的水平主应力计算值作为学习训练的输出项,而将应力边界参数作为对应输入项。 输入值的格式为aG、ax、bx、cx、dx、ay、by、cy、dy,输入值见表3;输出值的格式为测点1 的SH、测点1 的Sh、测点2 的SH、测点2 的Sh、测点3 的SH、测点3 的Sh、测点4 的SH、测点4 的Sh,输出值见表4。

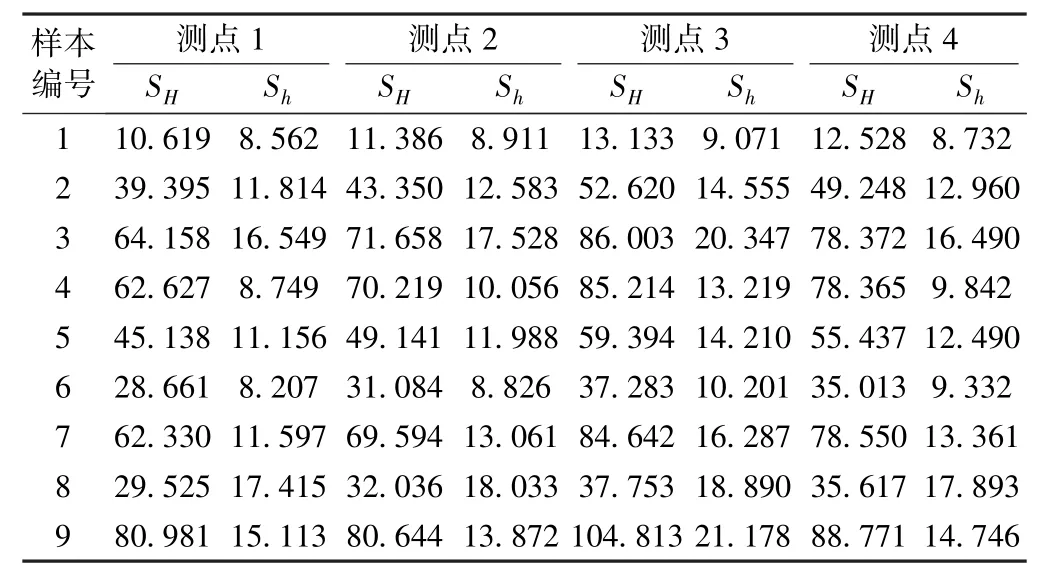
表4 地应力计算值样本数据MPa

把样本数据分为训练数据和检验数据,其中,训练数据为1~ 20 号,检验数据为21~ 24 号。 在正式学习训练前,选定合适的允许误差、学习速率、冲量系数和最大迭代次数等必须参数。 选定后,开展神经网络自学习训练,并对训练效果进行同步检验。 如果效果不理想,则需要对模型进行再次补充训练,直至检验效果达到要求。 4 个检验样本预测值和计算值对比见表5。

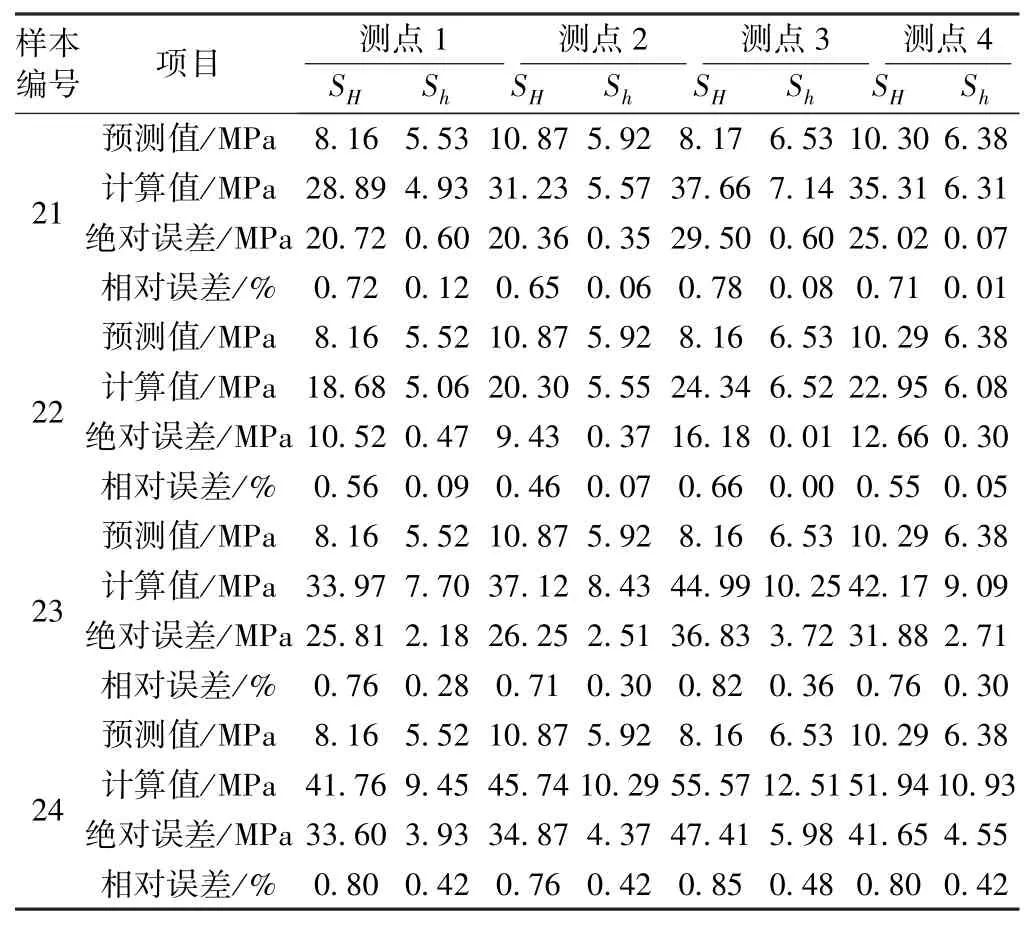
表5 神经网络学习训练检验

根据地应力实测结果,估算出应力边界条件的取值范围,将其作为遗传算法的参数值搜索范围。 应用遗传算法优异的全局寻优能力,在参数值域范围内搜索最逼近地应力实测值的应力边界条件参数组,其结果为aG= 0.813 731,ax= 0.005 402,bx= 0.113 426,cx= 0.056 345,dx= 0.362 836,ay= 0.008 859,by=0.073 725,cy=0.171 401,dy=0.382 576。 将以上参数搜索结果代入表3,并将应力边界计算值施加到数值模型中再次进行数值模拟“正算”,从而获取银河山隧道地应力场的分布结果。 隧道纵剖面的水平最小主应力和最大主应力见图4、图5。

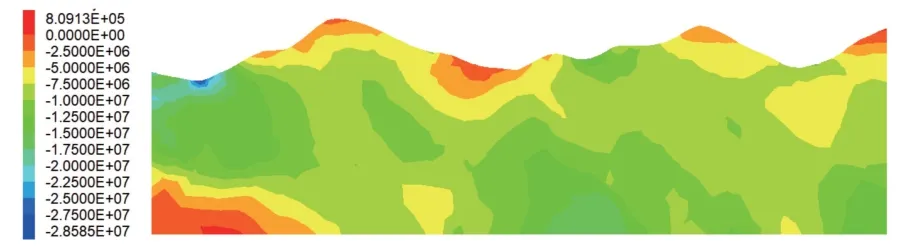
图4 水平最小主应力(单位:Pa)

图5 水平最大主应力(单位:Pa)

最后,将地应力实测值与反演结果进行对比,结果见表6。

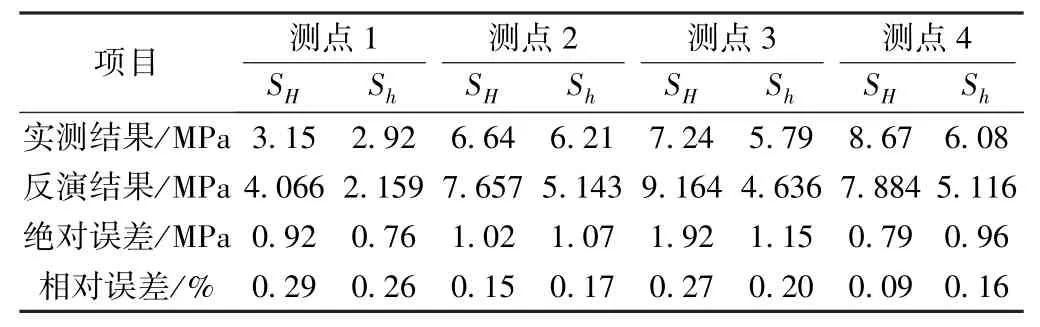
表6 地应力实测值与反演结果的对比

由表6 可知,非线性反演方法得到地应力值与实测值比较接近,最大水平主应力、最小水平主应力的最大相对误差分别是29%和26%,平均偏差分别为20.01%和19.80%。 根据相关经验,地应力现场测试的误差范围一般为20%~ 30%[19-20],由此可知,本次反演结果可靠。

4 对比分析

4.1 荷载工况简化模型

地应力场由自重应力场和构造应力场叠加而成,多元回归分析方法是分别构建自重和构造应力场,然后采用最小二乘法进行回归分析并完成回归显著性检验,之后建立合适的线性应力回归函数,同时将二维应力场扩展至三维应力场。 该方法从局部到整体,能够反映大范围内的地应力场特征,方法简单且应用广泛。

假设岩体中任意观测点的最大和最小水平主应力分别与岩体自重(情况1)、小主应力方向的构造应力(情况2)和大主应力方向的构造应力(情况3)有关,本研究中水平初始边界最大、最小构造应力荷载值分别为8 MPa、6 MPa,见图6[12]。 因此,各个观测点的地应力多元线性回归方程可以表示为

图6 典型荷载工况简化加载模型

式中,^σ为观测点的水平最大主应力或水平最小主应力;σv、σu、σw分别为观测点在工况1、工况2、工况3 下的最大或最小水平主应力计算值;d为误差;a、b、c为待回归系数。

4.2 数值模拟计算

(1)工况1

利用实测的岩体密度、弹性模量和泊松比,计算重力产生的自重应力场。 网格模型中,固定住该模型z向的位移,数值模拟时在模型的底部平面施加法向位移约束(即z方向位移恒为0)。 同时,将垂直于x轴的2 个平面的x轴方向位移设置为0;将垂直于y轴的2 个平面的y方向位移设置为0。

(2)工况2

岩体的力学参数和网格模型同情况1,在工况2 时取重力加速度为0。 固定住该模型z向的位移,数值模拟时把约束加在模型底面;在垂直于x轴的2 个平面施加沿x轴方向位的6 MPa 均匀分布的力;固定垂直于y轴的2 个平面的y方向位移,即令其在平行y轴方向不能移动。

(3)工况3

岩体的力学参数和网格模型同情况1,重力加速度取为0。 边界约束为在垂直于y方向的2 个边界面上施加8 MPa 均匀分布的构造应力;但是,垂直于x方向的2 个边界曲面施加0 位移约束,dx=0,垂直位移约束施加在模型底部,dz=0。

采用弹性本构模型分别对3 种工况进行数值模拟计算,由此得到各种工况4 个观测点的最大、最小计算水平主应力见表7。

表7 不同工况最大、最小水平主应力 MPa

4.3 回归模型参数求解

根据上述计算结果,确定了地应力场多元线性回归超定方程组的系数矩阵。

式中,A为超静定线性方程组的系数矩阵(8×4);L为回归方程的系数矢量(4×1);Sm为现场实测数据矢量(8×1)。 矩阵A及矢量Sm的参数见表8。

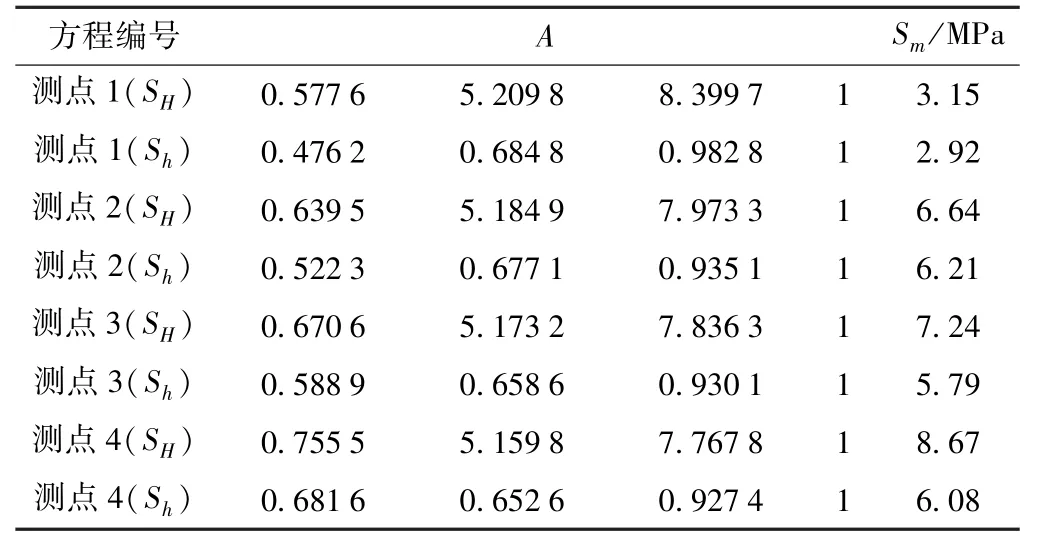
表8 矩阵A 及矢量Sm 相关参数

通过多元回归分析,获得的回归系数分别为a=10.925 0,b=10.372 0,c=-6.611 3,d=-1.688 5,复相关系数为R=0.867 3;表明回归效果显著,回归计算模式合理。 将3 种工况的观测点计算值代入式(1),得到Sm的拟合计算值为[4.124 8,4.119 1,4.361 8,4.858 3,5.486 0,5.427 1,10.727 4,6.395 4]。SH、Sh反演值和实际值对比见图7、图8。

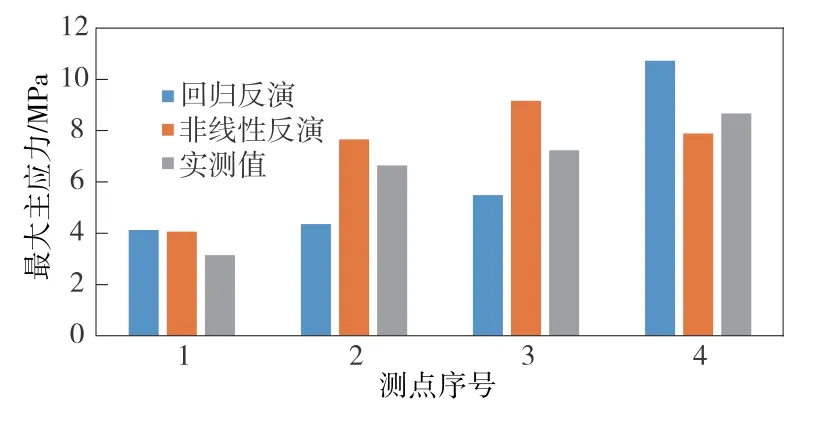
图7 最大水平主应力实测值与非线性反演值、回归分析值对照

图8 最小水平主应力实测值与非线性反演值、回归分析值对照

由图7 可知,针对最大水平主应力,回归分析的结果与实测值的平均偏差为28.3%,非线性反演分析的结果与实测值的平均偏差为20.01%。

由图8 可知,针对最小水平主应力而言,回归分析的结果与实测的平均偏差为21.03%,非线性反演分析的结果与实测值的平均偏差为19.8%。 由此可见,非线性反演方法计算结果优于多元回归分析方法。

5 结论

基于“反演+正算”原理,建立地应力场反演三维数值分析模型,设定多组非线性荷载边界条件模式,通过数值模拟方法获得测点地应力计算值,将边界条件数据和地应力计算值分别作为输入和输出样本,再通过BP 神经网络将样本进行训练,并结合遗传算法寻优功能得到地应力实测数据对应的最优应力边界条件,之后,将该边界条件输入到地应力场反演三维数值分析模型中进行计算,获得该模型三维地应力场。 采用上述方法对某高铁银河山隧道地应力场进行反演,同时与多元回归分析方法的反演结果进行对比验证。结果表明,地应力场具有高度的非线性特征,与多元线性回归分析方法相比,非线性反演方法得到的结果与实测值的平均偏差分别为20.01%(最大水平主应力)、19.80%(最小水平主应力),明显小于多元线性回归分析方法得到的平均偏差。